Dado: 12 moedas, uma delas é falsa, difere apenas em peso. Desconhecido mais leve ou mais pesado. São fornecidas escalas de alavancagem que mostram que a carga de um lado é mais pesada. Para 3 pesagens, você precisa encontrar uma moeda falsa.
Por experiência, aconselho você a não se apressar, a decidir por escrito. O quebra-cabeça “12 moedas, 3 pesagens” surgiu várias vezes na minha vida. A primeira vez que minha amiga me perguntou, ela decidiu depois das Olimpíadas e eu tive que quebrar minha cabeça por algumas horas. E alguns anos depois, isso não me foi dado imediatamente. Se você quiser decidir por si mesmo, faça-o em um pedaço de papel.
Abaixo, será apresentada uma análise e estágios da solução. As etapas serão realizadas de acordo com uma metodologia universal de solução de problemas, aplicável tanto à programação quanto à vida. Com a abordagem, resolver o quebra-cabeça será fácil.
Eu sugiro que você, antes de ler, ofereça uma solução. Você tem uma resposta? Verificado?
Se fosse um software, as perguntas seriam: “Você programou, testou o algoritmo? Você examinou os casos de teste e os verificou?
Como mostra a experiência, para resolver, é necessário desenhar uma árvore de decisão e verificar todos os 12 casos.

1. DicasNo processo de resolução, ajudará:1) Diminuição da entropia (medidas de incerteza) e respostas às perguntas:
- O que você aprendeu na etapa anterior?
- O que reduz a incerteza?
- Que informação temos?
- O que mais você precisa saber?
As perguntas são adequadas para qualquer tarefa, projeto. As respostas a eles ajudam a reduzir o risco de falha no cumprimento de prazos, excedentes orçamentários e recuperação dos superiores.
2) Decomposição. A abordagem do simples ao complexo. Se você preparar uma solução para os casos mais simples, use-os para resolver o problema (dividir e conquistar o algoritmo), será mais fácil do que representar toda a situação em sua cabeça.
Os algoritmos de divisão e conquista dividem uma tarefa em duas ou mais subtarefas do mesmo tipo, mas menores em tarefas elementares, e combinam suas soluções para obter uma resposta para o problema original.Componha perguntas para decomposição. Qual você sugeriria?
2. DecomposiçãoQue perguntas você formulou para a decomposição? Alguma correspondência?
1) Qual é a situação mais elementar? O que podemos fazer em uma pesagem?
Para uma pesagem, podemos determinar qual moeda é mais pesada, se o peso das moedas é igual.
2) Se tivermos 2 moedas e, como você sabe, o falso é mais difícil ou mais leve. Como determinar uma farsa em uma pesagem?
É necessário pesar as moedas e, dependendo da seta da balança, determinar a falsificação.
3) Se tivermos 2 moedas e, não se sabe, a falsificação é mais difícil ou mais fácil, como determinar a falsificação em uma pesagem?
Depois de pesar uma das 2 moedas apresentadas com a terceira, sobre a qual se sabe que é genuína.
4) Se tivermos 3 moedas e, como você sabe, o falso é mais difícil ou mais leve. Como determinar uma farsa em uma pesagem?
É necessário comparar duas dessas moedas, se forem iguais, a terceira moeda é falsa.
5) Se tivermos 3 moedas e, é desconhecido, a falsificação é mais difícil ou mais fácil. É possível determinar uma falsificação em uma pesagem?
Infelizmente não.
6) Se tivermos 4 moedas e o falso desconhecido for mais difícil ou mais leve, podemos determinar o falso em uma pesagem?
Infelizmente não.
7) Se tivermos 4 moedas e, se for desconhecido, a falsificação for mais difícil ou mais leve, quantas pesagens você pode determinar como falsas?
Para duas pesagens.
Em seguida, a partir de casos elementares, coletamos situações de 8, 9, 10, 11 e 12 moedas. Como você vê a solução?
Abaixo está a solução completa.
3. DecisãoPrimeiro passo: divida as moedas em 3 grupos de 4: 1 2 3 4, 5 6 7 8, 9 10 11 12.
Compare os dois primeiros grupos. São possíveis três opções:
- o primeiro grupo é mais pesado;
- o segundo grupo é mais pesado;
- são iguais.

1) Se os grupos forem iguais, a moeda falsa estará no terceiro grupo. É necessário encontrar uma moeda falsa de 4 moedas em duas pesagens.
Divida o terceiro grupo em dois: 9 10 11 12
Compare 9 e 10:
- se forem iguais, a moeda falsa no segundo grupo - compare 9 e 11. Se 9 e 11 forem iguais, então a moeda falsa - 12, se não -11
- se não forem iguais, será falso no primeiro grupo - compare 10 e 12. Se 10 e 12 forem iguais - falso - 9, se não - 10.
Então encontramos uma moeda falsa.
2) Considere o segundo caso. Se o primeiro grupo for mais pesado que o segundo, atribuímos ao primeiro grupo o sinal ">", o segundo grupo o sinal "<", o terceiro grupo - "0".
Dividimos as moedas em grupos 1 9 10 11 e 5 2 3 4, pesados. São possíveis três opções:
- São iguais. A moeda falsificada está entre os números: 6 7 8. Compare 6 e 7, se forem iguais, a falsificação é 8, se 6 for maior, a falsificação - 7, se 7 for maior, a falsificação - 6, pois nesse caso a moeda falsificada é mais fácil.
- O primeiro grupo é mais pesado, então a moeda falsa é 1 ou 5. Compare 1 e 9 se forem iguais - a moeda falsa - 5, se não - 1.
- O primeiro grupo é mais fácil, depois o falso entre as moedas 2 3 4, pois é sabido que 9, 10 e 11 são reais, e o segundo grupo pode ser superado apenas pelas moedas 2, 3 e 4. Compare 2 e 3, se forem iguais, falso 4, se 2 é mais pesado, então falso é 2; caso contrário, o terceiro é falso.
3) O caso em que o segundo grupo é mais pesado que o primeiro é semelhante ao segundo.
O diagrama geral da Árvore de Decisão é apresentado abaixo.
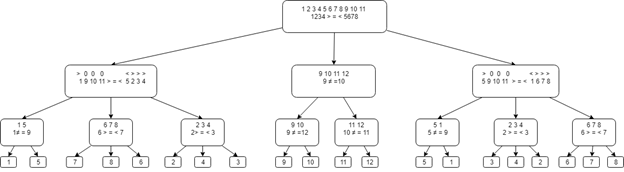
ConclusãoQuando uma tarefa chega para revisão ou depuração, é bom aplicar a abordagem acima:
- Decida o que é dado?
- Quais casos / tarefas elementares podem ser decompostos?
- O que é desconhecido para resolver o problema? Que experimentos precisam ser feitos para reduzir a entropia?
- Corra.
- O problema está resolvido? Não? Volte para a etapa 1.
Soluções de sucesso.