Estimativa do VaR e ConVaR para o preço das ações da empresa cazaque

Nas últimas décadas, a economia mundial cai regularmente nesse turbilhão de crises financeiras que afetaram cada país. Isso quase levou ao colapso do sistema financeiro existente, devido a esse fato, especialistas em modelagem matemática e econômica passaram a usar métodos para controlar as perdas de ativos e portfólio no mundo financeiro (Lechner, LA e Ovaert, TC (2010) Existe uma tendência crescente de modelagem matemática de um processo econômico para prever o comportamento do mercado e uma avaliação de sua sustentabilidade (ibid). Tendo sem a atenção necessária para controlar e avaliar adequadamente as ameaças, todos entendem que é capaz de desencadear um tremendo custo no desenvolvimento da organização ou até falir.

O Valor em Risco (VaR) acabou sendo uma abordagem regular para capturar o risco entre instituições do setor financeiro e seu regulador (Engle, R. e Manganelli S., 2004). O modelo é originalmente aplicado para estimar o valor da perda na carteira de investimentos em um determinado período de tempo, bem como em uma determinada probabilidade de ocorrência. Além do uso do VaR no setor financeiro, existem muitos exemplos de avaliação de valor em risco em diferentes áreas, como a antecipação da equipe médica para desenvolver a gestão de recursos de saúde Zinouri, N. (2016). Apesar de sua primitividade aplicada em um experimento real, o modelo consiste em desvantagens na avaliação (ibid).

O objetivo do relatório é uma descrição do modelo de VaR existente, incluindo uma de suas versões de atualização, a saber, Valor Condicional em Risco (CVaR). Na próxima seção e na seção 3, são explicados o algoritmo de avaliação e o teste do modelo. Para uma ilustração vívida, a perda esperada é estimada no ativo de uma empresa da Cazaquistão que negocia no mercado financeiro de bolsa de valores por um longo período de tempo. As seções finais 4 e 5 discutem e demonstram os resultados do trabalho de pesquisa.

Antecedentes

Acredita-se que o primeiro uso do VaR pelas organizações financeiras gigantes até 40 anos atrás e, conseqüentemente, o VaR tenha se tornado popular entre outras empresas de trading, até mesmo os reguladores financeiros tiveram atenção ao modelo (Linsmeier, TJ e Pearson, ND). 2000). Por exemplo, a Securities and Exchange Commission dos EUA inscreveu o VaR em uma lista de métodos quantitativos para calcular o risco de mercado e propriedades em 1997 (ibid).

Na verdade, de acordo com artigos de Lechner, LA e Ovaert, TC (2010), bem como Linsmeier, TJ e Pearson, ND (2000), o VaR é uma equação de estimativa expressa em unidades monetárias que não excedem a perda na faixa de magnitude durante um determinado período e com um nível de confiança determinado. Normalmente, o nível de confiança da estimativa do modelo (99%, 97,5%, 95%) ou, em outras palavras, a probabilidade de que algum caso desfavorável tenha acontecido e a influência no mercado sejam iguais a 1, 2,5 e 5% (ibid).

A conhecida equação do VaR pode ser descrita (Phelps S, 2018):

$$$(1) \ VaR (X) = \ min \ \ {x \ \ epsilon \ R: 1-F_x (-x) \ geq \ alpha \}$

Onde X é uma variável aleatória que executa a quantidade do valor do portfólio e é uma função de distribuição cumulativa (ibid).

Por outro lado, Hooper GP (1996, citado em Lechner, LA e Ovaert, TC 2010) denota o VaR com confiança que alfa define de uma maneira bastante elementar:

$$$(2) \ VaR ^ \ alpha (X) = \ sigma \ sqrt {\ delta t} N ^ {- 1} \ alpha$

Onde $$$\ sigma$é o desvio padrão dos retornos de ações selecionados, $$$\ delta t$é a raiz quadrada do período de tempo fixo e $$$N ^ {- 1}$é a função de distribuição cumulativa (CDF) para uma distribuição normal (Lechner, LA e Ovaert, TC 2010).

Embora o VaR seja um método conhecido e manipulado para estimar o risco decidido do portfólio, há deficiências em um caso ao medir a vulnerabilidade a problemas de mercado finais, ou seja, o exemplo está relacionado à probabilidade de eventos extremos de mercado não serem adequadamente identificados. da distribuição normal (Capiński, MJ 2015). Para resolver esse problema, foi criado o Valor Condicional em Risco (CVaR), que considera o valor esperado da perda em vez do VaR (ibid). O CVaR define como:

$$$(3) \ CVaR ^ \ alpha (X) = \ frac {1} {\ alpha} \ int ^ \ alpha_0 VaR ^ \ beta (X) d \ beta = \ frac {-1} {\ alpha} q ^ \ beta (X) d \ beta$

$$$(4) \ CVaR ^ \ alpha (X) = - \ frac {1} {\ alpha} (E [X 1 _ {\ {X \ leq q ^ \ alpha (x) \}}] + q ^ \ alpha (X) (\ alpha-P [X \ leq q ^ \ alpha (X)]))$

Onde Ahn D.-H. et.al (1999, citado em Capiński, MJ 2015) interpretam $$$-q ^ \ alpha (X)$
como VaR da variável aleatória X (retorno do preço das ações) com probabilidade $$$\ alpha$e define como o quantil superior de X.

Além disso, Acerbi C. e Tasche D. (2002, citado em Capiński, MJ 2015) confirmam: “O CVaR é uma medida de risco coerente”. Rockafellar, RT e Uryasev, S. (2000) observam que o CVaR possui recursos extras: transição-equivariante, positivamente homogêneo, convexo e etc.

O capítulo seguinte do artigo demonstra a implementação do conhecido Valor em Risco (VaR) e Valor Condicional em Risco (CVaR) também anunciado como Déficit esperado (ES) observado no trabalho de Rockafellar, RT e Uryasev, S. (2000) usando a tecnologia da informação em dados reais.

Metodologia

Vamos considerar os métodos mais usados ​​para calcular o VaR, bem como suas vantagens e desvantagens.

Segundo o relatório de Lechner, LA e Ovaert, TC (2010), a simulação histórica é uma abordagem difundida para avaliar o VaR e sua modificação. Na modelagem histórica dos dados, tomamos os valores das flutuações financeiras do portfólio que já são conhecidas de medições passadas. Portanto, é apenas uma sequência lógica que a desvantagem desse método é a impossibilidade de criar previsões para portfólios sem uma informação sobre ele. O método Monte Carlo é, em muitos aspectos, idêntico ao método de modelagem histórica, usado para a técnica de alta precisão, a principal diferença clara de que o cálculo da simulação de Monte Carlo não é baseado em dados reais, mas realizado em valores gerados aleatoriamente. A vantagem desse método é a possibilidade de considerar como um grande número de situações e emular o comportamento do mercado em condições extremas, além de não haver necessidade de uma aproximação entre fatores de risco e mudanças em um portfólio (Glasserman, P., Heidelberger, P e Shahabuddin, P., 2002). A desvantagem óbvia são os grandes recursos computacionais necessários para implementar essa abordagem (ibid).

Naturalmente, esses não são os únicos métodos para calcular modelos de VaR. Além disso, existem modelos simples lineares e quadráticos de previsão de preços e um método bastante complicado de variações, que não foram abordados no ensaio.

Análise de dados

Como dados secundários para testar a avaliação precisa, é feito o estoque da KAZ Minerals. Para esclarecer o trabalho, o preço fechado ajustado é utilizado para simulação em um modelo. As ações da empresa KAZ Minerals (KAZ.L) são um dos valores mobiliários negociados com sucesso entre empresas do Cazaquistão na Bolsa de Londres (LSE), bem como categorizados na lista Premium Equity Commercial Companies (Bolsa de Londres, 2019). A entidade se apresenta como a enorme empresa de mineração de cobre no Cazaquistão (Kazminerals.com. 2019).

Os dados históricos do preço das ações são baixados do site do Yahoo Finance (Finance.yahoo.com, 2019). Para garantir a validade do trabalho, é observado o período de um ano, de 22 de março de 2018 a 22 de março de 2019. Além disso, para evitar a interrupção das informações, na análise, os dados históricos do preço das ações KAZ.L são baixados no formato Valores Separados por Vírgulas (CSV), devido ao fato de o formato CSV ser compatível com o programa Microsoft Excel (Excel) . Os dados escolhidos do projeto são apresentados como um gráfico de linhas usando o Excel na Figura 1.

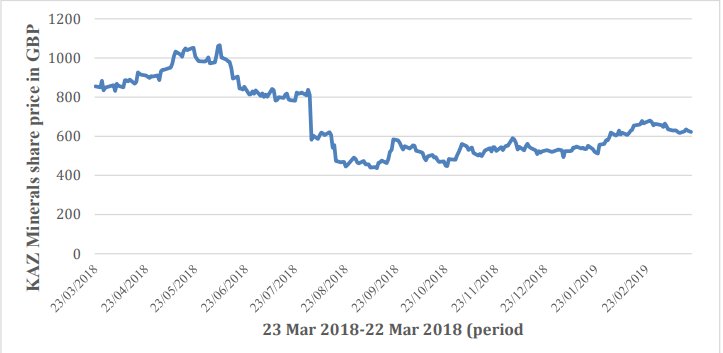
Figura 1. A dinâmica da mudança do preço das ações da KAZ Minerals por um ano

Devido à limitação da linha do tempo do relatório, em vez de usar uma linguagem de programação como Python para implementação de modelos de avaliação, os dados são analisados ​​completamente no Excel.

Constatações

Na seção anterior, os modelos para prever as perdas potenciais em um portfólio com base nas equações VaR e CVaR e usaram alterações no preço das ações da KAZ Minerals de 23 de março de 2018 a 23 de março de 2019, baixadas da fonte oficial da Yahoo Finance (Finance.yahoo). com, 2019). Ambas as equações executadas para cada data do período escolhido.

A Tabela 1 demonstra o retorno médio diário dos negócios, um desvio padrão de retorno, um valor mínimo de retorno e um valor máximo de retorno para este exemplo.

Tabela 1. Compartilhe o retorno médio e o desvio padrão dos retornos

A média correspondente é -0.0006 e o ​​desvio padrão 0,0355 dos retornos para a KAZ Minerals de segurança exclusiva selecionada. Além disso, a variação dos retornos é 0,0013. Além disso, certamente deve ser sublinhado que no trabalho de pesquisa de Vee, DNC e Gonpot, P. N (2014) os retornos das ações do Cazaquistão mostraram um valor significativo em volatilidade, no entanto, a estimativa estava relacionada ao índice da Bolsa de Valores do Cazaquistão na pré e pós-período de 2008. Além disso, deve-se mencionar que o valor máximo entre retornos é 0,0998, bem como o valor mínimo entre retornos é -0,2829 na distribuição de perdas. A Tabela 2 apresenta os valores máximos e mínimos entre o preço das ações fechadas ajustadas (KAZ.L) nas negociações de libra esterlina (GBP) na Bolsa de Londres de 23 de março de 2018 a 22 de março de 2019.

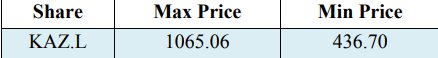
Tabela 2. Preço máximo e mínimo das ações KAZ Minerals em GBP

A etapa a seguir é avaliar o valor em risco (VaR) e o valor condicional em risco (CVaR) para o nível de confiança - 0,99, 0,972 e 0,95. Os valores são revelados na Tabela 3.

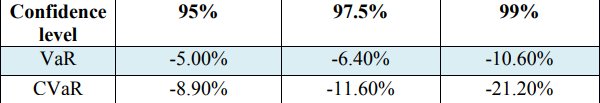
Tabela 3. Valores de VaR e CVaR dos retornos

O tamanho da amostra da simulação é obtido em 252 unidades de 23 de março de 2018 a 22 de março de 2019 durante um ano.

Discussão

No relatório, as equações de VaR e CVaR demonstram o valor credível no caso dos modelos de estimativa para um preço das ações da empresa cazaque no período de curto prazo. Com esses valores, por um lado, ambos os métodos apresentam resultados adequados para avaliar o valor das ameaças ao portfólio de investimentos (Linsmeier, TJ e Pearson, ND 2000; Lechner, LA e Ovaert, TC 2010).

Além disso, de acordo com as conclusões da Tabela 2, o próximo aviso é direto que os valores para o CVaR são mais massivos em comparação com os valores do VaR em todas as medidas de nível de confiança. Pode-se dar uma explicação pelo fato de o CVaR assumir o risco médio escolhido da carteira, consequentemente, é mais sensível na cauda da distribuição de perdas do que o VaR. Isso prova mais uma vez que o CVaR é um risco coerente (Acerbi C. e Tasche D., 2002, citado em Capiński, MJ 2015; Rockafellar, RT e Uryasev, S. 2000). Por exemplo, no que diz respeito à adequação de ambos os modelos de estimativa, com nível de confiança 99% VaR e CVaR ilustram o percentual significativo de perda de retorno das ações. Para ser mais preciso, pode ser detectado um VaR de -10,60% e um CVaR de -21,20%. É bastante claro o motivo das medidas colossais do CVaR com um determinado nível de confiança de 99%, devido ao fato da faixa de preço das ações durante o período, o preço máximo ser 1065,06 GBP. O preço mínimo das ações é 436,70 GBP, respectivamente.

Conclusão

Tendo considerado tudo acima, deve-se obviamente mencionar novamente que o objetivo do relatório é demonstrar a estimativa do valor de uma possível perda para a empresa cazaque (KAZ Minerals) durante um período de 23 de março de 2018 a 22 de março de 2019. formado nas equações Valor em Risco (VaR) e Valor Condicional em Risco (CVaR). Os desempenhos da simulação são comparados entre si no mesmo período de tempo. Os resultados mostram o valor significativo de cada método e comprovam o trabalho anterior na mesma área em que o CVaR possui medidas mais precisas em comparação com o VaR (Acerbi C. e Tasche D., 2002, citado em Capiński, MJ 2015; Rockafellar, RT, e Uryasev, S.2000).

Apesar das críticas, o VaR é uma ferramenta difundida em todas as instituições financeiras até os dias atuais e existe uma ampla gama de sua versão de modificação. Devido aos obstáculos do cálculo complexo na pesquisa aprofundada, o experimento é realizado usando o Microsoft Excel em vez de usar uma linguagem de programação como Python, assim como os resultados são revelados no relatório. Os resultados do ensaio podem servir de base para trabalhos posteriores no uso de medidas complexas de avaliação de risco para o portfólio no setor de bolsas de valores, no setor de seguros e no setor de investimentos.