A seguir, diremos algumas palavras sobre a alternativa de tempo discreto aos modelos matemáticos na forma de equações diferenciais lineares, que geralmente é conhecida, mas bastante inesperada para os engenheiros, a saber, modelos autorregressivos - média móvel e perspectivas muito incomuns para essa modelagem, cujas capacidades excedem significativamente o que você está acostumado a obter do LDU.
A lista de recursos potenciais da tecnologia inclui análise de sistemas com uma perturbação recebida inacessível para observação, determinação das propriedades de ressonância de tais sistemas, espectro e processo de excitação externa, estimativa espectral de processos por suas curtas realizações, modelagem do comportamento de sistemas com baixa frequência de amostragem ao longo do tempo, etc.

Os processos ARMA, bem conhecidos pelos economistas (mais precisamente, os "econométricos"), são muito menos conhecidos pelos especialistas em regulação automática e, na minha opinião, dificilmente são usados por engenheiros mecânicos e engenheiros radioeletrônicos, especialmente os da "velha escola". O artigo tenta indicar algumas possíveis áreas de aplicação da teoria ARMA na prática de engenharia.
Em poucas palavras, simplificado, para quem não conhece o assunto, sobre o qual, de fato, é. O processo estocástico de tempo contínuo x (t) por razões óbvias "digitais" na prática geralmente combina a sequência de tempo discreto x [i] com o intervalo de amostragem Δt.
Em princípio, para qualquer processo x [i] é possível uma representação do formulário
x [i] - a 1 · x [i-1] - a 2 · x [i-2] - ... - a p · x [ip] = b 0 · f [i] + b 1 · f [i- 1] + ... + b q · f [iq] (1),
onde
ak e
k são coeficientes constantes (para este modelo), chamados de modelo de média móvel de regressão automática com a ordem de regressão automática p e a média móvel q. ou um modelo ARMA (p, q), f [i] é uma espécie de processo "de entrada", sobre o qual um pouco menor. Muitas vezes (1) é escrito em uma forma ligeiramente diferente (6).
Basicamente, é apenas um filtro digital que possui peças AR recursivas e MA não recursivas.
Existe uma correspondência entre os modelos ARMA (p, q) e sistemas lineares (por exemplo, mecânicos), por exemplo, descritos pela conhecida equação diferencial linear da forma
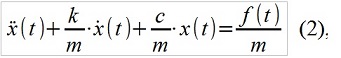
onde m, c, k é a massa, rigidez e amortecimento do sistema mecânico, f (t) é a força externa. A contraparte ARMA é assim:
x [i] - a 1 · x [i-1] - a 2 · x [i-2] = b 1 · f [i-1] (3),
os coeficientes do modelo podem ser facilmente encontrados através dos valores próprios λ
1 e λ
1 * (por questões de brevidade, o caso "oscilante" é considerado) do sistema linear e Δt:
a
1 = z + z *, a
2 = - z · z *, b
1 = j (z * -z) · Δt / (2mω
1 ),
onde z = exp (λ
1 · Δt), λ
1 = -ε
1 + jω
1 , j é a unidade imaginária, * é a conjugação complexa
para referência:

Para o sistema de teste, m = 1 kg, c = 100 N / m, k = 0,75 kg / s, Δt = 0,12 s.,
modelo ARMA (2,1) obtido
x [i] - 0,69433x [i-1] +0,91393 x [i-2] = 0,010696f [i-1](Uma breve explicação de como (3) é geralmente obtida de (2). A função de transição de pulso do nosso sistema linear, isto é, a resposta do sistema a um único pulso:
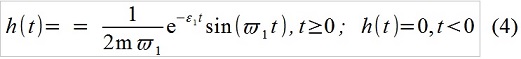
O registro (2) na forma “integral” é chamado de “convolução” f (t) eh (t), significando que envolve considerar a ação externa como uma sequência de impulsos elementares. Em tempo discreto, escreva, assim, por exemplo, assim:
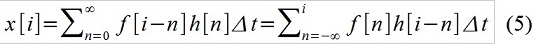
Ao adicionar x [i], x [i-1] e x [i-2] usando os fatores selecionados 1, a
1 e a
2, eles atingem a aniquilação mútua das infinitas “caudas” h [i] - f [i] permanece no lado direito · H [0] = f [i] · 0 ef [i-1] · h [1] = f [i-1] · b
1 . Do ponto de vista da teoria ARMA, o modelo de dimensão infinita da média móvel MA (∞) é transformado em ARMA (2,1) (embora alguns digam que um modelo puramente autoregressivo AR (2) = ARMA (2,0) foi obtido por acidente.
Observação 1. Um leitor familiarizado com o processamento digital de processos dirá que apenas discretizar h (t) não é muito correto - é necessário limitar a função h (t) por frequência a 1 / (2Δt) (filtro). Caso contrário, há um erro de mascaramento de frequência. Os gráficos da resposta em frequência e resposta em fase do nosso sistema, os modelos “analítico” e ARMA, mostram por que esse erro na maioria dos casos de engenharia pode ser negligenciado (Fig. 1) (aqui, a resposta em frequência é em escala logarítmica).
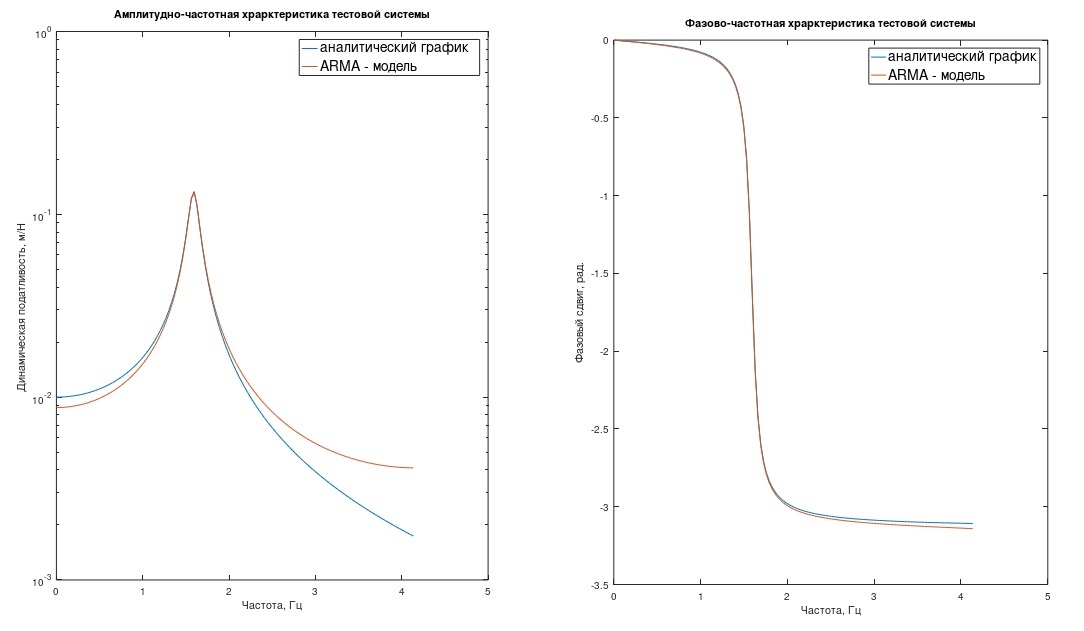
Fig. 1 Resposta de frequência e resposta de fase do sistema de teste.
Observação 2. Na prática, a ordem do modelo ARMA pode ser significativamente maior que o exemplo considerado acima, devido, por exemplo, a vários graus de liberdade de um sistema mecânico ou a um espectro complexo de influência externa real.
Observação 3. Muito importante. Existem métodos (não considerados aqui - muitos mais artigos podem ser escritos sobre eles) que permitem estimar os parâmetros do modelo ARMA (ou seja, a ordem do modelo peq e os coeficientes
ak ebk ) somente pelo processo resultante x [i], sob a suposição que f [i] é um ruído branco hipotético cuja variação também pode ser estimada. Em geral, essa avaliação é a parte principal de toda a teoria ARMA. Embora esses métodos não diferam em particular a perfeição, eles são de considerável interesse.
Agora, por que, de fato, tudo isso pode (ou poderia) ser aplicado na prática. Além do bastante óbvio - a rápida construção de sinusoides "manualmente" amortecidos (e não atenuados) a partir dos dois primeiros pontos e dois coeficientes a
1 e a
2 , existem, na minha opinião, aplicações mais sérias desses modelos na prática de engenharia.
1. Bem, na verdade, para a simulação da operação do sistema - damos um sinal externo real f [i] à entrada, obtemos x [i] na saída:
x [i] = a 1 · x [i-1] + a 2 · x [i-2] + ... + a p · x [ip] + b 0 · f [i] + b 1 · f [i- 1] + ... + b q · f [iq] (6)
O modelo ARMA lida com a tarefa melhor do que o modelo de diferenças finitas, no entanto, isso é perceptível apenas em grandes intervalos de amostragem Δt. (na Fig. 2, Δt = 0,12 s (esquerda) e 0,03 s). Em que casos faz sentido mexer com o ARMA - você decide.
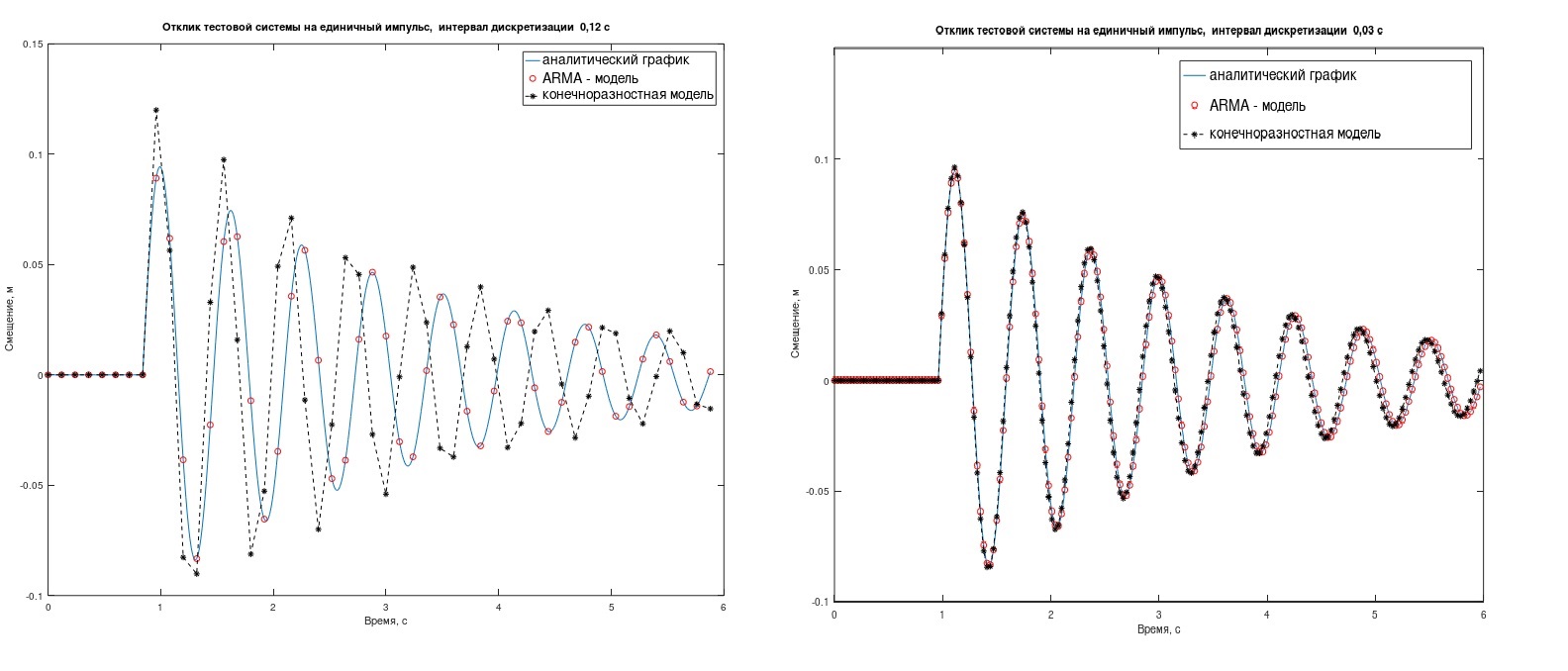
fig. 2. A resposta dos sistemas de teste a um único impulso.
2. Para estimativa espectral, especialmente quando a duração da implementação do processo estacionário é insuficiente para observação. Talvez esta seja a aplicação de engenharia mais famosa dos modelos ARMA. Como um determinado filtro digital e a variação do ruído branco que entra nele serão obtidos para o processo em estudo, a tarefa de construir uma estimativa do PSD é resolvida de maneira óbvia. De fato, é possível obter gráficos SPM externamente muito "suaves" e, ao mesmo tempo, criar a impressão de alta resolução. A melhoria esperada na avaliação está associada ao fato de o pesquisador trazer informações externas sobre a natureza do processo para a construção da avaliação - geralmente definindo uma ordem de modelo conhecida.
Em resumo, você precisa saber com que aparência esse PSD deve parecer. Os estudos “exploratórios” dessa implementação usando métodos clássicos podem fazer pouco, principalmente referindo-se a estudos clássicos (baseados na FFT) de natureza semelhante, mas realizações significativamente mais longas. Há uma chance de erros grosseiros.
3. Para a análise das propriedades de ressonância do sistema e o espectro da ação externa, no caso em que o verdadeiro efeito externo não está disponível para observação. Como já foi observado, é possível, conhecendo o processo x [i], determinar todos os coeficientes do modelo a
k eb (e a variação do ruído branco recebido). Utilizando-os, determinando as raízes de dois polinômios com os coeficientes correspondentes, é fácil encontrar p “polos” e q “zeros” do modelo (λ
k e μ
k ) e construir sua função de transferência - você provavelmente nem pode usar a forma ARMA (aqui dado), e na forma “analítica” usual - como descobrimos acima (Fig. 1), a diferença é pequena. Por exemplo, para p = 5, q = 3 (enquanto abstrai das restrições existentes, aparentemente, na razão de p e q), como opção, temos:
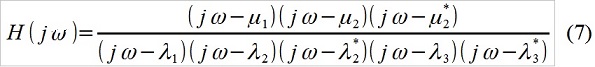
Tudo é muito, muito simplificado, é claro. Com base na natureza conhecida do objeto em estudo (por exemplo, testes de polígono da suavidade de condução do carro) e impacto externo (microprofile da estrada), o pesquisador decidiu reescrever a função de transferência, por exemplo:
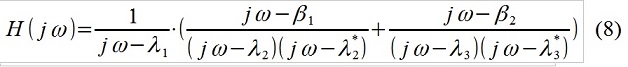
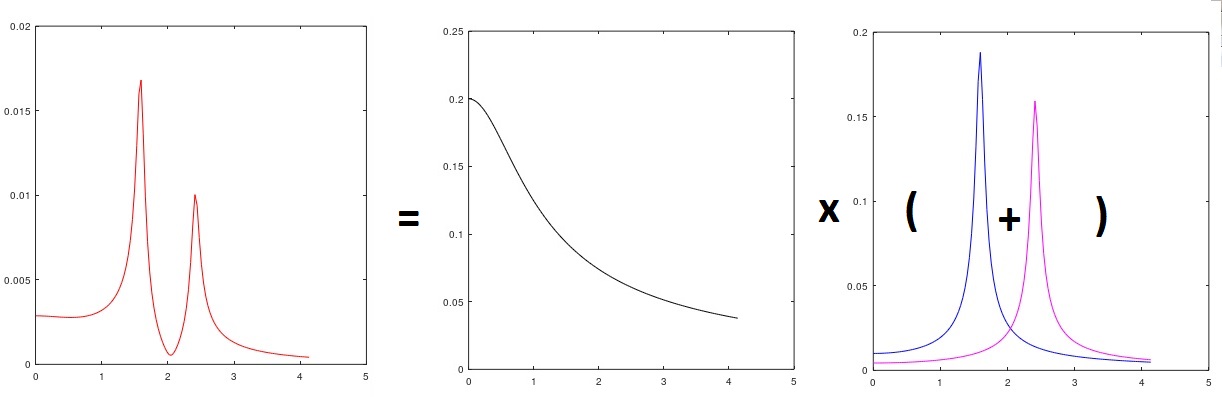
Fig. 3 Análise do espectro do sinal com a alocação da perturbação recebida
e comentado - a parte do modelo associado a λ
1 é obviamente (até quadratura e multiplicação pela variação do ruído branco hipotético de entrada) o microprofile "rosa" da estrada (Fig. 3) (ou seja, identificamos um espectro desconhecido de o sinal de entrada - selecionado manualmente - parece “similar”), λ
2 e λ
3 são as propriedades ressonantes do corpo na suspensão (possivelmente modos de vibração longitudinal-angular e vertical). O principal problema, é claro, estará na determinação dos parâmetros do modelo ARMA. Pelo que acabamos de descrever, você pode, às vezes, sem qualquer ARMA, "rastrear" à moda antiga (embora em formato eletrônico), de acordo com o gráfico de densidade espectral, e medir larguras de pico no nível de -3 dB, etc., ou aplicar curvatura, às vezes mesmo com grande sucesso .
3. Para previsão linear x [i]. Aparentemente, a principal aplicação do ARMA é para economistas. Pode-se observar em (6) que se os coeficientes do modelo foram estimados usando os métodos descritos acima, o próximo valor x [i] pode ser estimado com precisão para um ruído branco hipotético inacessível à observação b
0 · f [i], a variação desse ruído branco é estimada juntamente com os coeficientes do modelo. Normalmente, neste caso, o ajuste dinâmico (em tempo real) dos parâmetros do modelo está implícito. Aparentemente, pode ser útil em sistemas de vibração ativa e redução de ruído. Os especialistas da TAP sabem melhor.
4. Restaurar um processo inacessível que não pode ser observado. Ao dividir o modelo em partes, como mostrado acima na Seção 3, com base no conhecimento sobre a natureza do processo em estudo, é possível avaliar separadamente o espectro da perturbação recebida e, separadamente, as propriedades oscilatórias do sistema físico (separar o modelo em partes). Você pode ir além - criar um filtro (modelo ARMA, o inverso do modelo original) que conecte a saída do sistema à entrada e, com a ajuda do processo resultante x [i], obtenha uma implementação temporária da perturbação recebida. Por exemplo, tente restaurar um sinal não distorcido gravado com distorções lineares precisamente desconhecidas pelo equipamento que não está disponível para um estudo separado (por exemplo, obtido por telemetria).
Com base no meu humilde conhecimento, como resultado, expressarei um julgamento tão subjetivo. A aplicabilidade das tecnologias ARMA aos problemas de engenharia depende muito da perfeição dos métodos para estimar os parâmetros desses modelos a partir do sinal resultante, ou melhor, na minha opinião, é fortemente restringida pela imperfeição desses métodos. O acúmulo de experiência na aplicação do ARMA na engenharia parece fazer sentido, principalmente, em antecipação a um provável "avanço" nessa área.