Prefácio

Acho que precisamos explicar brevemente por que de repente um tópico aparentemente tão trivial com o cálculo do orçamento de energia e por que exatamente os satélites CubeSat? Bem, tudo é bem simples aqui: minha prática curta de ensino mostrou (para mim) que esse tópico, embora básico, estava longe de ser compreendido por todos na primeira vez e, além disso, tinha várias perguntas que não eram óbvias na primeira leitura. Além disso, parece que em coisas tão básicas eles ainda publicam artigos no IEEE e isso está longe de ser feito pelos estudantes . Por que exatamente o CubeSat? Ainda é mais simples aqui: o formato de satélite é interessante (o próprio fato da existência de micro e nanosatélites, como se viu, mergulha muitos em um estado de choque curto) e, portanto, é muito adequado para fins educacionais.

A simulação será realizada no python 3 pelos mesmos motivos que expressei na minha publicação anterior . Vamos considerar o caso de baixa órbita (LEO - Low Earth Orbit) e calcular, de fato, a relação sinal / ruído (SNR - relação sinal / ruído) na entrada do receptor por meio de um downlink (DL - Down Link). Usaremos vários diretórios de acesso aberto e criaremos gráficos para maior clareza.

Todos os códigos-fonte estão disponíveis no meu repositório GitHub . Convido todos os interessados a lê-lo! Ficarei muito grato pela revisão do código e pelas críticas construtivas!

Vamos lá!

Que fórmulas vamos calcular?

Em primeiro lugar, é claro, esta é uma fórmula bem conhecida para a relação sinal-ruído em uma escala logarítmica (em decibéis, simplesmente) para todos (envolvidos no assunto), onde levamos em consideração todas as perdas e amplificações possíveis com uma certa quantidade de abstração:

$SNR = P_t + G_t + G_r + \ eta_ {t} + \ eta_ {r} - L_r - L_t - L - L_ {add} - N [dB] \ qquad (1)$

onde - potência total do ruído térmico (tem uma relação conhecida com a densidade espectral do ruído $N_0 = kT_ {ruído}$ ) em dBm (decibéis por miliwatt), P_t - potência transmitida em dBm, G_t e G_r - ganho da antena no lado do transmissor e receptor, respectivamente (em dBi - decibéis isotrópicos), $\ eta_ {t}$ e $\ eta_ {r}$ - ganho do transmissor e do alimentador receptor (em dB), L_t e L_r - perdas em alimentadores (em dB), perdas no caminho de propagação da onda eletromagnética em dB, $L_ {add}$ - perdas adicionais (por assim dizer, alguma margem) em dB.

Em geral, com os sete primeiros termos, é mais ou menos claro: esses são dados de referência. As coisas são mais interessantes com os três últimos participantes do processo.

Potência de ruído térmico

Como você sabe, não há onde se esconder desse flagelo de dispositivos eletrônicos, você só pode levar em consideração:

$N = 10lg \ left (\ frac {kT_ {noise} B_ {noise}} {10 ^ {- 3}} \ right) [dBm] \ qquad (2)$

onde - constante de Boltzmann $T_ {ruído} = T_a + T_e$ - temperatura sonora equivalente, T_a - a soma das perdas da antena e do ruído (fundo) do céu, $T_e = T_0 (F_ {sys} -1)$ - temperatura do ruído do receptor ( T_0 = 290K e $F_ {sys} = 10 ^ {\ frac {NF} {10}}$ - valor do ruído, calculável a partir da imagem do ruído ( - figura de ruído) da antena receptora), e $B_ {ruído}$ - a largura da banda de frequência do ruído. Você pode usar a banda de ruído igual à largura de banda do próprio receptor no entanto, de acordo com [1, p. 98] a largura de banda do ruído $B_ {ruído}$ pode ser classificado com um pouco mais de precisão $\ gama B$ onde $\ gama$ - constante de 1,002 a 1,57 (refere-se à configuração do receptor).

Perdas adicionais

Aqui você pode pegar algum tipo de suprimento garantido, coletado, via de regra, nos mesmos diretórios ou ir mais fundo e calcular tudo sozinho.

Nesta seção, confio quase inteiramente no bom e velho livro de Cantor, ou seja, nesta parte dele [1, p. 88-96]. Se os leitores tiverem fontes oficiais mais relevantes - compartilhe, acho que será útil para todos.

No que prestamos atenção principalmente:

Perda devido à refração e imprecisão do apontamento da antena ( perda do feixe da antena )

São designados como $L_b = 10log_ {10} (1+ (2 \ theta / \ theta_ {0,5}) ^ 2)$ onde $\ theta$ - largura do feixe e $\ theta_ {0,5}$ - a largura do feixe de meia potência e depende, não importa quão difícil de adivinhar, das características de determinados dispositivos de antena:

Efeitos da fase atmosférica

Se você acredita nos clássicos, essas perdas afetam principalmente a taxa de transferência de dados devido à largura de banda do receptor, porque é desejável selecionar a banda de acordo com a tabela 1 [1, p. 91] Para evitar distorção de fase.

Tab. 1. Largura de banda máxima do receptor para diferentes faixas.

Frequência da portadora, GHz	0,5	1	5	10
Largura de banda do receptor (B), MHz	10	25	270	750

No entanto, deve-se notar que os números são muito impressionantes e, geralmente, não são considerados devido ao ruído térmico.

Perda devido a incompatibilidade de polarização da antena

Pode ser estimado dependendo dos coeficientes de elipticidade $e_1$ e $e_2$ (Estou anexando um recorte do livro soviético como na Figura 1).

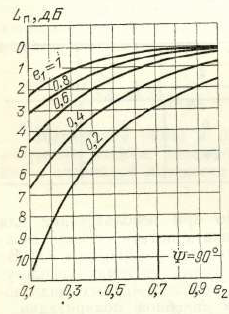
Fig. 1. Dependência de perdas devido à incompatibilidade de polarização entre antenas transmissoras e receptoras de elipticidade. [1, p. 93]

No entanto, me deparei com esse parâmetro como referência. Por exemplo, no cálculo do orçamento de energia para o NanoCom AX100, a perda de polarização é de 3 dB (a perda atmosférica é de 2,1 dB, a perda ionosférica é de 0,4 dB).

Atenuação atmosférica

Podemos avaliar esse parâmetro interessante de acordo com as recomendações da ITU ou calculá-lo nós mesmos. Felizmente, existem bibliotecas especiais como esta .

Atenuação ao longo do caminho de propagação de ondas eletromagnéticas (perda de caminho)

Sem mais delongas, aplicamos a fórmula de Friis para começar :

$L = 20lg \ frac {\ lambda} {4 \ pi d} [dB] \ qquad (3)$

onde $\ lambda$ - comprimento de onda eletromagnético (refere-se de maneira conhecida à freqüência portadora $f_0 = \ frac {c} {\ lambda}$ , É a velocidade da onda eletromagnética (a velocidade da luz, se mais simples)) e - a distância entre os satélites e a estação terrestre.

E aqui chegamos, talvez, à pergunta mais interessante: que distância devemos tomar para os cálculos? Como já mencionado na introdução, estamos considerando os satélites LEO, o que significa que nosso suposto satélite está se movendo em relação à Terra (em contraste com o caso geoestacionário, no qual o satélite, por assim dizer, fica suspenso sobre um ponto).

Obviamente, você pode simplificar tudo o mais possível, tomando o esquema como base (Fig. 2), quando se assume que a órbita do satélite de comunicação está, grosso modo, "acima da cabeça" da nossa estação terrestre.

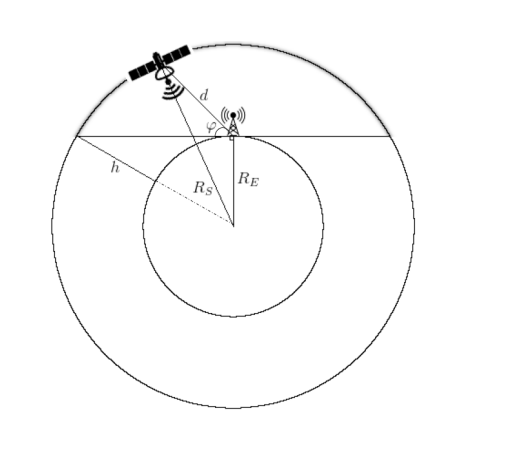
Fig. 2. Descrição esquemática da trajetória CubeSat em baixa órbita terrestre [2].

Então a distância pode ser calculada pela fórmula:

$d = \ sqrt {(R_E + h) ^ 2-R_E ^ 2cos ^ 2 \ phi} - R_Esin \ phi \ qquad (4)$

onde R_E - existe, de fato, o raio da Terra, - altura da órbita do satélite, e $\ phi$ - ângulo de elevação.

No entanto, você pode acelerar um pouco mais, voltar ao clássico (já diferente) [3, p.110-123] e calcular tudo o que já é relativo às coordenadas geográficas reais da estação terrestre (
$lat_ {gs}$ e $long_ {gs}$ ) e a posição real do satélite (nó ascendente instantâneo - $L_ {nó}$ e pólo de órbita - pólo de órbita instantâneo ) Prepare-se, haverá muita trigonometria:

$d_ {min} = R_E \ frac {\ sin \ lambda_ {min}} {\ sin \ eta_ {min}} \ qquad (5)$

onde $\ sin \ lambda_ {min} = \ sin (90 ^ 0 - i) \ sin (lat_ {gs}) + \ cos (90 ^ 0 - i) \ cos (lat_ {gs}) \ cos (long_ {gs} - (L_ {nó} - 90 ^ 0))$ - ângulo central mínimo da Terra, $\ eta_ {min} = arctan \ frac {\ sin \ rho \ sin \ lambda_ {min}} {1 - \ sin \ rho \ cos \ lambda_ {min}}$ - ângulo mínimo do nadir, $\ rho = arcsin \ frac {R_E} {R_E + h}$ É o raio angular da Terra. A distância máxima pode ser calculada por:

$d_ {max} = R_E \ frac {\ sin \ lambda_ {max}} {\ sin \ eta_ {max}} \ qquad (6)$

onde $\ sin \ eta_ {max} = \ sin \ rho \ cos \ epsilon_ {min}$ e $\ lambda_ {max} = 90 ^ 0 - \ epsilon_ {min} - \ eta_ {max}$ ( $\ epsilon_ {min}$ - ângulo mínimo de elevação do satélite).

Para resumir um breve resumo dos parâmetros :

O que escolhemos como pontos de partida : frequência da portadora, altitude da órbita (talvez a posição do satélite e as coordenadas geográficas da estação terrestre - depende da precisão que queremos obter);
Encontramos parâmetros dependentes e ajustáveis do equipamento : potência transmitida, largura de banda do receptor;
Encontramos dados de referência : ganho e perda de antena, ganho e perda do alimentador, temperatura do ruído, perda adicional.

Simulamos o que aconteceu como resultado

Como fonte de parâmetros técnicos para avaliação de downlink, temos exemplos reais de transceptores e antenas para satélites CubeSat, como o NanoCom AX100 e o NanoCom ANT430 . Para uma largura de banda maior, é melhor, é claro, considerar a banda S. A antena de patch NanoCom ANT2000 e o transceptor NanoCom SR2000 estão disponíveis para esse intervalo.

Começamos a verificar o que aconteceu.

from SmallSatLB import * import pandas as pd

Toda lógica é dividida condicionalmente em duas opções: 'rascunho' , em que a fórmula (4) é usada para calcular a distância; e 'preciso' , no qual as fórmulas (5) e (6) são usadas.

'rascunho'

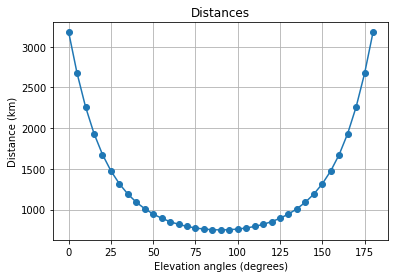
 l_d = LinkBudget(750*1e3, 'draft') #   (   ) d = l_d.distance() #   phi = np.pi*np.array(range(0,181,5))/180 #     plt.plot(180*phi/np.pi, d*1e-3, '-o') plt.title('Distances') plt.xlabel('Elevation angles (degrees)') plt.ylabel('Distance (km)') plt.grid()

 snr, EIRP = l_d.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) #  SNR plt.title('Expected SNRs') plt.xlabel('Elevation angles (degrees)') plt.ylabel('SNR (dB)') plt.legend() plt.grid()

Beleza!

'preciso'

 l_p = LinkBudget(750*1e3, 'precise',\ L_node = 100+90, incl = 90 - 61.5,\ lat_gs = 22, long_gs = 200, eps_min = 5) snr, EIRP = l_p.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) print(min(snr)) print(max(snr))

 >>> 5.556823874020452 >>> 8.667000351847676

Em geral, aqui: temos uma pequena ferramenta para "estimativas" primárias e cálculos de quanto o sinal enfraquecerá, enquanto vai do satélite para a Terra (ou vice-versa).
Obrigado a todos pela atenção!

Lista de literatura usada :

Kantor L. Ya., Askinazi G.B. Comunicações e radiodifusão por satélite: um livro de referência . - Rádio e comunicações, 1988.
Otilia Popescuy, Jason S. Harrisz e Dimitrie C. Popescuz, projetando o subsistema de comunicação para missões de cubos nanossatélites sat: perspectivas operacionais e de implementação, 2016, IEEE
Wertz JR, Análise e Projeto de Missão Espacial Larson WJ, Biblioteca de Tecnologia Espacial. - Microcosm Press e Kluwer Academic Publishers, El Segundo, CA, EUA, 1999.

Calculamos o orçamento de energia de uma linha de rádio para um satélite no formato CubeSat