Termodinâmica de buracos negros

Feliz Dia da Cosmonáutica! Entregamos à gráfica um "livrinho sobre buracos negros" . Foi nos dias de hoje que os astrofísicos mostraram ao mundo inteiro como os buracos negros se parecem. Coincidência? Não pensamos;) Então espere, em breve um livro incrível aparecerá, escrito por Stephen Gabser e Frans Pretorius, traduzido pelo maravilhoso astrônomo do Pulkovo, também conhecido como Astroded Kirill Maslennikov, o lendário Vladimir Surdin fez a edição científica e a Trajectory Foundation apoiou sua publicação.

Trecho "Termodinâmica dos buracos negros" sob o corte.

Até agora, consideramos os buracos negros como objetos astrofísicos que se formaram durante explosões de supernovas ou estão no centro das galáxias. Nós os observamos indiretamente, medindo as acelerações das estrelas próximas a eles. O famoso registro de ondas gravitacionais pelo receptor LIGO em 14 de setembro de 2015 se tornou um exemplo de observações mais diretas de colisões de buracos negros. As ferramentas matemáticas que usamos para entender melhor a natureza dos buracos negros são: geometria diferencial, equações de Einstein e poderosos métodos analíticos e numéricos usados ​​para resolver as equações de Einstein e descrever a geometria espaço-temporal que os buracos negros geram. E assim que pudermos dar uma descrição quantitativa completa do espaço-tempo gerado pelo buraco negro, do ponto de vista astrofísico, o tópico dos buracos negros poderá ser considerado fechado. Numa perspectiva teórica mais ampla, ainda existem muitas oportunidades de pesquisa. O objetivo deste capítulo é falar sobre algumas realizações teóricas da física moderna dos buracos negros, nas quais as idéias da termodinâmica e da teoria quântica são combinadas com a teoria geral da relatividade, dando origem a novos conceitos inesperados. A idéia básica é que os buracos negros não são apenas objetos geométricos. Eles têm uma temperatura, uma enorme entropia e podem exibir manifestações de entrelaçamento quântico. Nossa discussão sobre os aspectos termodinâmicos e quânticos da física dos buracos negros será mais superficial e superficial do que a análise de características do espaço-tempo puramente geométricas nos buracos negros apresentados nos capítulos anteriores. Mas esses aspectos, e principalmente o quantum, são uma parte essencial e vital dos estudos teóricos em andamento dos buracos negros, e nos esforçaremos muito para transmitir, se não detalhes complicados, pelo menos o espírito desses trabalhos.

Na teoria geral clássica da relatividade - se falarmos da geometria diferencial das soluções das equações de Einstein - os buracos negros são verdadeiramente negros no sentido de que nada pode sair deles. Stephen Hawking mostrou que essa situação muda completamente quando levamos em conta os efeitos quânticos: os buracos negros emitem radiação de uma certa temperatura, conhecida como temperatura de Hawking. Para buracos negros de tamanho astrofísico (ou seja, de buracos negros de massas estelares a supermassivos), a temperatura de Hawking é insignificante em comparação com a temperatura do fundo cósmico de microondas - radiação preenchendo todo o Universo, que, por sinal, pode ser considerada uma variante da radiação de Hawking. Os cálculos realizados por Hawking para determinar a temperatura dos buracos negros fazem parte de um programa de pesquisa mais amplo no campo chamado termodinâmica dos buracos negros. Outra parte importante deste programa é o estudo da entropia de buracos negros, que caracteriza a quantidade de informação perdida dentro de um buraco negro. Objetos comuns (como uma caneca de água, uma barra de magnésio puro ou uma estrela) também têm entropia, e uma das afirmações centrais da termodinâmica dos buracos negros é que um buraco negro desse tamanho tem mais entropia do que qualquer outra forma de matéria que possa ser acomodada. uma área do mesmo tamanho, mas sem a formação de um buraco negro.

Mas antes de nos aprofundarmos na discussão dos problemas associados à radiação Hawking e à entropia dos buracos negros, vamos fazer uma rápida excursão aos campos da mecânica quântica, termodinâmica e emaranhamento. A mecânica quântica foi desenvolvida principalmente na década de 1920, e seu principal objetivo era descrever partículas muito pequenas de matéria, como átomos. O desenvolvimento da mecânica quântica levou à erosão de conceitos básicos da física como a posição exata de uma partícula individual: verificou-se, por exemplo, que a posição de um elétron quando se move ao redor de um núcleo atômico não pode ser determinada com precisão. Em vez disso, as chamadas órbitas foram atribuídas aos elétrons, nos quais suas posições reais só podem ser determinadas em um sentido probabilístico. Para nossos propósitos, no entanto, é importante não avançarmos rapidamente para esse lado probabilístico. Veja o exemplo mais simples: um átomo de hidrogênio. Pode estar em um certo estado quântico. O estado mais simples de um átomo de hidrogênio, chamado estado fundamental, é o estado com a menor energia e essa energia é precisamente conhecida. Em um sentido mais geral, a mecânica quântica nos permite (em princípio) conhecer o estado de qualquer sistema quântico com absoluta precisão.

As probabilidades surgem quando fazemos um certo tipo de pergunta sobre um sistema mecânico quântico. Por exemplo, se é definitivamente sabido que o átomo de hidrogênio está no estado fundamental, podemos perguntar: "Onde está o elétron?" e de acordo com as leis da quantum
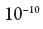
mecânica chegamos a essa pergunta apenas uma certa estimativa de probabilidade, aproximadamente algo como: "o elétron provavelmente está localizado a uma distância de até meio angstrom do núcleo de um átomo de hidrogênio" (um angstrom é igual a metros). Mas temos a oportunidade, através de um certo processo físico, de encontrar a posição do elétron com muito mais precisão do que um angstrom. Esse processo, que é bastante comum na física, consiste em lançar um fóton com comprimento de onda muito curto em um elétron (ou, como dizem os físicos, espalhar um fóton em um elétron) - depois disso, podemos reconstruir a localização do elétron no momento da dispersão com uma precisão aproximadamente igual ao comprimento de onda fóton. Mas esse processo mudará o estado do elétron, de modo que depois disso não estará mais no estado fundamental do átomo de hidrogênio e não terá uma energia definida com precisão. Mas, por algum tempo, sua posição será quase exatamente determinada (precisa do comprimento de onda do fóton usado para isso). Uma avaliação preliminar da posição do elétron pode ser realizada apenas no sentido probabilístico, com uma precisão de cerca de um angstrom, mas, assim que o medimos, sabemos exatamente o que era igual. Em resumo, se medirmos um sistema mecânico quântico de alguma maneira, então, pelo menos no sentido geralmente aceito, "forçadamente" damos a ele um estado com um certo valor da quantidade que estamos medindo.

A mecânica quântica é aplicável não apenas aos pequenos, mas (como acreditamos) a todos os sistemas, mas para sistemas grandes, as regras da mecânica quântica rapidamente se tornam muito complexas. O conceito principal é o entrelaçamento quântico, um exemplo simples do qual é o conceito de rotação (rotação). Os elétrons individuais têm um giro, portanto, na prática, um único elétron pode ter um giro direcionado para cima ou para baixo em relação ao eixo espacial selecionado. O spin do elétron é uma quantidade observada, porque o elétron gera um campo magnético fraco, semelhante ao campo de uma barra magnética. Então, um giro apontando para cima significa que o pólo norte do elétron está apontando para baixo, e um giro apontando para baixo significa que o pólo norte está "olhando para cima". Dois elétrons podem ser colocados em um estado quântico conjugado, no qual um deles tem um spin direcionado para cima e outro para baixo, mas é impossível dizer qual dos elétrons tem qual spin. De fato, no estado fundamental de um átomo de hélio, dois elétrons estão exatamente nesse estado, chamado spin-singuleto, uma vez que o spin total de ambos os elétrons é igual a zero. Se separarmos esses dois elétrons sem alterar seus spins, poderemos continuar afirmando que eles são spin-singletos juntos, mas ainda não podemos dizer qual será o spin de cada um deles individualmente. Agora, se medirmos um de seus giros e estabelecermos que ele está direcionado para cima, teremos certeza absoluta de que o segundo está direcionado para baixo. Nesta situação, dizemos que as costas estão enredadas - nenhuma em si tem um significado definido, enquanto juntas elas estão em um estado quântico definido.

Einstein estava muito preocupado com o fenômeno do emaranhado: parecia ameaçar os princípios básicos da teoria da relatividade. Vamos considerar o caso de dois elétrons em um estado spin-singuleto, quando estão distantes um do outro no espaço. Por definição, deixe um deles levar Alice e o outro Bob. Suponha que Alice medisse a rotação do elétron e descobrisse que era para cima, e Bob não medisse nada. Até Alice concluir sua medição, era impossível dizer qual era a rotação do elétron dele. Mas assim que ela completou sua medição, ela sabia que o spin do elétron de Bob é direcionado para baixo (na direção oposta ao spin de seu próprio elétron). Isso significa que sua medição transferiu instantaneamente o elétron de Bob para o estado em que seu spin é direcionado para baixo? Como isso poderia acontecer se os elétrons são separados espacialmente? Einstein e seus colegas de trabalho Nathan Rosen e Boris Podolsky acharam que a história de medir sistemas emaranhados era tão séria que ameaçava a própria existência da mecânica quântica. O paradoxo de Einstein - Podolsky - Rosen (EPR) formulado por eles usa um experimento mental semelhante ao que acabamos de descrever para concluir: a mecânica quântica não pode ser uma descrição completa da realidade. Agora, com base na pesquisa teórica que se seguiu e em muitas medidas, uma opinião comum foi estabelecida de que o paradoxo da EPR contém um erro e que a teoria quântica está correta. O emaranhamento mecânico-quântico é real: as medidas dos sistemas emaranhados se correlacionam, mesmo que esses sistemas estejam distantes no espaço-tempo.

Voltemos à situação em que colocamos dois elétrons em um estado de spin-singlete e os distribuímos para Alice e Bob. O que podemos dizer sobre elétrons antes de serem realizadas as medições? Que ambos juntos estão em um certo estado quântico (spin-singuleto). É provável que o giro do elétron Alicin seja direcionado para cima ou para baixo. Mais precisamente, o estado quântico de seu elétron com a mesma probabilidade pode ser um (girar para cima) ou outro (girar para baixo). Agora, para nós, o conceito de probabilidade assume um significado mais profundo do que antes. Antes, consideramos um determinado estado quântico (o estado fundamental de um átomo de hidrogênio) e vimos que existem algumas perguntas "desconfortáveis", como "Onde está localizado o elétron?", Perguntas cujas respostas existem apenas no sentido probabilístico. Se fizéssemos perguntas “boas”, por exemplo: “Qual é a energia desse elétron?”, Obteríamos certas respostas para elas. Agora, não há perguntas "boas" que possamos fazer sobre o elétron de Alice, cujas respostas não dependeriam do elétron de Bob. (Não estamos falando de perguntas estúpidas como "O elétron de Alice gira?" - perguntas para as quais há apenas uma resposta.) Portanto, teremos que usar uma linguagem probabilística para determinar os parâmetros de um dos sistemas semi-confusos. A certeza surge apenas quando consideramos a conexão entre perguntas que Alice e Bob podem fazer sobre seus elétrons.

Começamos propositadamente com um dos sistemas mais simples de mecânica quântica que conhecemos: os sistemas de rotação de elétrons individuais. Espera-se que os computadores quânticos sejam construídos com base em sistemas tão simples. O sistema de spin de elétrons individuais ou outros sistemas quânticos equivalentes agora é chamado de qubits (abreviação de "bits quânticos"), que enfatiza seu papel em computadores quânticos, semelhante ao papel desempenhado por bits comuns em computadores digitais.

Imagine agora que substituímos cada elétron por um sistema quântico muito mais complexo por muitos, e não apenas dois estados quânticos. Por exemplo, eles deram a Alice e Bob barras de puro magnésio. Antes de Alice e Bob seguirem caminhos separados em diferentes direções, suas barras podem interagir, e concordaremos que, ao fazê-lo, eles adquirem um certo estado quântico geral. Assim que Alice e Bob divergem, suas barras de magnésio param de interagir. Como no caso dos elétrons, cada barra está em um estado quântico indefinido, embora juntas, como acreditamos, elas formem um estado completamente definido. (Nesta discussão, assumimos que Alice e Bob são capazes de mover suas barras de magnésio sem perturbar seu estado interno, da mesma forma que anteriormente pensávamos que Alice e Bob poderiam separar seus elétrons emaranhados sem alterar suas rotações.) Mas a diferença entre esse experimento mental e o experimento com elétrons é que a incerteza no estado quântico de cada barra é enorme. Uma barra pode muito bem adquirir mais estados quânticos que o número de átomos no universo. É aqui que a termodinâmica entra em cena. Sistemas definidos de maneira muito imprecisa podem, no entanto, ter algumas características macroscópicas bem definidas. Essa característica é, por exemplo, temperatura. Temperatura é uma medida da probabilidade com que qualquer parte de um sistema possui uma certa energia média, com uma temperatura mais alta correspondente a uma maior probabilidade de ter mais energia. Outro parâmetro termodinâmico é a entropia, que é essencialmente igual ao logaritmo do número de estados que o sistema pode receber. Outra característica termodinâmica que seria significativa para uma barra de magnésio é a sua magnetização total, ou seja, em essência, um parâmetro que mostra quanto mais elétrons podem estar na barra com a rotação apontando para cima do que com a rotação apontando para baixo.

Envolvemos a termodinâmica em nossa história como uma maneira de descrever sistemas cujos estados quânticos não são exatamente conhecidos devido ao seu envolvimento com outros sistemas. A termodinâmica é uma ferramenta poderosa para analisar esses sistemas, mas seus criadores não esperavam tal aplicação. Sadi Carnot, James Joule, Rudolph Clausius eram os líderes da revolução industrial do século XIX e estavam interessados ​​na sua mais prática de todas as questões: como funcionam os motores? Pressão, volume, temperatura e calor são a carne e o sangue dos motores. Carnot descobriu que a energia na forma de calor nunca pode ser completamente transformada em trabalho útil, como levantar mercadorias. Parte da energia será sempre desperdiçada. Clausius deu a principal contribuição para a criação da idéia de entropia como uma ferramenta universal para determinar as perdas de energia durante qualquer processo associado ao calor. Sua principal conquista foi a constatação de que a entropia nunca diminui - em quase todos os processos que ela cresce. Processos nos quais os aumentos de entropia são chamados irreversíveis - precisamente porque eles não podem reverter sem diminuir a entropia. O próximo passo no desenvolvimento da mecânica estatística foi realizado por Clausius, Maxwell e Ludwig Boltzmann (entre muitos outros) - eles mostraram que a entropia é uma medida de desordem. Normalmente, quanto mais você age sobre algo, mais você mexe lá em cima. E mesmo que você tenha desenvolvido um processo cujo objetivo é restaurar a ordem, no decorrer dela, mais entropia se formará inevitavelmente do que será destruída, por exemplo, quando o calor é liberado. O guindaste, que empilha as vigas de aço em perfeita ordem, cria ordem em termos de localização das vigas, mas tanto calor será liberado durante sua operação que a entropia total ainda aumenta.

Mas ainda assim, a diferença entre a visão sobre a termodinâmica dos físicos do século XIX e a visão associada ao entrelaçamento quântico não é tão grande quanto parece. Cada vez que um sistema interage com um agente externo, seu estado quântico é confundido com o estado quântico do agente. Geralmente esse emaranhamento leva a um aumento na incerteza do estado quântico do sistema, em outras palavras, a um aumento no número de estados quânticos nos quais o sistema pode estar. Como resultado da interação com outros sistemas, a entropia, definida em termos da quantidade de estados quânticos disponíveis para o sistema, geralmente cresce.

Em geral, a mecânica quântica fornece uma nova maneira de caracterizar sistemas físicos nos quais alguns parâmetros (por exemplo, posição no espaço) se tornam incertos, enquanto outros (por exemplo, energia) são frequentemente conhecidos exatamente. No caso do emaranhamento quântico, duas partes fundamentalmente separadas do sistema têm um estado quântico comum conhecido e cada parte separadamente é um estado indefinido. Um exemplo padrão de emaranhamento é um par de giros em um estado singleto no qual é impossível dizer qual rotação é direcionada para cima e qual é para baixo. , , , , .

, , , , . — , , , 2π. , , , ‑. , , , . : - ? , , , . , , 6 . , ( , ) . , 1,5 , . , , , , ; , , . , , . ( « , …», , , , .) , , : , , , , , , . , , , , , , , , . : ! , , , , , . , , , , , , . , -. , , - , .

, - , - . , , - : , . , , , , -, . , - , (, , , ). -, , , , , . - , . , 60 . , , ( ) ,



. 7.1 , a . , , t = 0. , t = 0 . , ‑.

, , « ». ? ? , . , , , . — , — , , . -, , ‑. - , , . , !

, , , — , , . «» , «», , , . 2, , , , . , , . , , ? , . , ? , , , . , , .