Entropia de informações do caos

1. Introdução

Existem muitas publicações sobre Habr nas quais o conceito de entropia é considerado, aqui estão apenas algumas delas [1]. As publicações foram recebidas positivamente pelos leitores e despertaram grande interesse. É suficiente dar a definição de entropia dada pelo autor da publicação [1]: “entropia é quanta informação você não conhece sobre o sistema”. Publicações sobre o fenômeno do caos em Habr também são suficientes [6–9]. No entanto, a relação de entropia e caos em ambos os grupos de publicações não foi considerada.

Isso se deve ao fato de que diferentes áreas do conhecimento distinguem diferentes tipos de medidas de caos:

• informativo;
• termodinâmico;
• diferencial;
• cultural.

As medidas de caos também são descritas levando em consideração sua especificidade, mesmo em uma dessas áreas é bastante difícil.

Tentando simplificar ao máximo a tarefa, decidi considerar a relação entre entropia informacional e caos usando o exemplo da semelhança das regiões de passagem da ordem ao caos nos diagramas na forma de mapeamentos de pontos e nos gráficos do coeficiente de entropia para essas regiões.

O que veio disso você aprenderá olhando sob o gato.

Os mecanismos de transição da ordem para o caos

Uma análise dos mecanismos de transição da ordem para o caos em sistemas reais e vários modelos revelou a universalidade de relativamente poucos cenários de transição para o caos. A transição para o caos pode ser representada na forma de um diagrama de bifurcação (o termo “bifurcação” é usado para denotar rearranjos qualitativos do sistema com o surgimento de um novo modo de comportamento).

A entrada do sistema no modo imprevisível é descrita por uma cascata de bifurcações após uma após a outra. A cascata de bifurcações leva sequencialmente a uma escolha entre duas soluções, depois quatro e assim por diante, o sistema começa a oscilar em um modo caótico e turbulento de duplicar sequencialmente o número de valores possíveis.

Consideramos as bifurcações da duplicação de períodos e o aparecimento do caos nos mapeamentos de pontos. Display é uma função que mostra a dependência dos seguintes valores dos parâmetros do sistema em relação aos valores anteriores:

$$$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$

Considere também a segunda função comumente usada:

$$$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

Usando mapeamentos de pontos, os objetos são estudados não com contínuo, mas com tempo discreto . Após a transição para a tela, a dimensão do sistema em estudo pode diminuir.

Ao alterar o parâmetro externo \ lambda, os mapeamentos de pontos exibem um comportamento bastante complicado, que se torna caótico com \ lambda suficientemente grande. O caos é uma recessão muito rápida de trajetórias no espaço de fase.

A bifurcação é uma reestruturação qualitativa do filme. Os valores do parâmetro de controle no qual ocorrem as bifurcações são chamados de valores críticos ou de bifurcação.

Para criar os diagramas, usaremos as duas listagens a seguir:

No. 1. Para função: $$$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$


No. 2. Para função $$$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$


Avaliar o impacto da natureza da função logística em valores críticos $$$\ lambda$ considere diagramas com uma função $$$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ Para fazer isso, usaremos a listagem nº 1:

Para 0 <\ lambda <1 para $$$\ lambda = $ 0,9$ e x0 = 0,47, obtemos o diagrama:



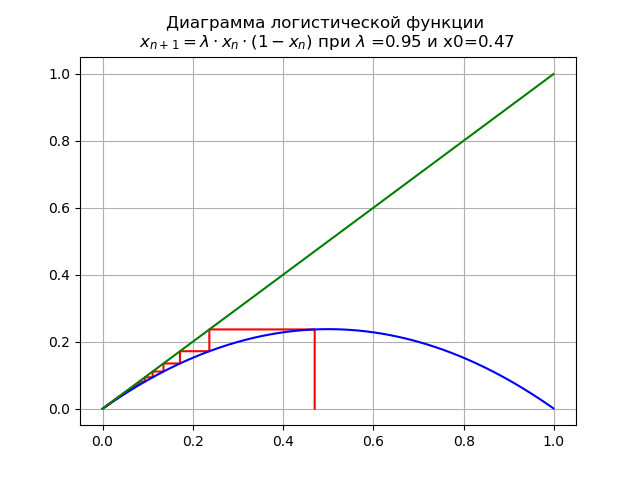
Nesse caso, o mapa possui um único ponto fixo $$$x ^ {*} = 0$
que é sustentável.

At $$$1 <\ lambda <3$ para $$$\ lambda = $ 2,$ x0 = 0,7, obtemos o diagrama:



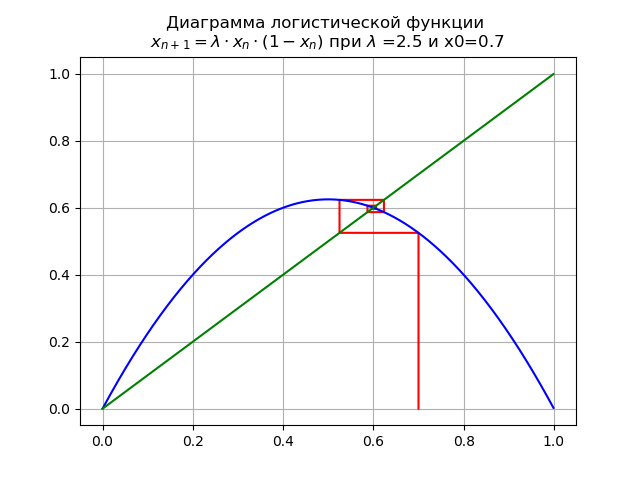
No segmento [0, 1], outro ponto fixo fixo aparece $$$x_ {1} ^ {*} = 1-1 / \ lambda$

At $$$1 <\ lambda <3$ para $$$\ lambda = $ 2,$ e x0 = 0,01, obtemos o diagrama:



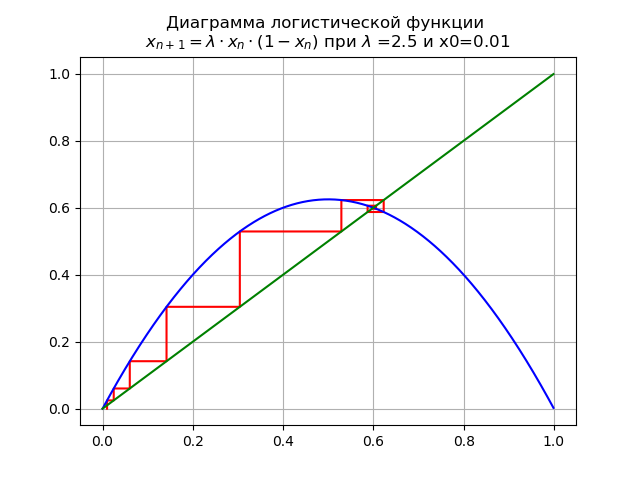
Ponto fixo $$$x ^ {*} = 0$ perde estabilidade.

At $$$3 <\ lambda <3,45$ para $$$\ lambda = $ 3,4$ e x0 = 0,7, obtemos o diagrama:



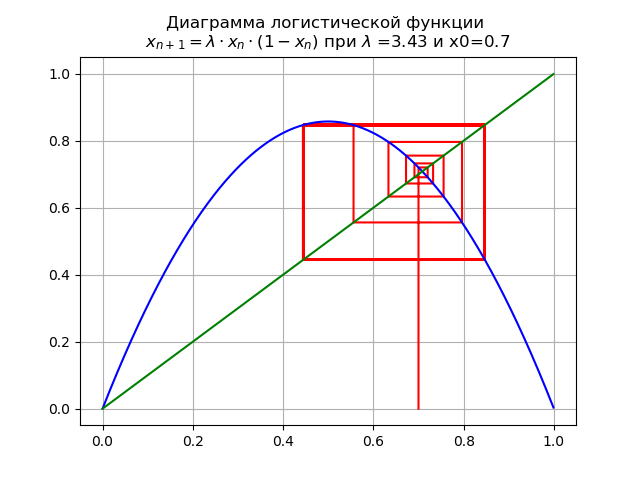
O mapeamento sofre uma bifurcação: ponto fixo $$$x_ {1} ^ {*}$ torna-se instável e um ciclo duplo é exibido.

At $$$3,45 <\ lambda <4,0$ para $$$\ lambda = $ 3,5$
e x0 = 0,2, obtemos o diagrama:



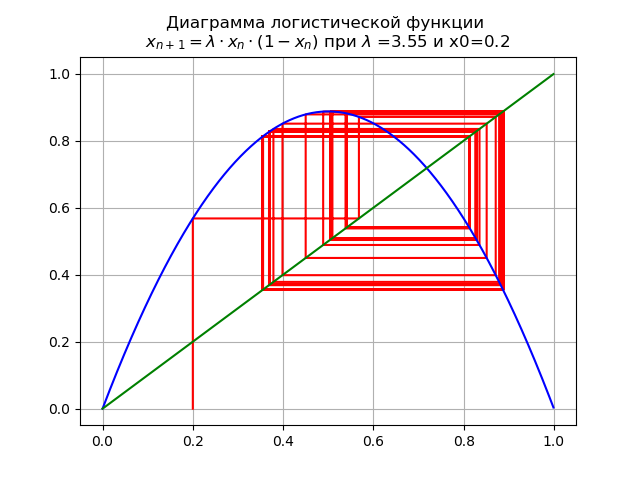
Ao passar um parâmetro $$$\ lambda$ através do valor $$$\ lambda = 3,45$ , Um ciclo de duas vezes se torna quatro vezes e além.

No valor final $$$\ lambda = 4$ o sistema possui ciclos instáveis ​​de todos os pedidos possíveis:



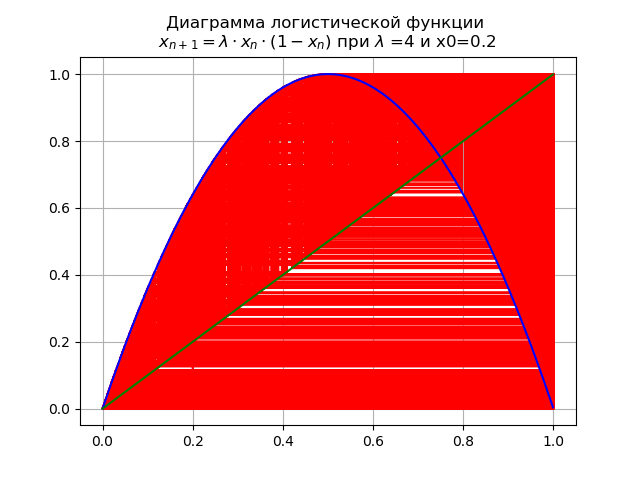
Avaliar o impacto da natureza da função logística em valores críticos $$$\ lambda$ considere diagramas com uma função $$$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$ , para isso, usaremos a listagem nº 2.

At $$$0 <\ lambda <= 1,0$ para $$$\ lambda = 0,5$ e x0 = 0,2:



O mapeamento possui um único ponto fixo $$$x ^ {*} = 0$ que é sustentável.

At $$$1 <\ lambda <= 1.998 ...$ para $$$\ lambda = $ 1,$ e x0 = 0,55:



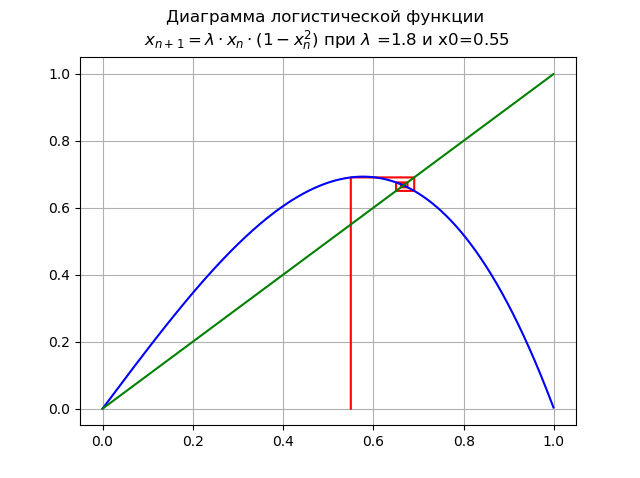
Ponto $$$x ^ {*} = 0$ perde a estabilidade, um novo ponto estável aparece $$$x_ {1} ^ {*}$

At $$$1,99 <\ lambda <= 2,235 ...$ para $$$\ lambda = US $ 2,$ e x0 = 0,2:



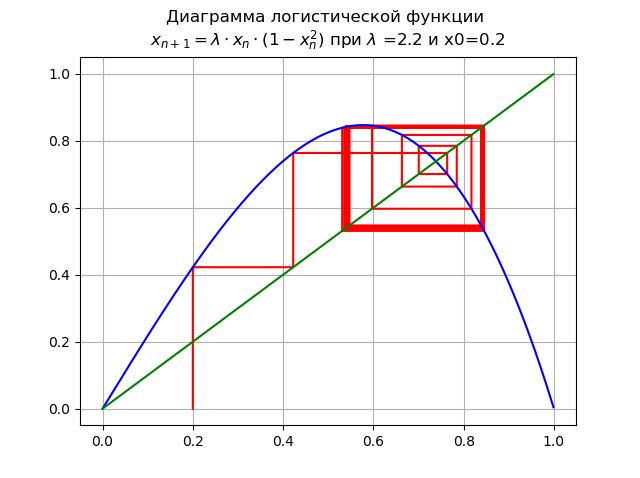
Bifurcação da duplicação do período ocorre, um ciclo de 2 vezes aparece. Aumento adicional $$$\ lambda$ leva a uma cascata de períodos de duplicação de bifurcações.

At $$$2,235 <\ lambda 2.5980 ...$ para $$$\ lambda = 2,287$ e x0 = 0,2:



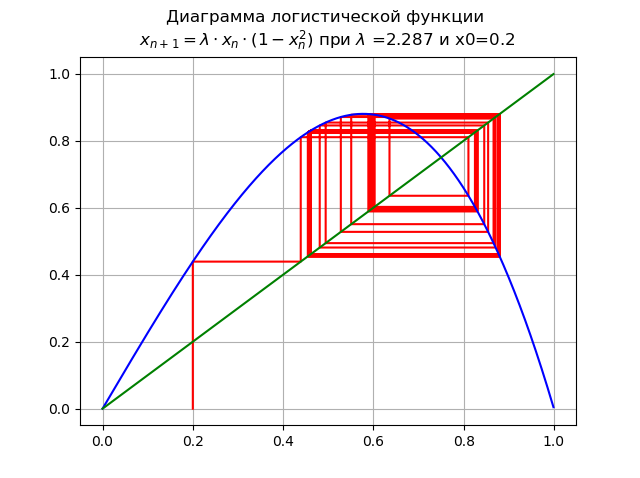
Aumentar $$$\ lambda$ levou a uma cascata de período dobrando bifurcações.

At $$$\ lambda = 2,59$ o sistema possui ciclos instáveis ​​de todos os períodos possíveis:



Como foi mostrado nos diagramas, com um aumento na ordem da função logística, o intervalo de mudanças $$$\ lambda$ diminui.

Usando diagramas, traçamos o caminho do pedido ao caos, enquanto definimos os valores $$$\ lambda$ para diferentes funções logísticas. Resta responder à pergunta: como medir o caos? A resposta para alguns dos tipos de caos listados no início do artigo é conhecida
- entropia é uma medida do caos. Esta resposta pode ser totalmente atribuída ao caos da informação, no entanto, que entropia é aplicada aqui e como comparar com o valor numérico já considerado $$$\ lambda$ - Tentarei responder a essa pergunta na próxima parte do artigo.

Entropia de informação e coeficiente de entropia

Consideraremos a entropia binária de informações para eventos aleatórios independentes. $$$x$ c $$$n$ possíveis estados distribuídos com probabilidades $$$p_ {i} (i = 1, .., n)$ . A entropia binária de informações é calculada pela fórmula:

$$$H (x) = - \ sum_ {i = 1} ^ {n} p_ {i} \ cdot log_ {2} (p_ {i})$

Esse valor também é chamado de entropia média da mensagem. Valor $$$H_ {i} = - log_ {2} (p_ {i})$ chamada entropia privada, caracterizando apenas o i- ésimo estado. No caso geral, a base do logaritmo na definição de entropia pode ser maior que 1; sua escolha determina a unidade de medida da entropia.

Usaremos logaritmos decimais nos quais a entropia e as informações são medidas em bits. A quantidade de informações em bits será calculada corretamente quando, por exemplo, variáveis $$$X$ e $$$\ Delta$ será substituído nas expressões correspondentes por entropia, não importa em qual, mas sempre nas mesmas unidades. De fato:

$$$q = H (x) -H (\ Delta) = log_ {10} \ left (X_ {2} -X_ {1} \ right) -log_ {10} (2 \ Delta) = log_ {10} (\ frac {X_ {2} -X_ {1}} {2 \ Delta})$

onde X e $$$\ Delta$ deve estar nas mesmas unidades.

Uma estimativa do valor da entropia de uma variável aleatória a partir de dados experimentais é encontrada em um histograma da seguinte relação:

$$$\ Delta_ {e} = \ frac {1} {2} e ^ {H (x)} = \ frac {d} {2} \ prod_ {i = 1} ^ {m} (\ frac {n} { n_ {i}}) ^ {\ frac {n_ {i}} {n}} = \ frac {dn} {2} 10 ^ {- \ frac {1} {n}} \ sum_ {i = 1} ^ {m} n_ {i} log_ {10} (n_ {i})$

onde: $$$d$ –Largura de cada coluna do histograma; $$$m$ - número de colunas; $$$n$ quantidade total de dados; $$$n_ {i}$ - quantidade de dados em $$$i$ essa coluna.

O coeficiente de entropia é determinado a partir da razão:

$$$k_ {e} = \ frac {\ Delta_ {e}} {\ sigma}$

onde: $$$\ sigma$ desvio padrão.

Entropia da informação como uma medida do caos

Para analisar os fenômenos do caos da informação usando o coeficiente de entropia, primeiro criamos um diagrama de ramificações para a função $$$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ com a aplicação de áreas de transição obtidas durante a construção de histogramas:


Temos:



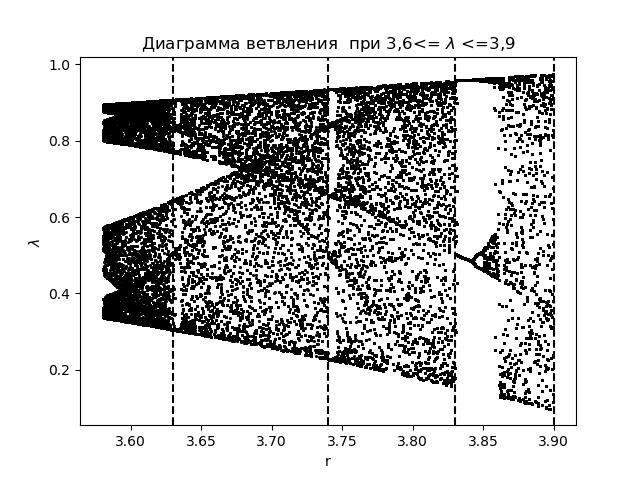
Traçamos o coeficiente de entropia para as mesmas áreas $$$\ lambda$ :


Temos:



Comparando o diagrama e o gráfico, vemos uma exibição idêntica das regiões no diagrama e no gráfico para o coeficiente de entropia para a função $$$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ .

Para uma análise mais aprofundada dos fenômenos do caos da informação usando o coeficiente de entropia, criamos um diagrama de ramificações para a função logística: $$$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$ com a aplicação de áreas de transição:


Temos:



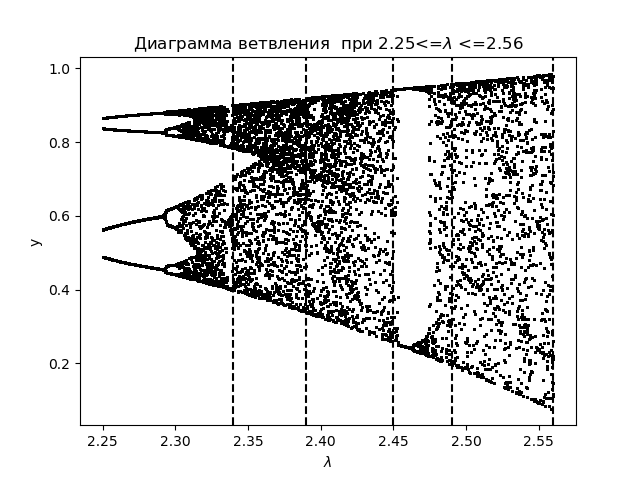
Traçamos o coeficiente de entropia para as mesmas áreas $$$\ lambda$ :


Temos:



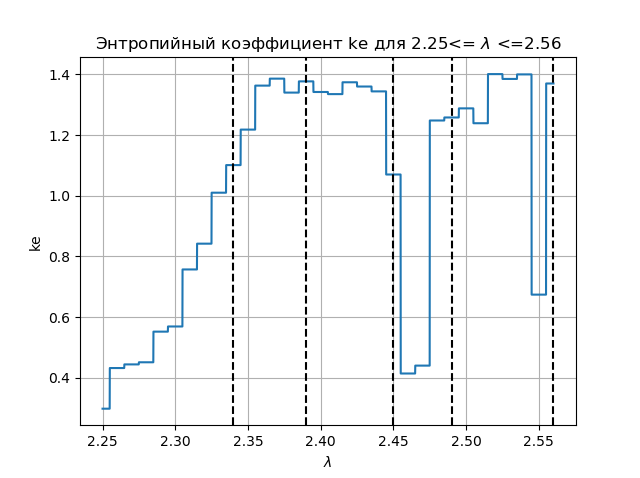
Comparando o diagrama e o gráfico, vemos uma exibição idêntica das regiões no diagrama e no gráfico para o coeficiente de entropia para a função $$$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

Conclusões:

O problema educacional é resolvido no artigo: a entropia informacional é uma medida do caos, e a resposta dessa pergunta é afirmativamente dada por Python.

Referências

1. Entropia? É fácil!
2. Introdução ao conceito de entropia e suas múltiplas faces.
3. Árvores de entropia e decisão.
4. Um tratado sobre entropia.
5. Entropia e WinRAR.
6. Modelos matemáticos do caos.
7. Um pouco sobre o caos e como criá-lo.
8. Um olhar crítico sobre o atrator Lorenz.
   
9. Geradores de caos em FPGA.