Na estimativa autoregressiva da densidade espectral de um sinal estacionário

Métodos de estimação espectral de processos aleatórios estacionários baseados na transformada rápida de Fourier (FFT) são bem conhecidos e amplamente utilizados na prática de engenharia. Suas desvantagens incluem, em particular, uma alta dispersão (baixa precisão) da estimativa com um intervalo de observação insuficientemente longo para o processo, que geralmente se manifesta visualmente em um forte gráfico "recuado" da densidade espectral de potência (PSD). Um dos métodos alternativos de estimativa espectral é o método auto-regressivo, considerado no exemplo abaixo, que é muito menos conhecido na prática de engenharia. Em muitos casos, o método torna relativamente fácil obter uma estimativa muito melhor do PSD (Fig. 1) e, às vezes, informações ainda mais profundas sobre o processo aleatório em estudo.


Fig. 1 Avaliação clássica e autorregressiva do processo “curto” PSD

Para fins de demonstração, um sinal de tempo discreto (sequência) x [i] foi sintetizado. O sinal é modelado usando um modelo ARMA (filtro digital) simulando as propriedades de um sistema mecânico (1) - movendo o ponto de material x (t) em um oscilador de "massa única" com parâmetros m = 1 kg, c = 100 N / m, k = 2, 5 kg / s, e por uma perturbação da força - ruído gaussiano “branco” (levando em consideração a discretização) f (t) com uma dispersão de 1 N ² , intervalo de amostragem no tempo Δt = 0,12 s.



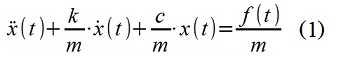
Modelo construído (2). O método de construção do modelo já foi considerado anteriormente aqui .

x [i] - 0,6388 · x [i-1] + 0,7408 · x [i-2] = 0,009667 · f [i-1] (2)

Usando (2), uma sequência de 50 mil amostras foi sintetizada, para a qual foi usado um gerador de uma variável aleatória aleatória distribuída normalmente () de um ambiente de software conhecido.

Após a simulação do processo x [i], os parâmetros quantitativos do modelo (2) são assumidos como desconhecidos - apenas o processo em si e, em certa medida, informações sobre as propriedades do modelo em termos gerais estão disponíveis para pesquisa.

Uma estimativa espectral da seqüência de 50.000 pontos foi realizada usando o método Welch, o tamanho do segmento foi igual a 256 amostras, a janela de Hamming e a sobreposição de 60% dos segmentos foi aplicada. O desvio padrão de tal estimativa, com base no fato de que a sequência tem um comprimento de cerca de 200 segmentos não sobrepostos, pode ser estimado aproximadamente como ~ 7%.

Além disso, supondo que, em condições reais do experimento, uma sequência muito mais curta esteja disponível para pesquisa, os estudos foram realizados apenas nas primeiras 500 amostras desse sinal.

Uma estimativa é obtida pelo método Welch com os mesmos parâmetros. O desvio padrão de tal estimativa é de ~ 70%; uma “rugosidade” muito forte do gráfico é perceptível (Fig. 2).


Fig. 2. Avaliação do PSD dos processos “longo” e “curto” pelo método clássico

Com base no fato de sabermos a forma aproximada da função (gráfico) do processo SPM (por exemplo, com base na natureza física conhecida do processo - um oscilador de massa única sob ruído branco ou na avaliação de processos semelhantes para os quais há implementações mais longas disponíveis), decidimos usando o modelo autoregressivo de segunda ordem (AR (2) ou = ARMA (2.0)).

Determinar a ordem do modelo é um ponto muito importante; um erro na ordem pode levar a erros muito grosseiros nos resultados da estimativa. Existem métodos que ainda não são considerados aqui, ajudando a determinar a ordem do modelo com base apenas no processo que está sendo analisado.

A estimativa dos parâmetros do modelo foi realizada usando as conhecidas equações de Yule-Walker para o processo autoregressivo (ligeiramente modificado para simplificar ligeiramente a estrutura do script):



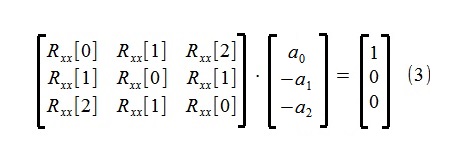
Como pode ser visto nas equações, para determinar os parâmetros, apenas os três primeiros membros da sequência autoregressiva Rxx [0], Rxx [1], Rxx [2], que foram estimados a partir da sequência inicial de 500 pontos x [i] pelo método do correlograma, são utilizados ~ 4,5%.

(A propósito, é claro que os "contras" antes de ₁ , a2 ₂ etc. são extremamente inconvenientes. Apareceram devido ao uso predominantemente "preditivo" dos modelos ARMA na economia, em suas fontes anteriores de "engenharia". Não. Eu já duvido que fosse necessário usar essa compreensão dos coeficientes de RA aqui.)

A matriz de correlação em (3) na prática sempre tem uma prevalência diagonal estrita | Rxx [0] > Rxx [i] |, inclusive devido à presença de ruídos de observação, em resultado dos quais não há dificuldades com seu manuseio (encontrar uma solução (3)).

(Para esclarecer a questão da magnitude do erro de modelagem estatística, é interessante mencionar, por exemplo, a estimativa Rxx [0] = 2.2606e-04 m ² obtida de 500 amostras, em comparação com a estimativa de dispersão do correlograma obtida de 50.000 amostras, = 2,4238e-04 m ² e a estimativa pelo integrando da área de PSD obtida pelo método de Welch para 50.000 amostras (Fig. 2) = 2,4232e-04 m ² )

Após substituir as estimativas encontradas Rxx [i], temos:



Os seguintes parâmetros do modelo são determinados como ₀ = 11325.9; a ₁ = 7090,1; a ₂ = -8411,5; Como pode ser visto em (3), a dispersão do ruído branco de entrada hipotético foi ajustada = 1 aqui, determinando em vez dele o ganho a ₀ . Uma estimativa autoregressiva do PSD é construída pela transformada de Fourier sobre uma sequência de coeficientes a ₀ , a ₁ , a ₂ :




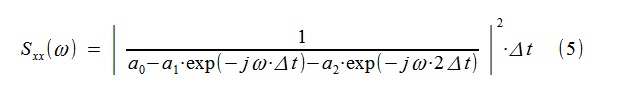
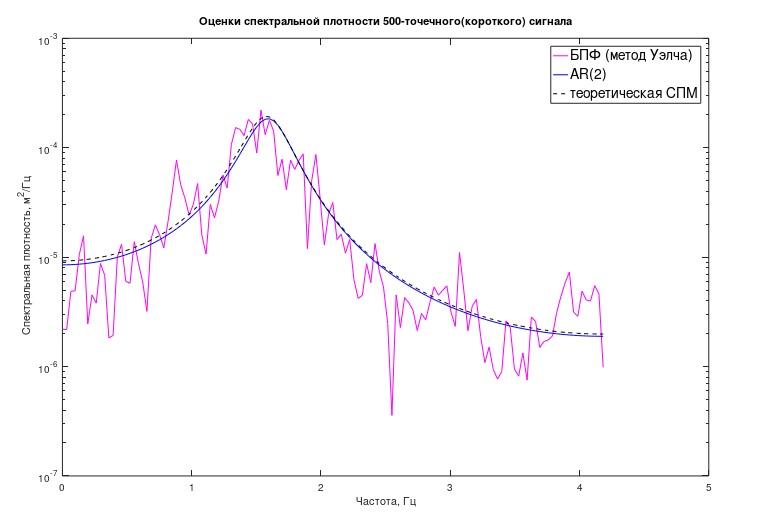Fig. 3 Avaliação clássica e autorregressiva do processo "curto" PSD

Da mesma forma, de acordo com uma expressão semelhante a (5), o cronograma "teórico" do PSD foi construído anteriormente, apenas os coeficientes do modelo ali, é claro, foram tomados diferentes (de (2)).
Pode-se ver no gráfico que a estimativa de RA do PSD estava muito próxima da estimada teoricamente. Além do gráfico, é possível tentar avaliar algumas características analíticas do processo e do sistema mecânico associado. Nesse caso, esses são os "polos" do modelo, caracterizando numericamente as frequências dos picos "ressonantes" do modelo e os "fatores de qualidade" associados.

Em (5), encontramos a relação para pesquisar as descontinuidades da função de transferência do nosso modelo usando a transformada de Laplace (substituindo jω por λ = -ε + jω):



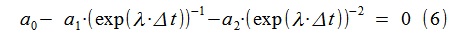
Para o modelo de RA obtido, foi calculado λ _1,2 = -1,5427 ± j · 10,1514, o que é muito próximo ao modelo original usado para gerar o processo
λ _1.2theor = -1.2500 ± j.9.9216 (isto é, as posições do pico de ressonância, respectivamente, 1.615 Hz (em teoria) e 1.579 Hz (determinado)).


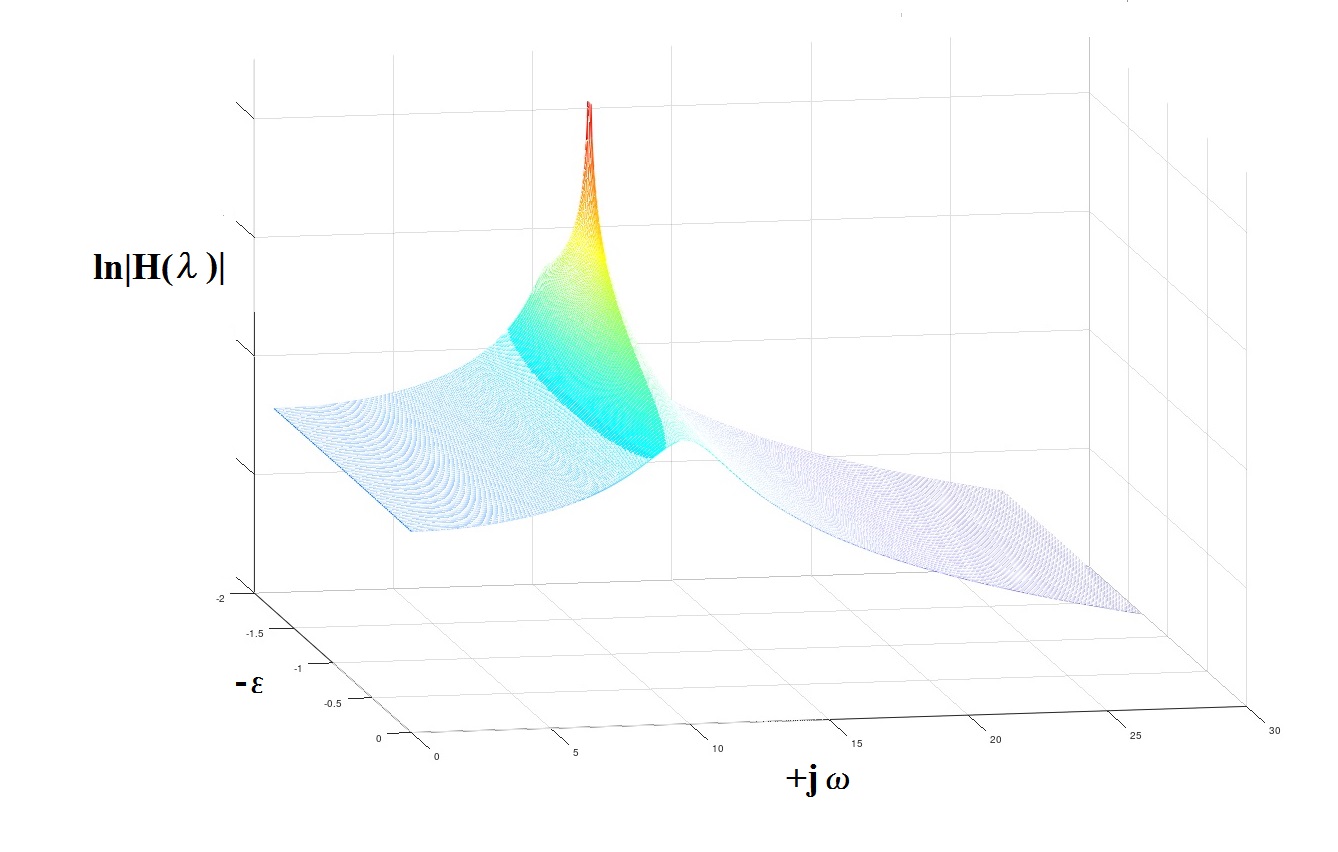Fig. 4 Sobre o conceito de "postes"

Alguns comentários e recomendações em conclusão.

1. A ordem “excessiva” (muito grande) do modelo de RA é geralmente muito menos perigosa do que insuficiente, do ponto de vista do risco de obter uma estimativa de PSD com erros grosseiros.
2. Como regra, a modelagem de AR torna possível determinar com bastante precisão as frequências ressonantes jω _k e determinar com muito menos precisão as larguras dos "picos" correspondentes- _k
3. ARMA - o modelo pode ter uma ordem (tamanho) muito menor do que o modelo AR, que parece ter como objetivo melhorar a precisão do modelo, de acordo com muitas fontes. No entanto, avaliar a parte MA do modelo é muito mais difícil e geralmente pode incluir o primeiro passo na obtenção de um modelo AR de ordem grande, a fim de transformá-lo ainda mais na parte MA. Em conexão com essas fontes, também se expressa uma opinião alternativa sobre a conveniência de usar exatamente modelos AR para estimativa espectral, embora de ordem superior.
4. Para processos muito curtos e não estacionários, em vez da matriz de estimativas da função de autocorrelação, a matriz de covariância é geralmente usada em (3).
5. Para um estudo detalhado da questão da estimativa espectral autoregressiva, S.L. Marple ml. "Análise espectral digital e suas aplicações", M., Mir, 1990