
Na comunidade científica, a visualização de dados e o design da teoria desempenham um papel muito importante. Ferramentas que implementam comandos do LaTeX , como Markdown e MathJax, são frequentemente usadas para uma apresentação conveniente e bonita de fórmulas.
Para Julia, há também um conjunto de pacotes que permitem usar a sintaxe do LaTeX e, em conjunto com os meios da álgebra simbólica, obtemos uma ferramenta poderosa para lidar com fórmulas.
Baixe e conecte tudo o que você precisa hoje
using Pkg Pkg.add("Latexify") Pkg.add("LaTeXStrings") Pkg.add("SymEngine") using Latexify, LaTeXStrings, Plots, SymEngine
LaTeXStrings
LaTeXStrings é um pequeno pacote que facilita a inserção de equações de LaTeX em literais de string de Julia. Ao usar cadeias regulares em Julia para inserir uma literal de cadeia com equações do LaTeX incorporadas, você deve evitar manualmente todas as barras invertidas e cifrões: por exemplo, $ \alpha^2 $ é gravado \$\\alpha^2\$ . Além disso, embora o IJulia seja capaz de exibir equações no formato LaTeX (via MathJax ), isso não funcionará com linhas regulares. Portanto, o pacote LaTeXStrings define:
- A classe
LaTeXString (um subtipo de String ) que funciona como uma string (para indexação, conversão etc.), mas é automaticamente exibida como texto / látex no IJulia. - Macros de seqüência de caracteres
L"..." e L"""...""" que permitem inserir equações do LaTeX sem escapar de barras invertidas e cifrões (e que adicionam cifrões para você, se você os omitir).
S = L"1 + \alpha^2"
O REPL produzirá :
"\$1 + \\alpha^2\$"
e Jupyter exibirá:
1+ alpha2
A indexação funciona como linhas normais:
S[4:7] "+ \\a"
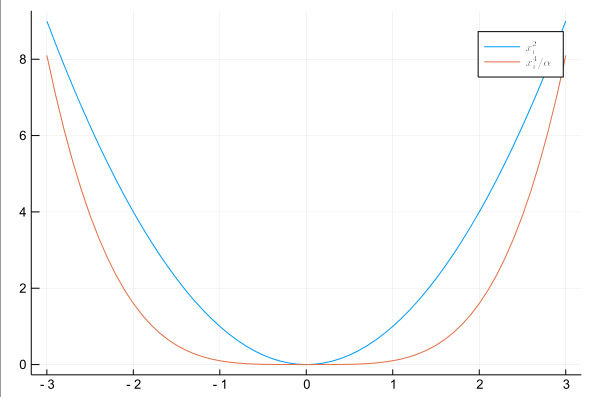
Tais linhas podem ser úteis no design de gráficos.
x = [-3:0.1:3...] y1 = x .^2 α = 10 y2 = x .^4 / α; plot(x,y1, lab = "\$x^2_i\$") plot!(x,y2, lab = L"x^4_i/\alpha")
Latexify
Um pacote mais funcional é o Latexify ( Guia ). Ele foi projetado para gerar matemática LaTeX a partir de objetos julia. Este pacote usa a homologia de Julia para converter expressões em strings no formato LaTeX. O Latexify.jl fornece funções para converter vários objetos Julia diferentes, incluindo:
- Expressões
- Cordas
- Números (incluindo racionais e complexos),
- Expressões simbólicas de SymEngine.jl,
- ParameterizedFunctions e ReactionNetworks from DifferentialEquations.jl
bem como matrizes de todos os tipos suportados.
ex = :(x/(y+x)^2)
fracx left(y+x right)2
str = "x/(2*k_1+x^2)"
fracx2 cdotk1+x2
Matriz de elementos heterogêneos:
m = [2//3 "e^(-c*t)" 1+3im; :(x/(x+k_1)) "gamma(n)" :(log10(x))] latexify(m)
\ left [\ begin {array} {ccc} \ frac {2} {3} & e ^ {- c \ cdot t} e 1 + 3 \ textit {i} \\ \ frac {x} {x + k_ {1}} & \ Gamma \ left (n \ right) e \ log_ {10} \ left (x \ right) \\ \ end {array} \ right]
Você pode especificar uma função que exiba fórmulas e as copie para o buffer no formato compreensível para Habr:
function habr(formula) l = latexify(formula) res = "\$\$display\$$l\$display\$\$\n" clipboard(res) return l end habr(ex)
fracx left(y+x right)2
<p>$<!-- math>$$display$$\frac{x}{\left( y + x \right)^{2}}$$display$$</math -->$</p>
Tenha em mente
latexify("x/y") |> display
fracxy
latexify("x/y") |> print
$\frac{x}{y}$
Symengine
SymEngine é um pacote que fornece cálculos simbólicos que você pode visualizar no seu Jupyter com Latexify.
Você pode especificar caracteres em linhas e aspas ( quote ):
julia> a=symbols(:a); b=symbols(:b) b julia> a,b = symbols("ab") (a, b) julia> @vars ab (a, b)
Defina a matriz e exiba-a lindamente
u = [symbols("u_$i$j") for i in 1:3, j in 1:3] 3×3 Array{Basic,2}: u_11 u_12 u_13 u_21 u_22 u_23 u_31 u_32 u_33 u |> habr
\ left [\ begin {array} {ccc} u_ {11} e u_ {12} e u_ {13} \\ u_ {21} e u_ {22} e u_ {22} e u_ {23} \\ u_ {31} e u_ {32} & u_ {33} \\ \ end {array} \ right]
Suponha que temos vetores
C = symbols("Ω_b/Ω_l") J = [symbols("J_$i") for i in ['x','y','z'] ] h = [0, 0, symbols("h_z")] 3-element Array{Basic,1}: 0 0 h_z
que deve ser multiplicado por vetores
using LinearAlgebra × = cross latexify(J×h, transpose = true)
exibição $$ $$ \ begin {equação} \ left [\ begin {array} {c} J_ {y} \ cdot h_ {z} \\ - J_ {x} \ cdot h_ {z} \\ 0 \\ \ fim {array} \ right] \ fim {equação} $$ display $$
Cálculos de matriz completa:
dJ = C*(u*J.^3)×h latexify( dJ, transpose = true) habr(ans)
exibição $$ $$ \ begin {equação} \ left [\ begin {array} {c} \ frac {h_ {z} \ cdot \ left (u_ {21} \ cdot J_ {x} ^ {3} + u_ { 22} \ cdot J_ {y} ^ {3} + u_ {23} \ cdot J_ {z} ^ {3} \ right) \ cdot \ Omega_ {b}} {\ Omega_ {l}} \\ \ frac { - h_ {z} \ cdot \ left (u_ {11} \ cdot J_ {x} ^ {3} + u_ {12} \ cdot J_ {y} ^ {3} + u_ {13} \ cdot J_ {z} ^ {3} \ right) \ cdot \ Omega_ {b}} {\ Omega_ {l}} \\ 0 \\ \ end {array} \ right] \ end {equação} $$ display $$
mas com uma corrente tão simples, você pode encontrar o determinante e enviá-lo para Habr
u |> det |> habr
u11 cdot left(u22− fracu12 cdotu21u11 right) cdot left(u33− fracu13 cdotu31u11− frac left(u23− fracu13 cdotu21u11 right) cdot left(u32− fracu12 cdotu31u11 right)u22− fracu12 cdotu21u11 right)
Recursivo! A matriz inversa é provavelmente calculada de maneira semelhante:
u^-1 |> habr
Spoiler$$ display $$ \ left [\ begin {array} {ccc} \ frac {1 - \ frac {u_ {12} \ cdot \ left (\ frac {- u_ {21}} {u_ {11}} - \ frac {\ left (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31 }} {u_ {11}} \ right)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) } \ right) \ cdot \ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right)} {u_ {33} - \ frac {u_ {13 } \ cdot {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ { 21}} {u_ {11}}}} à direita)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} - \ frac {u_ {13} \ cdot \ left (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31 }} {u_ {11}} \ right)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) } \ right)} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u _ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}}} {u_ {11}} & \ frac {\ frac {- u_ {12} \ cdot \ left (1 + \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {\ left (u_ {22 } - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} { u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} } \ right)} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} + \ frac {u_ {13} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {\ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21} } {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23 } - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} { u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ rig ht)}} {u_ {11}} & \ frac {\ frac {- u_ {13}} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12 } \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}} + \ frac { u_ {12} \ cdot \ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right)} {\ left (u_ {22} - \ frac { u_ {12} \ cdot u_ {21}} {u_ {11}} \ direita) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ { 12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right)} } {u_ {11}} \\ \ frac {\ frac {- u_ {21}} {u_ {11}} - \ frac {\ left (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ direita)} \ direita) \ cdot \ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right)} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ { 12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}}} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} & \ frac {1 + \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} { \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right)}} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} & \ frac {- \ left (u_ {23 } - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right)} {\ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} { u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ direita) \ cdot \ left (u_ {32} - \ frac { u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right )} \\ frac {\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ direita)}} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} { u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}} & \ frac {- \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {\ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21 }} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right)} & \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} { u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ c ponto \ esquerda (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ direita)} {u_ {22} - \ frac {u_ {12} \ cdot u_ { 21}} {u_ {11}}} \ right) ^ {- 1} \\ \ end {array} \ right] $$ display $$
Se você quiser prejudicar o Matjax, coloque menos o segundo grau (o quadrado da matriz inversa)
A propósito, o SymEngine considera derivativos:
dJ[1] |> habr
frachz cdot left(u21 cdotJ3x+u22 cdotJ3y+u23 cdotJ3z right) cdot Omegab Omegal
diff(dJ[1], J[1]) |> habr
frac3 cdotJ2x cdothz cdotu21 cdot Omegab Omegal
A propósito, Julia pode usar não apenas fórmulas, mas também gráficos do LaTeX 'a. E se você instalou o MikTex e já baixou pgfplots , usando o ambiente apropriado, você pode fazer amizade com Julia, que fornecerá a oportunidade de criar histogramas, gráficos tridimensionais, erros e relevos com contornos e depois integrá-lo ao documento LaTeX.
Isso é tudo com fórmulas, mas não com cálculos simbólicos: Julia ainda tem soluções mais complexas e interessantes para álgebra simbólica, com as quais iremos lidar definitivamente na próxima vez.