Sobre a proximidade dos picos

“Antes de você entender isso, parece um milagre. Mas depois disso não há nada de especial. ”

Não, não sobre montanhas, - sobre contagens. Em matemática, existem perguntas cuja formulação é acessível a todos, mas a solução é não trivial e sem preparação especial é difícil de explicar. Um desses problemas pode ser expresso brevemente da seguinte maneira: como calcular corretamente as distâncias em gráficos direcionados? Esse problema um tanto abstrato pode ser reduzido a uma tarefa motivadora muito específica. Cabe em uma imagem:

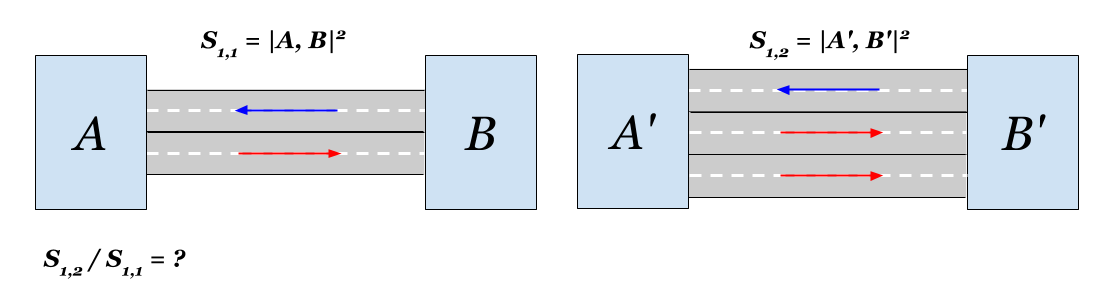
1. Declaração do problema. Eu moro em um, mas você no outro.

Uma cidade pequena é dividida (por exemplo, por um rio, embora no contexto dos picos o desfiladeiro seja mais adequado) em dois distritos (partes) $$$A$ e $$$B$ . A comunicação entre os distritos é realizada ao longo de uma única estrada (ponte), que possui duas faixas: ao lado da $$$A$ para $$$B$ e vice-versa. Em conexão com o crescimento populacional, surgiu a questão de aumentar a capacidade da estrada. O dinheiro, como sempre, mal é suficiente e apenas o suficiente para uma faixa em uma direção. É claro que mesmo uma faixa aproxima as regiões, mas a questão é quanto exatamente? Você é um matemático louco urbano, e foi você quem foi convidado para receber uma resposta razoável .

Qual a distância entre as áreas se você construir outra faixa em uma direção?

Redação para avançado

Em vez de pontes de Konigsberg , uma linguagem de teoria de grafos um pouco mais rigorosa pode ser usada. Portanto, há um gráfico direcionado com dois vértices (nós) $$$A$ e $$$B$ . A magnitude da conexão (condutividade, largura de banda) na direção direta e reversa é inicialmente igual. A questão é: quanto a distância entre os nós mudará se a condutividade em uma das direções dobrar?

E sim, se você é realmente um soldador matemático, pode oferecer (e justificar) uma solução para quaisquer valores diretos e de feedback. Idealmente, para um gráfico com qualquer número de nós e links.

Intimidade e andanças bêbadas

É claro que a distância usual (km) entre as regiões não depende da presença ou ausência da estrada. Portanto, não se encaixa aqui - precisamos confiar na comunicação. Quanto mais distritos estiverem conectados - quanto mais próximos eles estiverem - mais residentes poderão chegar a outra área por unidade de tempo.

Para avaliar a medida da proximidade entre os nós de um gráfico não direcionado, pode-se usar a chamada distância resistiva . Anteriormente, já descrevemos as propriedades dessa distância no habr em vários artigos .

A distância resistiva é equivalente ao conceito de resistência efetiva, quando se trata da rede elétrica. Portanto, na linguagem elétrica, o problema pode ser formulado da seguinte maneira. Entre dois nós, dois diodos de condutividades iguais são conectados no sentido anti-horário. Como a resistência entre esses pontos muda se você adicionar outro diodo? (Peço desculpas se a linguagem elétrica falhou e escrevi bobagens aqui).

Além disso, a resistência efetiva pode ser interpretada na linguagem Markov pelas probabilidades de passeios aleatórios bêbados (para aqueles que desejam se aprofundar no tópico - google “Passeios aleatórios e redes elétricas”).

A distância resistiva é quadrática, - corresponde ao quadrado da distância linear. As distâncias quadráticas também são chamadas de quadrans . Mas como outras distâncias (lineares) não são usadas neste problema, não precisamos do termo quadrans aqui. (Existe língua de pássaro suficiente mesmo sem ela).

Em geral, o termo "distância resistiva" também não parece bom. Ele implica que estamos falando de algum tipo de distância incomum desconhecida pela ciência. De fato, a distância resistiva é a distância euclidiana usual. Mas no espaço afim. Nós usamos esse recurso ainda mais.

E qual é, de fato, o problema?

Se sabemos o que é uma "distância resistiva", por que não podemos "apenas pegar e calcular" para um determinado gráfico?

Hum. Em princípio, fácil. Se estamos falando de um gráfico não direcionado. Se a cidade tivesse construído faixas nas duas direções, a distância resistiva teria diminuído exatamente pela metade. Como a resistência é inversamente proporcional à condutividade, a condutividade (taxa de transferência) dobrou. E se eu adicionasse duas bandas em cada direção, a distância diminuiria 3 vezes. Tudo é bastante trivial aqui. (E provavelmente alguém aqui já pode adivinhar a forma geral da solução. E vamos mais longe).

Quando os relacionamentos opostos não são iguais, tudo se complica. E muito severamente.

Não existe uma maneira legal e geralmente aceita de determinar a proximidade de picos (distâncias resistivas) em um gráfico direcional .

(Esta é minha tese - talvez alguém possa me convencer). “Não” - aqui significa que não está nos livros didáticos, no wiki e na cabeça (mais precisamente - existem muitas maneiras diferentes de diferentes autores que exigem diferentes suposições e definições). Existe um caminho (embora não seja tão simples). Neste artigo, estamos apenas descrevendo-o.

A própria determinação da distância na presença de conexões direcionadas requer esclarecimentos se estamos falando de um gráfico direcionado (métrica não comutativa, peço desculpas). Você pode falar sobre a distância de $$$A$ antes $$$B$ , mas você pode $$$B$ antes $$$A$ . E provavelmente essas distâncias nem sempre são iguais. De que tipo de distâncias estamos falando no problema?

Regras de distância euclidiana

Vamos emergir e respirar fundo. Já mencionamos que a distância resistiva é o euclidiano usual. Isso significa que sua definição pode ser reduzida à definição de distância euclidiana como a norma da diferença de dois elementos:

$$$S (A, B) = | A - B | ^ 2 = (A - B) ^ 2 = (A - B) \ cdot (A - B) = S (B, A) \ quad (1)$

Essa definição não depende da ordem dos elementos - esta é a distância comutativa, a proximidade (mais precisamente, a distância) dos elementos. Um ponto em uma expressão significa uma operação escalar do produto (espaço métrico). Por conseguinte, a expressão (1) pode ser divulgada:

$$$S (A, B) = S (B, A) = A ^ 2 + B ^ 2 - A \ cdot B - B \ cdot A \ quad (2)$

Aqui $$$A ^ 2 = A \ cdot A$ , $$$B ^ 2 = B \ cdot B$ - normas de elementos. Quando se trata de gráficos, as normas dos elementos geralmente são zero. No problema original, nada é dito sobre as normas, para que você possa considerá-las nulas (mais sobre o significado das normas dos elementos no espaço afim. Aqui , e ainda mais detalhes, aqui ). Então a expressão para a distância desejada assume a forma:

$$$S (A, B) = - (A \ cdot B + B \ cdot A) = s_ {AB} + s_ {BA} \ quad (3)$

De acordo com a expressão (3), tudo o que é necessário para resolver o problema é encontrar os produtos escalares dos elementos (nós) em um gráfico direcionado (é fácil dizer, mas como fazer isso?).

Ao longo do caminho, a fórmula (3) mostra que nossa medida geral (comutativa) de proximidade entre elementos $$$A$ e $$$B$ é a soma de duas distâncias direcionadas:

$$$s_ {AB} = - A \ cdot B$ - distância direcional de $$$A$ antes $$$B$ ,
$$$s_ {BA} = - B \ cdot A$ - distância direcional de $$$B$ antes $$$A$ .

2. A decisão. Longo caminho nas dunas

O estrondo diminuiu. A diversão acabou. Em seguida, vêm os detalhes sem graça da descrição da essência do método para calcular o produto escalar entre os nós de um gráfico direcionado. Esta é a parte que eu não sei dizer "de uma maneira simples nos dedos". Mas é aí que a coisa mais importante no artigo. Algo que vale a pena perder tempo com isso.

A linha geral de raciocínio é a seguinte. Com cuidado e sem emoções de novas suposições adicionais, transferimos as propriedades conhecidas da métrica dos espaços simétricos para as assimétricas. Tudo o que é necessário é levar em consideração os recursos da métrica em espaços afins.

Qualquer gráfico conectado (direcionado ou não) define um espaço métrico afim. Algumas propriedades de tais espaços na execução simétrica (comutativa) foram (caoticamente) descritas na série de artigos já mencionada ou mais precisamente e em detalhes na longrid mencionada. Não se apresse em mudar - abaixo, damos (pelo trava-língua) os principais apertos.

Afinar espaço métrico (gráfico não direcionado)

O que é importante. Bem conhecido primeiro.

1. A afinidade do espaço significa que os conceitos de vetor e elemento no espaço são diferentes. Vetor é a diferença de elementos. Esse recurso aparentemente insignificante leva a consequências significativas se uma métrica for definida no espaço.

2. O espaço é definido por uma base composta por elementos. Os vértices do gráfico são a base do espaço. Os relacionamentos em um gráfico determinam suas propriedades de métricas.

3. Uma característica de conectividade do gráfico é a matriz de adjacência . Mas para propriedades métricas (e outras), o Laplaciano do gráfico (matriz de Kirchhoff) é mais importante $$$L$ .

4. O Laplaciano de um gráfico é um tensor quase métrico. "Quase" - aqui significa que está incompleto. Laplaciano é uma matriz degenerada e, portanto, não invertível. E o tensor métrico padrão é completamente reversível.

Agora menos conhecido.

5. A diferença entre elementos e vetores em um espaço métrico afim leva à existência de um vetor nulo nele $$$\ mathbb z$ . O produto escalar de elementos com um vetor nulo em um espaço comutativo (simétrico) é igual a unidade (em um espaço não comutativo, depende da direção da multiplicação). Sem um vetor zero, o espaço do gráfico não está completo! Isso é importante.

6. O centro ortogonal da base é duplo em relação ao vetor nulo. $$$Z$ . Esse é um elemento ortogonal a todos os outros elementos da base (exceto o vetor zero). Lembre-se de que a ortogonalidade dos elementos significa que seu produto escalar é zero. O ortocentro de um triângulo é o círculo circunscrito . Sim, em um espaço afim completo, um elemento com uma norma diferente de zero não é um ponto, mas uma esfera n-dimensional.

7. O Laplaciano do gráfico, juntamente com as coordenadas do centro ortogonal, fica completo (um tensor métrico completo). Em outras palavras, laplaciano completo $$$Lm$ É um conde ordinário laplaciano $$$L$ mas delimitada pelas coordenadas baricêntricas do centro ortogonal.

8. A inversão do Laplaciano completo permite obter um Gramian completo $$$Gm$ - a matriz de produtos escalares dos elementos da base (no nosso caso, os vértices do gráfico). Esse gramiano também é um tensor métrico de espaço completo.

9. O enquadramento de um gramiano completo é uma tupla de unidades (produtos escalares de elementos de base e um vetor zero). No canto - zero, esta é a norma do próprio vetor zero.
A famosa matriz de Cayley-Menger é um gramiano quase regular.

Como resultado, concluímos que, de acordo com a reivindicação 8, o problema de determinar produtos escalares (e, portanto, distâncias) entre os nós do gráfico é reduzido para determinar o tensor métrico inicial da base. $$$Gm$ .

Precisamos de um método para construir um gráfico gramiano completo $$$Gm$ para um dado Laplaciano (incompleto) $$$L$ .

No caso de ligações simétricas, a construção de um Gramiano completo a partir do Laplaciano (e vice-versa) não causa dificuldades particulares. Nesse caso, os produtos escalares dos elementos da base e o vetor zero são comutativos - eles não dependem da ordem de multiplicação:

$$$\ mathbb z \ cdot A = A \ cdot \ mathbb z = 1$

Para gráficos direcionados (espaços não comutativos), o problema é complicado. Se apenas porque o número muito possível de conexões no gráfico direcionado dobra.

Espaço afim não comutativo (gráfico direcionado)

Sobre as propriedades do Laplaciano do gráfico direcionado, também já escrevemos no Habr . Eles disseram como usar os potenciais do Laplaciano para classificar objetos. Em termos de bases, os potenciais do Laplaciano são as coordenadas duplas do vetor zero (aniquilador do Laplaciano).

Neste artigo, estamos interessados ​​em propriedades de métricas. Se o gráfico for direcionado, o produto escalar entre seus vértices depende da ordem:

$$$A \ cdot B \ ne B \ cdot A$

Isso significa que as coordenadas duplas nos gráficos direcionados são divididas (em esquerda e direita). Os valores dos produtos escalares do vetor zero e os elementos da base (na fronteira com o gramiano) também dependem da ordem dos fatores. E, portanto, em contraste com o espaço comutativo, aqui a metade das coordenadas duplas do vetor zero é desconhecida e deve ser determinada.

$$$\ mathbb z \ cdot A \ ne A \ cdot \ mathbb z$

No entanto, existem muitas quantidades conhecidas.

Em primeiro lugar, o próprio Laplaciano é conhecido. Além disso, sabe-se que a soma de suas linhas é zero (no caso geral, esse é um requisito opcional, mas para os laplacianos de gráficos direcionados geralmente é assim). Também é importante que as coordenadas baricêntricas dos elementos sejam únicas, pois são independentes da métrica espacial. Ou seja, a fronteira do Laplaciano do gráfico é simétrica, tanto para o gráfico direcionado quanto para o não direcionado (não reconheci imediatamente esse ponto). Por fim, conhecemos as normas dos elementos da base (geralmente nos gráficos são iguais a zero).

Resta substituir todo o conhecido e desconhecido na identidade que liga o Laplaciano e o Gramiano:

$$$Lm \ Gm = I$

Aqui $$$I$ É uma matriz de identidade. Nesta identidade, o significado da transição de um Laplaciano incompleto para um completo.

Cale a boca e acredite

Vamos passar de palavras para ações. É assim que o Laplaciano se parece $$$L$ para um gráfico de dois nós:

$$$L = \ begin {bmatrix} c_1 & -c_1 \\ c_2 & -c_2 \ end {bmatrix}$

Para simplificar, designamos o relacionamento com números: $$$c_1 = c_ {AB}, c_2 = c_ {BA}$ . Supõe-se que os valores dos títulos sejam conhecidos - através deles expressaremos todas as outras quantidades.

Laplaciano completo $$$Lm$ inclui as coordenadas do ortocentro $$$[rz, az, bz]$ :

$$$Lm = \ begin {bmatrix} rz e az & bz \\ az & c_1 & -c_1 \\ bz & c_2 & -c_2 \ end {bmatrix}$

Aqui $$$rz$ - a norma do ortocentro (no caso simétrico é interpretado como o quadrado do raio), $$$az$ e $$$bz$ - coeficientes de decomposição do ortocentro com base $$$A, B$ (pesos baricêntricos).

Gramiano completo $$$Gm$ Parece algo como isto:

$$$Gm = \ begin {bmatrix} 0 & za & zb \\ 1 & 0 & g_1 \\ 1 & g_2 & 0 \ end {bmatrix}$

Aqui estão as tuplas $$$[za, zb]$ e $$$[1, 1]$ refletem as coordenadas duplas do vetor nulo. Essas coordenadas são aniquiladoras do Laplaciano (quando multiplicadas pelo Laplaciano, elas dão um vetor zero - não devem ser confundidas com um vetor zero!).

Para resolver o problema, precisamos encontrar a soma dos valores do gramiano: $$$- (g_1 + g_2)$ .

Consideramos o número de incógnitas: $$$rz, az, bz, za, zb, g_1, g_2$ - apenas 7 (sim, sim - para descobrir o valor de uma distância infeliz, precisamos calcular mais sete valores adicionais). Existem duas conexões bem conhecidas na entrada - $$$c_1$ e $$$c_2$ . Identidade $$$Lm \ Gm = I$ dará 9 equações. Total 7 + 2 = 9, - tudo converge (surpreendentemente). Resta simplesmente resolver o sistema de equações.

Para um gráfico de dois nós, a solução (todas as incógnitas) pode ser expressa de forma explícita. Damos expressões finitas para as quantidades de interesse para nós. Introduzimos o conceito de conectividade geométrica geral - esse é o recíproco da norma do centro ortogonal $$$gc = 1 / rz$ . Sua dimensão coincide com a dimensão dos links do gráfico. Para um gráfico de dois nós (e duas conexões), a conexão geométrica tem uma bela expressão:

$$$gc = 1 / rz = (\ sqrt {c_1} + \ sqrt {c_2}) ^ 2$

Por meio dessa conexão, é possível expressar produtos escalares de nós:

$$$g_1 = -gc \ sqrt {c_2}, \ quad g_2 = -gc \ sqrt {c_1}$

Você pode traduzir produtos escalares $$$g$ em distâncias direcionais $$$s$ (3)

$$$s_ {BA} = gc \ sqrt {c_ {AB}}; \ quad s_ {BA} = gc \ sqrt {c_ {AB}}$

A distância comutativa desejada entre nós é determinada pela soma:

$$$S (A, B) = s_ {BA} + s_ {AB} = 1 / \ sqrt {c_ {AB} c_ {BA}} \ quad (4)$

Vovó chegou

Finalmente. Expressão (4) - esta é a fórmula desejada.

A distância entre os vértices do gráfico de dois nós é inversamente proporcional à raiz quadrada do produto dos contra-links.

Você pode carregar o livro escolar com outra fórmula inútil.

Se as conexões forem iguais, o resultado coincidirá com a distância resistiva nos gráficos não direcionados:

$$$S_ {c, c} (A, B) = 1 / c \ quad (4.1)$

Vamos calcular o que há com a nossa cidade. Se você colocar uma segunda faixa, a comunicação em uma direção duplicará. Assim, a nova distância $$$S_ {1, 2} (A, B)$ pode ser expresso em termos do original:

$$$S_ {1, 2} (A, B) = 1 / \ sqrt {2 c_ {AB} c_ {BA}} = 1 / \ sqrt {2} S_ {1, 1} (A, B)$

A distância entre as áreas diminuirá em $$$\ sqrt {2}$ vezes. Era óbvio, certo?

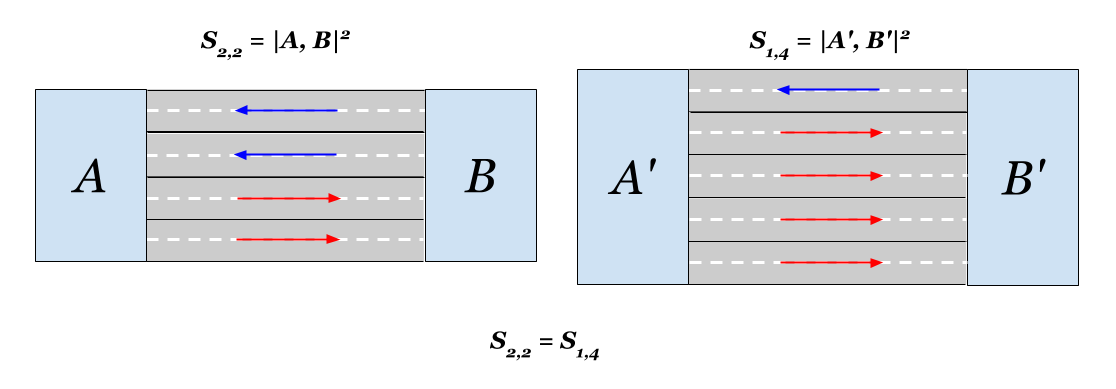
Acontece também que, em termos de distância, adicionar uma faixa a cada estrada de duas faixas de cada lado equivale a adicionar três faixas de um lado. A proximidade euclidiana em ambos os casos dobrará. Interessante.



Só isso. Obrigado pela atenção).