Na matemática, onde a prova é tudo, os fatos também são importantes. No entanto, os fatos são bons, apenas enquanto o modelo é bom e a construção de modelos é uma ocupação não confiável. Então, quantos fatos serão suficientes?

Você pode encontrar o próximo número na sequência?
1, 2, 4, 8
Aqui está mais um número, se você precisar de mais dados para tomar uma decisão:
1, 2, 4, 8, 16
O próximo número deve ser 32, certo? O padrão é claro: para encontrar o próximo número, você precisa dobrar o número anterior. 1 × 2 = 2; 2 × 2 = 4; 4 × 2 = 8; 8 × 2 = 16. Portanto, o próximo número deve ser 16 × 2 = 32. Quantos fatos a mais são necessários para confirmar isso?
Mas, embora seja razoável supor que o próximo número seja 32, isso nem sempre será verdadeiro. Considere a seguinte sequência: contaremos o número de seções nas quais o círculo é dividido por linhas que conectam pontos localizados em um círculo.
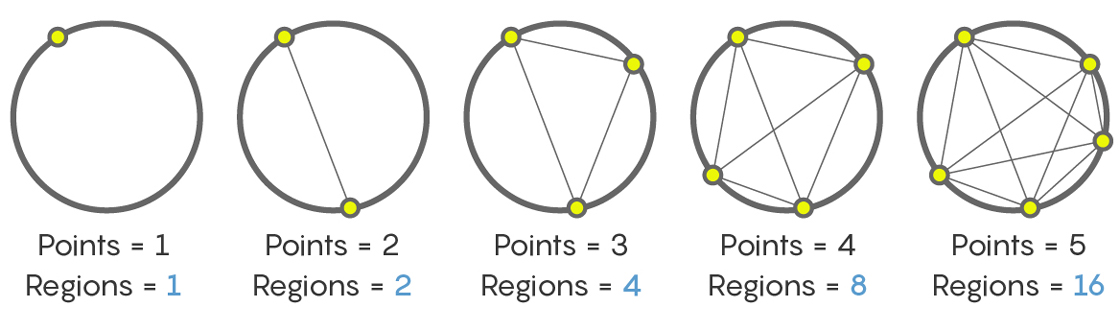
Um ponto fornece uma seção (toda a parte interna do círculo). Dois pontos - duas seções. Três pontos - quatro seções. Cinco e seis são oito e dezesseis, respectivamente. O resultado é uma sequência
1, 2, 4, 8, 16
E quantas seções aparecerão depois de conectar as linhas de seis pontos no círculo? Ninguém o condenará se você, como muitas pessoas que se deparam com essa tarefa pela primeira vez, disser isso 32. Mas não é assim. De fato, não importa quão irritante, a resposta será - 31! Reconte-se e verifique novamente.
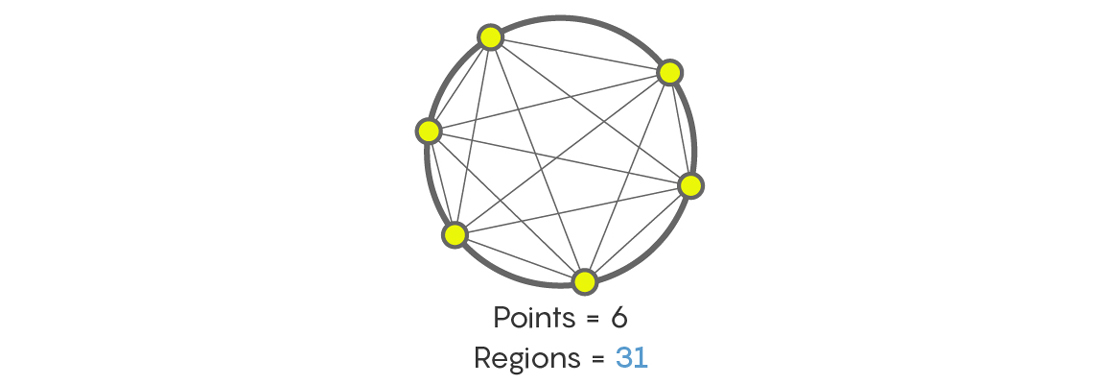
Obviamente, existem seqüências como 1, 2, 4, 8, 16, 32, 64 e assim por diante, a partir de números dobrando a cada vez. Mas existem outras seqüências, por exemplo, o número máximo de seções nas quais o círculo é dividido por linhas que conectam os pontos no círculo, e isso é 1, 2, 4, 8, 16, 31, 57, 99 e assim por diante. Atendendo à sequência 1, 2, 4, 8, 16, podemos pensar que todos os fatos são que o próximo número será 32, mas pode haver algo mais.
A matemática tem uma longa tradição de desafiar nossas expectativas e fazer nossa imaginação funcionar. Portanto, os matemáticos sempre se esforçam para obter provas rigorosas, não apenas fatos. A prova estabelece a verdade matemática. Todos os fatos podem apontar 32 como o próximo número em nossa sequência, mas sem provas rigorosas, não podemos ter certeza disso.
Mas, ainda assim, os fatos para os matemáticos são úteis e importantes. Antes de provar algo, costumamos brincar com as informações disponíveis, estudar o problema, considerar exemplos e coletar dados. Estudamos e ponderamos os fatos e decidimos o que fazer a seguir. Esses resultados formam nossa opinião, propondo provar alguns teoremas e refutar outros.
A hipótese de gêmeos primos é um exemplo em que os fatos controlam nosso pensamento matemático da mesma maneira que a prova. Os números primos gêmeos são pares de números primos que diferem em 2 - por exemplo, 3 e 5, 11 e 13, 101 e 103. A hipótese de números primos gêmeos sugere que não há um par maior de gêmeos - ou seja, semelhante pares aparecem constantemente na linha numérica quando se move para o infinito.
A hipótese de gêmeos primos não é um teorema, porque, apesar de ser um dos problemas mais famosos da teoria dos números, ninguém ainda conseguiu provar isso. No entanto, quase todo mundo acredita que isso é verdade, pois há muitos fatos em seu apoio.
Por exemplo, em nossa busca por números primos, encontramos constantemente pares extremamente grandes de números primos gêmeos. Cada um dos números primos do maior
par conhecido hoje contém 400.000 dígitos. Teoremas semelhantes a esta hipótese também são comprovados. Em 2013,
Zhang Ethan chocou a comunidade matemática ao provar a presença de um número infinitamente grande de pares de números primos, diferindo em não mais de 70 milhões. Graças ao projeto aberto
Polymath que se seguiu, sabemos que há um número infinito de pares de números primos que diferem em
não mais que 246 . Ainda não provamos a existência de um número infinito de pares de números primos que diferem em 2 - mas ainda assim 2 está muito mais próximo de 246 do que 246 do infinito.
Por essas e outras razões, a crença na justiça, mesmo que a hipótese não seja comprovada, não é muito controversa. No entanto, existem outras áreas da matemática nas quais os fatos são usados para criar opiniões informadas que são mais controversas.
No estudo das curvas elípticas, sua classificação, grosso modo, denota uma estimativa numérica da complexidade de resolver essa curva. Por muitos anos, acreditava-se que as
fileiras das curvas elípticas não são limitadas , ou seja, não há restrições quanto ao valor da classificação da curva ou à complexidade da solução.
No entanto, trabalhos recentes fazem com que os matemáticos pensem na possibilidade de classificação limitada. O artigo apresenta fatos indicando que é possível que exista um número finito de curvas cuja classificação seja maior que 21.
No entanto, recomenda-se cautela. Os fatos coletados pelos matemáticos não são retirados do mundo das curvas elípticas - eles se relacionam com as matrizes que os pesquisadores usaram para modelar as curvas. Os modelos matemáticos são amplamente utilizados na ciência e podem até ser virados para dentro para estudar a própria matemática. Essas são ferramentas incrivelmente poderosas que permitem substituir uma tarefa incompreensível por uma tarefa mais fácil de lidar.
Mas usar modelos é um negócio complicado. Você nunca pode ter certeza de que o modelo se comporta de maneira bastante semelhante ao que estamos tentando entender, para que possamos tirar conclusões de seu comportamento. Além disso, não se pode ter certeza de que nosso modelo seja semelhante precisamente em locais de maior importância. Portanto, é difícil garantir que os fatos que coletamos com base em modelos realmente testemunhem as propriedades reais dos fenômenos que estamos estudando. Vamos examinar esses problemas com base em um modelo simples de uma hipótese simples.
Imagine que queremos estudar a seguinte afirmação: quaisquer duas linhas são cruzadas ou paralelas.
Por interseção, queremos dizer a presença de linhas retas em pontos comuns, e pelo paralelismo o fato de que elas seguem uma direção, mas não se cruzam (esse conceito pode ser definido de maneira diferente, mas usarei isso por simplicidade).
Para estudar esse problema, crie um modelo. Cada linha é representada pela equação da linha oblíqua, que você pode lembrar do curso da escola. Ou seja, assumimos que cada linha pode ser descrita por uma equação da forma
y = mx + b
onde m é a inclinação da linha (sua inclinação) eb é o ponto de interseção do eixo y (eixo vertical).
Modelar linhas dessa maneira é conveniente para experimentos nelas. O modelo nos permite criar uma linha aleatória selecionando um par de números aleatórios, m e b. Podemos selecionar um par de linhas aleatórias e verificá-las - elas se cruzam? Eles seguem um caminho? Algo está acontecendo?
Aqui estão alguns exemplos de como os resultados dessas experiências podem parecer.
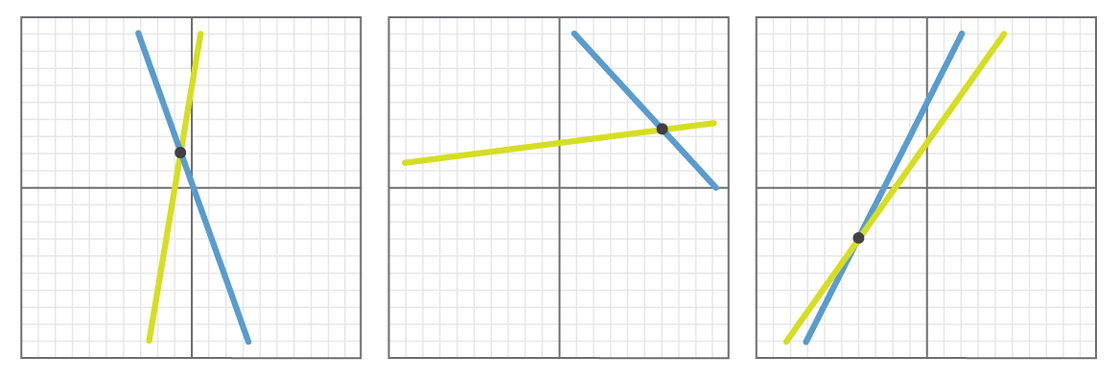
Em cada exemplo, as linhas selecionadas aleatoriamente se cruzam. Se realizarmos esse experimento mil vezes - ou 10.000, ou um milhão -, descobriremos que em todos os casos as linhas se cruzarão ou serão paralelas (e provavelmente todas as linhas se cruzarão, pois é improvável que as duas linhas tenham a mesma inclinação, escolhida por acaso).
Portanto, olhando para um milhão de exemplos, você pode concluir que a hipótese é provavelmente verdadeira. Todos os fatos sustentam totalmente a afirmação de que qualquer par de linhas é paralelo ou se cruza.
No entanto, os fatos são tão bons quanto o modelo e a modelagem é perigosa. Vamos ver quais perigos criamos para nós mesmos em nosso exemplo.
Um problema é que certos tipos de linhas serão mais comuns que outros. Aqui está um gráfico mostrando 50 linhas com b = 0 e 0 ≤ m ≤ 1.
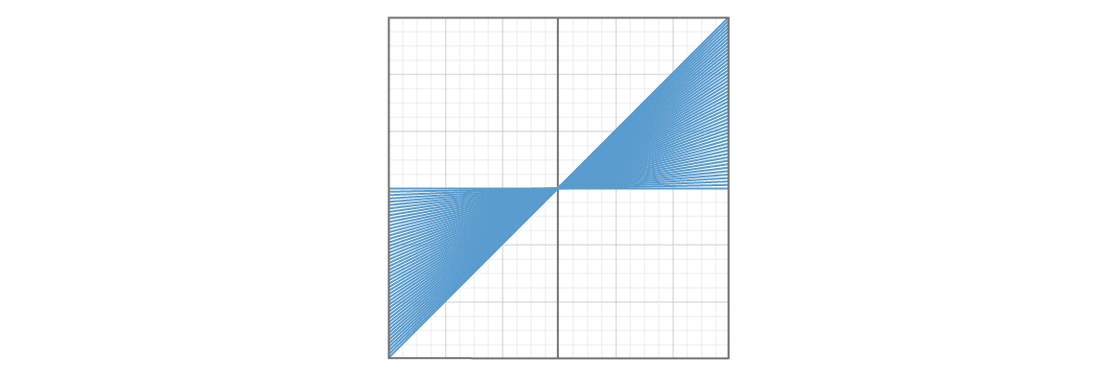
E aqui está um gráfico mostrando 50 linhas com b = 0 e m ≥ 1.

Parece que um quarto do avião é coberto por linhas retas com uma inclinação de 0 a 1, e outro quarto é coberto por linhas retas com uma inclinação maior que 1. Escolher um número maior que 1 parece mais provável do que escolher um número de 0 a 1; portanto, é mais provável que uma linha reta estará na segunda seção do avião. Isso significa que certas linhas, com uma inclinação de 0 a 1, serão extremamente pouco representadas no modelo. E se algumas coisas estranhas acontecem nesta parte do avião com linhas retas, é improvável que nosso modelo nos conte sobre isso.
Se você olhar atentamente para o segundo gráfico, veremos outro problema. Quanto maior o m, maior a inclinação das linhas retas. A linha reta mais legal é vertical. Qual é a inclinação da linha vertical? Por definição, não está definido: não existe um número m que possa descrever a linha vertical. Acontece que não há linha vertical em nosso modelo e não podemos fazer experiências com ela. Ainda não começamos a coletar fatos, mas já descartamos alguns casos especiais simplesmente por causa do esquema de construção do modelo.
O mesmo diz respeito ao problema mais sério do nosso modelo. Pessoas que imaginam facilmente o espaço tridimensional provavelmente notaram imediatamente que nossa hipótese está errada. Uma linha reta não precisa se cruzar ou ser paralela. Imagine dois corredores indo em direções diferentes em diferentes andares de um edifício. São linhas retas que se cruzam - linhas retas que não se cruzam e não são paralelas.
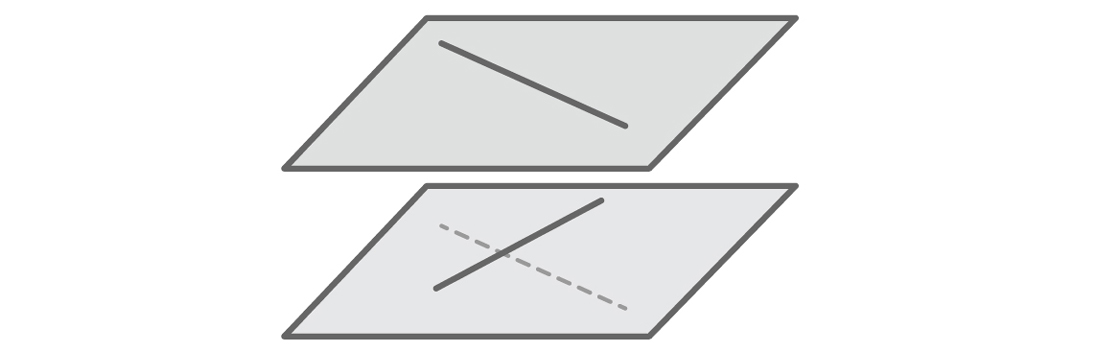
As linhas cruzadas devem estar em planos diferentes. Mas como nosso modelo define qualquer linha através da equação y = mx + b, automaticamente imaginamos que todas as linhas estão no mesmo plano. Nosso modelo fornecerá apenas fatos que sustentam nossa hipótese, porque, se duas linhas estiverem no mesmo plano, elas realmente deverão se cruzar ou ficar paralelas. Não veremos outros fatos: não há linhas de interseção em nosso modelo. Como no caso das linhas verticais, o modelo descartou o que não poderíamos imaginar.
Este é um exemplo simples usando um modelo estúpido com vários problemas, incluindo perguntas complicadas, como o procedimento para escolher números aleatórios em conjuntos infinitos. Os matemáticos profissionais que estudam as fileiras das curvas elípticas nunca teriam cometido erros tão simplificados e óbvios.
Esses matemáticos sabem quais precauções devem ser tomadas ao trabalhar com modelos. Eles sabem que, independentemente de quão útil e interessante seja o modelo ou de quão convincentes serão os fatos coletados, as curvas elípticas podem revelar propriedades que eles não imaginavam. E se isso não puder ser imaginado, seu modelo não levará isso em consideração e, portanto, os fatos não serão refletidos.
Mas se o novo modelo está certo ou não, forçou os matemáticos a pensar produtivamente sobre as curvas elípticas. Se ele realmente reflete a verdade, as idéias do mundo das matrizes podem explicar o comportamento das curvas. Caso contrário, entender por que as curvas elípticas não podem ser modeladas dessa maneira pode levar a uma melhor compreensão do problema. Os fatos que coletamos podem nos aproximar da prova, de um jeito ou de outro.