1. Introdução
Este artigo é uma continuação de uma
série de artigos que descrevem os algoritmos subjacentes.
O Synet é uma estrutura para o lançamento de redes neurais pré-treinadas na CPU.
Se você observar a distribuição do tempo do processador gasto na propagação direta do sinal em redes neurais, acontece que geralmente mais de 90% de todo o tempo é gasto em camadas convolucionais. Portanto, se queremos obter um algoritmo rápido para uma rede neural, precisamos, antes de tudo, de um algoritmo rápido para uma camada convolucional. Neste artigo, quero descrever métodos para otimizar a propagação direta de sinal em uma camada convolucional. E eu quero começar com os métodos mais usados com base na multiplicação de matrizes. Tentarei manter a apresentação da forma mais acessível, para que o artigo seja interessante não apenas para especialistas (eles já sabem tudo sobre ele), mas também para um círculo mais amplo de leitores. Não pretendo ser uma revisão completa; portanto, quaisquer comentários e adições são bem-vindos.
Opções da camada de convolução
Eu gostaria de começar a descrição com uma descrição dos parâmetros que estão na camada convolucional. Os especialistas podem pular com segurança esta seção.
Tamanhos de imagem de entrada e saída
Em primeiro lugar, uma camada convolucional é caracterizada por uma imagem de entrada e uma saída, caracterizadas pelos seguintes parâmetros:

- srcC / dstC - o número de canais na imagem de entrada e saída. Notação alternativa: C / D.
- srcH / dstH - altura da imagem de entrada e saída. Designação alternativa: H.
- srcW / dstW - largura da imagem de entrada e saída. Designação alternativa: W.
- lote - o número de imagens de entrada (saída) - a camada pode processar um lote inteiro de imagens por vez. Designação alternativa: N.
Tamanhos principais de convolução
A operação de convolução é inerentemente uma soma ponderada de uma determinada vizinhança de um determinado ponto da imagem. O tamanho do kernel de convolução - caracteriza o tamanho desse bairro e é descrito por dois parâmetros:

- kernelY é a altura do kernel de convolução. Designação alternativa: Y.
- kernelX é a largura do kernel de convolução. Designação alternativa: X.
As convoluções mais comuns com um tamanho de núcleo de
1x1 e
3x3 . Os tamanhos
5x5 e
7x7 são muito menos comuns. Às vezes, também são encontrados tamanhos grandes de convolução, bem como convoluções com um núcleo diferente de quadrado, mas isso é mais exótico.
Etapa de convolução
Outro parâmetro importante é a etapa de convolução:

- strideY é a etapa de convolução vertical.
- strideX - etapa de convolução horizontal.
Se a etapa for diferente de
1x1 , por exemplo -
2x2 , a imagem de saída será a metade (a convolução será calculada apenas na vizinhança de pontos pares).
Convolução de alongamento
O kernel de convolução pode ser expandido (aumente o tamanho efetivo da janela, mantendo o número de operações) usando os seguintes parâmetros:
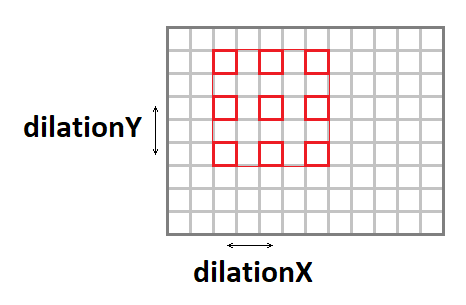
- dilataçãoY - alongamento vertical da convolução.
- dilataçãoX - alongamento horizontal da convolução.
Vale a pena notar que casos com alongamentos diferentes de
1x1 são uma ocorrência bastante rara (nunca encontrei isso na minha carreira).
Padding Input Image
Se você aplicar uma convolução com uma janela diferente de uma única para a imagem, a imagem de saída será menor pela quantidade de
kernel - 1 . O pacote, por assim dizer, "come" as bordas. Para preservar o tamanho da imagem, a imagem de entrada geralmente é preenchida nas bordas com zeros. Mais quatro parâmetros são responsáveis por isso:

- padY / padX - preenchimento vertical e horizontal frontal.
- padH / padW - preenchimento traseiro vertical e horizontal.
Grupos de canais
Normalmente, cada canal de saída é a soma das convoluções em todos os canais de entrada. No entanto, esse nem sempre é o caso. É possível dividir os canais de entrada e saída em grupos, a soma é realizada apenas dentro dos grupos:

- grupo - o número de grupos.
Na prática, as situações com
grupo = 1 e
grupo = srcC = dstC , a chamada
convolução em profundidade, são mais frequentemente encontradas.
Função de deslocamento e ativação
Embora formalmente a função de deslocamento e ativação não esteja incluída na convolução, mas muitas vezes essas duas operações seguem a camada convolucional, por que geralmente também estão incluídas nela. Tendo em vista a variedade de possíveis funções de ativação e seus parâmetros, não os descreverei aqui em detalhes.
Implementação básica do algoritmo
Para começar, gostaria de fornecer uma implementação básica do algoritmo:
float relu(float value) { return value > 0 ? return value : 0; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int b = 0; b < batch; ++b) { for (int g = 0; g < group; ++g) { for (int dc = 0; dc < dstC / group; ++dc) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { float sum = 0; for (int sc = 0; sc < srcC / group; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) sum += src[((b * srcC + sc)*srcH + sy)*srcW + sx] * weight[((dc * srcC / group + sc)*kernelY + ky)*kernelX + kx]; } } } dst[((b * dstC + dc)*dstH + dy)*dstW + dx] = relu(sum + bias[dc]); } } } } } }
Nesta implementação, assumi que a imagem de entrada e saída está no formato
NCHW :
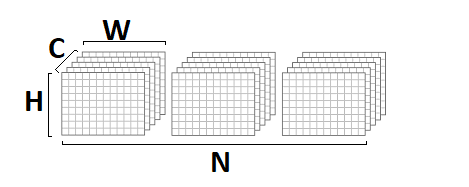
os pesos de convolução são armazenados no formato
DCYX e nossa função de ativação é
ReLU . No caso geral, isso não é verdade, mas para a implementação básica, essas suposições são bastante apropriadas - você precisa começar de alguma coisa.
Temos 8 ciclos aninhados e o número total de operações:
batch * kernelY * kernelX * srcC * dstH * dstW * dstC / group * 2,
enquanto a quantidade de dados na entrada:
batch * srcC * srcH * srcW,
e imagem de saída:
batch * dstC * dstH * dstW,
e o número de pesos:
kernelY * kernelX * srcC * dstC / group.
Se o
grupo << srcC (o número de grupos for muito menor que o número de canais), bem como com parâmetros suficientemente grandes
srcC ,
srcH ,
srcW e
dstC , obteremos um problema computacional clássico quando o número de cálculos exceder significativamente a quantidade de dados de entrada e saída. I.e. A operação de convolução com implementação adequada deve basear-se nos recursos de computação do processador e não na largura de banda da memória. Resta apenas encontrar essa implementação.
Redução do problema para multiplicação de matrizes
A operação principal na convolução é obter uma soma ponderada e os pesos são os mesmos para todos os pontos da imagem de saída. Se você reorganizar a imagem de entrada da seguinte maneira:
void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int sc = 0; sc < srcC; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[((b * srcC + sc)*srcH + sy)*srcW + sx]; else *buf++ = 0; } } } } } }
Depois
mudaremos do formato
srcC - srcH - srcW para o formato
srcC - kernelY - kernelX - dstH - dstW . A figura abaixo mostra como a imagem é convertida com o preenchimento
1 e
3x3 :
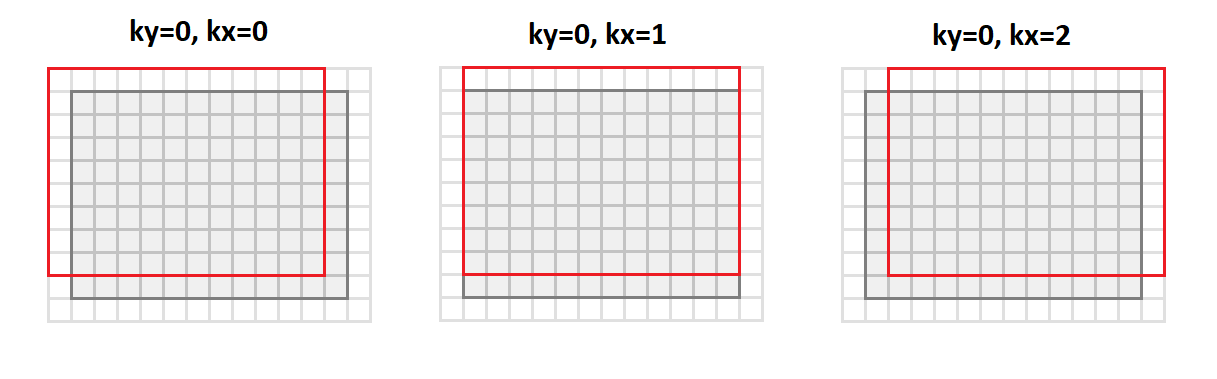
Nesse caso, todos os pontos da vizinhança da imagem necessários para a operação de convolução estão alinhados ao longo das colunas da matriz resultante (daí o seu nome -
importe para colunas).
A nova representação da imagem de entrada é interessante, pois agora a operação de convolução em nós é reduzida à multiplicação da matriz:
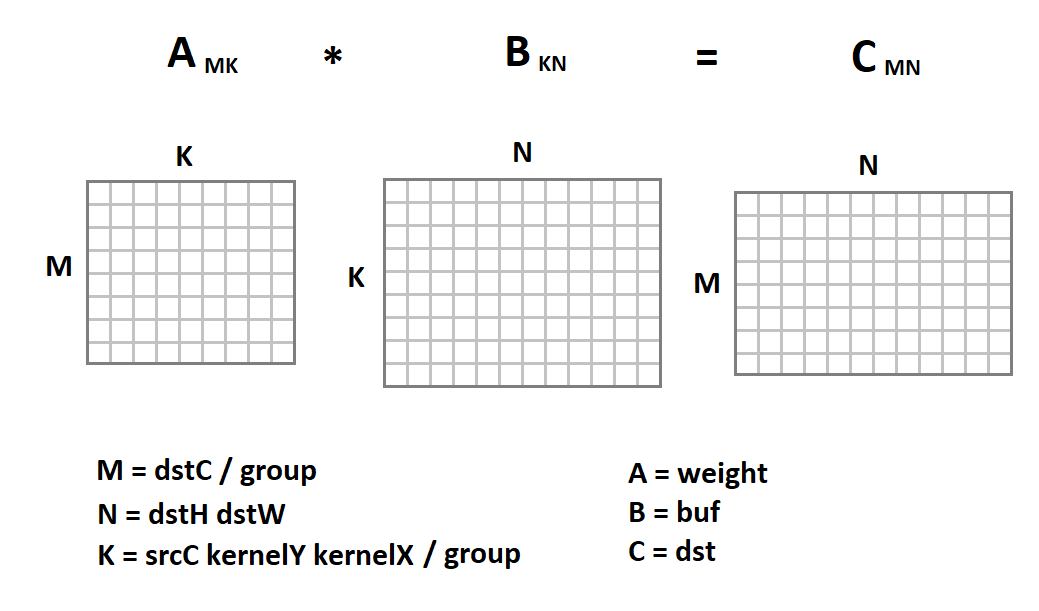
Agora o código de convolução ficará assim:
void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) { for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstC / group; int N = dstH * dstW; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, weight + M * K * g, K, 0, buf + N * K * g, N, dst + M * N * g, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } }
Aqui a implementação trivial da multiplicação de matrizes é dada apenas como exemplo. Podemos substituí-lo por qualquer outra implementação. Felizmente, a multiplicação de matrizes é uma operação estabelecida há muito tempo que já foi implementada em muitas bibliotecas com eficiência muito alta (até 90% do desempenho da CPU teoricamente possível). No tópico de como essa eficiência é alcançada, tenho até um
artigo separado .
Usando multiplicação de matrizes para o formato NHWC
Juntamente com o formato
NCHW , o
NHWC é frequentemente usado no aprendizado de máquina:

Como exemplo, observe que o
NHWC é o formato nativo do
Tensorflow .
Vale ressaltar que, para esse formato, a operação de convolução também pode levar à multiplicação da matriz. Para fazer isso, do formato
srcH - srcW - srcC, traduzimos a imagem original para o formato
dstH - dstW - kernelY - kernelX - srcC usando a função
im2row :
void im2row(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int g = 0; g < group; ++g) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; for (int sc = 0; sc < srcC; ++sc) { if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[(sy * srcW + sx)*srcC + sc]; else *buf++ = 0; } } } } } src += srcC / group; } }
Além disso, todos os pontos da vizinhança da imagem necessários para a operação de convolução estão alinhados ao longo das linhas da matriz resultante (daí o seu nome -
importe para as linhas ). Também devemos alterar o formato de armazenamento das escalas de convolução do formato
DCYX para o formato
YXCD . Agora podemos aplicar a multiplicação de matrizes:

Diferentemente do formato
NCHW , multiplicamos a matriz da imagem pela matriz de peso e não vice-versa. A seguir está um código de função de convolução:
void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstH * dstW; int N = dstC / group; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2row(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, group, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, buf + M * K * g, K * group, 0, weight + N * g, dstC, dst + N * g, dstC)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } }
Vantagens e desvantagens do método
Desde o início, gostaria de listar as vantagens dessa abordagem:
- Este método tem uma implementação muito simples. Não é à toa que é usado em quase todas as bibliotecas que conheço.
- A eficácia do método para muitos casos é muito alta: a partir de unidades de porcentagem na versão básica, atingimos mais de 80% do máximo teórico.
- A abordagem é universal - temos um código para todos os parâmetros possíveis da camada convolucional (e há muitos deles!). Portanto, esse método geralmente funciona nos casos em que abordagens mais eficazes (e, portanto, mais especializadas) têm limitações.
- A abordagem funciona para os principais formatos de tensores de imagem - NCHW e NHWC .
Agora, sobre as desvantagens:
- Infelizmente, a multiplicação de matrizes padrão é efetiva desde que os valores dos parâmetros M, N, K sejam grandes o suficiente e, além disso, tenham aproximadamente a mesma ordem de magnitude (a eficiência é baseada no fato de que o número necessário de cálculos é ~ O (N ^ 3) e a taxa de transferência necessária capacidade de memória ~ O (N ^ 2) ). Portanto, se algum dos parâmetros M, N, K for pequeno, a eficiência do método cai acentuadamente.
- O método requer a conversão de dados de entrada. E isso está longe de ser uma operação gratuita. Ela só pode ser negligenciada se K for grande o suficiente. E se levarmos em conta que dentro da multiplicação da matriz padrão ainda há uma transformação interna dos dados de entrada, a situação se torna ainda mais triste.
- Com base no fato de que K = srcC * kernelY * kernelX / group , a eficiência do método é especialmente baixa para as camadas convolucionais de entrada. E para a convolução profunda, o método da matriz geralmente perde para a implementação trivial.
- O método requer processamento adicional da saída para a operação de mudança e o cálculo da função de ativação.
- Existem métodos matemáticos mais eficientes para calcular a convolução, que exigem menos operações.
Conclusões
O método de cálculo da convolução com base na multiplicação de matrizes é simples de implementar e possui alta eficiência. Infelizmente, não é universal. Em vários casos especiais, existem abordagens mais rápidas, cuja descrição gostaria de adiar para os próximos artigos desta
série . À espera de feedback e comentários dos leitores. Espero que você esteja interessado!
PS Esta e outras abordagens são implementadas por mim no
Convolution Framework como parte da biblioteca
Simd .
Essa estrutura é subjacente ao
Synet , uma estrutura para executar redes neurais pré-treinadas na CPU.