Prefácio
Não faz muito tempo, tive que trabalhar com a simplificação da cadeia poligonal (um
processo que permite reduzir o número de pontos de polilinha ). Em geral, esse tipo de tarefa é muito comum ao processar gráficos vetoriais e ao criar mapas. Como exemplo, podemos pegar uma cadeia cujos vários pontos caem no mesmo pixel - é óbvio que todos esses pontos podem ser simplificados em um. Há algum tempo, eu praticamente não sabia nada sobre isso com a palavra “completamente” e, portanto, tive que preencher rapidamente o conhecimento necessário sobre esse tópico. Mas qual foi minha surpresa quando não encontrei manuais completos suficientes na Internet na Internet ... Eu tive que pesquisar trechos de informações de fontes completamente diferentes e, após a análise, transformar tudo em um quadro geral. A ocupação não é das mais agradáveis, para ser sincera. Portanto, gostaria de escrever uma série de artigos sobre algoritmos de simplificação de cadeia poligonal. Eu apenas decidi começar com o algoritmo Douglas-Pecker mais popular.
Descrição do produto
O algoritmo define a polilinha inicial e a distância máxima (ε), que pode estar entre as polilinhas originais e simplificadas (ou seja, a distância máxima entre os pontos do original e a seção mais próxima da polilinha resultante). O algoritmo divide recursivamente a polilinha. A entrada para o algoritmo são as coordenadas de todos os pontos entre o primeiro e o último, incluindo-os, bem como o valor de ε. O primeiro e o último ponto são mantidos inalterados. Depois disso, o algoritmo encontra o ponto mais distante do segmento que consiste no primeiro e no último (
o algoritmo de pesquisa é a distância do ponto ao segmento ). Se o ponto estiver localizado a uma distância menor que ε, todos os pontos que ainda não foram marcados para preservação podem ser ejetados do conjunto, e a linha reta resultante suaviza a curva com uma precisão de pelo menos ε. Se essa distância for maior que ε, o algoritmo se chamará recursivamente no conjunto do ponto inicial ao dado e do dado aos pontos finais.
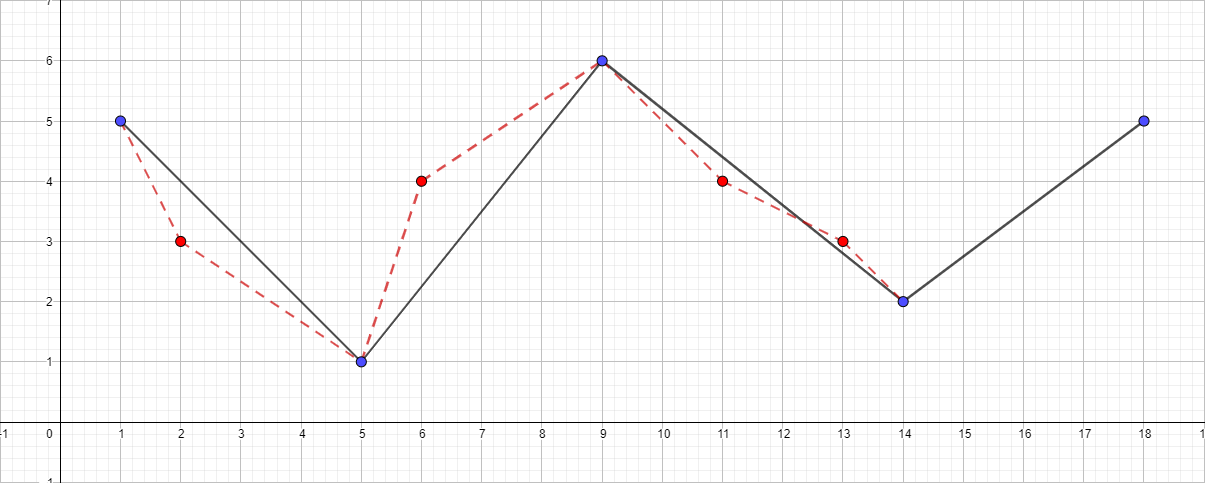
Vale ressaltar que o algoritmo Douglas-Pecker não preserva a topologia no decorrer de seu trabalho. Isso significa que, como resultado, podemos obter uma linha com auto-interseções. Como exemplo ilustrativo, faça uma polilinha com o seguinte conjunto de pontos: [{1; 5}, {2; 3}, {5; 1}, {6; 4}, {9; 6}, {11; 4}, {13; 3}, {14; 2}, {18; 5}] e observe o processo de simplificação para diferentes valores de ε:
A polilinha original do conjunto de pontos apresentado:

Polilinha com ε igual a 0,5:
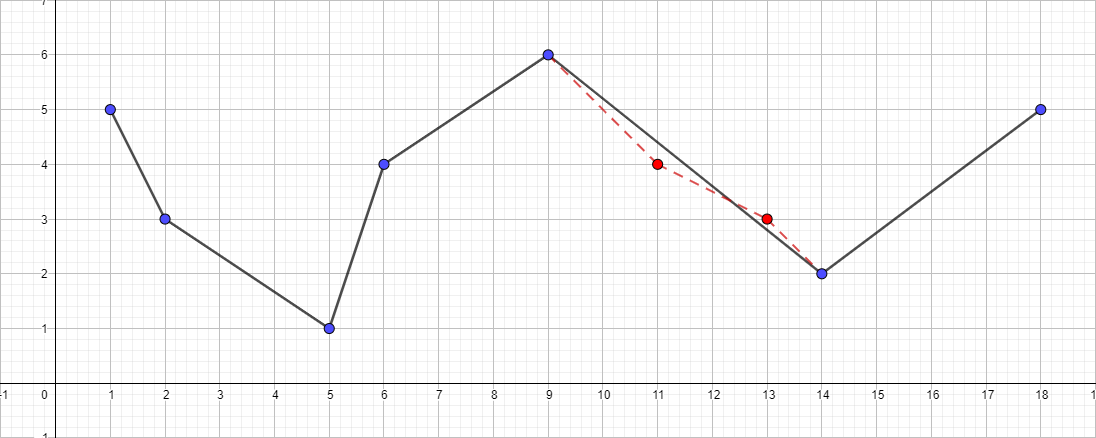
Uma polilinha com ε igual a 1:

Polilinha com ε igual a 1,5:
Você pode continuar aumentando a distância máxima e visualizando o algoritmo, mas acho que o ponto principal depois desses exemplos ficou claro.
Implementação
O C ++ foi escolhido como a linguagem de programação para a implementação do algoritmo, o código fonte completo do algoritmo que você pode ver
aqui . E agora diretamente para a própria implementação:
#define X_COORDINATE 0 #define Y_COORDINATE 1 template<typename T> using point_t = std::pair<T, T>; template<typename T> using line_segment_t = std::pair<point_t<T>, point_t<T>>; template<typename T> using points_t = std::vector<point_t<T>>; template<typename CoordinateType> double get_distance_between_point_and_line_segment(const line_segment_t<CoordinateType>& line_segment, const point_t<CoordinateType>& point) noexcept { const CoordinateType x = std::get<X_COORDINATE>(point); const CoordinateType y = std::get<Y_COORDINATE>(point); const CoordinateType x1 = std::get<X_COORDINATE>(line_segment.first); const CoordinateType y1 = std::get<Y_COORDINATE>(line_segment.first); const CoordinateType x2 = std::get<X_COORDINATE>(line_segment.second); const CoordinateType y2 = std::get<Y_COORDINATE>(line_segment.second); const double double_area = abs((y2-y1)*x - (x2-x1)*y + x2*y1 - y2*x1); const double line_segment_length = sqrt(pow((x2-x1), 2) + pow((y2-y1), 2)); if (line_segment_length != 0.0) return double_area / line_segment_length; else return 0.0; } template<typename CoordinateType> void simplify_points(const points_t<CoordinateType>& src_points, points_t<CoordinateType>& dest_points, double tolerance, std::size_t begin, std::size_t end) { if (begin + 1 == end) return; double max_distance = -1.0; std::size_t max_index = 0; for (std::size_t i = begin + 1; i < end; i++) { const point_t<CoordinateType>& cur_point = src_points.at(i); const point_t<CoordinateType>& start_point = src_points.at(begin); const point_t<CoordinateType>& end_point = src_points.at(end); const double distance = get_distance_between_point_and_line_segment({ start_point, end_point }, cur_point); if (distance > max_distance) { max_distance = distance; max_index = i; } } if (max_distance > tolerance) { simplify_points(src_points, dest_points, tolerance, begin, max_index); dest_points.push_back(src_points.at(max_index)); simplify_points(src_points, dest_points, tolerance, max_index, end); } } template< typename CoordinateType, typename = std::enable_if<std::is_integral<CoordinateType>::value || std::is_floating_point<CoordinateType>::value>::type> points_t<CoordinateType> duglas_peucker(const points_t<CoordinateType>& src_points, double tolerance) noexcept { if (tolerance <= 0) return src_points; points_t<CoordinateType> dest_points{}; dest_points.push_back(src_points.front()); simplify_points(src_points, dest_points, tolerance, 0, src_points.size() - 1); dest_points.push_back(src_points.back()); return dest_points; }
Bem, na verdade, o uso do próprio algoritmo:
int main() { points_t<int> source_points{ { 1, 5 }, { 2, 3 }, { 5, 1 }, { 6, 4 }, { 9, 6 }, { 11, 4 }, { 13, 3 }, { 14, 2 }, { 18, 5 } }; points_t<int> simplify_points = duglas_peucker(source_points, 1); return EXIT_SUCCESS; }
Exemplo de execução de algoritmo
Como entrada, usamos um conjunto de pontos conhecido anterior [{1; 5}, {2; 3}, {5; 1}, {6; 4}, {9; 6}, {11; 4}, {13; 3}, {14; 2}, {18; 5}] e ε igual a 1:
- Encontre o ponto mais distante do segmento {1; 5} - {18; 5}, este ponto será o ponto {5; 1}.
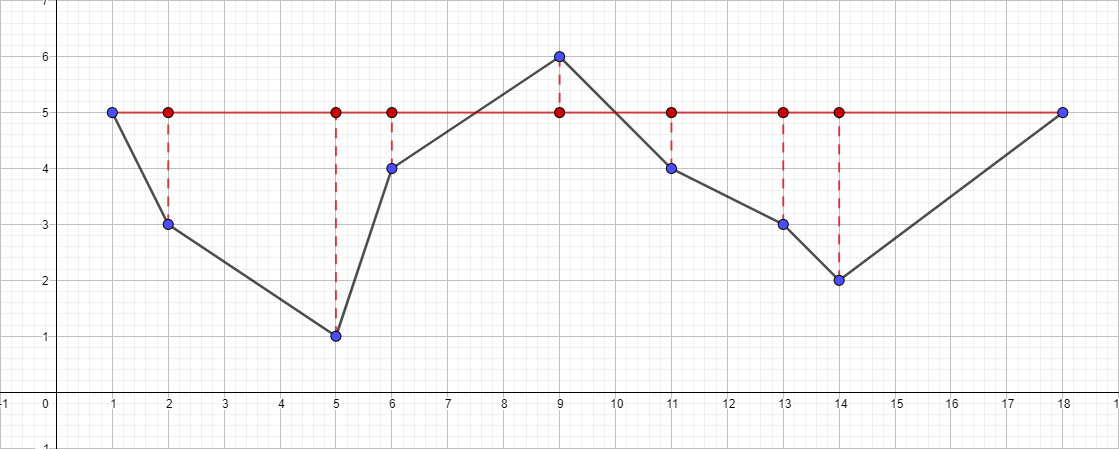
- Verifique sua distância para o segmento {1; 5} - {18; 5}. É mais do que 1, o que significa que a adicionamos à polilinha resultante.
- Execute recursivamente o algoritmo para o segmento {1; 5} - {5; 1} e encontre o ponto mais distante para esse segmento. Este ponto é {2; 3}.
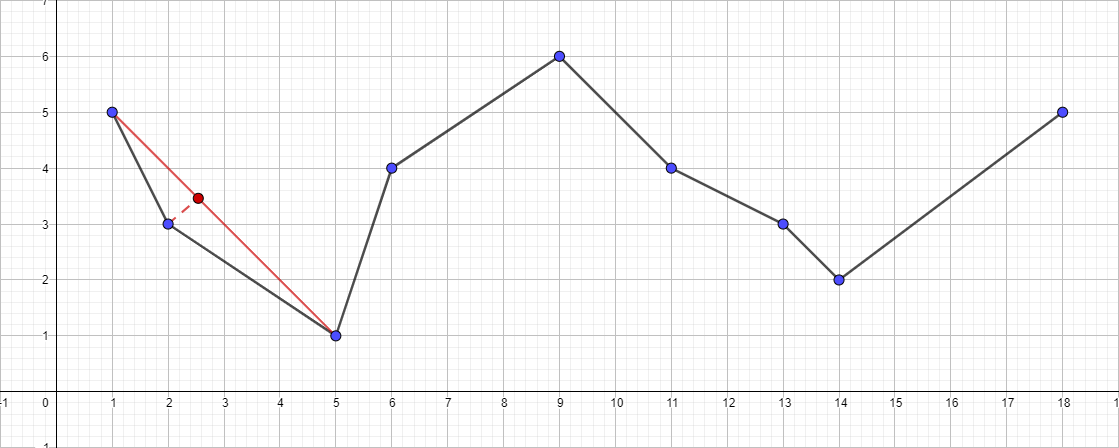
- Verifique sua distância para o segmento {1; 5} - {5; 1}. Nesse caso, é menor que 1, o que significa que podemos descartar com segurança esse ponto.
- Execute recursivamente o algoritmo para o segmento {5; 1} - {18; 5} e encontre o ponto mais distante para esse segmento ...
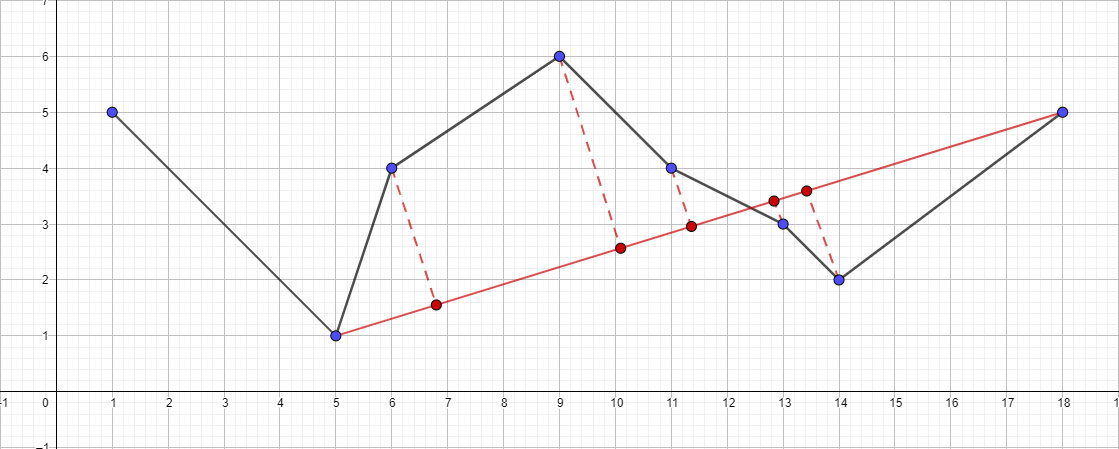
- E assim por diante, de acordo com o mesmo plano ...
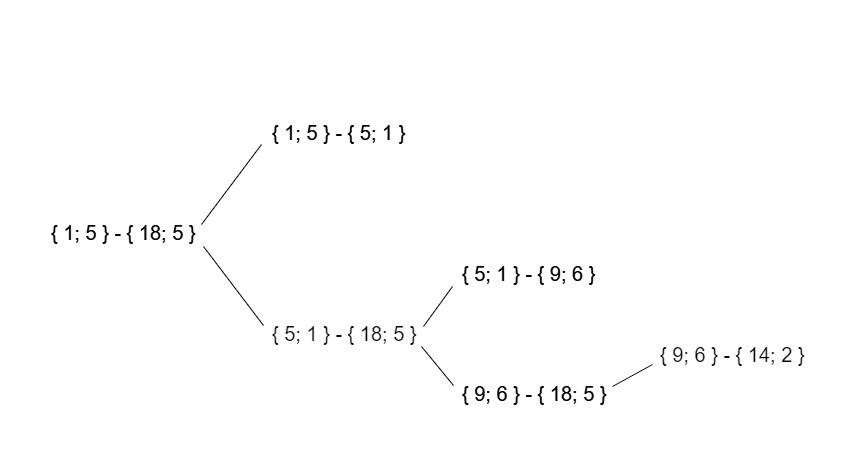
Como resultado, a árvore de chamadas recursivas para esses dados de teste terá a seguinte aparência:
Tempo de trabalho
A complexidade esperada do algoritmo, na melhor das hipóteses, é O (nlogn), é quando o número do ponto mais distante é sempre lexicograficamente central. No entanto, no pior caso, a complexidade do algoritmo é O (n ^ 2). Isso é alcançado, por exemplo, se o número do ponto mais distante for sempre adjacente ao número do ponto de limite.
Espero que meu artigo seja útil para alguém, também gostaria de chamar a atenção para o fato de que, se o artigo mostrar interesse suficiente entre os leitores, em breve estarei pronto para considerar algoritmos para simplificar a cadeia poligonal de Reumman-Witkam, Opheim e Lang. Obrigado pela atenção!