Sobre como remover uma tendência de dados experimentais

Ao analisar séries temporais estacionárias obtidas experimentalmente, como regra, durante a preparação preliminar (pré-processamento) dos dados, torna-se necessário suprimir a tendência existente neles.

Aqui será proposto um “novo” método de destaque de tendência - simples, óbvio e adequado para tipos de tendência muito complexos.

Uma tendência é geralmente entendida como um componente não harmônico de frequência ultra baixa que viola acentuadamente a estacionariedade do processo. A causa mais comum de uma tendência nos dados obtidos experimentalmente é o "desvio zero" do equipamento de gravação. A integração de dados e alguns outros tipos de processamento também podem causar uma tendência. A presença de uma tendência distorce bastante os resultados do processamento de dados subsequente (estimativa espectral etc.), portanto, a remoção da tendência é necessária. Em alguns casos, a tendência em si é uma fonte valiosa de informação (por exemplo, ao analisar tendências de longo prazo em processos econômicos ou meteorológicos).


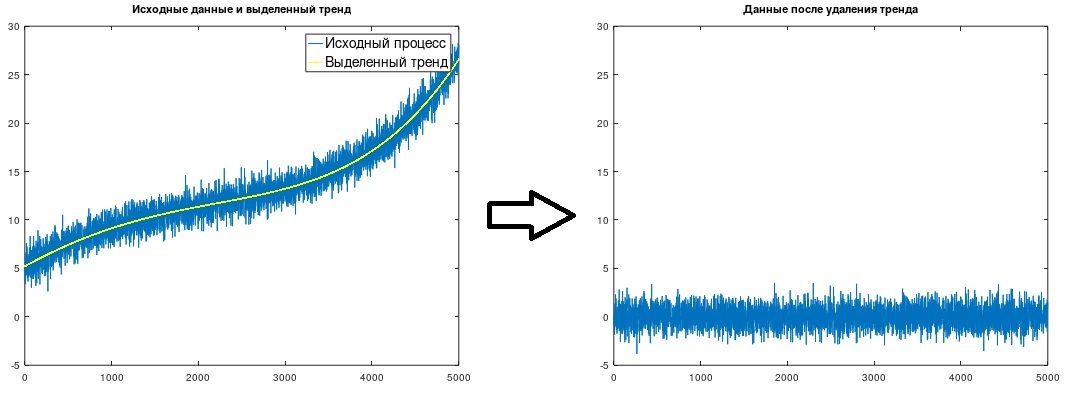Fig. 1. Isolamento e remoção de uma tendência

Tipicamente, uma tendência é modelada usando funções lineares ou de potência (2ª ou 3ª ordem), cujos coeficientes são calculados multiplicando o processo por certas sequências e aplicando fórmulas bastante complexas derivadas do método dos mínimos quadrados. (veja, por exemplo, J. Bendat, A. Pirsol, “Análise Aplicada de Dados Aleatórios”, M., Mir, 1989.) A seguir, é apresentado um método ligeiramente modificado, também baseado no método dos mínimos quadrados, que é muito fácil de entender e aprender, e não requer referência a diretórios ou cálculos simbólicos complexos independentes para obter as dependências necessárias, permitindo modelar a tendência com funções de qualquer tipo. Esse método modificado é tão simples e óbvio (depois de dominado, os scripts podem ser gravados na memória) que provavelmente foi "inventado" por diferentes pesquisadores mais de uma vez, mas ainda não encontrei nada em nenhuma das fontes.

Para destacar a tendência, é realizada uma aproximação do processo inicial x [i], consistindo em amostras N + 1, usando um pequeno número de k funções que compõem a tendência u _j [i]:


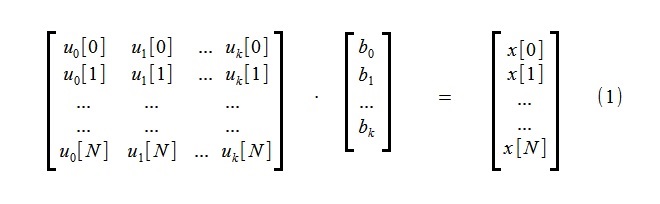
(Geralmente, as funções de potência são escolhidas como funções u _j [i],



mas para este método é absolutamente sem princípios)

O sistema de equações algébricas lineares (1) inclui k equações desconhecidas b _j e N + 1.

Tomando a notação:



escreva de forma mais compacta



A aplicação do método dos mínimos quadrados na busca de uma solução aproximada de um sistema sobredeterminado é escrita na forma de matriz da seguinte maneira:



Ao escrever um script: Naturalmente, não há necessidade de armazenar toda a matriz grande U, os elementos da matriz U ^T U e o vetor U ^T x podem ser "acumulados" passo a passo.

O sistema (4) de k equações e k incógnitas é resolvido por métodos óbvios - bem, por exemplo, escrevemos assim:



após o qual, usando o _j encontrado, podemos construir a tendência θ [i] na forma



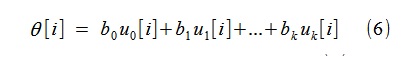
Por exemplo, um processo aleatório x [i] do formulário foi simulado



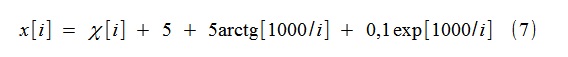
where χ [i] - ruído branco gaussiano com uma única dispersão. A tendência é modelada por funções do tipo (2) (mais precisamente, (8)), até e incluindo a 4ª ordem (k = 4).

Ao usar funções de lei de potência para modelagem de tendências, deve-se notar que a matriz U ^T U (4) é teoricamente sempre reversível devido à independência linear dessas funções; no entanto, em ordens elevadas de k (ou realizações muito longas de N, que é menos crítico), alguns de seus elementos podem ser muito ótimo em valor absoluto. Em ordens altas de k, em caso de dificuldades computacionais, recomenda-se o uso de coeficientes redutores, por exemplo, como (8):



(Δt = 1), o que foi feito no exemplo considerado. A tendência mostrada na Fig. 1 é obtida.
Depois de destacar uma tendência, naturalmente, ela deve ser subtraída dos dados de origem.

Observação. Normalmente, fontes autorizadas não recomendam trabalhar com modelos de tendência da ordem acima k = 2 (parábola quadrada). Se isso se deve à dificuldade de determinar os coeficientes de "amplitude" _{bj pelos} métodos tradicionais, ou ao esgotamento das ordens das variáveis ​​de máquina mencionadas acima ou à designação falsa de componentes informativos do processo à tendência, não está muito claro. No exemplo dado, a tendência de 4ª ordem é destacada como se fosse bastante plausível (embora não muito diferente da tendência de 3ª ordem). Para casos particularmente difíceis, as fontes recomendam o uso de um método diferente - filtragem passa-baixo (não considerada aqui).

Destacando uma tendência, como mostrado acima, o procedimento não é tão complicado, permite selecionar e analisar tendências “lentas” ou, mais frequentemente, ajuda a obter dados de alta qualidade - um processo aleatório estacionário centralizado adequado para análises posteriores.