
1. Introdução
Este artigo descreve os resultados de um experimento realizado no âmbito do projeto "Taxa de câmbio absoluta". O protocolo experimental pode ser visto clicando no link .
O projeto “ Taxa de câmbio absoluta ” está envolvido na análise de taxas de câmbio emparelhadas, na alocação de taxas de câmbio absolutas a partir delas e em suas análises. No âmbito do projeto, foi obtida uma metodologia para a conversão de taxas de pares em taxas de câmbio absolutas. Para isso, a moeda absoluta ABS é definida. Todas as moedas disponíveis são expressas em termos de ABS.
Uma descrição detalhada da tecnologia é fornecida no artigo " De pares de moedas a taxas de câmbio absolutas ".
Até o momento, vários artigos já foram publicados sobre a aplicação do método da taxa de câmbio absoluta. Eu trago os dois últimos.
O artigo “ Um estudo da conexão das moedas mundiais através da correlação de taxas absolutas ” descreve uma das aplicações da tecnologia das taxas de câmbio absolutas. É fornecido um método formal para calcular o relacionamento entre diferentes moedas.
O artigo " O método do portfólio de Markowitz, aplicado ao mercado de câmbio ", descreve a tecnologia anteriormente inacessível para otimizar o portfólio de moedas estrangeiras.
A seguir, descreve o método de conversão das taxas de câmbio do par (relativo) para absoluto. Os parâmetros numéricos da transformação e a metodologia para seu cálculo são fornecidos.
No arquivo de origem, as taxas de câmbio diárias são carregadas automaticamente diariamente e as absolutas são calculadas a partir delas.
A matriz de transformação foi obtida em 2017. Foi calculado com taxas de câmbio de pares reais, minimizando o erro de desvio das taxas de pares restauradas do absoluto. Desde então, nenhuma análise de erro foi realizada nos dados modernos.
Os resultados inesperados de verificação descritos abaixo levaram ao desenvolvimento de uma nova técnica para obter a matriz de transformação. Além disso, um erro foi detectado no processamento de cotações importadas.
Fundamentos teóricos
Para obter taxas de câmbio absolutas, você deve fazer a seguinte conversão. Para começar, os cursos emparelhados são logaritmos. Em seguida, multiplicamos pela matriz de transformação inversa. No final, retornamos da escala logarítmica usando um expoente.
Para a transição adicional para emparelhar cursos, é necessário registrar os cursos absolutos. Em seguida, multiplique pela matriz de transformação direta. Concluímos como antes usando o expoente.
A tecnologia é descrita em mais detalhes no artigo “ Dos pares de moedas às taxas absolutas de moedas individuais ” (somente este artigo de 2018 fornece uma representação transposta das matrizes de transformação em contraste com a apresentação deste artigo).
A matriz direta é facilmente determinada. As linhas correspondem a moedas e as colunas correspondem a pares de moedas. A matriz é muito esparsa e consiste em zeros, uns e menos.
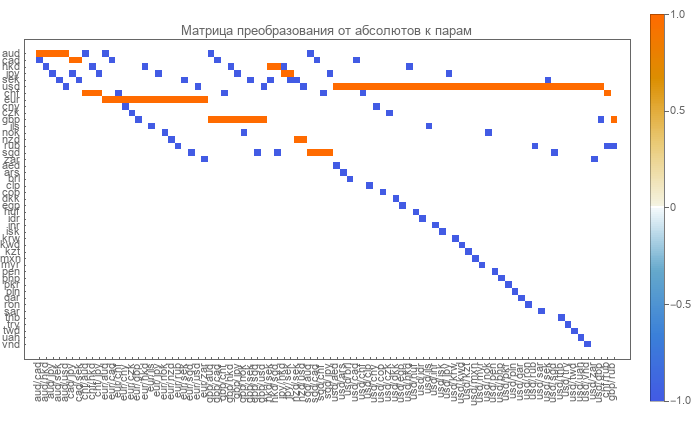
Zeros indicam a ausência desse par e moeda. A unidade corresponde à moeda no numerador do par. O menos um indica a moeda no denominador do par.
A matriz de transformação inversa de pares para taxas absolutas não está definida. Deve ser calculado. O método mais óbvio é minimizar o erro na recuperação de pares. O que foi feito para calcular essa matriz em 2017. Nós damos uma representação gráfica desta matriz.
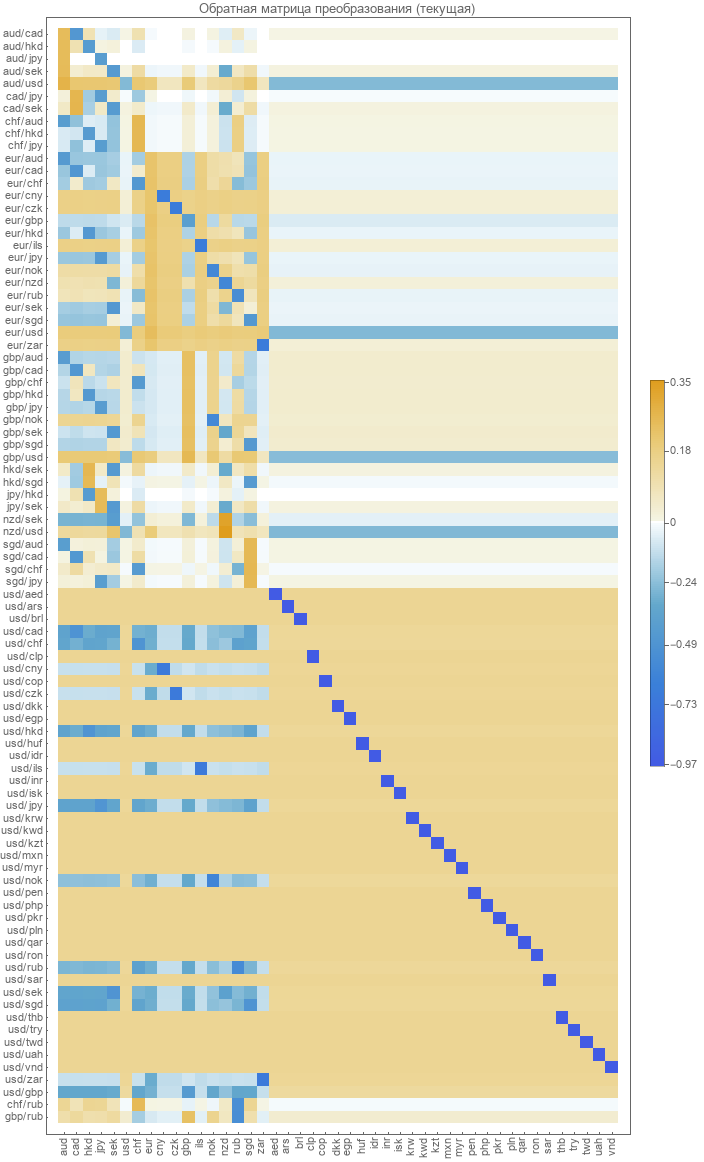
Verificando a precisão de um modelo existente
Para a matriz atual, foram obtidas taxas de câmbio de pares absolutos e restaurados. Havia diferenças acentuadas entre os cursos pareados originais e restaurados.

Em seguida, foi realizado o cálculo dos erros de recuperação para todos os pares.
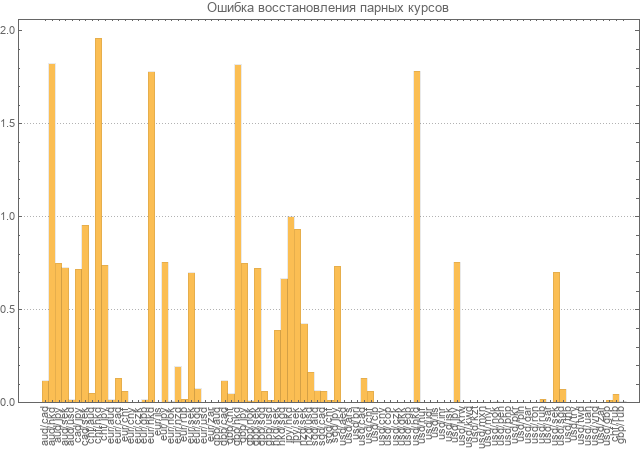
O erro foi considerado como a média dos desvios relativos obtidos no módulo. Como pode ser visto no diagrama, os erros para muitos pares são quase duas vezes maiores que os próprios valores.
Obviamente, esse nível de erro não permite que o modelo seja considerado consistente e requer recontagem.
Matriz pseudo-inversa a partir de uma linha
A primeira coisa que tentaremos é simplesmente calcular a matriz inversa para a matriz de transformação direta. Devido ao fato de a matriz não ser quadrada, teremos que usar a transformação pseudo-inversa . O resultado tem o seguinte.
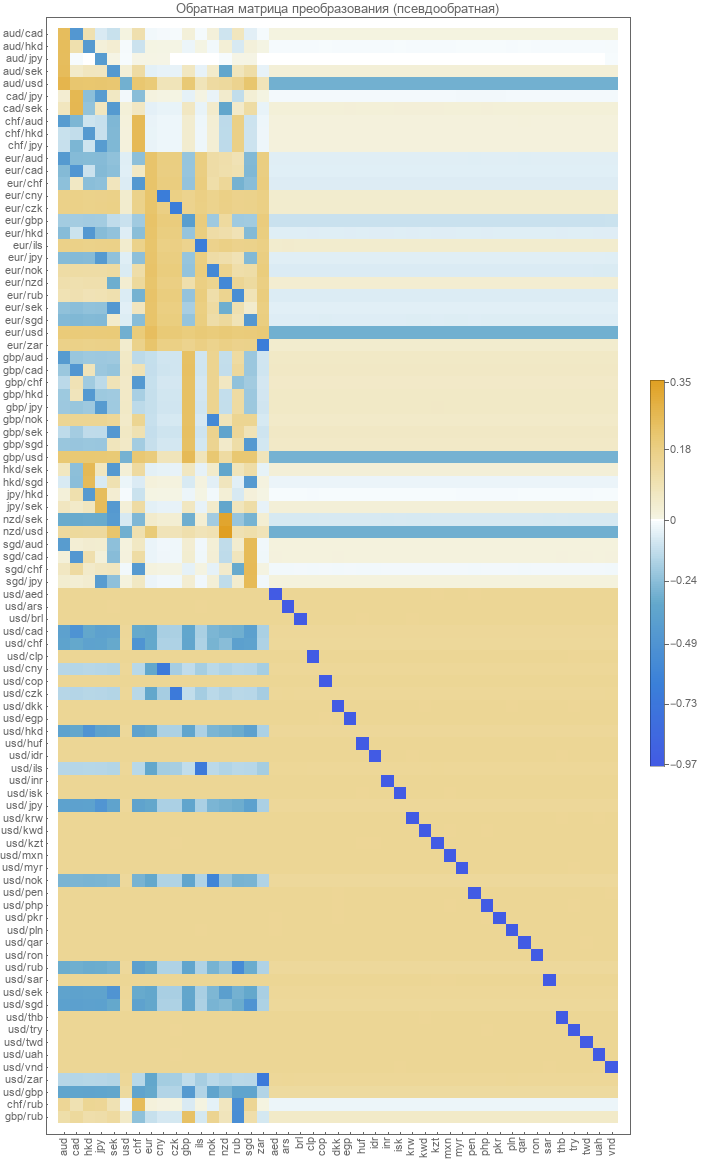
É muito semelhante ao que obtivemos anteriormente usando taxas de câmbio de pares reais para otimização.
Calculamos cursos absolutos. Em seguida, restaure a partir dos cursos de pares absolutos. O gráfico de erros é o seguinte.

Os erros também se mostraram grandes, como na avaliação acima. Este modelo também não pode ser adequado para nós.
Cálculo da matriz inversa através de componentes linearmente independentes
Se analisarmos a matriz de transformação direta em detalhes, podemos descobrir que ela possui uma forma degenerada (a classificação da matriz é menor que o número de linhas da moeda). Em outras palavras, existem linhas linearmente dependentes na matriz direta. E, portanto, não podemos obter uma matriz inversa aceitável.
Para sair dessa situação, a seguinte solução foi proposta. Na transição de cursos absolutos para emparelhados, você deve primeiro mudar para componentes linearmente independentes. E só então passar para os pares. As matrizes de transição de cursos absolutos para componentes e de componentes para cursos pareados não serão degeneradas e matrizes inversas poderão ser obtidas.
Para procurar componentes linearmente independentes, é necessário anexar uma matriz unitária de cursos em pares à matriz de transformação direta. Assim, obtemos duas matrizes da transição de cursos absolutos para pareados e a matriz anexa da transição de pareado para pareado.

Agora, realizaremos transformações padrão na forma escalonada da parte superior dessa matriz combinada (de fato, as ferramentas padrão do pacote matemático Wolfram Mathematica levam ainda mais à forma diagonal ). Como resultado, foi possível obter a seguinte matriz transformada.

Agora, nas colunas desta matriz, temos componentes linearmente independentes. Além disso, podemos mudar para eles tanto de cursos absolutos (a parte superior da matriz) quanto de cursos emparelhados (a parte inferior da matriz transformada combinada).
Selecionamos essas matrizes de transição para componentes linearmente independentes. Aqui está a matriz de transição para componentes de cursos absolutos.
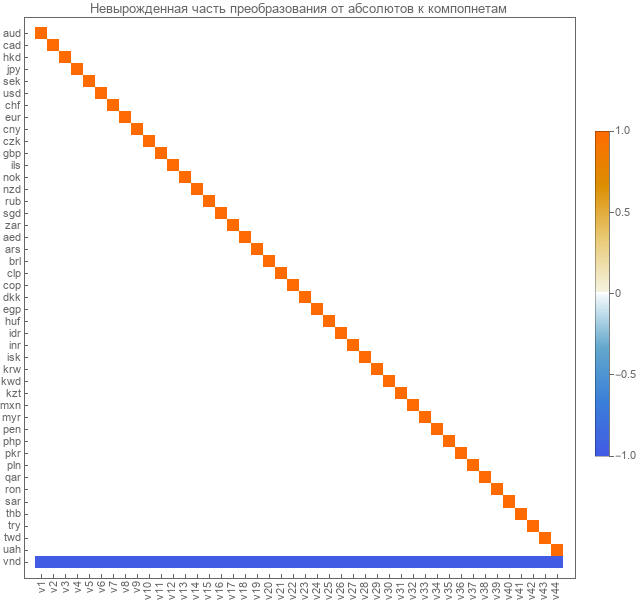
Aqui está a matriz de transição de cursos em pares para componentes linearmente independentes.

A transição de absolutos para componentes ocorre através da matriz calculada acima. A transformação inversa de componentes em absolutos é feita através da matriz inversa. Devido ao fato de que não será degenerado, uma boa matriz inversa pode ser obtida. Vamos receber como pseudo-inverso. Aqui está a visão dela.

Agora você pode obter a matriz de transformação inversa completa de pares para absolutos. Para fazer isso, multiplicamos a matriz de transformação de pares em componentes pela matriz de transformação inversa de componentes em absolutos. Ela é assim.

Embora já vimos um semelhante acima, mas ainda a matriz é diferente. Examinamos os resultados que ele fornece. Vamos calcular cursos absolutos e, a partir deles, já iremos restaurar emparelhados. O erro de recuperação foi o seguinte.

Em todos os pares, exceto dois, quase zero de erros. Descobrimos o que há de errado com esses pares.
Acontece que em dois pares de moedas os dados incorretos são aceitos. Para jpy / hkd e jpy / sek, os dados vão em lotes de 10000 e 100 partes. É necessário corrigir e verificar novamente.
Depois de corrigir os cursos de pares de entrada (eliminando lotes) e recalcular os cursos de pares absolutos e restaurados, examinamos o erro de recuperação.

Ocorreu um erro dentro de 0,3%. Um nível bastante aceitável de erro.
Aqui está um exemplo de um gráfico de curso absoluto.
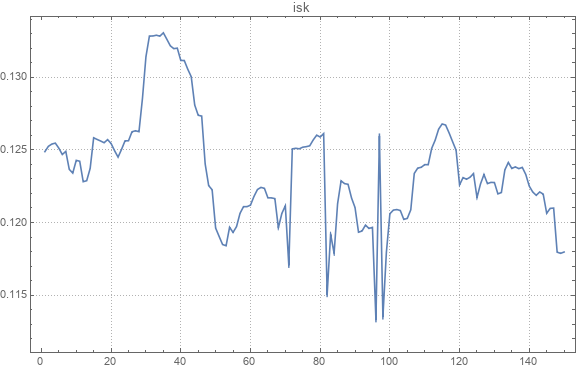
Aqui está um exemplo das taxas de câmbio de pares originais e restauradas.

Como recalculamos a nova matriz da transformação inversa, apresentamos novamente os dados das taxas absolutas mais recentes de todas as moedas participantes.
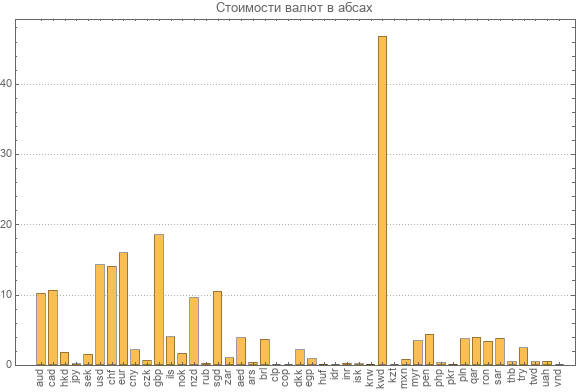
Você pode ver a moeda mais cara. Este é um dinar do Kuwait que vale quase 47 abs. O menor valor absoluto do dong vietnamita é 0,003 abs.
Conclusões
Como resultado dos estudos, verificou-se que o método existente para calcular taxas absolutas gera um erro significativo. Além disso, um erro foi detectado nos dados de origem.
Conseguimos obter a matriz de transformação inversa de pares para absolutos apenas usando o método de transformação para um número menor de componentes linearmente independentes com uma matriz de transformação não degenerada.
O método de obtenção da matriz de transformação inversa não utilizou dados de taxa de pares. E, portanto, independente deles.
A verificação da conversão em cursos reais mostrou um baixo nível de erro. A partir do qual se concluiu que a matriz encontrada da transformação inversa é aplicável das taxas de câmbio pareadas às absolutas.
O método não pretende ser concluído e verificado matematicamente, mas como uma solução aceitável, será utilizado para estudos adicionais de suas taxas de câmbio absolutas.