Hash versátil e perfeito

Começamos a semana com material útil dedicado ao lançamento do curso "Algoritmos para desenvolvedores" . Boa leitura.



1. Visão geral

Hashing é uma ótima ferramenta prática, com uma teoria interessante e sutil. Além de usar dados como uma estrutura de vocabulário, o hash também é encontrado em muitas áreas diferentes, incluindo criptografia e teoria da complexidade. Nesta palestra, descrevemos dois conceitos importantes: hash universal (também conhecido como família universal de funções de hash) e hash ideal.

O material destacado nesta palestra inclui:

• A configuração formal e a idéia geral de hash.
• Hash universal.
• Hash perfeito.

2. Introdução

Vamos considerar o principal problema com o dicionário que discutimos anteriormente e duas versões: estática e dinâmica:

• Estático : considerando muitos elementos S, queremos armazená-lo de forma que possamos executar rapidamente uma pesquisa.
• Por exemplo, um dicionário fixo.
• Dinâmico : aqui temos uma sequência de solicitações de inserção, pesquisa e possivelmente remoção. Queremos fazer tudo isso de forma eficaz.

Para o primeiro problema, poderíamos usar uma matriz classificada e uma pesquisa binária. Para o segundo, poderíamos usar uma árvore de pesquisa equilibrada. No entanto, o hash fornece uma abordagem alternativa, que geralmente é a maneira mais rápida e conveniente de resolver esses problemas. Por exemplo, suponha que você esteja escrevendo um programa para pesquisa de IA e deseje armazenar situações que você já resolveu (posições no quadro ou elementos do espaço de estados) para não repetir os mesmos cálculos ao encontrá-los novamente. O hash fornece uma maneira fácil de armazenar essas informações. Existem também muitas aplicações em criptografia, redes, teoria da complexidade.

3. Noções básicas de hash

A configuração formal para o hash é a seguinte.

• As chaves pertencem a um conjunto grande de U. (Por exemplo, imagine que U seja uma coleção de todas as cadeias com um comprimento máximo de 80 caracteres ascii.)
• Existem algumas chaves S em U que realmente precisamos (as chaves podem ser estáticas ou dinâmicas). Seja N = | S |. Imagine que N é muito menor que o tamanho de U. Por exemplo, S é o conjunto de nomes de alunos em uma classe que é muito menor que 128 ^ 80.
• Realizaremos inserções e pesquisas usando uma matriz A de algum tamanho M e uma função de hash h: U → {0, ..., M - 1}. Dado o elemento x, a idéia do hash é que queremos armazená-lo em A [h (x)]. Observe que se U fosse pequeno (por exemplo, cadeias de caracteres de 2 caracteres), você poderia salvar x em A [x], como na classificação de blocos. O problema é que U é grande, então precisamos de uma função de hash.
• Precisamos de um método para resolver colisões. Uma colisão é quando h (x) = h (y) para duas chaves diferentes x e y. Nesta palestra, lidaremos com colisões definindo cada elemento de A como uma lista vinculada. Existem vários outros métodos, mas para os problemas nos quais focaremos aqui, este é o mais adequado. Este método é chamado de método de encadeamento. Para inserir um item, basta colocá-lo no topo da lista. Se h é uma boa função de hash, esperamos que as listas sejam pequenas.

Uma das grandes vantagens do hash é que todas as operações do dicionário são incrivelmente fáceis de implementar. Para procurar a chave x, basta calcular o índice i = h (x) e, em seguida, percorrer a lista em A [i] até encontrá-la (ou sair da lista). Para inserir, basta colocar um novo item no topo de sua lista. Para excluir, basta executar a operação de exclusão na lista vinculada. Agora, passamos à pergunta: o que precisamos para obter um bom desempenho?

Propriedades desejáveis. Principais propriedades desejáveis ​​para um bom esquema de hash:

1. As chaves estão bem dispersas para que não tenhamos muitas colisões, pois elas afetam o tempo de pesquisa e exclusão.
2. M = O (N): em particular, gostaríamos que nosso circuito atingisse a propriedade (1) sem a necessidade de o tamanho da tabela M ser muito maior que o número de elementos N.
3. A função h deve ser calculada rapidamente. Em nossa análise atual, consideraremos o tempo para calcular h (x) como uma constante. No entanto, vale lembrar que não deve ser muito complicado, pois afeta o tempo de execução geral.

Diante disso, o tempo de pesquisa para o elemento x é O (o tamanho da lista é A [h (x)]). O mesmo vale para exclusões. As inserções levam tempo O (1), independentemente do tamanho das listas. Então, queremos analisar o tamanho dessas listas.

Intuição básica: uma maneira de distribuir elementos lindamente é distribuí-los aleatoriamente. Infelizmente, não podemos apenas usar o gerador de números aleatórios para decidir para onde direcionar o próximo elemento, porque nunca mais o encontraremos. Então, queremos que ele seja algo "pseudo-aleatório" em algum sentido formal.

Agora apresentaremos más notícias e outras boas.

Instrução 1 (más notícias) Para qualquer função de hash h se | U | ≥ (N −1) M +1, há um conjunto S de N elementos que todos os hash em um só lugar.

Prova: pelo princípio de Dirichlet. Em particular, para considerar contrapontos, se cada local não tivesse mais do que N - 1 elementos de U que o misturassem, então U poderia ter um tamanho não superior a M (N - 1).

É em parte por isso que o hash parece tão misterioso - como se pode argumentar que o hash é bom se, para qualquer função de hash, você puder pensar em maneiras de evitá-lo? Uma resposta é que existem muitas funções simples de hash que funcionam bem na prática para conjuntos típicos S. Mas e se quisermos uma boa garantia do pior caso?

Aqui está a idéia principal: vamos usar a randomização em nosso construto h, semelhante ao quicksort randomizado. (Escusado será dizer que h será uma função determinística). Mostraremos que, para qualquer sequência de operações de inserção e pesquisa (não precisamos assumir que o conjunto de elementos S inseridos é aleatório), se escolhermos h dessa maneira probabilística, o desempenho de h nessa sequência será bom em antecipação. Portanto, essa é a mesma garantia que em quicksort ou armadilhas aleatórias. Em particular, essa é a idéia do hash universal.

Depois de desenvolvermos essa idéia, a usaremos para um aplicativo particularmente agradável chamado "hash perfeito".

4. Hash Universal

Definição 1. Um algoritmo aleatório H para construir funções de hash h: U → {1, ..., M}
universal se para todos x! = y em U tivermos



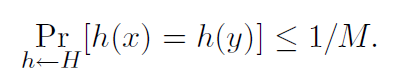
Também podemos dizer que o conjunto H de funções hash é uma família universal de funções hash se o procedimento “selecionar aleatoriamente h ∈ H” for universal. (Aqui, identificamos o conjunto de funções com uma distribuição uniforme sobre o conjunto.)

Teorema 2. Se H é universal, então para qualquer conjunto S ⊆ U de tamanho N, para qualquer x ∈ U (por exemplo, o que poderíamos procurar), se construirmos h aleatoriamente de acordo com H, o número esperado de colisões entre x e outros elementos em S não mais que N / M.

Prova: cada y ∈ S (y! = X) tem no máximo 1 / M de chance de uma colisão com x pela definição de “universal”. Então

• Deixe Cxy = 1 se x e y colidirem, e 0 caso contrário.
• Deixe Cx denotar o número total de colisões para x. Então, Cx = Py∈S, y! = X Cxy.
• Sabemos que E [Cxy] = Pr (x e y colidem) ≤ 1 / M.
• Assim, na linearidade da expectativa, E [Cx] = Py E [Cxy] <N / M.

Agora temos o seguinte corolário.

Corolário 3. Se H for universal, para qualquer sequência de operações de inserção, pesquisa e exclusão L, nas quais possa haver no máximo M elementos no sistema ao mesmo tempo, o custo total esperado de operações L para uma h aleatória h ∈ H é apenas O (L) (visualização do tempo para calcular h como constantes).

Prova: para qualquer operação dada na sequência, seu custo esperado é constante no Teorema 2, portanto o custo total esperado das operações L é O (L) na linearidade da expectativa.

Pergunta: podemos realmente construir um H universal? Se não, então tudo isso é inútil. Felizmente, a resposta é sim.

4.1 Criando uma família de hash universal: método de matriz

Suponha que as chaves tenham bits em u. Digamos que o tamanho da tabela M seja igual ao grau 2; portanto, o índice é b-bit longo com M = 2b.

O que faremos é escolher h como a matriz aleatória 0/1 b-por-u e definir h (x) = hx, onde adicionamos o mod 2. Essas matrizes são curtas e grossas. Por exemplo:



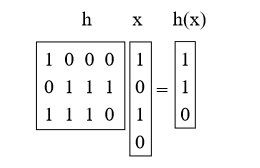
Proposição 4. Para x! = Y Prh [h (x) = h (y)] = 1 / M = 1 / 2b.

Prova: primeiro, o que significa multiplicar h por x? Podemos pensar nisso como adicionar algumas das colunas h (fazendo adição de vetor mod 2), em que 1 bit em x indica quais adicionar. (por exemplo, adicionamos a primeira e a terceira colunas de h acima)

Agora pegue um par de chaves arbitrário x, y tal que x! = Y. Eles devem ser diferentes em algum lugar, de modo que, digamos, sejam diferentes na i-ésima coordenada e, quanto à concretização, dizemos xi = 0 e yi = 1. Imagine que primeiro selecionamos todos h, exceto a i-ésima coluna. Para as demais amostras da i-ésima coluna, h (x) é corrigido. Entretanto, cada uma das 2b configurações diferentes da i-ésima coluna fornece um valor diferente de h (y) (em particular, toda vez que giramos um pouco nessa coluna, transformamos o bit correspondente em h (y)). Portanto, há exatamente uma chance de 1 / 2b de h (x) = h (y).

Existem outros métodos para construir famílias de hash universais, que também se baseiam na multiplicação de números primos (consulte a Seção 6.1).

A próxima pergunta que consideraremos: se corrigirmos o conjunto S, podemos encontrar uma função de hash h de modo que todas as pesquisas tenham tempo constante? A resposta é sim, e isso leva ao tópico do hash perfeito.

5. Hash perfeito

Dizemos que uma função de hash é ideal para S se todas as pesquisas ocorrerem em O (1). Aqui estão duas maneiras de criar funções hash perfeitas para um determinado conjunto S.

5.1 Método 1: uma solução no espaço O (N2)

Digamos que queremos ter uma tabela cujo tamanho seja quadrático no tamanho N do nosso dicionário S. Então, aqui está um método simples para construir uma função hash ideal. Seja H universal e M = N2. Em seguida, basta escolher um h aleatório de H e experimentá-lo! A afirmação é de que há pelo menos 50% de chance de ela não ter colisões.

Proposição 5. Se H é universal e M = N2, então Prh∼H (sem colisões em S) ≥ 1/2.

Prova:

• Quantos pares (x, y) existem em S? A resposta é:
• Para cada par, a probabilidade de colisão é ≤ 1 / M, por definição de universalidade.
• Então Pr (há uma colisão) ≤ / M <1/2.

É como o outro lado do "paradoxo do aniversário". Se o número de dias for muito maior que o número de pessoas ao quadrado, há uma chance razoável de que nenhum casal tenha o mesmo aniversário.

Então, escolhemos um h aleatório de H e, se surgirem colisões, escolhemos um novo h. Em média, precisaremos fazer isso apenas duas vezes. Agora, e se quisermos usar apenas o espaço O (N)?

5.2 Método 2: uma solução no espaço O (N)

A questão de saber se é possível obter um hash perfeito no espaço O (N) está aberta há algum tempo: "As tabelas devem ser classificadas?" Ou seja, para um conjunto fixo, você pode obter um tempo de pesquisa constante apenas com espaço linear? Houve uma série de tentativas cada vez mais complexas, até que finalmente foi resolvido usando a boa idéia de funções de hash universais em um esquema de dois níveis.

O método é o seguinte. Primeiro, vamos fazer o hash em uma tabela de tamanho N usando o hash universal. Isso levará a algumas colisões (a menos que tenhamos sorte). No entanto, refazemos novamente cada cesta usando o método 1, ajustando o tamanho da cesta para obter zero colisão. Assim, o esquema consiste no fato de termos uma função de hash do primeiro nível he uma tabela A do primeiro nível, e então N funções de hash do segundo nível h1, ..., hN e N da tabela de segundo nível A1, ..., A.N ... Para encontrar o elemento x, primeiro calculamos i = h (x) e depois encontramos o elemento em Ai [hi (x)]. (Se você fez isso na prática, poderá definir o sinalizador para que você dê o segundo passo apenas se realmente houver conflitos com o índice i, caso contrário, você apenas colocaria o próprio x em A [i], mas vamos não vamos nos preocupar com isso aqui.)

Digamos que uma função hash hashes n elementos de S no local i. Já provamos (analisando o método 1) que podemos encontrar h1, ..., hN, de modo que o espaço total usado nas tabelas secundárias é Pi (ni) 2. Resta mostrar que podemos encontrar uma função de primeiro nível h de modo que Pi (ni) 2 = O (N). De fato, mostraremos o seguinte:

Teorema 6. Se escolhermos o ponto inicial h do conjunto universal H, então

Pr[X i (ni)2 > 4N] < 1/2. 

Prova. Vamos provar isso mostrando que E [Pi (ni) 2] <2N. Isso implica o que queremos da desigualdade de Markov. (Se houvesse uma probabilidade de até 1/2 de que a soma pudesse ser superior a 4N, apenas esse fato significaria que a expectativa deveria ser superior a 2N. Portanto, se a expectativa for menor que 2N, a probabilidade de falha deverá ser menor. 1/2.)

Agora, o truque mais complicado é que uma maneira de calcular esse valor é contar o número de pares ordenados que têm uma colisão, incluindo colisões consigo mesmo. Por exemplo, se a cesta tiver {d, e, f}, d terá um conflito com cada um de {d, e, f}, e terá um conflito com cada um de {d, e, f} ef terá um conflito com cada um de {d, e, f}, obtemos 9. Então, temos:

 E[X i (ni)2] = E[X x X y Cxy] (Cxy = 1 if x and y collide, else Cxy = 0) = N +X x X y6=x E[Cxy] ≤ N + N(N − 1)/M (where the 1/M comes from the definition of universal) < 2N. (since M = N) 

Então, apenas tentamos um h aleatório de H até encontrarmos um tal que Pi n2 i <4N e, em seguida, corrigindo essa função h, encontramos N funções hash secundárias h1, ..., hN, como no método 1.

6. Discussão adicional

6.1 Outro método de hash universal

Aqui está outro método para construir funções hash universais, que é um pouco mais eficiente do que o método matricial fornecido anteriormente.

No método matricial, consideramos a chave como um vetor de bits. Nesse método, consideraremos a chave x como um vetor de números inteiros [x1, x2, ..., xk] com o único requisito de que cada xi esteja no intervalo {0, 1, ..., M-1}. Por exemplo, se tivermos hash de comprimento k, xi pode ser o i-ésimo caractere (se o tamanho da nossa tabela for pelo menos 256) ou o i-ésimo par de caracteres (se o tamanho da nossa tabela for pelo menos 65536). Além disso, exigiremos que o tamanho da nossa tabela M seja primo. Para selecionar a função hash h, selecionamos k números aleatórios r1, r2, ..., pk de {0, 1, ..., M - 1} e determinamos:

 h(x) = r1x1 + r2x2 + . . . + rkxk mod M. 

A prova de que esse método é universal é construída da mesma maneira que a prova do método da matriz. Seja x e y duas chaves diferentes. Queremos mostrar que Prh (h (x) = h (y)) ≤ 1 / M. Dado que x! = Y, deve haver um caso em que exista algum índice i tal que xi! = Yi. Agora imagine que você selecionou primeiro todos os números aleatórios rj para j! = I. Seja h ′ (x) = Pj6 = i rjxj. Então, escolhendo ri, obtemos h (x) = h ′ (x) + rixi. Isso significa que temos um conflito entre x e y exatamente quando

 h′(x) + rixi = h′(y) + riyi mod M, or equivalently when ri(xi − yi) = h′(y) − h′(x) mod M. 

Como M é primo, a divisão por um valor diferente de zero do mod M é válida (todo número inteiro de 1 a M -1 tem um módulo inverso multiplicativo M), o que significa que existe exatamente um valor ri módulo M para o qual a equação acima é válida verdadeiro, ou seja, ri = (h ′ (y) - h ′ (x)) / (xi - yi) mod M. Portanto, a probabilidade desse incidente é exatamente 1 / M.

6.2 Outros usos do hash

Suponha que tenhamos uma longa sequência de elementos e queremos ver quantos elementos diferentes estão na lista. Existe uma boa maneira de fazer isso?

Uma maneira é criar uma tabela de hash e, em seguida, fazer uma passagem pela sequência, pesquisando cada elemento e inserindo se ainda não estiver na tabela. O número de elementos individuais é simplesmente o número de inserções.

E agora, e se a lista for realmente grande e não tivermos um local para armazená-la, mas uma resposta aproximada for adequada para nós. Por exemplo, imagine que somos um roteador e observe quantos pacotes passam e queremos (aproximadamente) ver quantos endereços IP de origem diferentes existem.

Aqui está uma boa idéia: digamos que temos uma função hash h que se comporta como uma função aleatória e imaginemos que h (x) é um número real de 0 a 1. Uma coisa que podemos fazer é acompanhar o mínimo o valor do hash foi produzido até o momento (portanto, não teremos uma tabela). Por exemplo, se as chaves são 3,10,3,3,12,10,12 eh (3) = 0,4, h (10) = 0,2, h (12) = 0,7, obtemos 0, 2)

O fato é que, se selecionarmos N números aleatórios em [0, 1], o valor mínimo esperado será 1 / (N + 1). Além disso, há uma boa chance de que ele esteja bem próximo (podemos melhorar nossa estimativa executando várias funções de hash e medindo a mediana dos mínimos).

Pergunta: por que usar uma função hash, e não apenas escolher um número aleatório toda vez? Isso ocorre porque nos preocupamos com o número de elementos diferentes, e não apenas com o número total de elementos (esse problema é muito mais simples: basta usar um contador ...).

Amigos, este artigo foi útil para você? Escreva nos comentários e participe do dia aberto , que será realizado no dia 25 de abril.