👩🏿‍⚕️ 🌁 ♀️ Mas não acenamos para a comunicação óptica? Lasers, espaço, CubeSat 🍒 🧗🏼 ✋🏼

O material descrito abaixo é o resultado de um trabalho conjunto com os professores da TU Ilmenau como parte de um projeto de curso local (Projeto de Pesquisa Avançada). A experiência é interessante, mas não sem certas dificuldades. Nós fizemos esse projeto (e mais um) junto com minha então noiva - sim, então tivemos a sorte de estudar juntos e fazer um estágio na Alemanha. Na verdade, foi ela quem fez essa parte do trabalho em maior medida, mas eu quero popularizar esse tópico.

Então, um dia, marcamos uma consulta para escolher um tópico para o trabalho científico ...

Fundo curto (em rostos)

Professor de alemão # 1 : Oh, eu ouvi você estudar os satélites CubeSat lá em casa?

Eu e minha futura esposa : Bem, você poderia dizer que ...

N.p. No. 1 : Ótimo! Mas e se você tentar considerar a comunicação óptica entre satélites? Sei que, em alguns casos, a óptica oferece o melhor desempenho energético, para satélites tão pequenos, presumo que esse problema seja muito importante. Eu tenho um amigo profissionalmente envolvido em óptica sem fio. Eu acho que será um projeto interessante!

Nós : Parece interessante!

(algum tempo passa)

Encontro com um professor de alemão número 2 .

N.p. No. 2 : Sim, tudo isso, é claro, é ótimo, mas que tipo de satélites? Uma massa tão pequena? Eles podem se comunicar? Quem sugeriu isso? Entendido ... Aparentemente, não o veremos nessas reuniões. Vá procurar exemplos do mundo real - ainda não acredito.

E partimos ...

E, para sua alegria, eles até encontraram um artigo inteiro dedicado a esse tópico. Uma diferença importante era que a comunicação através da óptica deveria estar com a Terra, e não entre satélites. Isso é muito importante porque:

todos os tipos de dispersão e interferência, é claro, neste caso mais,
no entanto, o receptor na Terra pode ser ajustado o suficiente e o transmissor é bastante preciso. E o segmento espacial, você entende, complica um pouco as coisas.

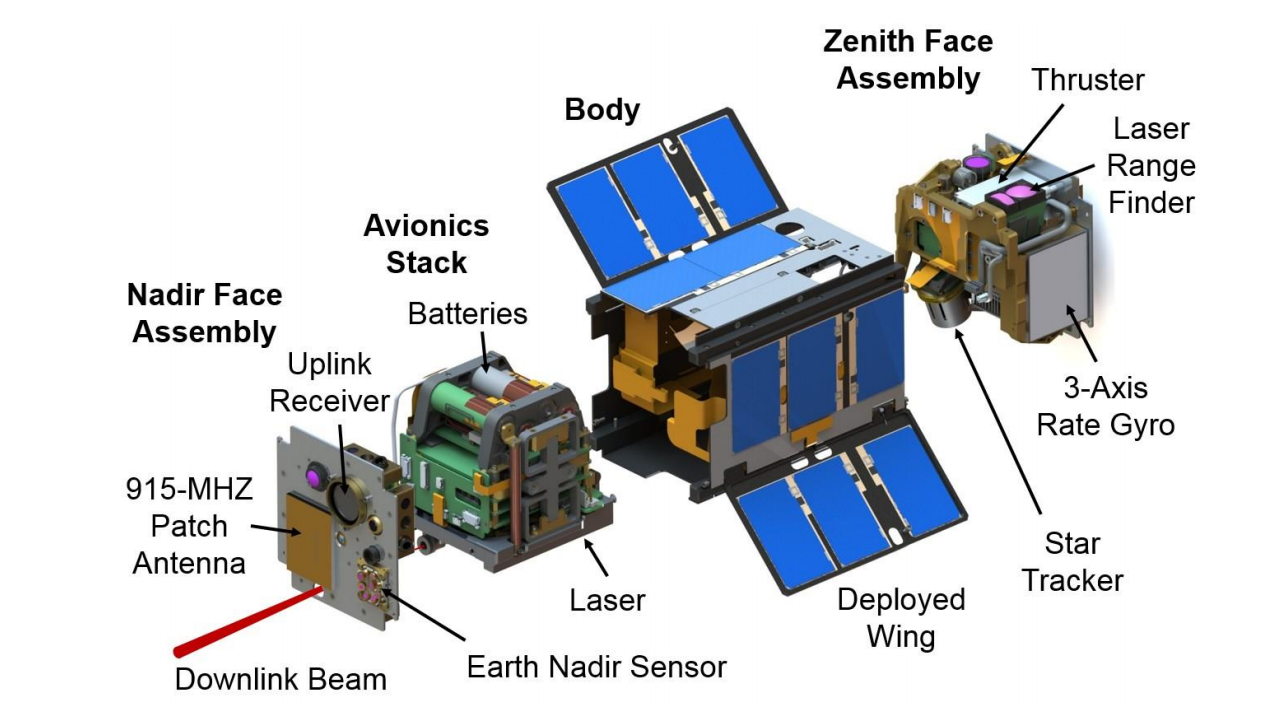
Fig. 1. Representação esquemática do nanossatélite AeroCube-OCSD [1].

Mas isso já era algo, e marcamos uma consulta novamente.

N.p. No. 2 : Bem, bem, desde a NASA ... Vamos tentar calcular o orçamento de energia e compará-lo com o orçamento de energia do link de rádio. Artigos relacionados para jogar fora?

E ele descartou seu artigo [2] (vou me referir a ele várias vezes hoje) e alguns artigos de outros autores para uma compreensão geral da questão.

O que implica o orçamento de energia da linha óptica inter-satélite?

Orçamento de energia óptica sem fio

Mas implica, por si só, em geral, o mesmo que o habitual (potência necessária do transmissor, potência recebida, SNR, etc.) - apenas os ruídos são considerados um pouco mais interessantes do que no caso das radiocomunicações ...

Vamos começar a modelar - será um pouco mais claro:

import numpy as np from matplotlib.pyplot import plot, grid, xlabel, ylabel, legend import matplotlib.pyplot as plt from scipy import special

Suponha que tenhamos um sistema assim:

 #initial parameters for optical case R = 100*1e3 #distance between objects, eg satellites, in m (100 km) Bit_rate = 1e6 #bit rate (1 Mbps) h = 6.62607004*1e-34 # Planck constant c = 299792458 #speed of light wavelength_opt = 1550*1e-9 #optical wavelength freq_opt = c/wavelength_opt #optical frequency Ptx_opt = 1 #transmitter power in Watts Ptx_opt_dBm = 10*np.log10(Ptx_opt*1e3) #transmitter power in dBm

Definimos um certo conjunto de possíveis diâmetros de receptores ópticos (de fato, lentes) - lembramos as restrições sobre o tamanho dos próprios satélites:

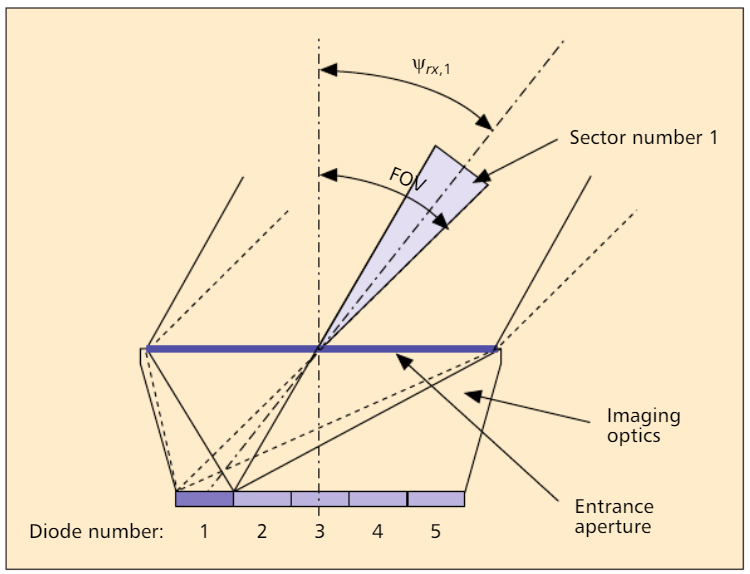
 a = [i for i in range(0,50,5)] a = np.array(a)*1e-3 #diameter of the receiver (in meters) a[0] = 1*1e-3 a_m = a*100 # for figures (in cm)

Fig. 2. Diagrama esquemático de um fotodetector: mostrado como um exemplo para o setor n ° 1, cujos ângulos de incidência são exibidos no fotodiodo n ° 1 [2].

E alguns possíveis ângulos de divergência do raio laser (nosso transmissor):

 div_ang = [0.2*1e-3, 0.5*1e-3, 2*1e-3, 5*1e-3, 7*1e-3] div_ang = np.array(div_ang) #half of divergence angle

Fig. 3. Ilustração do ângulo de divergência do raio laser.

A potência na entrada do receptor (potência recebida) pode ser calculada pela fórmula [2] :

$P_ {rx} = \ frac {A_ {rx}} {2 \ pi R ^ 2} \ left (1 - \ frac {ln2} {ln (cos \ theta_ {div})} \ right) P_ {tx} \ quadrante [W]$

onde $A_ {rx} = \ frac {d_ {rx} ^ 2 \ pi} {4}$ É a área da recepção, $d_ {rx}$ - diâmetro da lente receptora, $R$ - distância entre satélites, $\ theta_ {div}$ É metade do ângulo de divergência e $P_ {tx}$ - potência transmitida.

 Prx_opt_dBm = np.zeros((len(div_ang), len(a))) Prx_opt = np.zeros((len(div_ang), len(a))) Pathloss_dBm = np.zeros((len(div_ang), len(a))) Pathloss = np.zeros((len(div_ang), len(a))) Arx_m2 = (np.pi/4)*(a**2) for f, dvangl in enumerate(div_ang): #received power Prx_opt[f,:] = (Ptx_opt*Arx_m2)/ (2*np.pi*(R**2))\ *(1-(np.log(2)/np.log(np.cos(dvangl)))) Prx_opt_dBm[f,:] = 10*np.log10(Prx_opt[f,:]*1e3) #path loss Pathloss[f,:] = (Arx_m2)/(2*np.pi*(R**2))\ *(1-(np.log(2)/np.log(np.cos(dvangl)))) Pathloss_dBm[f,:] = 10*np.log10(Pathloss[f,:]*1000)

Ok, algo já está lá. Mas quanto é tudo isso fisicamente realizável?

Limitações de sensibilidade

Limites quânticos

Lembre-se da fórmula de energia do fóton:

$E = hf \ quad \ esquerda [m ^ 2 kg / s ^ 2 \ direita]$

onde $h$ = 6.62607004e-34 $m ^ 2 kg / s$ A constante de Planck e $f$ - frequência portadora (Hz).

Isto será seguido por uma pequena heurística extraída de nossas consultas. Se alguém conhece uma justificativa ou refutação teórica - compartilhe!

Energia necessária (energia mínima por bit de informação no lado do receptor para detectar pelo menos algo):

$E_ {req, Q} = N_ {ph} hf \ quad \ esquerda [m ^ 2 kg / s ^ 2 \ right]$

onde $N_ {ph}$ - o número médio de fótons necessários para detectar 1 bit de informação.

Energia teórica para um pulso óptico:

 E_theor = 10*h*freq_opt

Um valor de energia mais realista para um pulso óptico (diodo APD ):

 E_real_APD = 1000*h*freq_opt

Um valor de energia mais realista para um pulso óptico (diodo PIN ):

 E_real_PIN = 10000*h*freq_opt

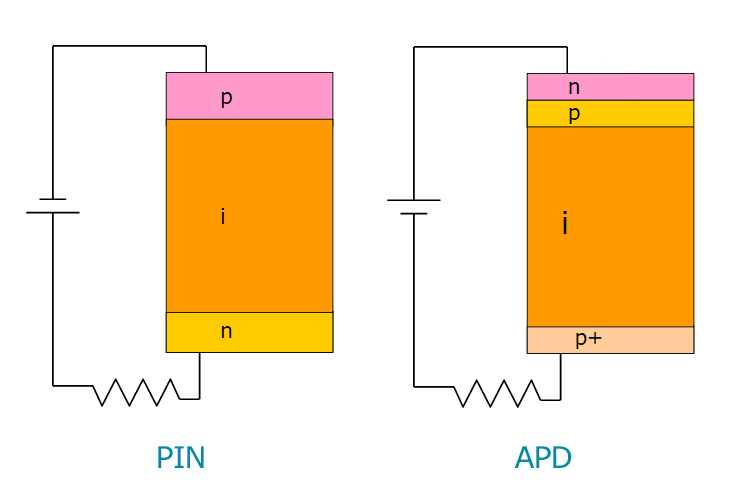
Fig. 4. O circuito dos fotodiodos em consideração.

Necessário (mínimo) recebe potência (sensibilidade máxima):

$P_ {req, Q} = 10 \ log_ {10} \ left (\ frac {E_ {req, Q} B} {10 ^ {- 3}} \ right) = 10 \ log_ {10} \ left (\ frac {E_ {req, Q} R_b} {10 ^ {- 3}} \ right) \ quad [dBm]$

onde $B$ A largura de banda do canal de comunicação e $R_b$ É a taxa de bits.

 P_req_theor = 10*np.log10(E_theor*Bit_rate*1000) P_req_real_APD = 10*np.log10(E_real_APD*Bit_rate*1000) P_req_real_PIN = 10*np.log10(E_real_PIN*Bit_rate*1000)

Mas isso não é tudo: a modulação também faz sua contribuição limitadora.

Limites de probabilidade de erro

Como ponto de partida, consideraremos a modulação OOK (On-off Keying).

Fig. 5. Ilustração do princípio da modulação OOK.

A probabilidade de erros ( BER ) para isso será [2]:

$P_b = \ frac {1} {2} ercf \ left (\ sqrt {\ frac {SNR} {2}} \ right) = \ frac {1} {2} ercf \ left (\ sqrt {\ frac {P_ { req} ^ 2 \ gama ^ 2} {2 \ sigma ^ 2}} \ right)$

onde $SNR$ A relação sinal / ruído é $\ sigma ^ 2$ A variação do ruído (ou seja, a potência do ruído) e $\ gama$ É a sensibilidade dos fotodiodos ( responsividade do fotodiodo ).

BER para OOK (diodo PIN):

$P_ {b, PIN} = \ frac {1} {2} ercf \ left (\ frac {\ gama P_ {req, PIN}} {\ sqrt {2 \ sigma_ {PIN} ^ 2}} \ right)$

E portanto:

$P_ {req, PIN} = \ frac {erfcinv (2P_b) \ sqrt {2 \ sigma_ {PIN} ^ 2}} {\ gamma} \ quad [W]$

BER para OOK (diodo APD):

$P_ {b, APD} = \ frac {1} {2} ercf \ left (\ frac {\ gama M P_ {req, APD}} {\ sqrt {2 \ sigma_ {APD} ^ 2}} \ right)$

E portanto:

$P_ {req, APD} = \ frac {erfcinv (2P_b) \ sqrt {2 \ sigma_ {APD} ^ 2}} {\ gamma M} \ quad [W]$

onde $M$ - Este é um ganho de referência.

Potência de ruído

Como você deve ter adivinhado, os ruídos também serão calculados de maneira um pouco diferente.

Potência de ruído para o diodo PIN

O ruído térmico pode ser calculado pela fórmula [3, p 11] :

$\ sigma_ {PIN} ^ 2 = \ left (\ frac {4kT} {R_f} + 2qI_ {BE} \ right) I_2R_b = N_0 + 2qI_ {BE} I_2R_b \ quad [W]$

onde $T = 290 K$ , $k = 1.38064852e-23$ - constante de Boltzmann $R_f = \ frac {100} {2 \ pi C_d R_b}$ - resistência direta $C_d$ - capacidade de fotodíodos, $q$ É a carga de um elétron, $I_ {BE} = \ frac {I_C} {\ beta}$ - corrente do emissor base (emissor base ou corrente de fuga ou polarização ), $I_2$ - o valor da integral Personick (- desisto, não encontrei uma tradução adequada, por favor me diga) para ruído térmico, $R_b$ - taxa de bits $N_0$ - densidade espectral do ruído.

 Cd = 2*1e-12 #capacitance of the photodiode T = 290 #absolute temperature Rf = 100/(Cd*2*np.pi*Bit_rate) #photodiode resistance k = 1.38064852*1e-23 #Bolzman constant I2 = 0.562 #depends on filter (Personick integral) for match filter q = 1.60217662*1e-19 #electron charge Ibe = (0.25*1e-3)/200 #RESULT thermal_Noise_variance_add = 2*q*Ibe*I2*Bit_rate N_0 = 4*k*T/Rf #thermal noise density for PIN thermal_Noise_variance = N_0*Bit_rate*I2

Potência de ruído para o diodo APD

Prepare- se para este diodo - muitas letras latinas:

$\ sigma_ {APD} ^ 2 = \ frac {4kT} {R_f} I_2R_b + 2qI_dM_ {Si} ^ 2F_ {Si} I_2R_b = N_0 + 2qI_2R_b (I_ {BE} + M_ {Si} ^ 2F_ {Si} I_d) \ aprox N_0 + 2qI_2I_dR_bM_ {Si} ^ 2F_ {Si} \ quad [W]$

onde $I_d$ - corrente escura (corrente escura), $M_ {Si}$ É um ganho típico (silício), $F_ {Si}$ - o fator de excesso de ruído.

Os parâmetros são recolhidos do seguinte:

Este documento não leva em consideração o ruído do transistor de efeito de campo de entrada (ruído FET de entrada) e o ruído de carga do transistor de efeito de campo de entrada (ruído da carga FET de entrada). Leia mais sobre esses termos em [3, p 15] .

 Id = 0.05*10e-9 #dark current (500e-12) M_Si = 100 #typical gain F_Si = 7.9 #excess noise factor apd_noise_Si = 2*q*Id*I2*Bit_rate*(M_Si**2)*F_Si #noise

Modelagem

Poder recebido

Substituímos tudo que foi esclarecido em nossas fórmulas:

 r = 0.53 #A/W photodiode responsivity Pb = 10e-9 #Bit error rate (BER) P_req_pin = 10*np.log10((special.erfcinv(2*Pb)* np.sqrt(2*(thermal_Noise_variance+thermal_Noise_variance_add))/(r))*1e3) #in dBm P_req_apd_lin = special.erfcinv(2*Pb)*np.sqrt(2*(thermal_Noise_variance+apd_noise_Si))/(r*M_Si) P_req_apd = 10*np.log10(P_req_apd_lin*1e3) #in dBm fig = plt.figure(figsize=(10, 7), dpi=300) req_theor = np.ones((len(a_m),))*P_req_theor req_real_APD = np.ones((len(a_m),))*P_req_real_APD req_real_PIN = np.ones((len(a_m),))*P_req_real_PIN PIN = np.ones((len(a_m),))*P_req_pin APD = np.ones((len(a_m),))*P_req_apd a_m = a_m.reshape((10,)) plot(a_m, Prx_opt_dBm[0,:],'-o', label = '0.2 mrad') plot(a_m, Prx_opt_dBm[1,:],'-o', label = '0.5 mrad') plot(a_m, Prx_opt_dBm[2,:],'-o', label = '2 mrad') plot(a_m, Prx_opt_dBm[3,:],'-o', label = '5 mrad') plot(a_m, Prx_opt_dBm[4,:],'-o', label = '7 mrad') plot(a_m, req_theor,'k--', label = 'Sensitivity limit (theory)') plot(a_m, req_real_APD, '--*', label = 'Sensitivity limit (APD)') plot(a_m, req_real_PIN, '--', label = 'Sensitivity limit (PIN)') plot(a_m, APD, '-*',label = '1e-9 OOK BER limit (APD)') plot(a_m, PIN, label = '1e-9 OOK BER limit (PIN)') plt.gca().invert_yaxis() xlabel('Rx diameter (cm)'); ylabel('Prx and Preq (dBm)') legend() grid() plt.show()

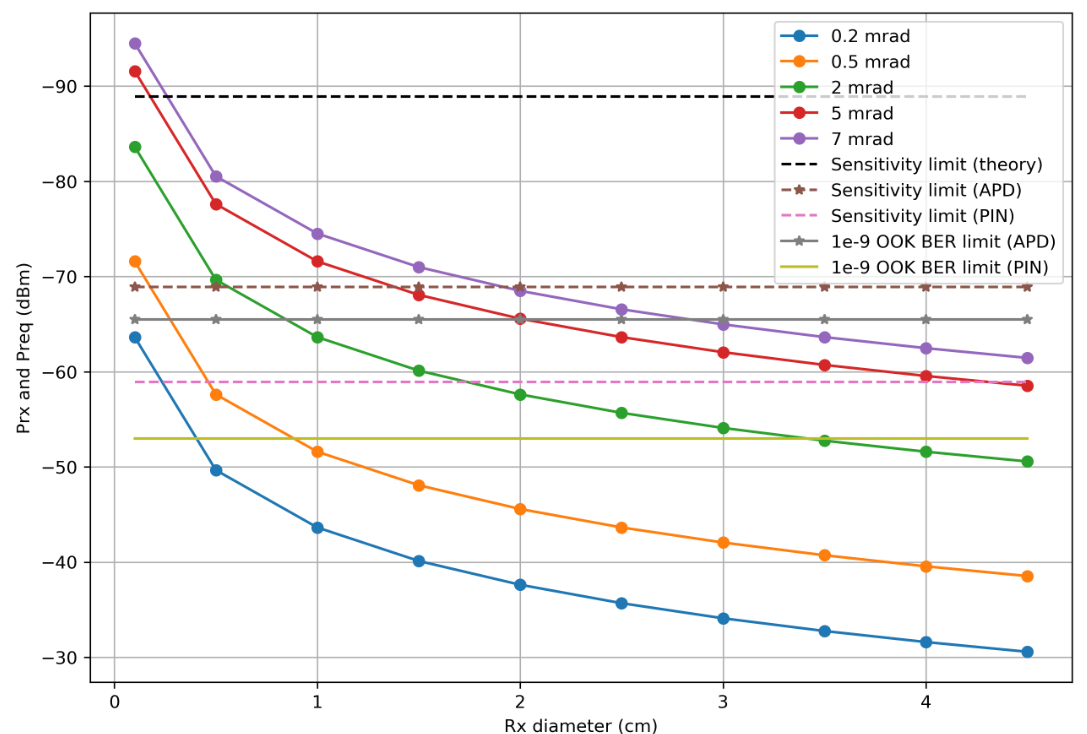
Vamos explicar: você precisa observar as partes das curvas que ficam abaixo das linhas horizontais correspondentes.

Potência transmitida

E agora vejamos o problema oposto: consertamos um pouco de energia no lado receptor e vemos que tipo de energia precisará ser aplicado no lado transmissor:

$P_ {tx, dBm} = P_ {rx, dBm} + | L | + | L_ {add} |$

onde $L = 10 \ log_ {10} \ left [\ frac {A_ {rx}} {2 \ pi R ^ 2} \ left (1 - \ frac {ln2} {ln (cos \ theta_ {div})} \ right ) \ right]$ A atenuação do caminho e $L_ {add}$ - Essa é uma margem para perdas.

 Prx_req_dB_APD = -65.5 Prx_req_dB_PIN = -52.9 margin = 5 Arx_m2 = np.zeros((len(a))) Ptx_variable_APD = np.zeros((len(div_ang), len(a))) Ptx_variable_PIN = np.zeros((len(div_ang), len(a))) #area rx Arx_m2 = (np.pi/4)*(a**2) for f, dvangl in enumerate(div_ang): #Ptx required Ptx_variable_APD[f,:] = Prx_req_dB_APD + np.abs(Pathloss_dBm[f,:]) + margin; Ptx_variable_PIN[f,:] = Prx_req_dB_PIN + np.abs(Pathloss_dBm[f,:]) + margin; fig = plt.figure(figsize=(10, 7), dpi=300) plot(a_m, Ptx_variable_APD[0,:],'-o', label = 'APD, 0.2 mrad') plot(a_m, Ptx_variable_PIN[0,:],'-*', label = 'PIN, 0.2 mrad') plot(a_m, Ptx_variable_APD[1,:],'-o', label = 'APD, 0.5 mrad') plot(a_m, Ptx_variable_PIN[1,:],'-*', label = 'PIN, 0.5 mrad') plot(a_m, Ptx_variable_APD[2,:],'-o', label = 'APD, 2 mrad') plot(a_m, Ptx_variable_PIN[2,:],'-*', label = 'PIN, 2 mrad') xlabel('Rx diameter (cm)'); ylabel('P_tx (dBm)') legend() grid() plt.show()

Uma comparação com o caso do canal inter-satélite eletromagnético pode ser encontrada em nosso artigo de periódico . Também descreve as razões pelas quais, no final, recusamos esse cenário, mas vou falar mais sobre isso aqui.

Armadilhas

E aqui estamos, agredidos por livros de referência e fórmulas matemáticas, mas, no entanto, inspirados pelos resultados obtidos (sim, o que existe - pelo próprio fato de belos gráficos!), Estamos fazendo uma reunião final antes da defesa. E nos deparamos com uma nova rodada de detalhes importantes ...

N.p. No. 2 : Bem, bem, está claro que existem ganhos. Eles convenceram que já existe algum tipo de base de hardware. E a segmentação? Você provavelmente já ouviu falar sobre o sistema PAT ( P ointing, A cquisition e T racking).

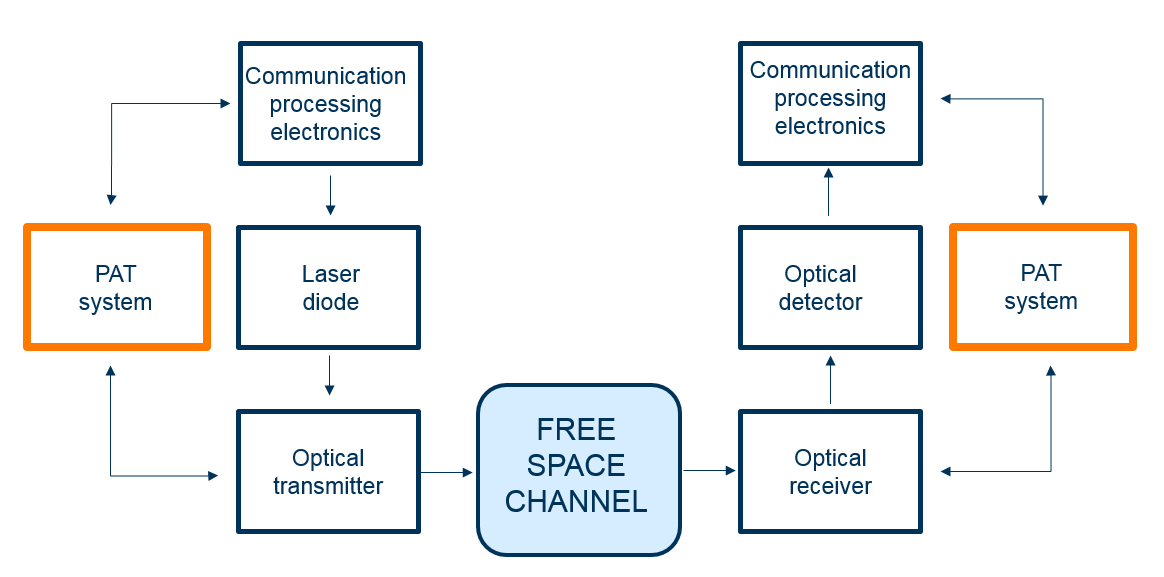
Fig. 6. Um diagrama simplificado de um sistema transceptor óptico sem fio.

N.p. No. 2 : Sim, existem exemplos de canais ópticos para satélites grandes [4] , no entanto, nesse caso, você pode oferecer um diâmetro maior do receptor, um ângulo maior de divergência do laser e uma potência de transmissão mais alta. Além disso, acho que o próprio CubeSat vibra muito quando se move . Para um canal de rádio em frequências relativamente baixas, isso pode não ser essencial para a ótica - você mesmo entende. Existe um sistema de estabilização e PAT tão preciso no momento?

E nós fomos muito atenciosos ...

N.p. No. 2 : É isso que, da minha parte, faço uma avaliação positiva. No entanto, meu conselho para você: desça do céu à terra ...

E nós, exaustos, caímos: decidimos não continuar o projeto com a óptica de satélite. Além disso, mesmo durante nossas freqüentes reuniões, acumulamos algum desgaste ...

No entanto, não, não, e até mesmo uma nota de esperança do aluno se insinua no coração de que o professor estava errado em seu ceticismo. Não, não, e quero encontrar o próprio conceito nas realizações da tecnologia moderna. E o olhar sobe para cima ...

Literatura

Janson SW, Welle RP O programa de demonstração de sensores ópticos e comunicações da NASA: uma atualização // 28ª Conferência Anual da AIAA / USU sobre pequenos satélites. - 2014 .-- S. 4-7.
Wolf, M. & Kreß, D. (2003). Transmissão por infravermelho sem fio de curto alcance: o link buoget comparado ao RF . Comunicações sem fio IEEE, 10 (2), 8-14.
https://www.nii.ac.jp/qis/first-quantum/forStudents/lecture/pdf/noise/chapter12.pdf
Smutny B. et al. Link de comunicação entre satélites ópticos de 5,6 Gbps // Tecnologias de comunicação a laser de espaço livre XXI. - Sociedade Internacional de Óptica e Fotônica, 2009.- T. 7199. - S. 719906.

Mas não acenamos para a comunicação óptica? Lasers, espaço, CubeSat