Olá querido leitor! Apresento a você a tradução em inglês do artigo "Physics, The Next Frontier", de Chris Hecker.

Eu, um desenvolvedor iniciante em Java, fui confrontado com o fato de que os materiais para a criação de um mecanismo físico no jogo são apresentados apenas em inglês; portanto, este artigo foi traduzido. Haverá mais três artigos na série, eu os publicarei o mais rápido possível. Boa leitura!

Novas fronteiras em física

Não há dúvida de que todos os anos os gráficos do jogo estão se tornando mais realistas. Hoje em dia, todo mundo cria (ou pelo menos mostra capturas de tela) mundos 3D com mapas de textura e, quando pessoas bastante trabalhadoras se reúnem para trabalhar em um projeto, cada desenvolvedor pode desenhar bilhões de polígonos de texturas e sombras realistas por segundo. Em termos técnicos, o que resta fazer para criar um jogo em alto nível? Todo desenvolvedor com uma cópia do livro "Aprenda a usar o hardware 3D em 21 dias" poderá criar um jogo verdadeiramente impressionante?

Nem um pouco. Desenvolvedores de alto nível continuarão a elevar o padrão em muitas tecnologias diferentes (como complexidade da GUI, inteligência artificial e rede). Claro, tudo isso é muito importante, não podemos discutir seriamente nenhum deles sem especificar detalhes. No entanto, existe uma tecnologia aplicável a tudo que, na minha opinião, se tornará um fator decisivo no futuro próximo: a física.

Considere o seguinte exemplo: você se lembra dessas enormes engrenagens giratórias em um dos primeiros níveis do Duke Nukem 3D?



Figura 1. Captura de tela do jogo "Duke Nukem 3D"

Imagine que sua rotação seria descrita não por animação cíclica, mas por um mecanismo físico real. De repente, as engrenagens se tornam algo mais do que uma decoração de jogo, assim como uma delas se desvia do ângulo determinado e rola pelo corredor atrás de você, como nos filmes de Indiana Jones. Ou imagine que, depois de disparar um equipamento de um lançador de foguetes, ele rolará pelo corredor e esmagará seu amigo, que se arrastou para trás para matá-lo! Motores físicos tornam essas situações reais.

A simulação física é o que faz todo o mundo do jogo: graças a ele, "aqui" está localizado aqui, se você entende o que quero dizer. Qualquer mágica nos gráficos do mundo não permitirá que o jogador mergulhe no processo do jogo se ele se interpenetrar em outro jogador, ou nas paredes do nível, ou se a massa e o momento da massa não forem sentidos. Os animadores da Disney acharam esse sentimento das massas o que separa boa animação de animação ruim. De acordo com o livro épico Disney Animation: The Illusion of Life, de Frank Thomas e Ollie Johnston, os animadores da Disney, mesmo que apenas pendurem um pôster no estúdio, devem sempre se perguntar: “Existe muito peso, profundidade e equilíbrio em seus desenhos?” ? "

Mas hoje quase todo jogo tem um mecanismo de física, certo? Sem dúvida, é isso que evita que seu carro caia sobre o limite do mundo do jogo, graças a isso, seus personagens não voam para o espaço quando pulam, e isso lança seu barco para o lado quando um foguete explode nas proximidades. No entanto, a maioria dos mecanismos físicos nos jogos modernos é bastante fraca. Eles lidam apenas com a tarefa de impedir que o carro caia nos limites do mundo, mas suas capacidades não são suficientes para levar o jogo a um novo nível - onde os destroços de um carro naufragado podem explodir na pista, causando um rolar de paredes e outros carros.

Outros efeitos físicos que muitas vezes são ignorados incluem: desde simples efeitos de torção como resultado de um ataque tangente, até os personagens do jogo mantendo o equilíbrio e se movendo, diferentemente dos animados estaticamente. Acredito que muitos desenvolvedores ignoram essas possibilidades porque não entendem a matemática que descreve a física ou estavam muito ocupados criando mapas de textura para aprendê-la. O ataque de hardware para trabalhar com 3D cuidará desse último, e estou iniciando uma nova série de artigos. O primeiro artigo tratará das formalidades. No final do nosso ciclo, você mesmo poderá criar um mecanismo físico que fará com que os jogadores se sintam completamente imersos na jogabilidade, graças ao realismo incrível ou a um surrealismo divertido, mas persistente.

Atenção! Física = matemática, para concluir um projeto interessante, você terá que usar os dois. Antes que isso assuste você, deixe-me notar que a matemática que descreve a física não é apenas elegante e bonita, mas também tem um caráter aplicado. Ou seja, não é matemática abstrata para matemática. Cada equação que usamos tem um significado físico real. Criamos equações a partir de um modelo físico e, em troca, as equações nos dizem como o modelo se comporta no tempo.

Grande empresa

A física é um amplo campo científico. Mas estamos realmente interessados ​​em sua pequena seção chamada "dinâmica", ou mais precisamente, "dinâmica de sólidos". A dinâmica pode ser definida em termos de uma seção relacionada - cinemática (a doutrina do movimento no tempo). A cinemática não se concentra no que causa o movimento ou em como os corpos acabam onde estão, simplesmente descreve o movimento. A dinâmica, pelo contrário, descreve as forças e massas que contribuem para os valores da cinemática para mudar ao longo do tempo. Até que ponto a bola de beisebol voará se o tempo de vôo for de 10 segundos e sua velocidade inicial for de 50 quilômetros / hora, e a trajetória - uma linha reta - for um problema cinemático; até que ponto a bola de beisebol voará no campo gravitacional da terra, se eu acertar com um taco - este é um problema dinâmico.

A parte da dinâmica que descreve os sólidos refere-se às restrições que adicionamos aos objetos simulados. A forma de um corpo sólido não muda durante a simulação - é mais provável que o corpo seja de madeira ou metal do que gelatinosa. Podemos criar figuras articuladas, por exemplo, de uma pessoa, construindo cada parte da figura a partir de um corpo sólido e criando ligamentos entre elas, mas não contaremos com ossos dobrados sob estresse ou efeitos semelhantes. Isso nos permitirá simplificar nossas equações sem perder a qualidade do interessante comportamento dinâmico dos corpos.

Embora consideremos uma parte tão pequena da dinâmica, a dinâmica de um corpo rígido exigirá uma série de artigos para explicar a essência. Começamos nossa jornada estudando o básico da programação de computadores para descrever o movimento de um corpo rígido plano sob a ação de forças. Repito persistentemente a "programação de computadores", porque, além das equações que escrevemos para cinemática e dinâmica, também aprenderemos como resolver essas equações usando cálculos com números de ponto flutuante, que é vital para todo programador saber. Digo "sólido plano" porque trataremos apenas do mundo bidimensional ao longo do próximo artigo e além. Os princípios - e, de fato, mais do que apenas equações - também podem ser transferidos para o mundo tridimensional, mas definitivamente tudo é muito mais simples no mundo bidimensional, então estudaremos lá até nos sentirmos confiantes em entrar no espaço tridimensional. Em artigos futuros, aprenderemos a descrever o efeito da rotação, o processamento dos contatos dos corpos e, é claro, como fazer tudo isso em um mundo tridimensional. Bem, palavras suficientes! Vamos começar!

Trabalhar com um derivado

Isso pode ser uma surpresa para você, mas você realmente não pode mover um objeto simplesmente empurrando-o. Eu sei, você acha que estou errado em provar o oposto de mim jogando essa revista no lixo por escrever essas bobagens, mas é verdade! Apenas pressionar uma revista nunca afetará diretamente sua posição no espaço. De fato, a pressão nem afeta diretamente sua velocidade. O que a pressão realmente afeta é a aceleração da revista e, de fato, é uma das conclusões mais importantes da história da ciência.

Para usar esse fato para fazer algo interessante, precisamos primeiro falar sobre a relação da posição do corpo com velocidade e aceleração. De fato, todos esses valores estão intimamente relacionados (como você provavelmente sabe): a velocidade é um indicador de mudanças nas coordenadas do corpo ao longo do tempo e a aceleração é um indicador de mudanças na velocidade. A principal ferramenta para estudar mudanças nessas quantidades ao longo do tempo é o cálculo diferencial. Se você entende isso, seguimos em frente. Suponho que você seja bom em matemática. Usaremos apenas cálculos escalares e vetoriais simples (derivadas e integrais), mas não será supérfluo se você estiver familiarizado com a matemática como um todo. Para referência: meu livro favorito sobre computação é Cálculo com Geometria Analítica, de Thomas e Finney.

Coordenada, velocidade e aceleração são cinemáticas que serão discutidas neste artigo. A localização de um sólido em um mundo bidimensional é, obviamente, um par de coordenadas X e Y, que denotam as coordenadas do espaço de um determinado ponto do corpo. A derivada do vetor de coordenadas é o vetor de velocidade, e nos mostra em qual direção o ponto está se movendo (e o corpo, se ignorarmos a rotação, o que está acontecendo agora) e a velocidade com que ele está se movendo. O cálculo vetorial é apenas o cálculo escalar de cada elemento do vetor; portanto, a derivada da coordenada X é a velocidade do corpo em relação a X, e assim por diante. Apresentamos a seguinte notação. Seja a coordenada do corpo o vetor r, e a velocidade seja o vetor v ou o vetor r com um primo. Nós obtemos a equação:

$$

$${{dx} \ over {dt}} = v = r '$$

Equação 1

Se diferenciarmos o vetor de velocidade em relação ao tempo, isso mostrará como o vetor de coordenadas muda com o tempo. A aceleração é determinada por analogia. Esta é a primeira derivada da velocidade ou a segunda derivada do vetor de coordenadas:

$$

$${{d ^ 2 r} \ over {dt ^ 2}} = r '' = {{dr '} \ over {dt}} = {{dv} \ over {dt}} = v' = a$$

Equação 2

A integral da aceleração nos dará velocidade e, integrando a aceleração duas vezes, obtemos a coordenada.

Essas relações na cinemática mostram que podemos encontrar a aceleração de um objeto, podemos integrá-lo ao longo do tempo para obter velocidade e coordenar. Como veremos mais adiante, passaremos à integração muitas vezes em nosso código de simulação e calcularemos uma nova posição para o nosso sólido para cada quadro. Viva animação!

Aqui está um exemplo simples para um mundo unidimensional que podemos integrar analiticamente. Vamos concordar que queremos encontrar a alteração de coordenadas do final do último quadro para a hora do quadro atual para desenhar a posição atual. Em seguida, dizemos que a aceleração do nosso sólido foi igual a 5 unidades arbitrárias / segundo ^ 2. Usaremos o tempo decorrido desde o final do último quadro como uma variável t (no elemento de integração dt).

$$

$$v (t) = cidade = 5dt = 5t + C$$

Equação 3

As equações acima mostram que a velocidade é uma função do tempo decorrido desde o último quadro. Encontramos a constante de integração C, que é igual à velocidade inicial no início do período de integração (em t = 0).

$$

$$v (0) = 5 (0) + C$$

$$

$$v_0 = {C}$$

Equação 4

$$

$$v (t) = 5t + v_0 {}$$

Agora integramos nossa equação de velocidade para encontrar a coordenada (novamente, não se esqueça da constante de integração):

$$

$$r (t) = ∫v (t) dt = t5t + v_0 dt = {{5} \ over {2}} t ^ 2 + v_0 t + r_0$$

Equação 5

Com base na Equação 5, podemos encontrar a posição atual apenas por uma determinada aceleração se conhecermos a coordenada e a velocidade iniciais (que serão obtidas no último quadro) e o tempo decorrido. A variável de entrada é time, e o valor da função é a posição atual. Também indicaremos o tempo na Equação 4 para calcular a velocidade final, para que possamos usá-la como condição inicial para o próximo quadro.

Que a força esteja com você

Agora, percebemos que precisamos definir a aceleração corretamente para integrar as equações cinemáticas, a fim de obter a animação. A saída dos alto-falantes no palco. Lembra, como eu disse, ao pressionar alguma coisa, você afeta diretamente apenas a aceleração do corpo? Bem, “exercer pressão” é apenas um eufemismo para a frase “aplicar força” - uma das duas principais variáveis ​​da dinâmica - e agora podemos recorrer a Newton para descobrir como as forças afetam a aceleração. A segunda lei de Newton conecta a força F com a derivada da massa - a segunda magnitude da dinâmica - vezes a velocidade. O produto de massa e velocidade é chamado de "momento do corpo", denotado por p:

$$

$$F = p '= {{dp} \ over {dt}} = {{d (mv)} \ over {dt}} = mv' = ma$$

Equação 6

A massa é uma constante para as velocidades com as quais estamos trabalhando agora, isso segue a derivada na Equação 6, e obtivemos a conhecida equação F = ma (embora eu tenha certeza de que Newton determinou inicialmente a força através da derivada do momento).

Se estivéssemos lidando apenas com pontos materiais, a Equação 6 é o que precisamos em dinâmica. Para uma dada força de um dado ponto material, a aceleração é encontrada dividindo a força pela massa. Isso nos dá aceleração, o que ajudará a resolver a equação de movimento do exemplo acima. No entanto, estamos lidando com sólidos com massa distribuída em uma determinada área (volume, quando se trata do mundo tridimensional), então ainda precisamos trabalhar.

Primeiro, considere um sólido como um conjunto de massas pontuais. Definiremos o momento total, pT, para um sólido, como a soma do momento de todos os pontos que compõem o corpo (eu uso a indexação superior, porque quero mostrar mais claramente quais valores quantitativos pertencem a esses pontos):

$$

$$p ^ T = \ sum_ {i} {m ^ i v ^ i}$$

Equação 7

Podemos simplificar bastante a análise da dinâmica de um corpo rígido, introduzindo o conceito de centro de massa (CM). Um vetor direcionado para o centro de massa é uma soma linear de vetores direcionados a partir de todos os pontos de massa de um corpo sólido dividido pela massa de todo o corpo, M:

$$

$$r ^ {CM} = {\ sum_ {i} {m ^ i r ^ i} \ sobre {M}}$$

Equação 8

Usando a definição do centro de massa, podemos simplificar a Equação 7 multiplicando os dois lados da Equação 8 por M, diferenciando-os e substituindo o resultado na Equação 7:

$$

$${{d (Mr ^ {CM})} \ over {dt}} = {\ sum_ {i} {} {{d (m ^ ir ^ i) \ over dt}}} = {\ sum_ {i} {} {m ^ iv ^ i}} = p ^ T$$

Equação 9

O lado direito da Equação 9 é o momento total, conforme definido na Equação 7. Agora, vamos olhar para o lado esquerdo da equação: esta é a velocidade no centro da massa vezes a massa do corpo inteiro. Mova o lado direito para a esquerda e obtenha:

$$

$$p ^ T = {{d (Mr ^ {CM})} \ over {dt}} = Mv ^ {CM}$$

Equação 10

Segue-se da Equação 10 que o momento linear é igual à massa total vezes a velocidade direcionada a partir do centro de massa, portanto, não é necessário somar na Equação 7 para encontrar o momento se conhecermos a massa do corpo e a direção do vetor de velocidade do centro de massa. Além disso, todos os resultados finais dos cálculos estão encontrando as integrais para todo o corpo, mas o centro de massa existe e simplifica bastante a determinação do momento total da Equação 10, portanto não podemos nos preocupar - para encontrar o momento linear, podemos considerar o corpo como um ponto material com velocidade e massa.

Por analogia, a força total é uma derivada do momento total; portanto, o conceito de centro de massa pode ser usado para simplificar a equação da força:

$$

$$F ^ T = p ^ T = Mv '^ {CM} = Ma ^ {CM}$$

Equação 11

Em resumo, segue-se da Equação 11 que podemos considerar todas as forças que interagem com um sólido, como se seu vetor soma tivesse um efeito no ponto do centro de massa, que contém a massa de todo o corpo. Dividimos a força (leia a gravidade) por M para encontrar a aceleração do centro de massa e depois integramos a aceleração no tempo para obter a velocidade e a coordenada do corpo. Porque ignoramos os efeitos da rotação até o próximo artigo, já temos todas as equações necessárias para descrever a dinâmica de um corpo rígido. Observe que a Equação 11 não contém informações sobre para onde as forças aplicadas ao corpo são direcionadas. Isso aparecerá quando lidamos com o momento linear e o centro de massa, e apenas aplicamos forças ao CM para encontrar a aceleração do centro de massa. Quando calcularmos a rotação do corpo sob a influência dessas forças no próximo artigo, veremos como a coordenada da aplicação da força é usada.

Ode à Alegria

Nesse estágio, podemos considerar outro exemplo de integração analítica, usando a Equação 11 para encontrar a aceleração do centro de massa em vez de um valor escolhido arbitrariamente = 5. No entanto, enfrentamos um problema sério, pois a integração analítica geralmente não tem um valor aplicado, porque como é muito complicado, focaremos na chamada integração numérica de equações diferenciais ordinárias (ODEs). Uau, agora isso parece matemática de verdade! Depois de aprender isso, será a hora de aumentar a fasquia. Felizmente, a integração numérica dos ODEs não é tão difícil quanto parece à primeira vista! Para entender o que isso significa, passamos de palavras para ações!

Portanto, uma equação diferencial é uma equação que contém derivadas de quantidades dependentes, além da própria função, variáveis ​​e parâmetros independentes. Isso é detalhado, mas aqui está um exemplo para uma força variável no tempo em um mundo unidimensional: F = 2t, F é uma quantidade dependente e t é independente. O valor de F é determinado apenas por F. Deixe a equação da força depender apenas da velocidade do nosso corpo.A força da resistência do ar aumenta com o aumento da velocidade da aeronave. Voltemos ao exemplo no mundo unidimensional, e se F = -v significa que a força de atrito diminui a velocidade do corpo em proporção à velocidade? Temos um problema, porque resolvemos a equação da seguinte forma: F = ma = -v e, dividindo por m, obtemos (lembre-se de que a aceleração é uma derivada da velocidade):

$$

$$a = {{dv}\over {dt}} = {-v\over m}$$

Equação 12

Essa equação diferencial (a equação de velocidade contém a derivada de velocidade na Equação 12) é chamada de equação diferencial ordinária, porque contém apenas derivadas ordinárias de quantidades dependentes (em oposição a derivadas parciais, que compõem equações diferenciais parciais [PDEs]), sobre as quais não somos nós conversaremos).

Agora vamos para a próxima parte da nossa frase: integração. Como integramos anteriormente dv / dt para encontrar v nas condições desta equação?

Isso parecerá inacreditável, mas quase todas as equações da física são diferenciais; portanto, as EDOs foram bem estudadas. Equações diferenciais podem muitas vezes ser encontradas na física, porque muitas vezes a taxa de mudança de uma quantidade quantitativa depende da própria quantidade. Por exemplo, já observamos que a frenagem (a magnitude de uma mudança na velocidade), incluindo a velocidade da resistência do ar, depende da velocidade. Outros exemplos da física: resfriamento (a taxa de perda de calor depende da temperatura atual) e decaimento radioativo (taxa de decaimento depende da quantidade de material radioativo presente).

A palavra final em nossa frase - numérica - é a nossa salvação. Digo isso porque a teoria da integração analítica de equações diferenciais, mesmo as mais simples, é enorme e bastante confusa. Embora, ironicamente, a integração de EDOs usando métodos numéricos de computador seja realmente relativamente fácil de entender. A seguir, descreverei um integrador numérico simples baseado no método de Euler e o refinarei no próximo artigo.

Quase todos os integradores numéricos, mas nenhum outro tão explícito quanto o método de Euler, são simplesmente baseados na antiga definição de computação através da primeira derivada da inclinação: dy / dx determina a inclinação de y, dependendo de x. Por exemplo, se tivermos a equação linear y = 5x, dy / dx = 5 significa que a inclinação é uma constante igual a 5 para qualquer x e, como você pode assumir, esta é uma linha reta. Um exemplo um pouco mais difícil é a parábola y = x2. Nesse caso, dy / dx = 2x, e essa é uma função para determinar a nova inclinação para cada coordenada x. Descrevi y = x2 na Figura 2: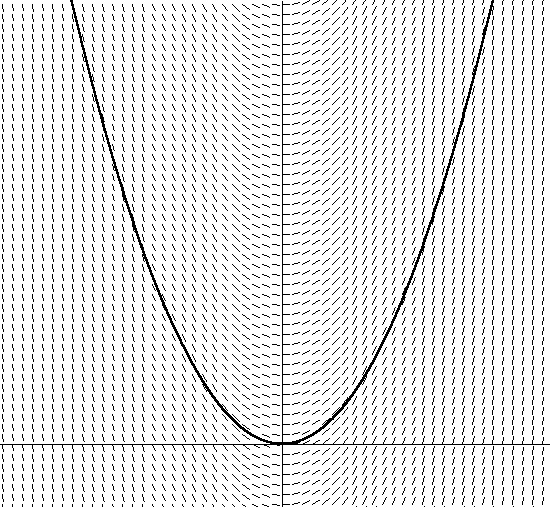



Figura 2. y = x2

Além disso, também tracei a direção do vetor oblíquo, resolvendo a equação dy / dx = 2x + C para todo x. Preste atenção ao fato de que o ângulo do vetor inclinado é igual à tangente ao ângulo tangente nesse ponto. Observe também que existem muitas parábolas diferentes que satisfazem o ângulo do conjunto de tangentes, diferindo apenas em uma mudança ao longo do eixo y. Cada uma dessas parábolas é obtida usando diferentes constantes de integração, que estão contidas na equação dy / dx = 2x + C. A parábola que imaginei tem uma constante de integração de 0. Se eu escolher outra constante, por exemplo, 1, obtenho a equação y = 2x + 1. Isso significa que há uma parábola semelhante com um deslocamento de 1 unidade no eixo y.

Agora pense no fato de que, se você não conhece o campo de vetores na Figura 2 definido por uma parábola, sente-se em uma poça. Portanto, se você deseja resolver a equação tangente, basta seguir a direção do vetor em cada ponto, alterando a direção de acordo com a mudança na direção do campo vetorial. Você ficará surpreso que, após algum tempo, verá que está se movendo ao longo de uma trajetória parabólica (ou ao longo de uma seção da parábola), dependendo de onde você começou. Sem perceber, você integrou a equação do campo vetorial. Você encontrou uma parábola específica (dependendo de onde você começou ou das condições iniciais), usando apenas a equação derivada (calculando dy / dx à medida que você se move no campo vetorial).

Fazer o mesmo para uma equação diferencial real também é simples. Para uma equação diferencial do tipo dy / dx = f (x, y), encontrar a derivada dy / dx como tangente a f (x, y) descreve o ângulo de inclinação da tangente para cada coordenada no gráfico x, y. Se você estiver plotando um campo vetorial dado por dy / dx = f (x, y), poderá fazer isso por analogia com uma parábola, localizando a derivada em cada ponto e seguindo nessa direção. A Figura 2 mostra um campo vetorial para a Equação 12, nossa equação para resistência do ar, com velocidade ao longo do eixo vertical e tempo ao longo da horizontal (eu escolhi arbitrariamente m = 1 para este gráfico).



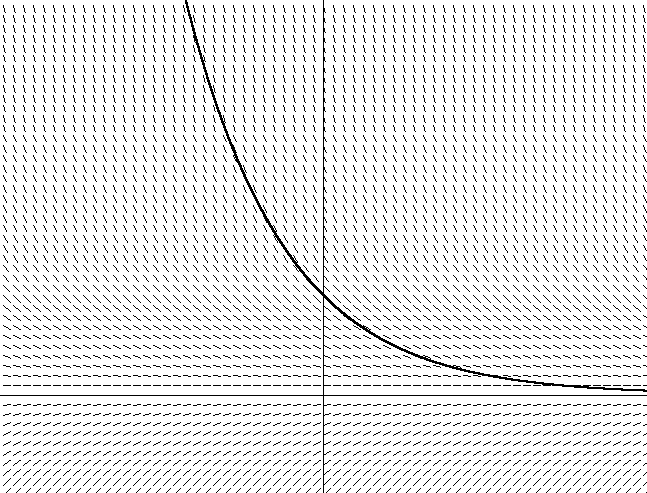Figura 3. dv / dt = -v / m

Também mostra uma das muitas curvas possíveis. Você pode notar que, se você escolher a posição inicial no gráfico (que depende da velocidade inicial na equação), com o tempo, a velocidade tenderá a zero, porque a força de atrito diminui o corpo. Você também pode ver como a diminuição da velocidade depende do valor atual da velocidade - quanto mais rápido você se move, mais rápido ele diminui. Isso se torna aparente quando o mesmo se segue da Equação 12.

A integração numérica é semelhante ao que fizemos no gráfico. O algoritmo de Euler para integração numérica simplesmente segue o campo vetorial de acordo com a posição inicial, encontrando a derivada da equação (-v / m para nosso exemplo com a força de atrito) para determinar a inclinação no ponto atual e, em seguida, simplesmente avançando passo a passo no tempo, dependendo de valor inalterado de h, ao longo da inclinação. Em seguida, uma nova posição é calculada para determinar a nova inclinação após um certo intervalo de tempo:

$$

$$y_{n+1} ≈ y_{ n } + {h(dy_{ n })\over dx}$$

Ou, mais precisamente, para nossa equação de resistência do ar:

$$

$$v_{ n+1 } ≈v_{ n }+{h( -v_{n})\over m}$$

Obviamente, o método Euler dá um pequeno erro a cada etapa do tempo, uma vez que o vetor de velocidade real (e, portanto, a curva da solução) se curva com um desvio em cada ponto, e o algoritmo de Euler se desvia ligeiramente do ângulo de inclinação. Mas se o intervalo de tempo, h são quantidades bastante pequenas, o erro tende a zero. Discutiremos isso com mais detalhes no futuro.

É tudo o que você precisa saber sobre integração numérica usando o método Euler. Você pode perguntar como vamos integrar a velocidade para obter a coordenada. Simplesmente usamos o método Euler novamente para integrar dr / dt = v, assim como integramos dv / dt = a, por analogia. Temos duas equações diferenciais conectadas (mais uma de nossa vitória):

$$

$$v_{n+1} ≈ v_n+hv'=v_n+{h F_n\over M }$$

$$

$$r_{ n+1 } = r_n + hr_n'= r_n+hv_n$$

Isso nos dá um algoritmo alternativo para calcular a coordenada após a ação de qualquer força aplicada arbitrariamente em nosso objeto (que pode depender da velocidade, como vimos, ou do tempo, ou mesmo da posição do nosso corpo e de outros corpos, ou de uma só vez!). Para o método de Euler, não importa a aparência da força aplicada, pois você pode calculá-la a qualquer momento. Euler está interessado na magnitude do efeito da força na massa, como inclinado, e é isso.
Eu fiquei sem espaço, então não tenho como fornecer links. Da próxima vez, aconselharei vários livros maravilhosos e descobriremos como calcular a rotação de sólidos.

E embora seu corpo não seja tão sólido quanto gostaríamos, Chris Hecker tem uma personalidade dinâmica. Se você aplicar força, ele responderá pelo e-mail checker@bix.com.

Notas do tradutor: um trocadilho é apresentado aqui, o tópico do artigo e seu conteúdo são exibidos.

PS O autor da tradução agradece especialmente aos usuários do berez e do MarazmDed pela edição da tradução. Obrigada