Colado por dezenas de sensores, o "objeto de pesquisa" durante testes dinâmicos em larga escala (por exemplo, ao estudar a atividade vibracional do veículo) fornece facilmente uma grande quantidade de dados, mas geralmente não é muito claro o que fazer com ele. O mesmo ocorre com a modelagem de simulação de processos dinâmicos de sistemas com um grande número de graus de liberdade.
Isso pode não estar completamente claro para quem não encontra um problema regularmente, mas observar a animação correspondente de um processo estocástico no tempo e no espaço geralmente é quase inútil. Onde ele quebra ou porque treme assim - geralmente "não visível". O que eles criaram além da animação, vou contar abaixo, mas eu recomendo.
Por meio de um procedimento elementar, também é possível obter as “formas” espaciais das próprias oscilações; além disso, são elas que realmente aparecem sob as condições de carregamento fornecidas e a intensidade de sua manifestação (dispersão; se desejado, os próprios processos).
Fonte
multicanal
o processo
 | Decomposição
|
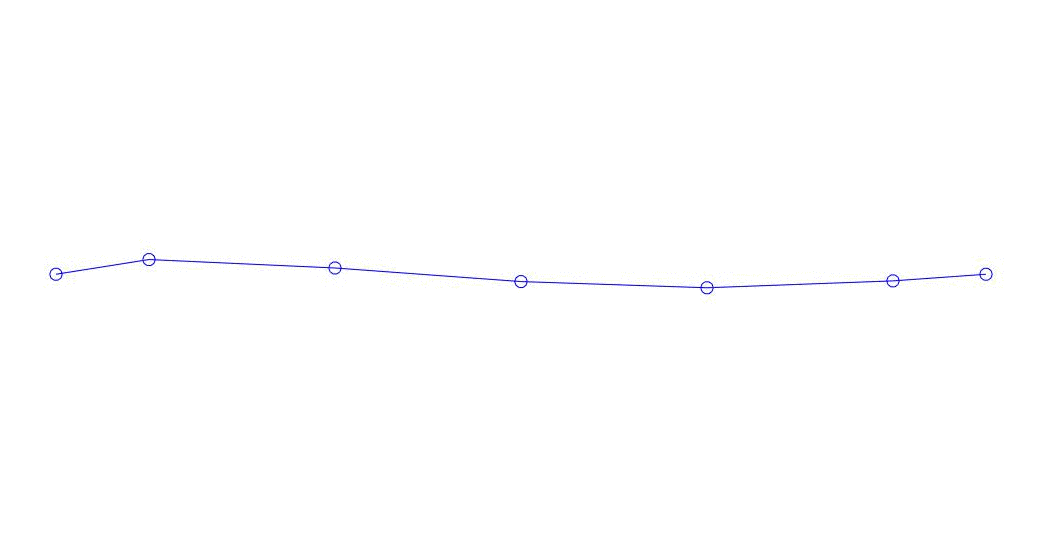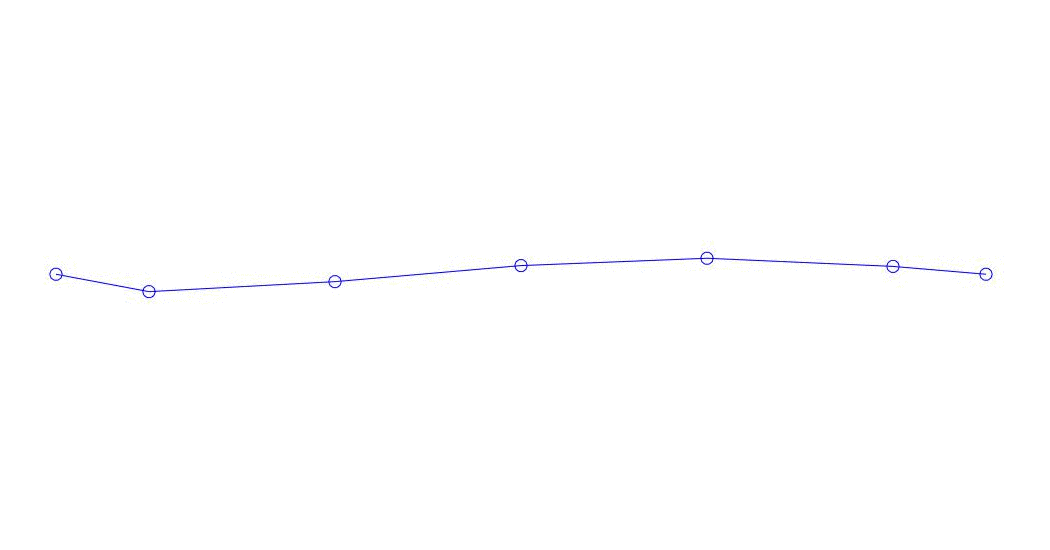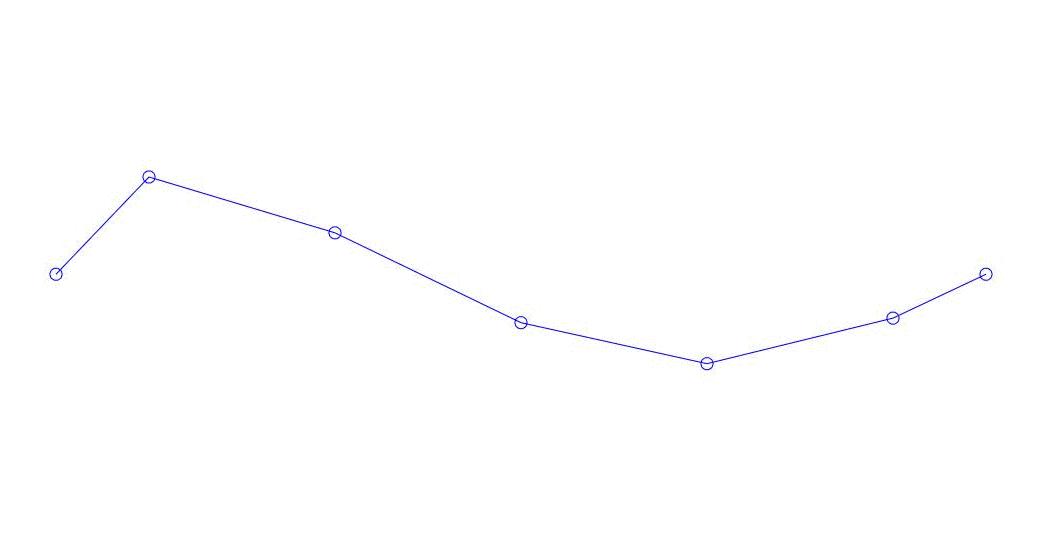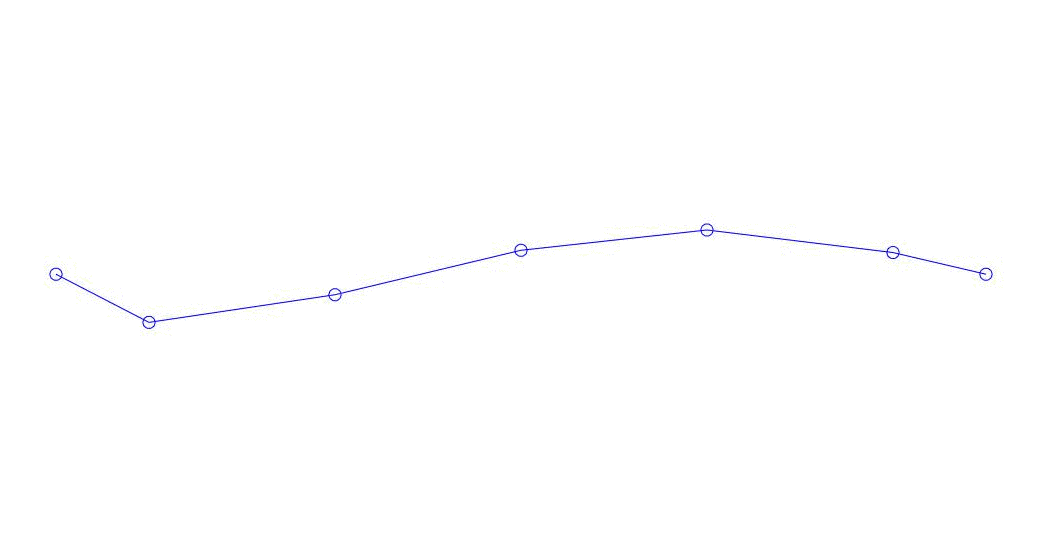
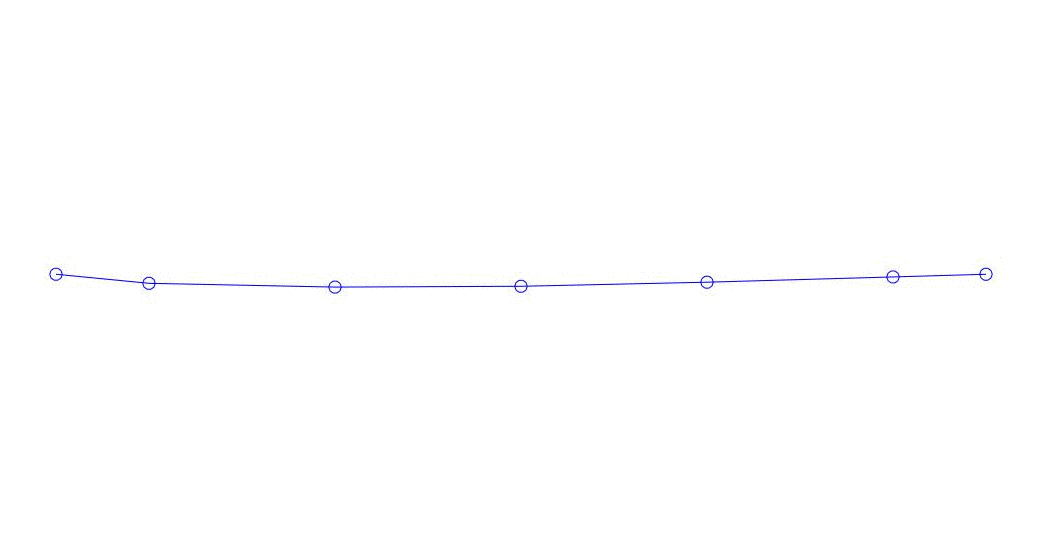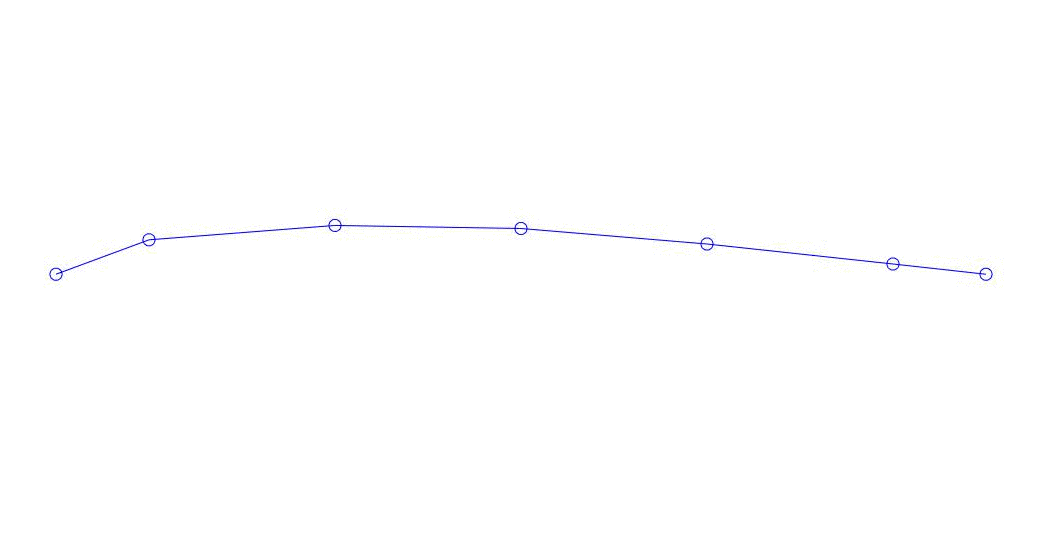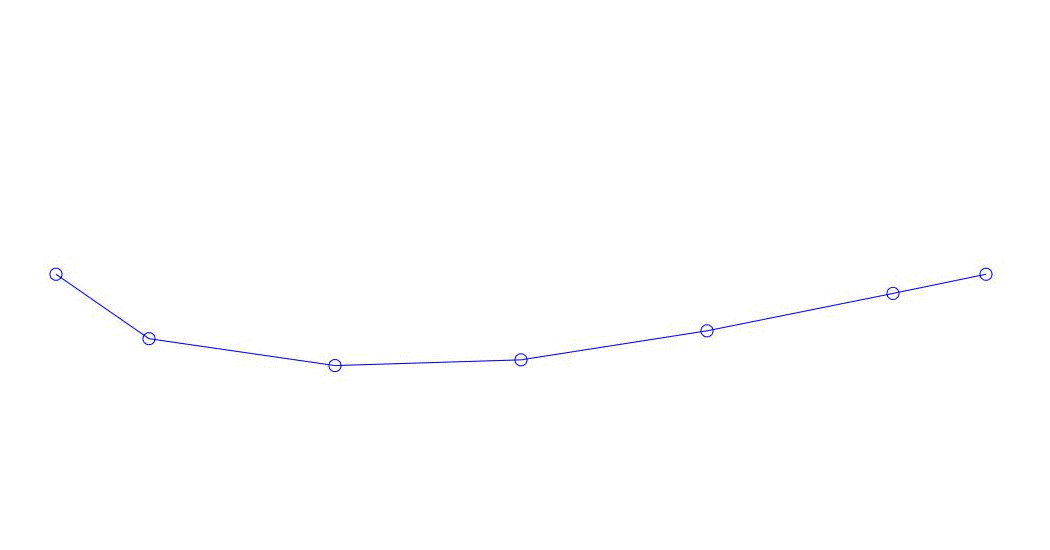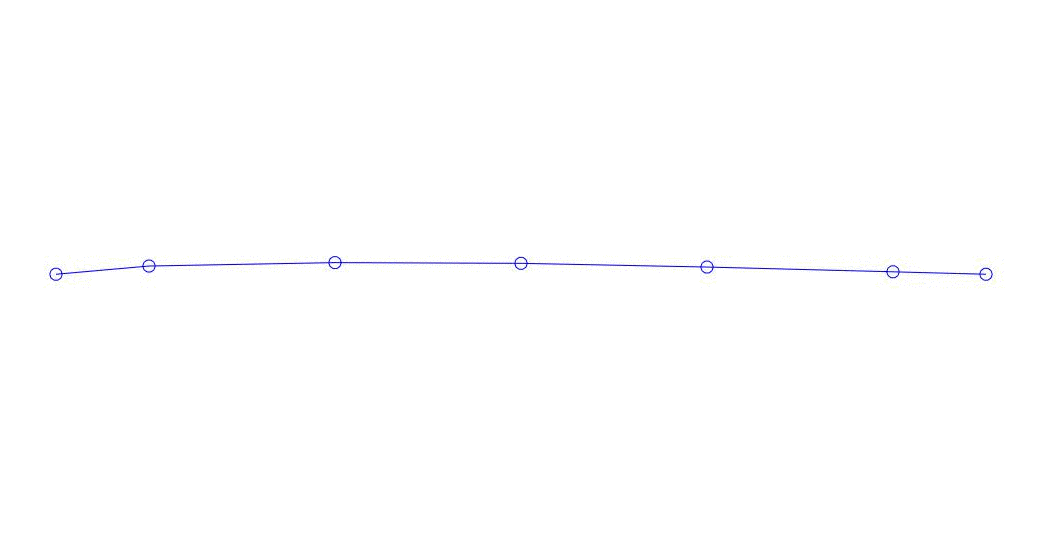
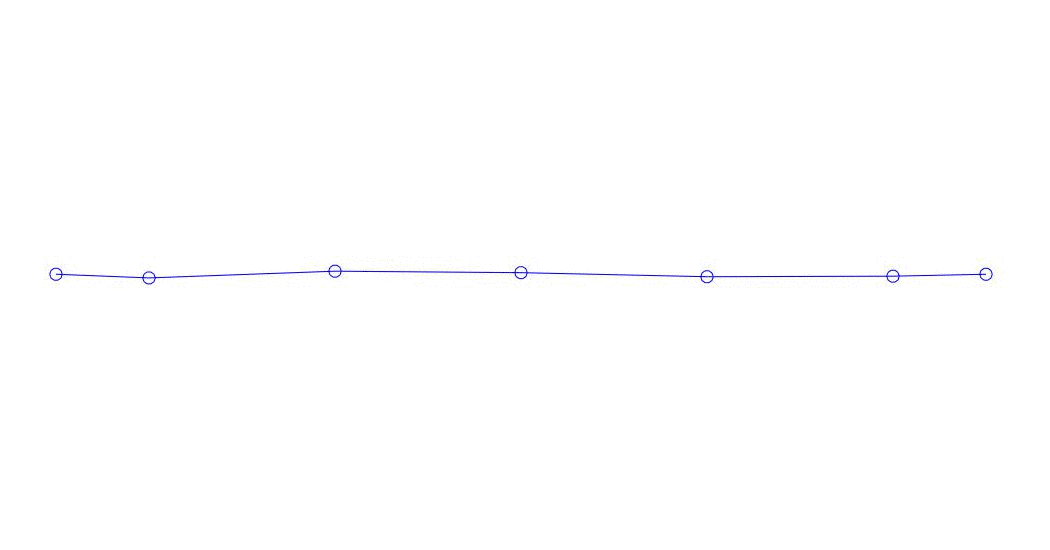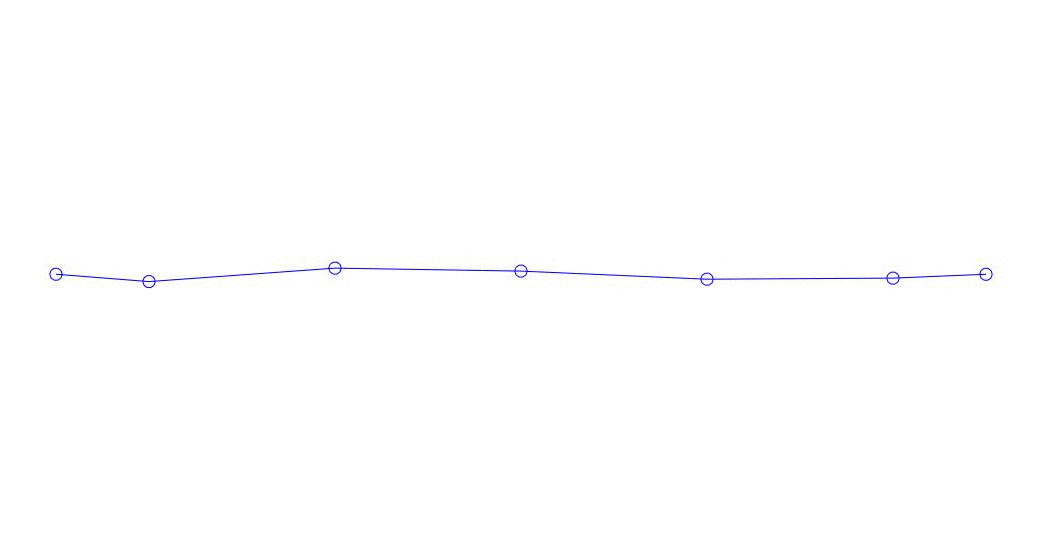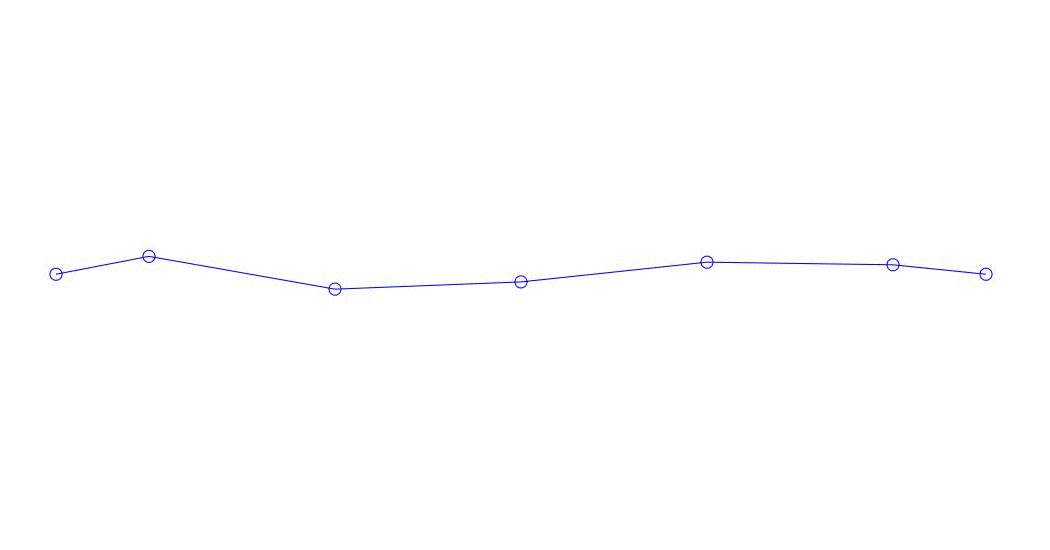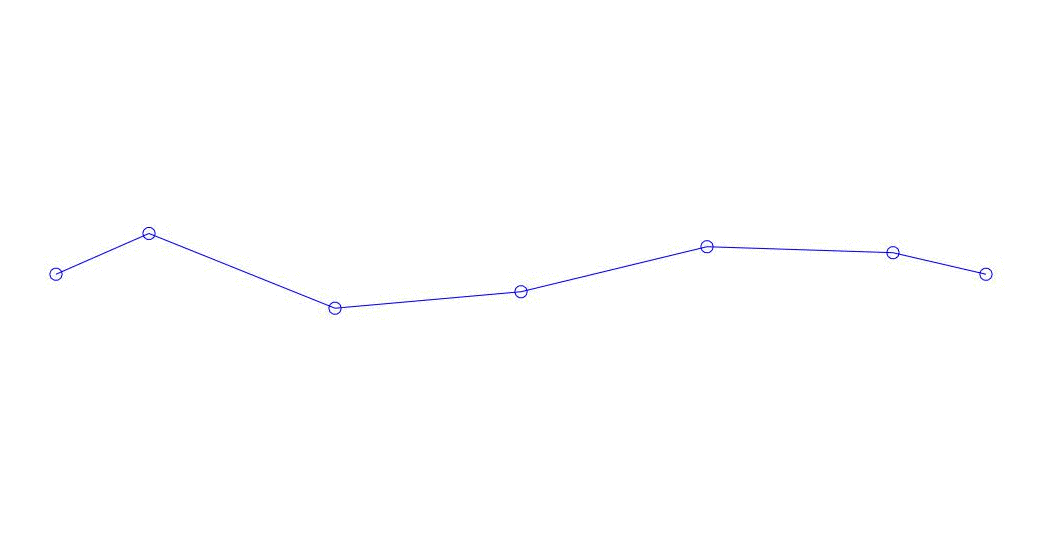
Fig. 1 Decomposição de uma resposta multicanal em pseudo-formas. “Corda em um meio viscoso” (veja a figura 2)
Além da animação, são conhecidos estudos "em pares" (espectros mútuos, etc.) que, é claro, não dão uma imagem geral.
Tais métodos são bastante óbvios - ao “cortar” bandas muito estreitas do espectro correspondente a picos ressonantes nos espectrogramas, os métodos de espectrograma (novamente “em pares”) produzem quase formas de vibrações quase harmônicas (altamente correlacionadas).
Além da óbvia complexidade técnica, a desvantagem de tais métodos é que você geralmente precisa "escolher com êxito" um canal de "referência", o que nem sempre é possível. Como resultado, erros muito grandes ocorrem nas fases mútuas dos processos. Além disso, a forma espacial distinta das oscilações e sem esses erros, devido às propriedades de um sistema linear, pode se tornar “complexa” (não-fase), cujo valor para análises subjetivas subsequentes geralmente reduz (significativamente).
Sabe-se um estudo de 4 canais de vibrações torcionais (o sistema transportador de um ônibus médio), que é alocado em um processo usando a forma vibracional espacial determinada pela inspiração do pesquisador - foram adicionadas as leituras de dois sensores localizados na diagonal nos cantos do corpo (tiradas de "+"), de foram subtraídos (tirados de “-”) o testemunho de dois outros localizados axissimetricamente.
Mesmo com um pequeno número de sensores, essa abordagem pode não ser totalmente boa. Por exemplo, a estrutura de um caminhão é geralmente muito mais maleável na parte do sub-motor (frente), respectivamente, em uma forma de torção, talvez deva ser assumida de uma forma mais complexa (provavelmente com alguns coeficientes "crescentes" para os sensores dianteiros - e, ao mesmo tempo, a questão de fundamentar o aceite) modelos). Com um número maior de canais de vigilância, tudo isso é muito complicado e pouco justificado.
A separação explícita (em processos separados) de várias formas de vibrações (modos), previamente determinadas a partir de outro experimento ou modelagem, já foi proposta por mim (provavelmente não apenas por mim) e foi chamada pelo meu chefe, então "o método de decomposição modal". Deveria analisar os resultados dos testes de campo dessa maneira e determinar os vetores de suas próprias formas por testes de bancada (ou modelagem por elementos finitos).
Na verdade, eles fizeram isso, mas, ao mesmo tempo, isso aconteceu.
É claro que os “experimentadores de bancada”, ao contrário dos “polígonos”, estão disponíveis para observação síncrona, um verdadeiro processo perturbador. Isso lhes deu uma grande vantagem - eles poderiam determinar as verdadeiras funções de transferência e usar o hardware e o software disponíveis para determinar experimentalmente suas próprias formas e frequências de vibrações estruturais (com base na adaptação, “cortando” as faixas de frequência “a olho” e indicando ao sistema quantas formas existem encontrar; também, mais arte do que ciência, mas ainda).
No entanto. Evitaram claramente explorar um objeto, como uma montagem de carro, preferindo estruturas individuais, corpos de suporte etc. - objetos com amortecimento muito baixo. Trata-se de testes de bancada modais - a determinação de frequências e formas naturais. Não é sobre simulação. Modos intrínsecos plausíveis de vibração em objetos um pouco mais fortemente amortecidos podem ser obtidos experimentalmente experimentalmente, mas significativamente mais difíceis.
Informações muito valiosas revelaram-se sobre essas "preferências". Se for muito, muito curta - apenas as conclusões que foram subseqüentemente alcançadas: dificilmente vale a pena tentar decompor a resposta precisamente nas verdadeiras formas apropriadas da construção, apesar da "beleza" da idéia.
Se estiver "nos seus dedos", é provável que o motivo seja de alta probabilidade - dependendo da perturbação externa, os "modos próprios de oscilações" (mais precisamente, processos estacionários "modais" correspondentes aos modos próprios de oscilações) provavelmente serão assim ou de outro modo, eles estão correlacionados entre si, na verdade formando outras formas espaciais de vibrações, em um grau ou outro diferente do seu, e isso naturalmente se manifesta em uma forte dependência do amortecimento da estrutura.
Como uma breve explicação "pelo contrário" - dois harmônicos "não amortecidos" diferentes não são correlacionados, é claro, sempre nada. (Explicação. O efeito acima mencionado de "misturar formas próprias" é observado tanto na ausência de "não linearidades significativas" quanto fora de "formas complexas" com amortecimento "desproporcional" em sistemas lineares.)
Com base no exposto, propõe-se apresentar a resposta do sistema como a soma de vários processos independentes de correlação, como certas formas de vibração (flexão, torção, etc.). Essa análise é muito simples, como regra, fornece resultados muito valiosos. As formas obtidas podem ser semelhantes aos modos próprios de oscilação do sistema, ou não, mas sempre refletem o comportamento do sistema precisamente sob condições de influência externa real. além disso, refletem o mais simples e informativo possível, e sua sequência, classificada por suas variações, é uma série aproximada.
Para obter a decomposição de seu interesse, consideramos (1),
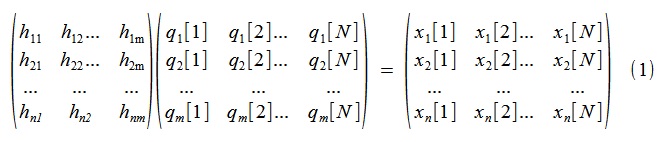
ou, de forma compacta, (2),
onde
x é a resposta física do canal n obtida diretamente do sistema com a duração de N amostras,
q é o processo "modal" real do canal m com canais mutuamente não correlacionados, H é a matriz de colunas que descreve os modos de vibração em fase ("real") desejados.
De um modo geral, m <n é subseqüentemente esperado (o número de formas é menor que o número de canais de resposta física), mas, inicialmente, assumimos que m = n, se H e
q são da classificação n, (2) em qualquer caso, é satisfeito sem um resíduo, obviamente chegamos a
| H · Rqq [0] · H T = Rxx [0] (3) |
ou com mais detalhes
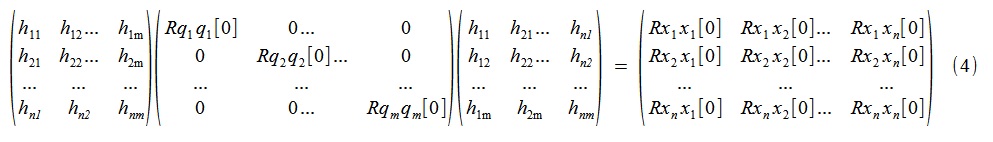
Ou seja, a busca pelos modos de vibração “pseudo-apropriados” procurados e os correspondentes processos não correlacionados (com atraso zero)
q se reduz à decomposição espectral (em termos de vetores e números próprios) da matriz simétrica Rxx [0] (composta pelos valores de correlações automáticas e cruzadas dos processos
x para lag Δτ = 0) Seus próprios vetores ortonormais nos dão as formas desejadas, e os valores próprios reais dão as variações dos processos correspondentes (além dos significativos, provavelmente haverá variações de ~ 0, portanto, na prática geralmente m <n). Se desejado, você ainda pode construir os processos em forma de realizações temporárias, encontrar seus espectros, etc.
Para esclarecer o exposto, consideramos um modelo de sistema mecânico linear com cinco graus de liberdade, simulando aproximadamente o comportamento de uma corda em um meio viscoso (Fig. 2),
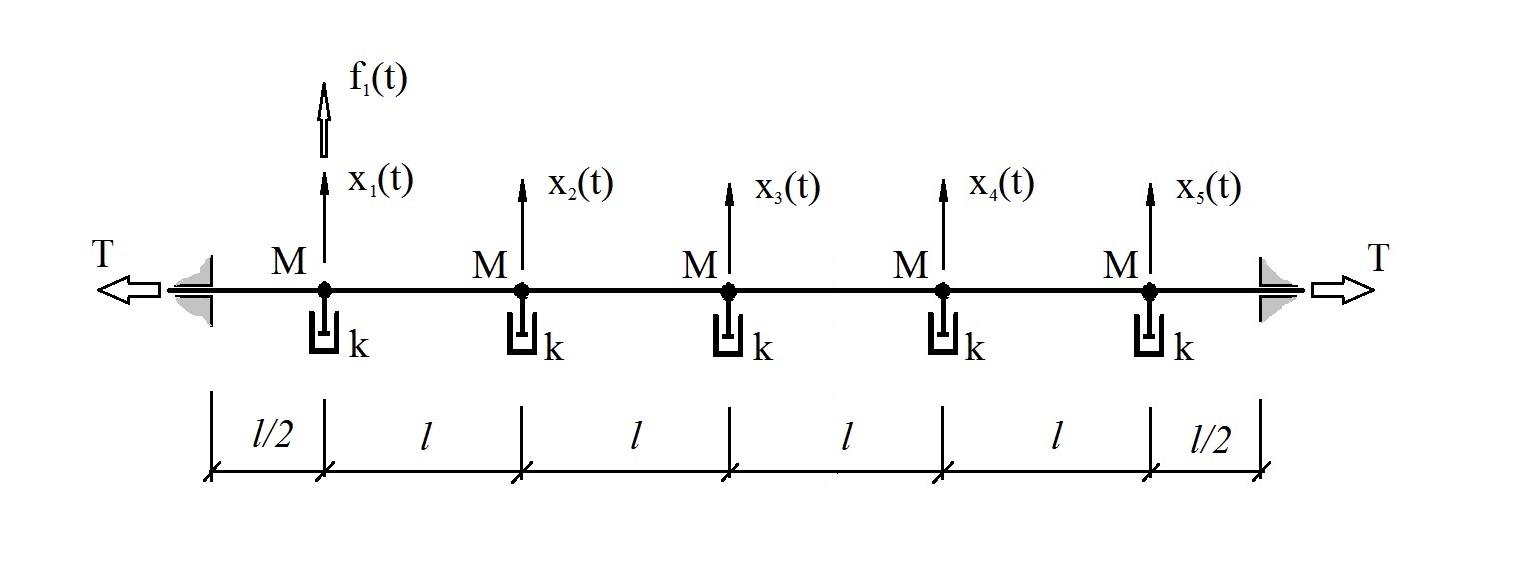Fig. 2 Sistema de teste.oscilando sob a influência de perturbação estocástica f
1 [i] do tipo de ruído rosa (Fig. 3), intervalo de amostragem Δt = 0,01 s, comprimento de implementação 25000 amostras. Sobreposição de 60% dos segmentos.)
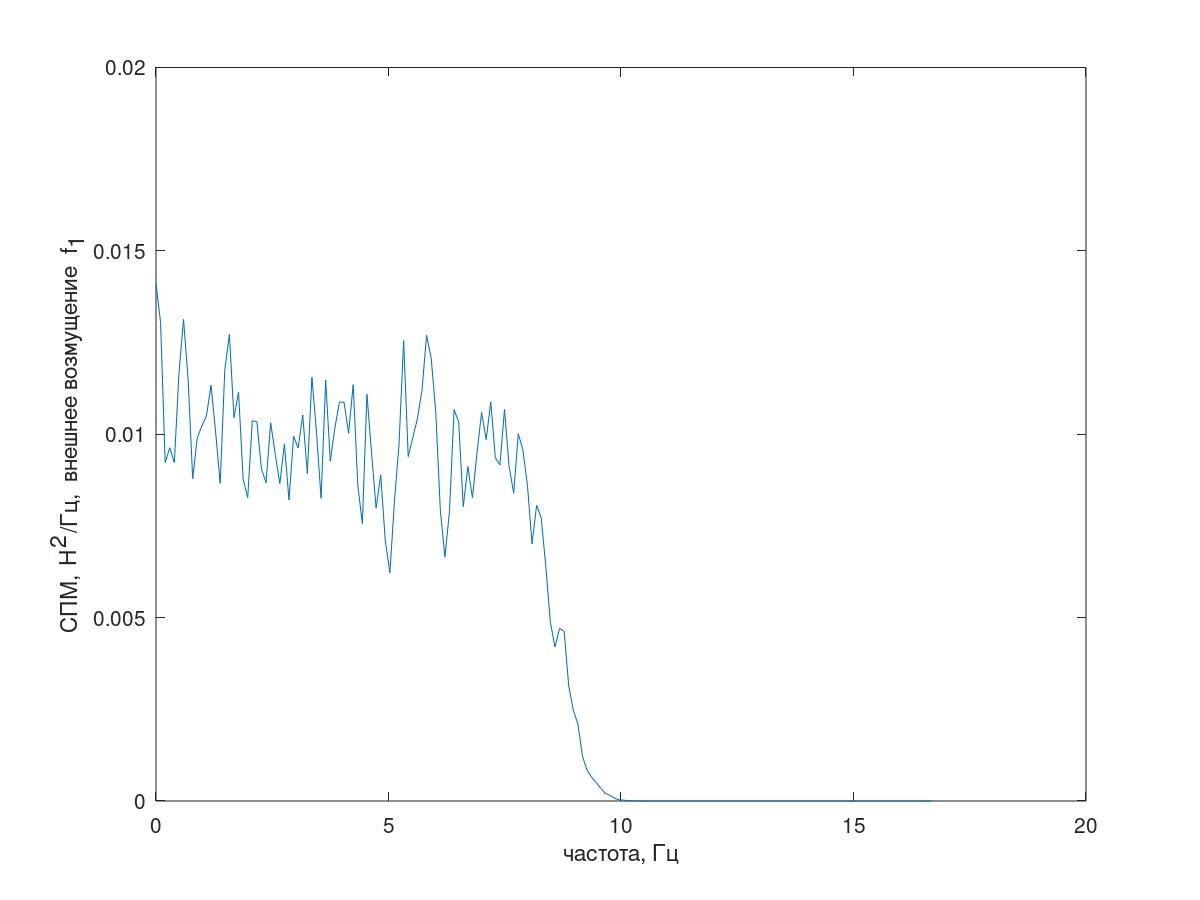Fig. 3 Espectro de perturbação externa.
Um fragmento da implementação temporária da perturbação é mostrado na Fig. 4.
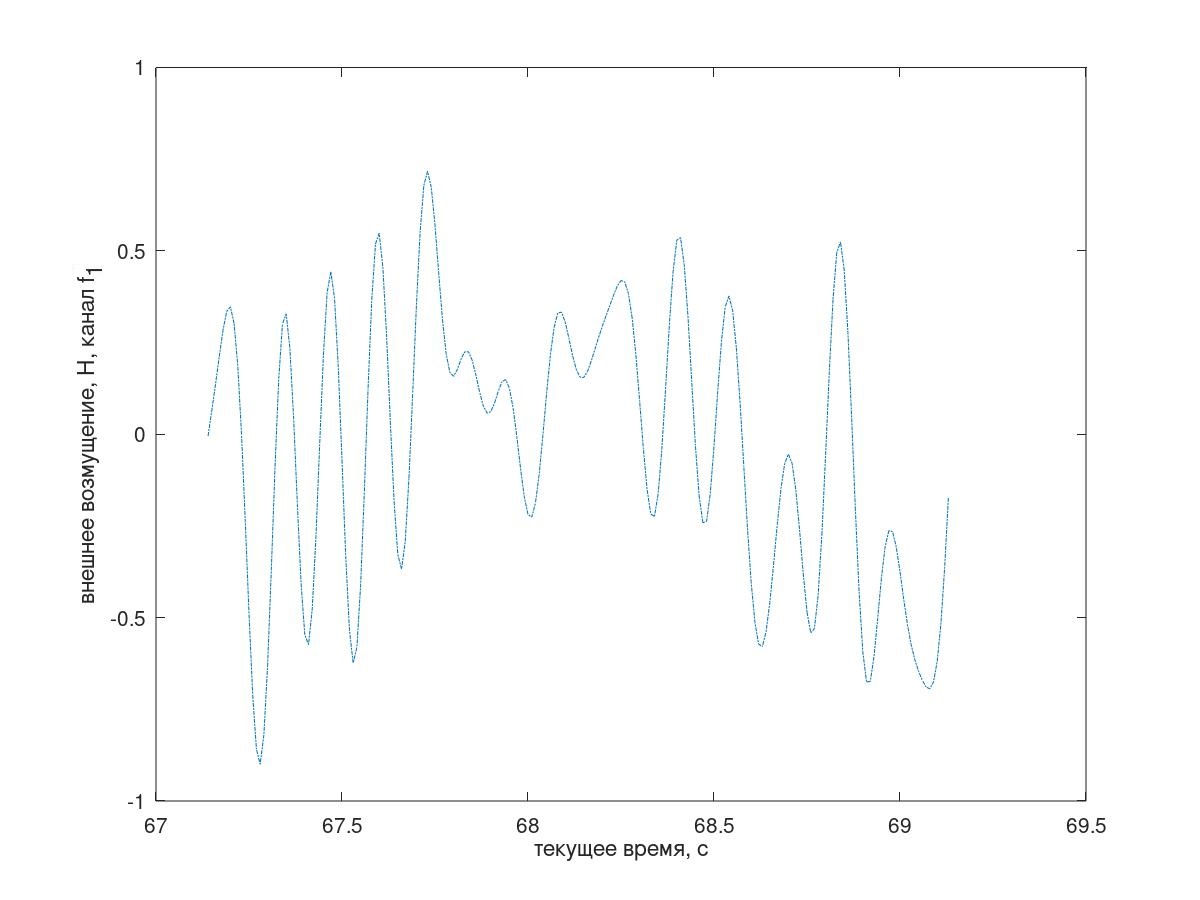
Fig. 4 Um fragmento da implementação temporária da perturbação recebida
Em tempo contínuo, o modelo é um sistema de equações de difusão (6),
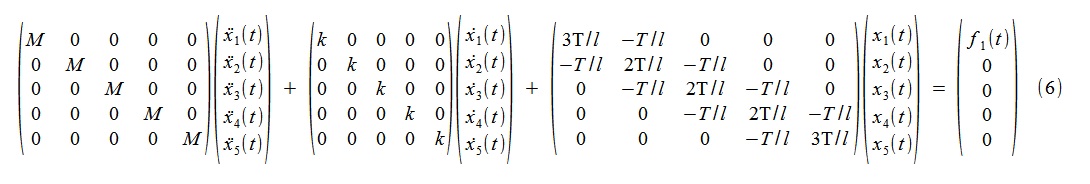
onde M = 1kg, k = 10kg / s, T = 2000N, l = 1m.
As matrizes correspondentes (é claro quais) são numericamente iguais às seguintes:
Uma das respostas de frequência do sistema é mostrada na Fig. 5.
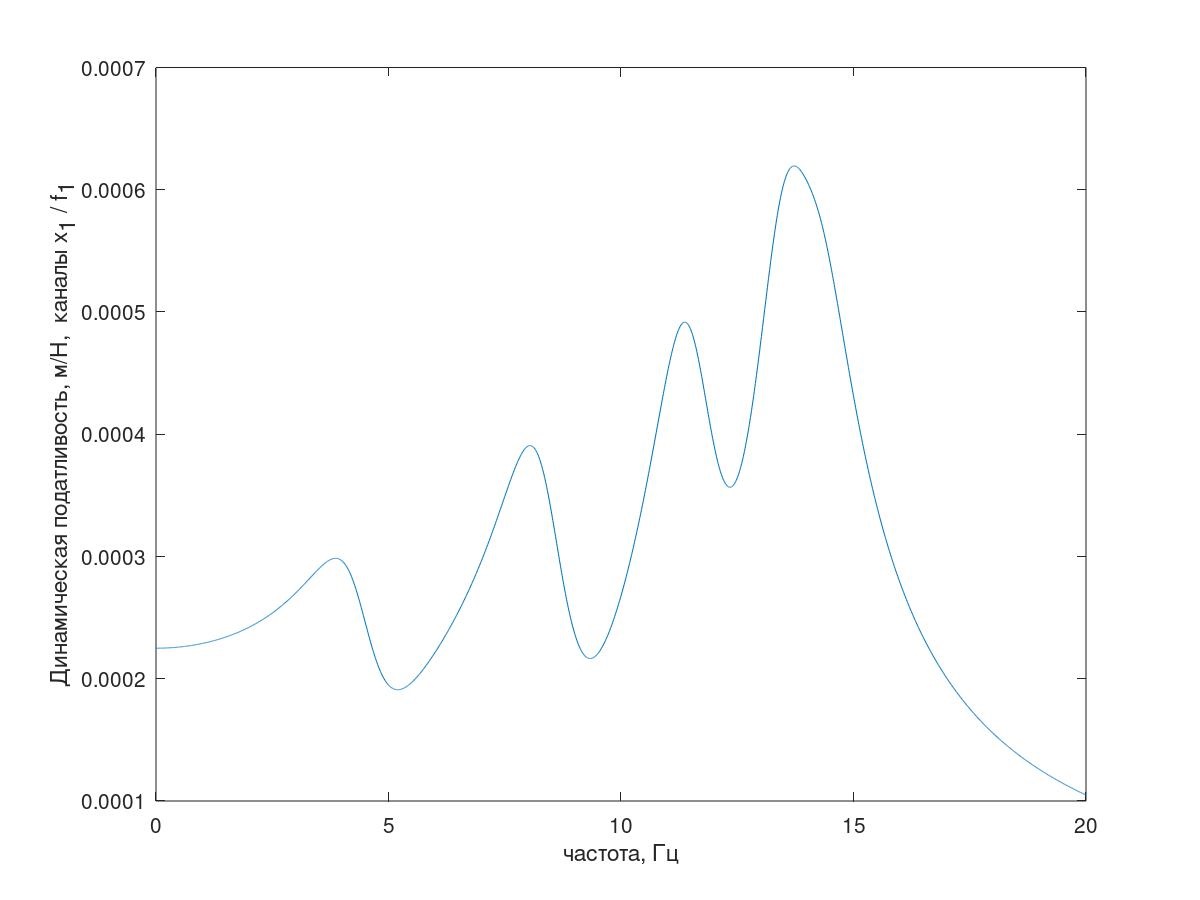Fig. 5. Resposta de frequência do sistema de teste(Explicação - tudo está em ordem com o número de picos ressonantes, como uma explicação dessa resposta de freqüência do sistema com amortecimento condicionalmente reduzido (k = 1 kg / s) é mostrada na Fig. 5)
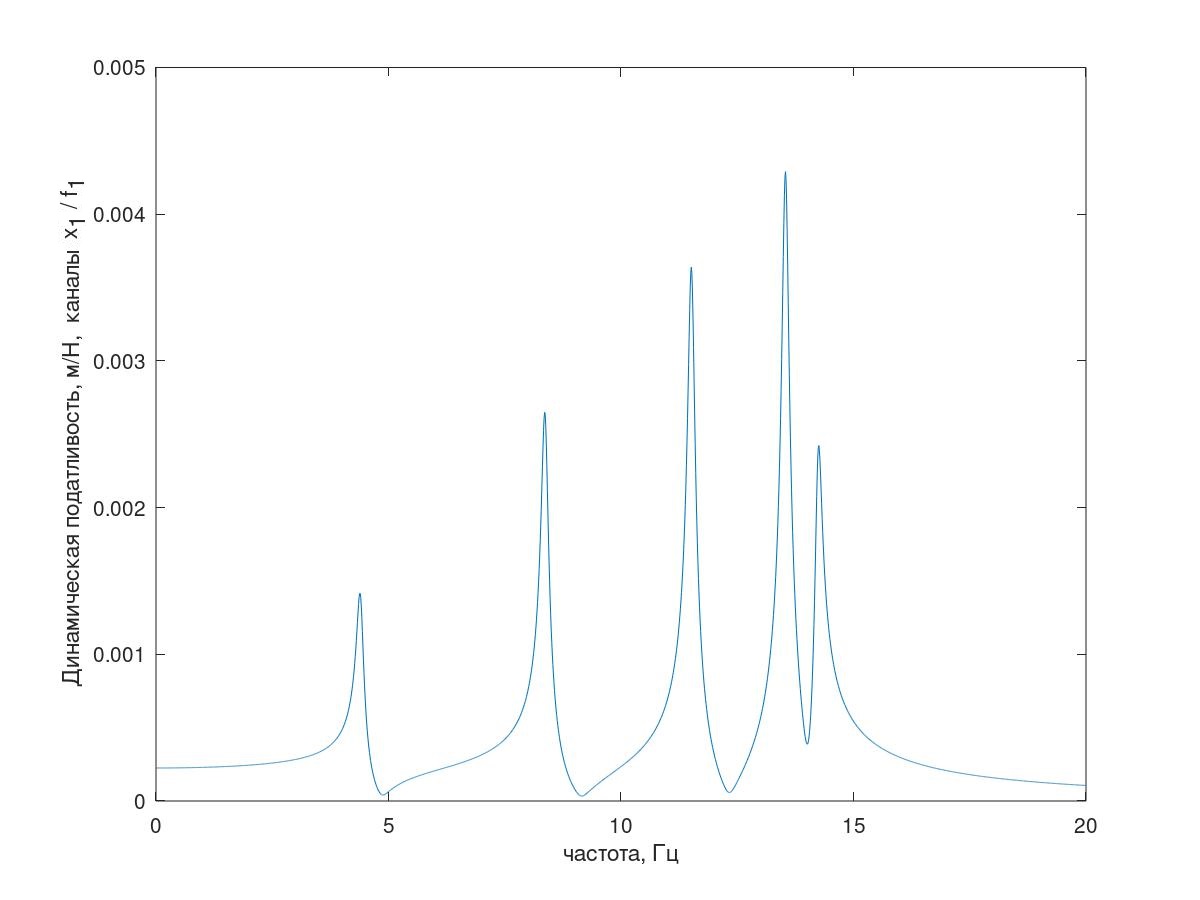Fig. 6 Explicação para cinco ressonâncias.
Para simulação em tempo discreto, é utilizado um modelo de diferença finita (os modelos Raman funcionam bem em pequenos intervalos de amostragem, como
foi mostrado ).
Uma pequena digressão. Algum tempo depois, no âmbito de outro trabalho, foi realizada a modelagem por diferenças finitas deste sistema de teste por outros meios (Xcos \ Simulink). Matematicamente, os modelos são idênticos. Foram obtidas imagens animadas da resposta do sistema a um único impulso no nó 1 e no nó 3. Os resultados são interessantes aqui do ponto de vista da verificação do modelo de diferenças finitas.
(O buffer "imprevisível" dos quadros de software livre estraga um pouco as imagens, principalmente a segunda, mas, em princípio, o resultado é muito bom.)
Mas voltando ao nosso modelo Matlab (GNUOctave). O espectro de resposta resultante é mostrado na Fig. 7.
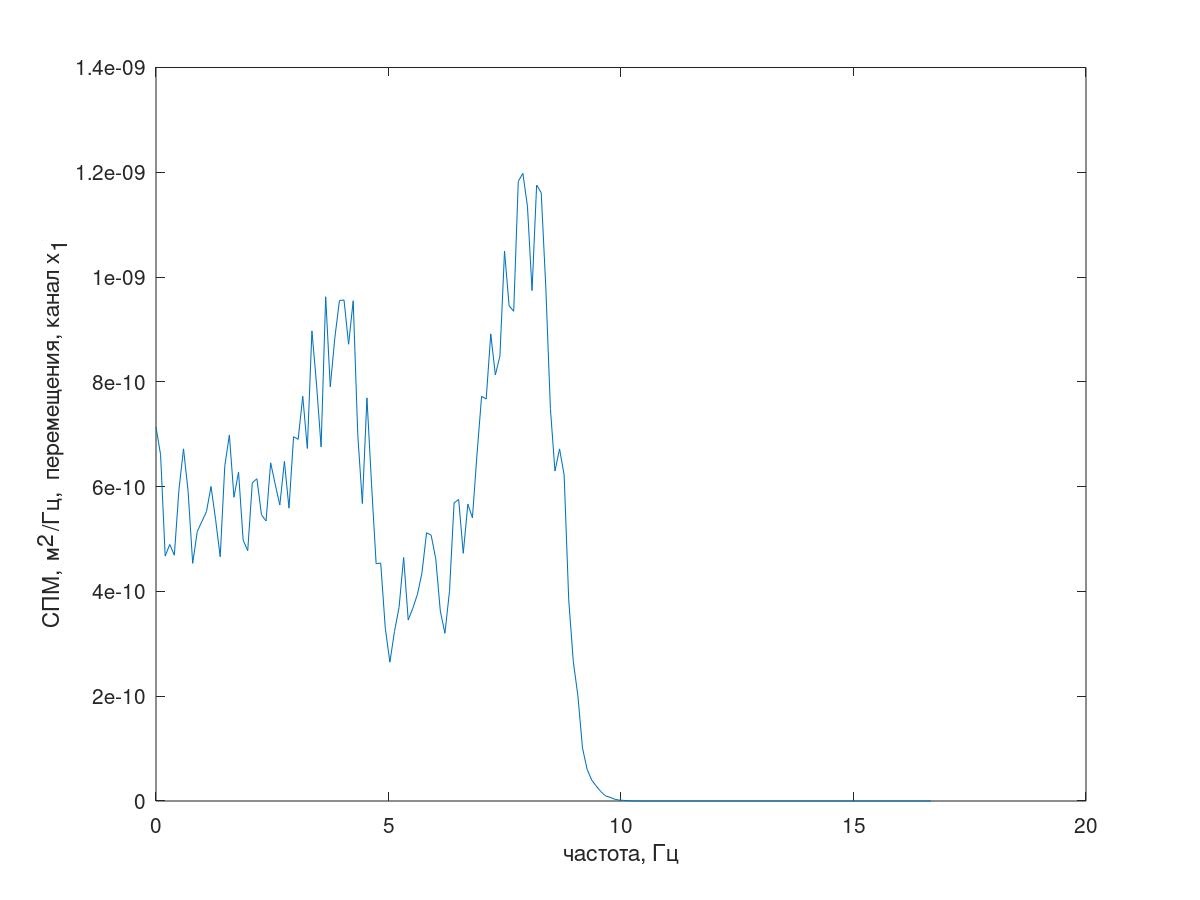Fig. 7 Espectro de resposta (canal x 1 )Além disso, o método de correlação foi usado para encontrar os valores de correlações automáticas e cruzadas dos canais de resposta.
Os resultados da aplicação do método em discussão: foram encontradas variações dos processos pseudo-modais Rqq e formas pseudo-distintas de H:
Os três primeiros processos na decomposição, a animação de todo o processo multicanal e os três primeiros modos de vibração correspondentes em 32 amostras (de 6714 a 6746 amostras, ou seja, de 67,13 s em quantidade) são aparentemente quantitativamente significativas (pelos valores de suas dispersões em Rqq) 67,63 s (hora atual)) é mostrada na Figura 1 no início do artigo. Como você pode ver, essas pseudo-formas têm algumas semelhanças com suas próprias formas de vibração de cordas.
A experiência acumulada indica os seguintes recursos deste método.
- O método é sensível a ruídos estranhos, incluindo alta frequência. Existe o risco de obter resultados "aleatórios" (com um grande erro aleatório) e a aparente irreprodutibilidade dos resultados experimentais. É necessário filtrar cuidadosamente a parte que não funciona (quantitativamente insignificante) da faixa de frequência do sinal multicanal. (Ao mesmo tempo, o trabalho nessa direção foi interrompido devido a relatos de pesquisadores sobre a "ausência" de correlação entre canais - o efeito de ruído forte)
- Os melhores resultados foram obtidos com o número de canais de observação significativamente maior que o número esperado de manifestação de formas vibracionais (o número de picos ressonantes na faixa estudada), ou seja, para m << n.
- Com altos fatores Q, os sistemas de pseudo-formas parecem tender aos verdadeiros modos intrínsecos do sistema. Os resultados obtidos em tais sistemas são mais estáveis em caso de ruído.
- Se o par de autovalores Rxx [0] coincide ou mesmo converge, o par de pseudo-formas correspondentes é determinado, aparentemente, até suas combinações lineares independentes - essas formas não podem ser separadas entre si em determinadas condições experimentais.
- Aparentemente, comparando as formas verdadeiras (encontradas por outros métodos) e as pseudo-formas consideradas, com alguma probabilidade é possível encontrar os pontos de aplicação da perturbação externa (especialmente para perturbação de canal pequeno), se esse problema for relevante.