1. Introdução
A palavra em inglês wavelet (do francês "ondelette") se traduz literalmente como "onda curta (pequena)". Em várias traduções de artigos estrangeiros para o russo, também existem termos: "burst", "função burst", "função de ondas baixas", "wave" etc.
A transformada wavelet (VP) é amplamente usada para análise de sinais. Além disso, ele encontra ótima aplicação no campo da compactação de dados. O VP de um sinal unidimensional é sua representação na forma de uma série generalizada ou integral de Fourier sobre um sistema de funções básicas.
psiab(t)= frac1 sqrta psi left( fract−ba right) (1)
construído a partir da wavelet mãe (fonte)
psi(t) possuir certas propriedades devido a operações de mudança de horário (b) e mudanças na escala temporal (a).
Multiplicador
1/ sqrta garante a independência da norma de funções (1) do número de escala (a). Para os valores fornecidos dos parâmetros aeb, a função
psiab(t) e há uma wavelet gerada pela mãe wavelet
psi(t) .
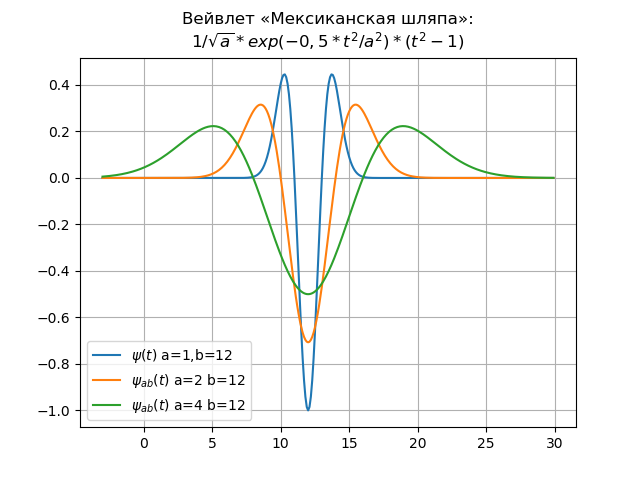
Um exemplo é a wavelet de chapéu mexicana nos domínios de tempo e frequência:
Lista de wavelet para domínio de tempofrom numpy import* import matplotlib.pyplot as plt x= arange(-4,30,0.01) def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f plt.title(" « »:\n$1/\sqrt{a}*exp(-0,5*t^{2}/a^{2})*(t^{2}-1)$") y=[w(1,12,t) for t in x] plt.plot(x,y,label="$\psi(t)$ a=1,b=12") y=[w(2,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=2 b=12") y=[w(4,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=4 b=12") plt.legend(loc='best') plt.grid(True) plt.show()
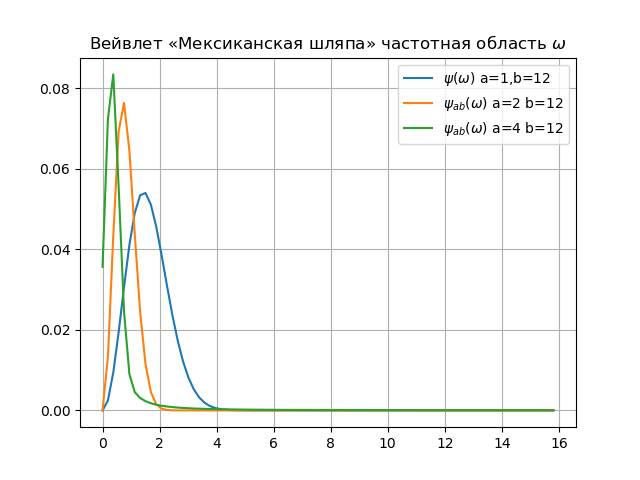
Listagem para o espectro wavelet from numpy import* from pylab import * from scipy import * import os def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f x= arange(-4,30,0.2) def plotSpectrum(y,Fs): n = len(y) k = arange(n) T = n/Fs frq = k/T frq = frq[range(int(n/2))] Y = fft(y)/n Y = Y[range(int(n/2))] return Y,frq xlabel('f (Hz)') ylabel('|Y(f)|') Fs=1024.0 y=[w(1,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi(\omega)$ a=1,b=12") y=[w(2,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=2 b=12") y=[w(4,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=4 b=12") plt.title(" « » $\omega$") legend(loc='best') grid(True) show()
 Conclusão:
Conclusão:1. Entre o conceito de harmônicas de Fourier e a escala da wavelet, existe realmente um relacionamento. A principal coisa nesse relacionamento é a proporção inversa da frequência e escala naturais. Além disso, reduzindo a escala, aumentamos a largura de banda do espectro de wavelets.
2. Alterando a escala (aumentar a leva a um estreitamento do espectro de Fourier de
psiab(t) ), as wavelets são capazes de detectar a diferença de características em diferentes escalas (frequências) e, devido à mudança, analisar as propriedades do sinal em diferentes pontos em todo o intervalo estudado. Portanto, ao analisar sinais não estacionários, devido à localidade das wavelets, obtêm uma vantagem significativa sobre a transformada de Fourier, que fornece apenas informações globais sobre as frequências (escalas) do sinal analisado, uma vez que o sistema de funções utilizadas (expoente complexo ou senos e cossenos) é definido em intervalo infinito.
3. As listagens acima, escritas na linguagem Python de alto nível distribuída gratuitamente, permitem selecionar funções para wavelets que atendem aos requisitos especificados. No entanto, é adicionalmente necessário levar em consideração todos os principais sinais de wavelets.
Os principais sinais da wavelet
Limitação. O quadrado da norma da função deve ser finito:
left | psi right |2= int infty− infty left| psi(t) right|2dt< infty . 2)
Localização O VP, em contraste com a transformação de Fourier, usa uma função inicial localizada no tempo e na frequência. Para fazer isso, basta que as seguintes condições sejam atendidas:
left| psi(t) right| leqC(1+ left|t right|)−1− varepsilon e
left|S psi( omega) right| leqC(1+ left| omega right|)−1− varepsilon às
varepsilon>0 (3)
Por exemplo, uma função delta
delta(t) e a função harmônica não satisfazem as condições necessárias para a localização simultânea nos domínios de tempo e frequência.
Média zero. O gráfico da função original deve oscilar (alternando) em torno de zero no eixo do tempo e ter área zero:
int infty− infty psi(t)dt=0 . 4)
A partir dessa condição, fica clara a escolha do nome "wavelet" - uma pequena onda.
Área de função igual a zero
psi(t) , ou seja, momento zero, leva ao fato de a transformada de Fourier
S psi( omega) esta função é igual a zero para
omega=0 e tem a forma de um filtro passa-banda. Para vários valores (a), este será um conjunto de filtros passa-banda.
Muitas vezes, para aplicativos, é necessário que não apenas zero, mas todos os primeiros n momentos sejam iguais a zero:
int infty− inftytn psi(t)dt=0 . (5)
As n-ésimas wavelets permitem analisar a estrutura mais fina (alta frequência) do sinal, suprimindo seus componentes que mudam lentamente.
Feito por você mesmo. Uma característica do VP é sua auto-similaridade. Todas as wavelets de uma família específica
psiab(t) têm o mesmo número de oscilações que a mãe wavelet
psi(t) , desde que obtido por meio de transformações de escala (a) e deslocamento (b).
Transformada de wavelet contínua
Transformada de wavelet contínua (integral) (NVP ou WT - transformação de wavelet contínua). Construímos a base
psiab(t) usando transformações contínuas de escala (a) e transferências (b) da wavelet mãe
psi(t) com valores arbitrários dos parâmetros base aeb na fórmula (1).
Então, por definição, o NVP direto (análise) e reverso (síntese) (ou seja, PNVP e ONVP) do sinal S (t) são escritos da seguinte forma:
Ws(a,b)=(S(t), psiab(t))= frac1 sqrta int infty− inftyS(t) psi left( fractba right)dt (6)
S(t)= frac1C psi int infty− infty int infty− inftyWs(a,b) psiab(t) fracdadba2 (7)
onde
C psi - coeficiente de normalização,
C psi= int infty− infty left| psi( omega) right|2 left| omega right|−1d omega< inftyonde: (•, •) é o produto escalar dos fatores correspondentes,
mathbf psi( omega) - Transformada de Fourier de uma wavelet
psi(t) . Para wavelets ortonormais
C psi=1 .
Resulta de (6) que o espectro de wavelets
Ws(b,a) (espectro wavelet, ou espectro de escala de tempo), diferentemente do espectro de Fourier (espectro único), é uma função de dois argumentos: o primeiro argumento a (escala de tempo) é semelhante ao período de oscilação, ou seja, é inverso à frequência e o segundo b –– é semelhante ao deslocamento do sinal ao longo do eixo do tempo.
Note-se que
Ws(b,a0) caracteriza a dependência do tempo (em
a=a0) , enquanto as dependências
Ws(a,b0) é possível combinar a dependência de frequência (por
b=b0 )
Se o sinal estudado S (t) é um único pulso de duração
tauu concentrado no bairro
t=t0 , seu espectro de wavelets terá o maior valor nas proximidades do ponto com coordenadas
a= tauu,b=t0 .
Métodos de apresentação Ws(b,a) pode ser diferente. Spectrum
Ws(b,a) é uma superfície no espaço tridimensional. No entanto, muitas vezes em vez da imagem da superfície, sua projeção no plano ab é apresentada com níveis iso (ou figuras de várias cores), que permitem rastrear a mudança na intensidade das amplitudes do EP em diferentes escalas (a) e no tempo (b).
Além disso, eles representam linhas de extremos locais dessas superfícies, o chamado esqueleto (esqueleto), que revela a estrutura do sinal analisado.
Transformada de wavelet contínua ao determinar o espectro de wavelet com base na wavelet mãe - “chapéu mexicano”
Outras wavelets maternas usadas para NVP também são usadas:

O VP contínuo é amplamente utilizado no processamento de sinais. Em particular, a análise wavelet (VA) oferece oportunidades únicas para reconhecer características locais e "sutis" de sinais (funções), o que é importante em muitas áreas de engenharia de rádio, comunicações, rádio eletrônica, geofísica e outros ramos da ciência e tecnologia. Vamos considerar essa possibilidade com alguns exemplos simples.
Oscilação harmônica.O sinal tem a forma:
s(t)=Asin( omegat− phi)onde:
A=1V, omega= frac2 piT= frac2 pi50, psi=0Função de formação de wavelet:
MHAT(t):= fracd2dt2exp(−t2/2) ,
Wavelets:
psi(a,b,t)= frac1 sqrtaMHAT left( fract−ba right) ,
Espectro de wavelets: N: = 256, a: = 1..30, b: = 0..50,
W(a,b):= intN−N psi(a,b,t)s(t)dt,Nab:=W(a,b) .
Listagem do programa from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 T=50 def S(t): return sin(2*pi*t/T) plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,100,1)] x=[t for t in arange(0,100,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49,49) fig = plt.figure("- : ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z,100) plt.show()
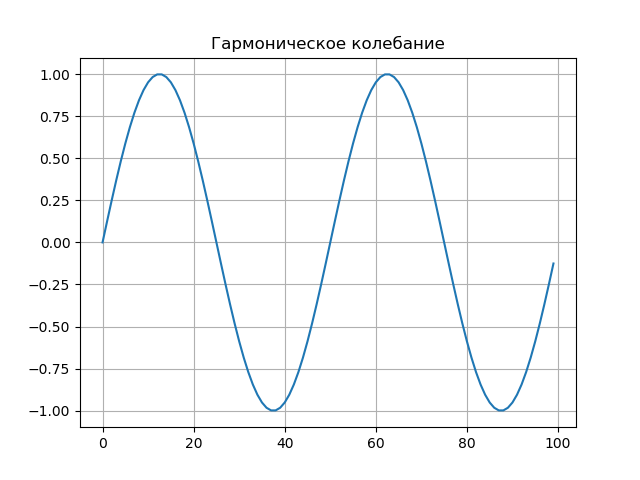
Gráfico de sinal.

Gráfico de um espectro de dois parâmetros
Nab=W(ab) exibido como uma superfície no espaço tridimensional.

Note-se que a seção W (a, b) para a escala de tempo
a=a0 caracteriza a oscilação inicial s (t). Além disso, sua amplitude é máxima em
a0:1/ omega . Dependências
W(a0,b0) pode corresponder ao espectro atual de oscilações em
b=b0 .
A soma de duas oscilações harmônicas.O sinal tem a forma:
s(t):=A1sin( omega1t)+A2sin( omega2t)onde:
A1=A2=1V, omega1= frac2 piT1, omega2= frac2 piT2,T1=50s,T2=10s .
MHAT(t):= fracd2dt2 left[e−t2/2 right] , N: = 256,
psi(a,b,t):=MHAT left( fractba right),W(a,b):= intN−N psi(a,b,t)f(t)dt , a: = 1 ... 30, b: = 0 ... 50,
Nab:=W(a,b) .
Listagem do programa from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): return sin(2*pi*t/10)+sin(2*pi*t/50) plt.figure(' ') plt.title(' ', size=12) y=[S(t) for t in arange(0,250,1)] x=[t for t in arange(0,250,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49, 49) fig = plt.figure("-:2- ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z, 100) plt.figure() q=[w(2,i) for i in y] p=[i for i in y] plt.plot(p,q,label='w(2,b)') q=[w(15,i) for i in y] plt.plot(p,q,label='w(15,b)') q=[w(30,i) for i in y] plt.plot(p,q,label='w(30,b)') plt.legend(loc='best') plt.grid(True) plt.figure() q=[w(i,13) for i in x] p=[i for i in x] plt.plot(p,q,label='w(a,13)') q=[w(i,17) for i in x] plt.plot(p,q,label='w(a,17)') plt.legend(loc='best') plt.grid(True) plt.show()

Gráfico de sinal.
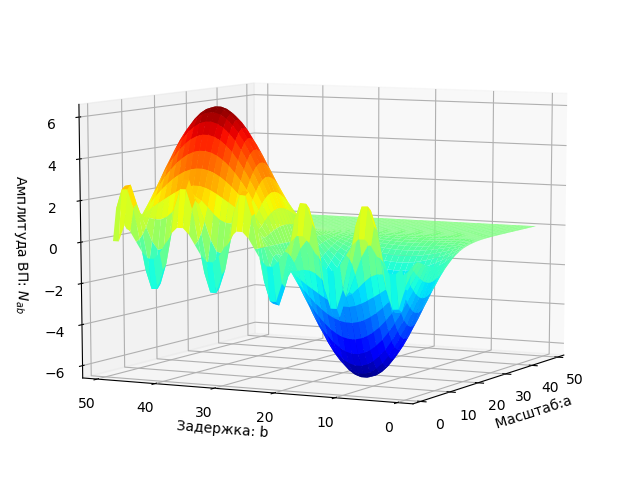
O gráfico do espectro de dois parâmetros W (a, b) é exibido como uma superfície no espaço tridimensional.
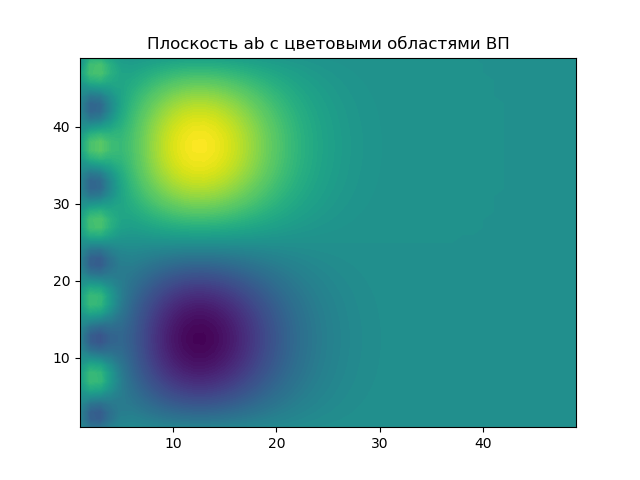
O plano dos parâmetros a, b no qual os resultados do EP são destacados em áreas coloridas.

O gráfico mostra as “seções transversais” do espectro da wavelet para dois valores do parâmetro a. Com um parâmetro relativamente pequeno da escala de tempo a, por
a1=2(a1:1/ omega2) , a seção transversal do espectro carrega informações apenas sobre o componente de alta frequência do sinal, filtrando (suprimindo) seu componente de baixa frequência.
À medida que aumenta, a extensão da função base
psi( fract−ba) , portanto, estreitando seu espectro e estreitando a largura de banda da "janela" de frequência. Como resultado, quando
a2=15(a2:1/ omega1) a seção transversal do espectro é apenas um componente de baixa frequência do sinal.
Com um aumento adicional em a, a faixa da janela ainda diminui e o nível desse componente de baixa frequência diminui para um componente constante (para um> 25), que é igual a zero para o sinal analisado.

O gráfico mostra as seções do espectro wavelet W (a, b) caracterizando
espectro de sinal atual em
b1=13 e
b2=17 . O espectro do sinal considerado, em contraste com o harmônico, contém um componente de alta frequência na região de pequenos valores da escala de tempo a (a: 1..3), que corresponde ao segundo componente do sinal
A2sin( omega2t) .
Momento retangular.U:=5,t0:=20, tau:=60s(t):= beginvmatrixU,set0 leqt leqt0+ tau0,casocontrário endvmatrixMHAT(t):= fracd2dt2exp left( frac−t22 right)N:=128, psi(a,b,t):=MHAT left( fractba right),W(a,b):= intN−N psi(a,b,t)f(t)dta:=1..50,b:=0..100,Nba:=W(a,b)Listagem do programa from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): U=5;t0=20;tau=60 if t0<=t<=t0+tau: return U else: return 0 plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,120,1)] x=[t for t in arange(0,120,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,100,1) y = arange(1,100,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(99, 99) fig = plt.figure("3D- ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z,100) plt.show()
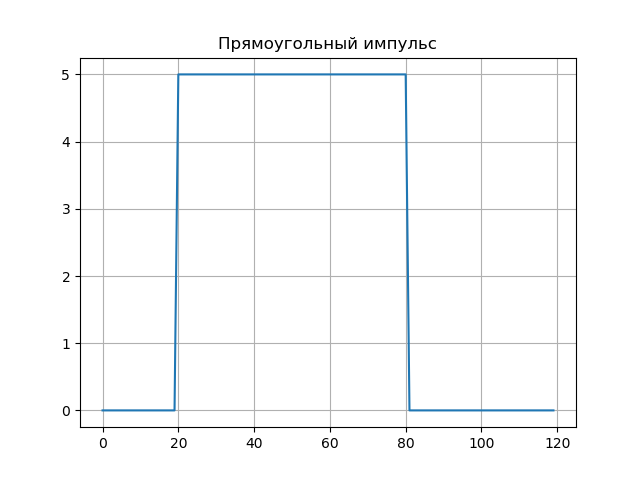


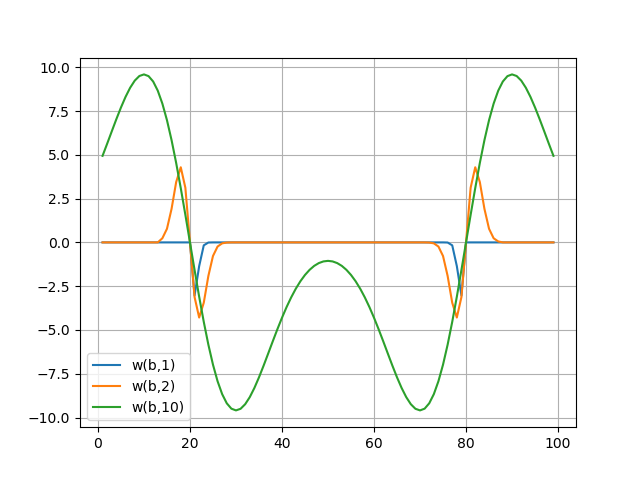
Os espectros da wavelet são mostrados em gráficos, o espectro da wavelet transmite bem as características sutis do sinal - seus saltos nas amostras b = 20 eb = 80 (para a: 1..10).
Conclusões
Esta publicação é de natureza educacional, fornece informações básicas sobre a análise de wavelets em geral, e exemplos simples na linguagem de programação de alto nível distribuída gratuitamente Python mostram os recursos da análise contínua de wavelet com extensa visualização gráfica em 3D e 2D.
PS O autor não diminui as vantagens incondicionais da análise de wavelets usando o Matlab, tanto em termos de número de wavelets quanto de velocidade. Mas em Python ainda há espaço para desenvolvimento adicional: scipy.signal e PyWavelets.