Todos na indústria de TI sabem como é difícil avaliar o prazo de um projeto. É difícil avaliar objetivamente quanto tempo levará para resolver uma tarefa difícil. Uma das minhas teorias favoritas é que este é apenas um artefato estatístico.

Suponha que você avalie um projeto em 1 semana. Suponha que haja três resultados igualmente prováveis: levará meia semana ou uma semana ou duas semanas. O resultado médio é realmente o mesmo que a estimativa: 1 semana, mas o valor médio (também conhecido como valor médio, também conhecido como valor esperado) é 7/6 = 1,17 semanas. A pontuação é realmente calibrada (imparcial) para a mediana (que é 1), mas não para a média.

Um modelo razoável para o “fator de inflação” (tempo real dividido pelo tempo estimado) seria algo como uma distribuição lognormal . Se a estimativa for igual a uma semana, simulamos o resultado real como uma variável aleatória distribuída de acordo com a distribuição lognormal por cerca de uma semana. Em tal situação, a mediana da distribuição é exatamente uma semana, mas o valor médio é muito maior:



Se tomarmos o logaritmo do coeficiente de inflação, obtemos uma distribuição normal simples com um centro de cerca de 0. Isso assume um coeficiente de inflação mediano de 1x e, como você espera, lembre-se de log (1) = 0. No entanto, em vários problemas, pode haver diferentes incertezas em torno de 0. Podemos modelá-los alterando o parâmetro σ, que corresponde ao desvio padrão da distribuição normal:



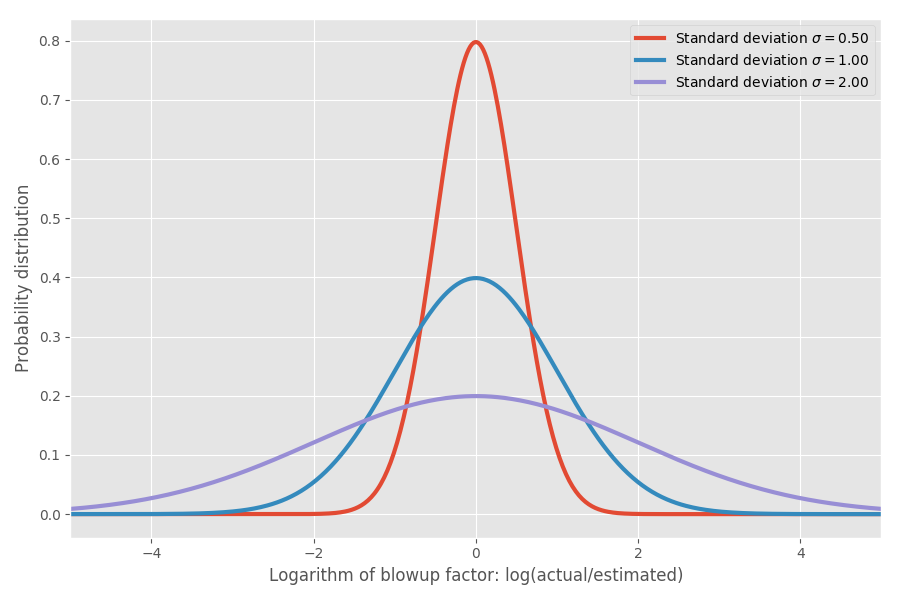
Apenas para mostrar os números reais: quando log (real / estimado) = 1, então o coeficiente de inflação exp (1) = e = 2,72. É igualmente provável que o projeto se estenda para exp (2) = 7,4 vezes e que termine em exp (-2) = 0,14, ou seja, 14% do tempo estimado. Intuitivamente, o motivo pelo qual a média é tão grande é que as tarefas executadas mais rapidamente do que o previsto não podem compensar as tarefas que demoram muito mais do que o previsto. Estamos limitados a 0, mas não limitados na outra direção.

Isso é apenas um modelo? Eu gostaria que você pudesse! Mas em breve chegarei aos dados reais e, em alguns dados empíricos, mostrarei que, de fato, é bastante consistente com a realidade.

Estimando cronogramas de desenvolvimento de software

Até agora, tudo bem, mas vamos realmente tentar entender o que isso significa em termos de estimativa de cronogramas de desenvolvimento de software. Suponha que analisemos um plano de 20 projetos de software diferentes e tentemos avaliar quanto tempo levará para concluir todos eles .

É aqui que a média se torna decisiva. As médias somam, mas não há mediana. Portanto, se quisermos ter uma idéia de quanto tempo levará para concluir a soma de N projetos, precisamos examinar o valor médio. Suponha que tenhamos três projetos diferentes com o mesmo σ = 1:


Observe que as médias são somadas e 4,95 = 1,65 * 3, mas outras colunas não.

Agora vamos adicionar três projetos com sigma diferente:


As médias ainda estão tomando forma, mas a realidade não chega nem perto da ingênua estimativa de três semanas que você poderia esperar. Observe que um projeto altamente incerto com σ = 2 domina o restante no tempo médio de conclusão. E para o percentil 99, ele não apenas domina, mas literalmente absorve todos os outros. Podemos dar um exemplo maior:


Novamente, a única tarefa desagradável é predominante no cálculo da estimativa, pelo menos em 99% dos casos. Mesmo no tempo médio, um projeto louco leva, em última análise, cerca da metade do tempo gasto em todas as tarefas, embora eles tenham valores semelhantes em termos de mediana. Por simplicidade, presumi que todas as tarefas têm a mesma estimativa de tempo, mas incertezas diferentes. A matemática é salva quando os termos mudam.

É engraçado, mas há muito tempo sinto esse sentimento. Adicionar classificações raramente funciona quando você tem muitas tarefas. Em vez disso, descubra quais tarefas têm maior incerteza: essas tarefas geralmente dominam o tempo médio de execução.

O diagrama mostra a média e o percentil 99 em função da incerteza (σ):



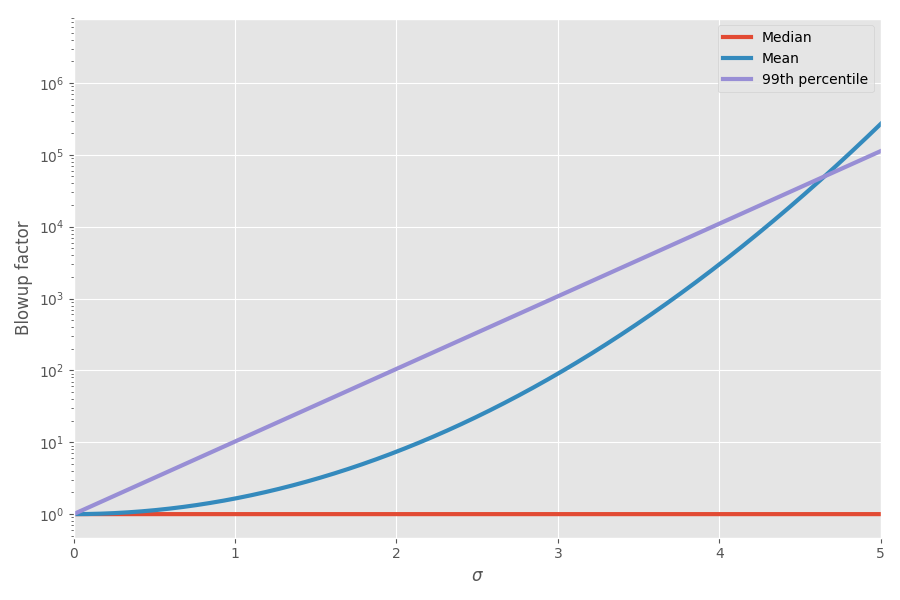
Agora a matemática explicou minhas sensações! Comecei a levar isso em consideração ao planejar projetos. Eu realmente acho que adicionar estimativas dos prazos para as tarefas é muito enganador e cria uma imagem falsa de quanto tempo o projeto inteiro levará, porque você tem essas tarefas malucas e distorcidas que, no final das contas, levam o tempo todo.

Onde está a evidência empírica?

Durante muito tempo, guardei-o no meu cérebro na seção "modelos de brinquedos curiosos", às vezes pensando que essa é uma ilustração clara do fenômeno do mundo real. Mas um dia, vagando pela rede, encontrei um conjunto interessante de dados sobre a avaliação do tempo dos projetos e o tempo real para concluí-los. Ficção!

Vamos fazer um gráfico de dispersão rápida do tempo estimado e real:



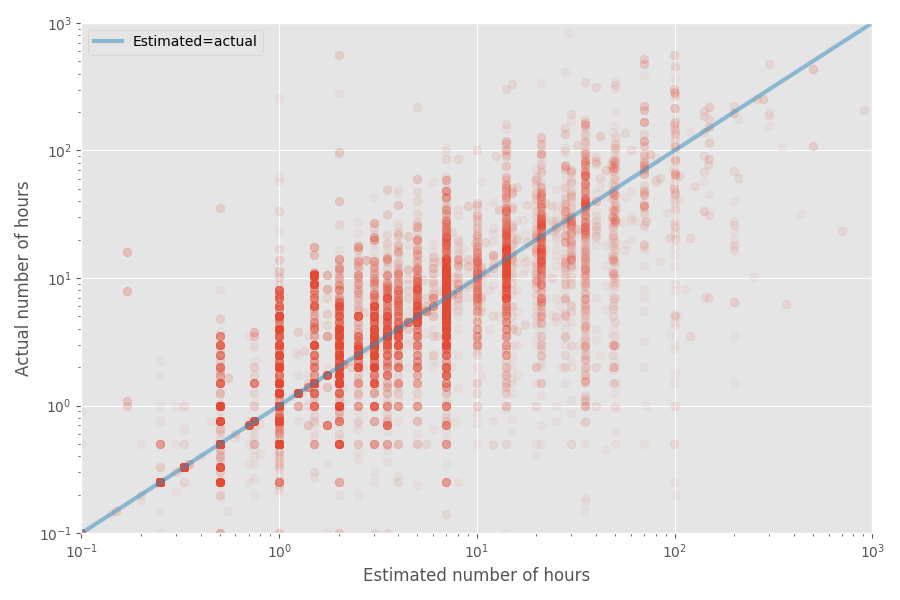
A taxa média de inflação para esse conjunto de dados é de 1X, enquanto o coeficiente médio é de 1,81x. Novamente, isso confirma o palpite de que os desenvolvedores avaliam bem a mediana, mas a média é muito maior.

Vejamos a distribuição do coeficiente de inflação (logaritmo):



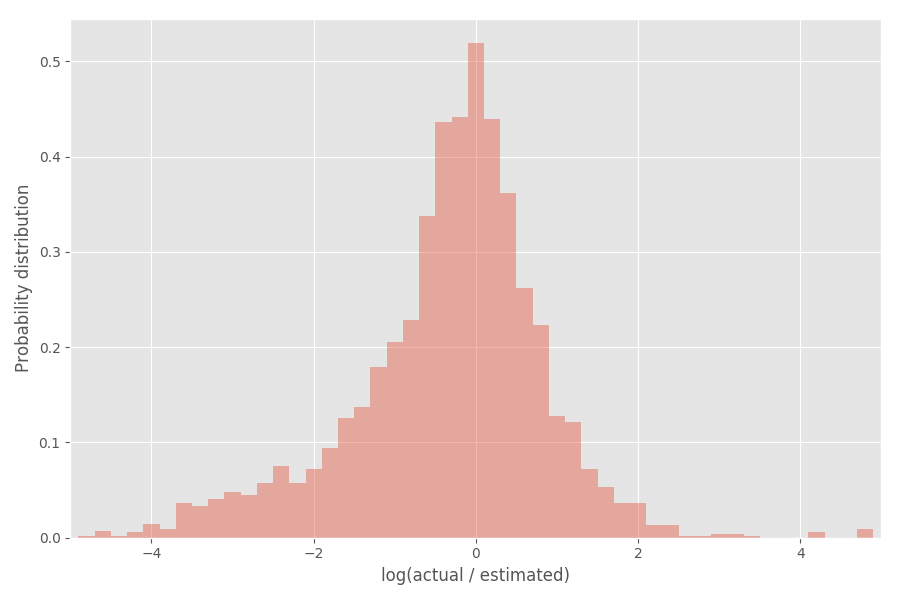
Como você pode ver, ele está muito bem centrado em torno de 0, onde o coeficiente de inflação exp (0) = 1.

Pegue as ferramentas estatísticas

Agora vou sonhar um pouco com estatísticas - não hesite em pular esta parte se não for interessante para você. O que podemos concluir dessa distribuição empírica? Você pode esperar que os logaritmos da taxa de inflação sejam distribuídos de acordo com a distribuição normal, mas isso não é inteiramente verdade. Observe que σ em si é aleatório e varia para cada projeto.

Uma maneira conveniente de modelar σ é que eles são selecionados a partir da distribuição gama inversa . Se assumirmos (como antes) que o logaritmo dos coeficientes de inflação é distribuído de acordo com a distribuição normal, a distribuição "global" dos logaritmos dos coeficientes de inflação termina com a distribuição de Student .

Aplicamos a distribuição dos alunos à anterior:



Decentemente converge, na minha opinião! Os parâmetros de distribuição dos alunos também determinam a distribuição gama inversa dos valores de σ:



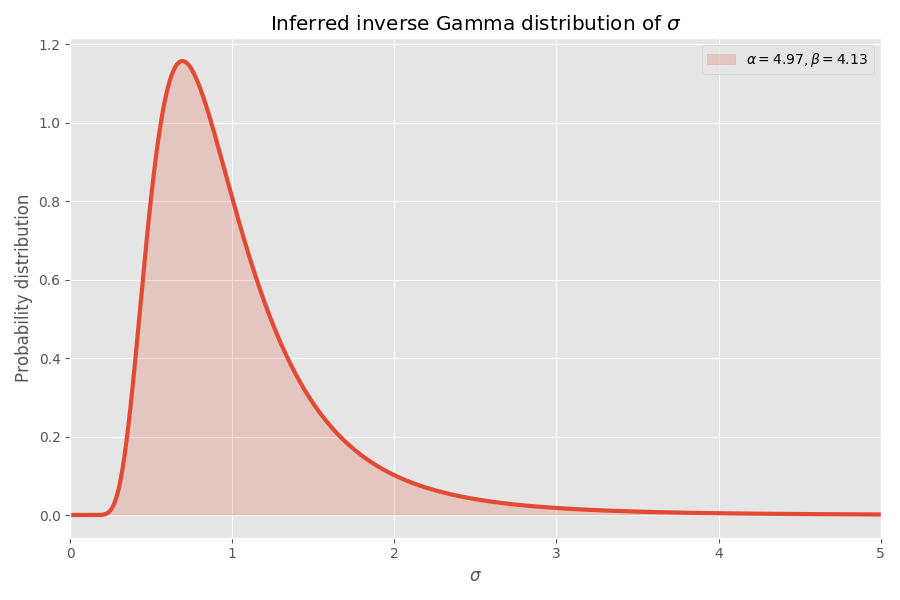
Observe que os valores de σ> 4 são muito improváveis, mas quando ocorrem, causam uma explosão média de vários milhares de vezes.

Por que as tarefas de software sempre levam mais tempo do que você pensa

Supondo que este conjunto de dados seja representativo do desenvolvimento de software (duvidoso!), Podemos tirar mais algumas conclusões. Temos parâmetros para a distribuição de Alunos, para que possamos calcular o tempo médio necessário para concluir a tarefa sem saber σ para esta tarefa.

Embora a taxa média de inflação desse ajuste seja de 1x (como antes), a taxa de inflação de 99% é de 32x, mas se você atingir o percentil 99,99, são 55 milhões ! Uma interpretação (gratuita) é que algumas tarefas são impossíveis. De fato, esses casos extremos têm um impacto tão grande na média que a taxa média de inflação de qualquer tarefa se torna infinita . Esta é uma notícia muito ruim para quem tenta cumprir prazos!

Sumário

Se meu modelo estiver correto (big if), eis o que podemos descobrir:

• As pessoas estimam bem o tempo mediano para concluir uma tarefa, mas não a média.
  
• O tempo médio é muito maior que a mediana devido ao fato de a distribuição estar distorcida (distribuição lognormal).
  
• Quando você adiciona notas para n tarefas, as coisas pioram.
  
• Tarefas da maior incerteza (em vez disso, do maior tamanho) geralmente podem dominar no tempo médio necessário para concluir todas as tarefas.
  
• O tempo médio de execução de uma tarefa sobre a qual não sabemos nada é realmente infinito .

Anotações

• Obviamente, as descobertas são baseadas em apenas um conjunto de dados que eu encontrei na Internet. Outros conjuntos de dados podem fornecer resultados diferentes.
  
• Meu modelo, é claro, também é muito subjetivo, como qualquer modelo estatístico.
  
• Eu ficaria feliz em aplicar o modelo a um conjunto de dados muito maior para ver quão estável ele é.
  
• Sugeri que todas as tarefas sejam independentes. De fato, eles podem ter uma correlação que tornará a análise muito mais irritante, mas (acho) acabam com conclusões semelhantes.
  
• A soma dos valores distribuídos normalmente do log não é outro valor distribuído normalmente do log. Esse é o ponto fraco dessa distribuição, pois você pode argumentar que a maioria das tarefas é simplesmente a soma das subtarefas. Seria bom se nossa distribuição fosse sustentável .
  
• Eu removi pequenas tarefas do histograma (o tempo estimado é menor ou igual a 7 horas), pois elas distorcem a análise e houve uma onda estranha de exatamente 7.
  
• O código está no Github , como de costume.