Boa tarde, querido leitor! Este é o segundo artigo traduzido em uma série de artigos sobre a criação do mecanismo de física de Chris Hecker. Se você ainda não se familiarizou com o primeiro , recomendo fazer isso, porque tudo ficará imediatamente claro. Muito obrigado por apoiar a primeira tradução: é muito encorajador trabalhar mais e mais! Boa leitura!

Física, Parte 2, Efeitos Angulares

Eu só queria voltar a porta com algo pesado para que um intruso não entrasse. Estou pedindo muito? Quero que o carro dele role e exploda em um lugar específico. Quero que as engrenagens enormes atolem antes que me achatem. E quero construir às pressas algo que se pareça com um balanço, para catapultar um presente bonito e brilhante através da muralha do castelo. Quem pode me impedir de traduzir tudo isso em realidade? Você supõe que meu oponente esteja no mundo do jogo, mas na realidade - um programador do mecanismo físico, porque tudo isso é baseado no efeito angular. Você pode contar com os dedos aqueles jogos em que os efeitos de canto são implementados, sem mencionar a localização de pelo menos um no qual isso é feito corretamente.

A principal razão pela qual efeitos angulares (ou rotacionais) não são implementados nos jogos atualmente é porque os programadores acreditam que a física que descreve o movimento rotacional é muito complicada para entender e traduzir em realidade. Nas aulas de física no ensino médio (onde todos aprendemos a segunda lei de Newton), eles geralmente não falam sobre efeitos rotacionais, e não é totalmente óbvio como passar da força aplicada ao objeto para a rotação desse objeto. Obviamente, a dinâmica do movimento rotacional é um pouco mais difícil de entender do que a dinâmica do movimento linear, mas é mais simples do que parece. Qualquer pessoa que possa criar um mecanismo físico de acordo com o material apresentado no primeiro artigo do ciclo também conseguirá incluir os efeitos angulares descritos neste artigo. Espera-se que, após a publicação deste artigo, o mundo fique repleto de jogos que usem todas as possibilidades e vantagens dos efeitos de canto, ou pelo menos você pode criar um jogo no qual, quando se incline, atire na perna do seu amigo em uma batalha mortal.

Breve repetição

Apesar de cada um dos meus artigos sobre um tópico único, eu sempre reler o que escrevi anteriormente, para entender onde eu acabei. Acabei de assistir meu primeiro artigo sobre física e estou encantado: conseguimos aprender muito e, além disso, nunca escrevemos um código de programa ou lemos literatura adicional! Antes de começar, vamos atualizar o material do último artigo.



A Tabela 1 contém as conclusões mais importantes para a dinâmica dos sólidos. Segue-se da Equação 1 que o vetor de coordenadas (r), o vetor de velocidade (v) e o vetor de aceleração (a) são relacionados por derivadas (e por integrais, se lermos na ordem inversa). Como lembrete, marcamos a diferenciação de tempo por um primo (r '). r 'é o mesmo que dr / dt e r' 'é o mesmo que a derivada da segunda vez. Da Equação 2, segue-se que a força está associada a um momento linear (o produto de massa e velocidade), massa e aceleração. A definição do centro de massa pode ser obtida na Equação 3 (este é o ponto em que todas as massas e distâncias se equilibram). A Equação 4 afirma que o momento linear total de um sólido é a soma de todos os seus momentos, que, para nossa sorte, são simplesmente iguais ao momento do centro de massa (CM). A equação 5 é uma verdadeira jóia. Ele usa a Equação 4 para demonstrar que a aceleração do centro de massa de um objeto está relacionada à força total (o vetor da soma de todas as forças que atuam no objeto em um determinado momento) através de uma quantidade escalar, a massa do objeto.

Para resumir tudo o que é descrito no primeiro artigo: aprendemos que a força total que atua no nosso centro de massa é igual à soma de todas as forças aplicadas ao corpo (incluindo a força da gravidade, a carroça do vilão, uma explosão nas proximidades, o impulso do nosso motor etc.) .). Depois disso, dividimos esse vetor de soma pela massa corporal, a fim de obter a aceleração do CM e, em seguida, integramos a aceleração do tempo para obter a velocidade e a coordenada do corpo.

A equação 5 é apenas uma obra-prima! Você verá que não há um conceito de pontos de aplicação de forças no corpo, e este é um ponto-chave para determinar como o corpo irá girar sob sua ação. A equação 5 está correta. De fato, é excelente para encontrar aceleração linear. Estamos perdendo metade da batalha. Mas as primeiras coisas primeiro ...

Qual é o seu ângulo?

No primeiro artigo, a rotação foi ignorada; portanto, precisamos apenas de um vetor de raio e sua derivada para descrever a configuração do nosso corpo em 2D. Agora, vamos adicionar outro valor cinemático, a orientação (indicada pela letra maiúscula ômega - Ω), para trabalhar com efeitos de canto. Para definir Ω, precisamos escolher o sistema de coordenadas em relação ao sólido e o sistema de coordenadas do mundo do jogo, e o valor de Ω será igual à diferença de ângulos entre eles em radianos, como mostra a Figura 1.



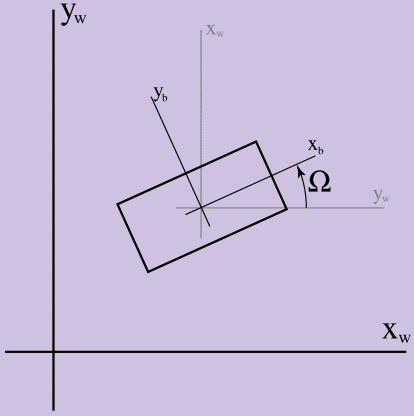Figura 1. Definição de Ω

Na figura, os eixos xw, yw são os eixos de coordenadas do mundo do jogo e xb, yb são os eixos de coordenadas do sólido. Ω é maior que 0 se contado no sentido anti-horário. É importante esclarecer aqui por que estudamos a dinâmica do mundo bidimensional antes de passar para o tridimensional: a orientação em 2D é uma quantidade escalar (o ângulo entre os sistemas de coordenadas em radianos), enquanto a determinação da orientação no mundo tridimensional é muito mais difícil.

À medida que o corpo gira, o valor de Ω muda. Essa mudança nos leva a outra cinemática - a velocidade angular (indicada pela letra minúscula ômega - ω). Em contraste com a velocidade coordenada e linear do corpo, não denotamos a velocidade angular da seguinte forma - Ω '. Entretanto, às vezes denotamos a derivada da velocidade em relação ao tempo, ou aceleração angular, como ω '(esse é outro valor cinemático) ou como α (alfa em minúsculas). Não me culpe: eu não inventei todas essas designações; e em todos os livros que li há pequenas discrepâncias. Nossa contraparte angular da Equação 1 é:

$$$$ display $$ {d ^ 2 Ω \ over {dt ^ 2}} = {dω \ over {dt}} = ω '= α $$ display $$

Equação 6

Como na Equação 1, diferenciamos ω no tempo para obter α; e se integrarmos α ao longo do tempo, obteremos ω etc. Tudo por analogia com o artigo anterior: conhecendo a aceleração angular de α, podemos integrá-la duas vezes para obter uma nova orientação. Mas o ponto principal aqui é saber o valor de α.

Como você pode imaginar, nosso objetivo para este artigo é derivar um análogo angular para cada uma das equações lineares da Tabela 1 e, considerando as equações lineares e angulares e a força aplicada ao objeto, podemos calcular sua aceleração linear ae aceleração angular α. Finalmente, podemos integrar numericamente essas acelerações para encontrar novas posições e orientações de nossos corpos.

Para começar, conectaremos quantidades lineares e angulares. E esse é um truque bastante óbvio no qual a velocidade angular é usada. Ao calcular em dinâmica, geralmente precisamos encontrar a velocidade de um ponto arbitrário em um objeto. Por exemplo, quando calculamos colisões de sólidos, precisamos saber a velocidade dos pontos de colisão para entender o quanto eles se batem. Se nosso corpo não gira, a velocidade de cada ponto do corpo é a mesma. Podemos simplesmente monitorar a velocidade do centro de massa do corpo, e isso será suficiente. Enquanto que, se nosso corpo gira, cada ponto desses corpos pode ter uma velocidade diferente. Obviamente, não podemos calcular a velocidade de um número infinito de pontos do nosso corpo rígido; portanto, precisamos de uma solução diferente e melhor.

Um dos métodos simples usados ​​para encontrar a velocidade linear de qualquer ponto dentro de um objeto usa a velocidade angular do objeto. Considere o caso em que o corpo gira apenas em torno de um ponto fixo O, sem alterar a coordenada do corpo. Ou seja, o corpo gira, mas não se move. A partir da Equação 7, segue-se como calcular a velocidade do ponto B de um corpo em rotação:

$$$$ exibição $$ v ^ B = ωr ^ {OB} _⟂ $$ exibição $$

Equação 7

Precisamos esclarecer alguns pontos na Equação 7, vamos dedicar algum tempo a isso. Primeiro, eu uso a indexação superior para mostrar qual parâmetro pertence a esses pontos, então v ^ B é o vetor de velocidade do ponto B do nosso corpo. Da mesma forma, r ^ OB denota um vetor desenhado do centro de rotação do nosso corpo O até o ponto B. Uma letra invertida engraçada T é um "operador perpendicular" que atua sobre um vetor (como o vetor r na Equação 7) e o gira 90 graus no sentido anti-horário setas. Em outras palavras, é construído um novo vetor perpendicular ao antigo. Em um mundo bidimensional, um vetor perpendicular a (x, y) é apenas (-y, x). Você pode verificar facilmente minhas palavras em uma folha de papel milimetrado. Vamos falar mais sobre isso. A magnitude do vetor perpendicular é determinada pela velocidade angular ω e define a velocidade linear v ^ B. Em russo, a Equação 7 mostra que a velocidade de um ponto de um corpo em rotação é calculada multiplicando o vetor perpendicular desenhado do centro de rotação pela velocidade angular. Como eu entendo isso? Bem, eu li sobre isso no livro, mas é óbvio que essa explicação não é suficiente, então provamos que isso é verdade.

Vamos provar a verdade das conclusões da Equação 7 em duas etapas. Primeiro, provamos que o valor do vetor de velocidade resultante está correto; então - que sua direção está correta. Para a primeira parte da prova, considere a Figura 2.



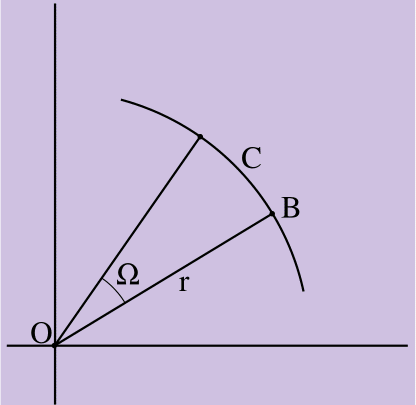Figura 2. C = Ωr

A Figura 2 mostra a rotação do ponto B por um ângulo igual a Ω radiano no sentido de rotação de um corpo rígido com um vetor de raio de comprimento r direcionado do centro de rotação do corpo O para o ponto B. B passou o comprimento do arco C, onde C = fromr da definição de radianos. (Uma medida radiana de um ângulo é uma medida de um arco delimitada por um raio de um círculo. A circunferência de um círculo é C = 2πr porque a medida de radiano de um arco de um círculo é 2π [ou 360 graus]).

A velocidade de um ponto é uma mudança na sua coordenada no tempo. Portanto, podemos encontrar a velocidade do ponto B - em outras palavras, a magnitude do vetor de velocidade - diferenciando as equações de movimento em relação ao tempo. C = Ωr é a equação do movimento.

$$

$${d ()r) \ over {dt}} = {dΩ \ over {dt}} r = ωr$$

O raio é retirado do sinal de diferenciação, porque é uma constante (o ponto B simplesmente gira, sem deslocamento linear), e a derivada de tempo Ω é ω da equação 6. Portanto, a magnitude do vetor B é o vetor de velocidade ωr.

Considerando a Equação 7, notamos que a magnitude do vetor de velocidade está correta, uma vez que a perpendicular não afeta o comprimento do vetor e r ^ OB é um vetor de raio direcionado de O a B. Fuh, estamos no meio do caminho.

Para verificar se a direção do vetor de velocidade na Equação 7 está correta, vamos começar assegurando que o vetor de velocidade seja perpendicular ao vetor de raio. Essa suposição é compreensível intuitivamente, porque um ponto que gira em torno de algum outro ponto pode apenas se mover perpendicular ao vetor entre esses pontos. Ele não pode se aproximar do centro de rotação ou se afastar dele, ou esse movimento simplesmente deixará de ser rotação. Podemos apoiar nossa suposição com cálculos para vetores, mas estou preso em uma certa estrutura para o volume do artigo, portanto, assumiremos que nossa suposição está correta. (Se você deseja provar isso sozinho, diferencie o produto escalar de um vetor de comprimento fixo por si mesmo.)

Finalmente, devemos garantir que o vetor esteja marcado corretamente, porque a figura mostra dois vetores de comprimento igual perpendicular ao raio: ve -v. Como o valor de Ω é medido no sentido anti-horário, ω> 0 quando o ponto gira no sentido horário. Os pontos perpendiculares no sentido horário, assim como o vetor raio. A Figura 3 mostra as conclusões da Equação 7:



Figura 3. Relação entre velocidade linear e angular

Suplemente a Equação 7 para descrever a rotação dos corpos em movimento. Consideramos o movimento de um corpo sólido como um simples movimento do centro de rotação do corpo e uma simples rotação do resto do corpo em torno deste ponto. Para quem está interessado, esse é o teorema de Schal sobre a classificação de movimentos.

O teorema de Chall divide nosso movimento em dois componentes - linear e angular. Seja o único ponto móvel do centro de rotação do corpo O, então usamos ω para calcular a rotação em torno do ponto O, e isso nos dá a forma geral da Equação 7:

$$$$ exibição $$ v ^ B = v ^ O + ωr ^ {OB} _⟂ $$ exibição $$

Equação 9

A equação 9 diz que podemos calcular a velocidade de qualquer ponto de um corpo em movimento usando a velocidade linear do centro de rotação do corpo e, além disso, a velocidade adquirida durante a rotação do corpo.

Razão do nosso impulso

Agora podemos escrever um análogo angular da Equação 2, a equação da força. Começamos determinando o momento angular, L ^ AB de um determinado ponto B, em torno de outro ponto A:

$$

$${L} ^ {AB} = {\ vec r} ^ {AB} \ times {\ vec p} ^ B$$

Equação 10

O momento do momento de um ponto difere do momento linear de um ponto, pois a versão angular da equação leva em consideração a posição do corpo no espaço. Daí resulta que o momento angular de um ponto deve ser medido para um lugar diferente no mundo do jogo, em contraste com o impulso linear, determinado para um determinado ponto (o produto de sua massa e velocidade). Isso é mostrado através da indexação superior na Equação 10. A notação L ^ AB diz que o momento angular é medido para o ponto B a partir do ponto A (centro de rotação do corpo). Imagine uma seta apontando do ponto A ao ponto B. Esta seta é um vetor de raio entre dois pontos, significa r ^ AB. Portanto, o momento angular de um ponto é um produto escalar de um vetor de momento linear e um vetor de raio perpendicular a ele. Essa operação é chamada de “produto escalar com perpendicular” e é um analógico 2D para o produto vetorial 3D, mas discutiremos isso outra vez.

Se você representar graficamente o que se segue da equação 10, no papel - como fiz na Figura 4 -, verá que ele determina a medida de como o momento linear do ponto B “gira em torno” A.



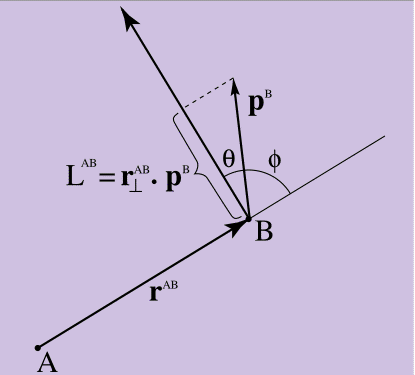Figura 4. Momento do impulso

Tudo está correto se o momento do ponto B apontar diretamente para o ponto A, Equação 10 = 0 (uma vez que a perpendicular a r forma um ângulo reto com p, e o produto escalar será 0). Quanto maior o momento B direcionado perpendicularmente a A, maior o momento. Como pode ser visto na Figura 4, o produto escalar na Equação 10 tem como parâmetro o cosseno do ângulo θ entre a perpendicular r ^ AB a p ^ B. Se você olhar para ele, por outro lado, a magnitude do produto escalar é dada pelo seno do ângulo φ entre os originais, não perpendicular a r ^ AB e p ^ B (o seno é outra chave para desvendar a conexão entre o vetor e o produto escalar). A equação 10 fornece uma medida de quanto do momento do ponto B "parece" na "direção de rotação" em relação ao ponto A.

Além disso, como usamos a derivada do momento linear para determinar a força, usaremos a derivada do momento angular para determinar o gêmeo angular da força - o momento da força (indicado pela letra minúscula tau - τ).

$$

$$τ ^ {AB} = {dL ^ {AB} \ over dt} = {d ({\ vec r} ^ {AB} \ times {\ vec p} ^ B) \ over dt} = \ vec r ^ { AB} \ vezes ma ^ B = \ vec r ^ {AB} \ vezes F ^ B$$

Equação 11

Para economizar espaço, trapacei um pouco na Equação 11, pulando algumas etapas difíceis que envolviam encontrar derivadas. Pelo exposto, segue-se que o momento da força está associado à força em um determinado ponto através de um produto escalar.

Finalmente, obtivemos uma equação dinâmica que usa o ponto de aplicação da força, que anteriormente era ignorado nas equações do momento linear. A Equação 11 usa um produto escalar com uma perpendicular como uma medida de quanto da força aplicada ao ponto B gira em torno do ponto A; essa "força rotacional" é chamada momento de força. A equação 11 permite encontrar o valor numérico do momento da força - e, portanto, o momento angular, se integrarmos o momento da força, conhecendo a força aplicada e o ponto de aplicação.

No entanto, ainda não recebemos a equação da relação entre o momento da força e as magnitudes angulares da cinemática de que precisamos para girar o objeto em torno de seu eixo - como aceleração angular, velocidade angular ou orientação. Portanto, não podemos avançar antes de derivar mais algumas equações.

No momento em que todos esperávamos

Antes de fazermos uma conexão entre a dinâmica e a cinemática, precisamos determinar o momento angular total, por analogia com a forma como determinamos o momento linear total na Equação 4. Não esqueci o equivalente angular para o centro de massa na Equação 3; nós o veremos na equação do momento angular total.

O momento angular total próximo ao ponto A é denotado por L ^ AT e é determinado pela Equação 12:

$$

$$L ^ {AT} = {\ sum _ {i} {} {\ vec r ^ {Ai} \ vezes p ^ i}} = {\ sum _ {i} {\ vec r ^ {Ai} \ vezes m ^ iv ^ i}}$$

Equação 12

A equação 12 é a soma de todos os momentos angulares de todos os pontos do corpo, medidos em relação ao ponto A. No lado direito, usei a definição de momento linear para representar p ^ i como o produto de massa e velocidade (mv). Isso será útil para mim no futuro, a fim de fazer da Equação 12 algo com um caráter aplicado mais pronunciado. A equação diz que, para encontrar o momento angular total para o nosso objeto, é necessário somar o momento angular de todos os seus pontos. Para um corpo sólido composto de faces (e não de pontos separados), é necessário calcular a integral, para uma soma não discreta.

Felizmente, podemos simplificar nossos cálculos introduzindo uma nova quantidade chamada “momento de inércia”, semelhante à forma como introduzimos o centro de massa para simplificar a equação do momento total. Lembre-se de que, graças à Equação 7, podemos encontrar a velocidade de um ponto através da velocidade angular. Seja o ponto A na Equação 12 o centro de rotação da Equação 7, e o índice de soma i na Equação 12 seja o ponto B da Equação 7, então é possível converter a Equação 7 na Equação 12. Obtemos:

$$

$$L^{AT} = \sum _{ i} {\vec r ^{Ai} \times m^i ω \vec r^{Ai}} = ω {\sum _{ i} {m^i \vec r^{Ai} \times \vec r ^{Ai}}} = ω \sum_{ i} {m^i (\vec r ^{Ai})^2} = ωI^A$$

Equação 13

Escreverei a Equação 13 com mais detalhes, passo a passo. Primeiro, substituímos a Equação 7 por 12 para obter a soma na Equação 13. Essa substituição nos permite descrever o momento angular usando velocidade angular. A seguir, tomamos ω para a soma, porque é igual para todos os pontos do sólido (a velocidade angular é determinada para todo o corpo, e não para cada ponto separadamente), e anotamos a massa com o índice i à esquerda, para ver mais claramente o raio do produto escalar -vetores por si mesmos. Esse produto escalar é igual ao quadrado do comprimento do vetor do raio (o produto escalar de qualquer vetor por si só = o quadrado do seu comprimento. Lembre-se de que o operador perpendicular não altera o comprimento do vetor.). Finalmente, escrevemos I ^ A para denotar o momento de inércia em torno do ponto A.

O momento de inércia para um sólido bidimensional é um número extremamente bom, porque os pontos que compõem o corpo não podem mudar sua massa ou se afastar do centro de rotação. Como conseqüência dessas duas propriedades, a soma da Equação 13 é uma constante para cada corpo, para que possamos calculá-la. Falando em russo, I ^ A é a soma das distâncias ao quadrado do ponto A a todos os outros pontos do corpo, e cada uma dessas distâncias é dimensionada de acordo com a massa de cada ponto. Assim como no centro de massa - se o corpo for mais sólido do que composto por pontos discretos, as somas se transformarão em integrais. E o momento de inércia permanecerá o mesmo em magnitude e terá o mesmo significado físico.

Determinar o momento de inércia perto de um ponto é detalhado, mas pense em I ^ A como a medida de quão difícil é girar o corpo em torno do ponto A. Por exemplo, imagine um lápis (lápis plano). Se medirmos o momento de inércia próximo ao centro do lápis, obtemos um certo valor igual à soma dos quadrados das distâncias escaladas de acordo com a massa de cada ponto. Enquanto que, se medirmos a inércia na ponta do mesmo lápis, obtemos um valor maior, pois quanto mais os pontos com massa são removidos, maior o valor dos quadrados de suas distâncias. Aqui, formularemos matematicamente o que é intuitivo para nós: girar um lápis em torno de seu centro é muito mais fácil (leia-se que exige menos esforço) do que girá-lo em torno de uma das extremidades.

Finalmente, estamos prontos para estabelecer uma conexão entre as equações angulares da dinâmica e as equações angulares da cinemática. Se diferenciarmos a Equação 13, obteremos o momento total de força à esquerda e o produto do momento de inércia e aceleração angular à direita (I ^ A é uma constante, colocamos fora do sinal de diferenciação):

$$

$$τ^{AT} = {dL^{AT} \over dt} = {d( I^A ω) \over dt} = I^A ω = I^A α$$

Equação 14

Esta equação é o equivalente angular da Equação 5; de fato, é F = ma para dinâmica angular. Esta é a equação da conexão do momento total de força e a aceleração angular do corpo através do momento escalar de inércia. Se conhecermos o momento de força exercido em nosso corpo, podemos encontrar sua aceleração angular e, em seguida, a velocidade angular e orientação no espaço através da integração - dividindo o momento de força pelo momento de inércia.

Algoritmo dinâmico

Ele dificilmente nos vê através deste turbilhão de equações, mas todas elas são parte integrante. Derivamos equações suficientes para obter a dinâmica magnífica de um mundo bidimensional com forças e momentos de forças arbitrariamente dados movendo e girando nossos objetos. Como usar essas equações? Abaixo está o algoritmo básico:

1. Encontre o valor do centro de massa e o momento de inércia no centro de massa.
2. Defina as coordenadas iniciais do corpo, sua orientação no espaço, suas velocidades lineares e angulares.
3. Leve em consideração todas as forças que atuam no corpo e os pontos de sua aplicação.
4. Encontre a resultante de todas as forças e divida-a pela massa do corpo para encontrar a aceleração linear do centro de massa (Equação 5).
5. , , , ( 11).
6. ( 14).
7. , , ( ).
8. , 3.

No algoritmo acima, existem apenas duas etapas que eu não expliquei. Primeiro, como calcular o momento de inércia na Etapa 1 para um objeto sólido? Em segundo lugar, como resolver o problema com as forças da Etapa 3? A resposta para a primeira pergunta pode ser encontrada em um exemplo de código simples, que deixarei no aplicativo no final deste artigo (você integrará o objeto por sua área). Muitos livros sobre dinâmica contêm o momento calculado de inércia para as formas de objetos freqüentemente encontradas no aplicativo no final, para que você não precise exibi-las a cada vez.

A resposta à pergunta de como calcular as forças da Etapa 3 depende da aplicação, mas darei algumas recomendações gerais. Em primeiro lugar, forças como a gravidade, sempre direcionadas em uma direção (para baixo, no caso da gravidade), não criam um momento de força, porque puxam todos os pontos ao mesmo tempo na mesma direção, embora nós aplicamos essas forças diretamente no centro de massa. Forças semelhantes à força elástica são aplicadas a um certo ponto do objeto; elas criarão um momento de força; portanto, as consideramos no caso geral. Como vimos no primeiro artigo, a força de atrito é a mesma força direcionada na direção oposta à velocidade do corpo.

Você pode criar um modelo físico simples demonstrando a força de atrito e aplicar força ao centro de massa, ou escolher quais partes do objeto aplicarão forças de atrito e fazer isso, o que pode criar um momento de força atuando no objeto. As forças que os corpos experimentam em colisões são um pouco mais difíceis, e nós as conheceremos no próximo artigo. Forças como o impulso de um motor de foguete devem ser consideradas forças com um ponto de aplicação (nesse caso, se um dos motores falhar, você começará a girar em torno de seu eixo até ajustar o volante para equilibrar o momento de força!). Se você deseja algo semelhante aos raios gravitacionais de um OVNI, essa força deve ser calculada como a força da gravidade e não criar um momento de força, ou deve ser aplicada a um ponto específico do objeto,e vai girar em torno deste ponto enquanto se levanta? A escolha é sua. O ponto principal é não ter medo de experimentar forças diferentes calculadas de maneiras diferentes, porque agora você tem um simulador real de gráficos bidimensionais, tente diferentes tipos de forças!

Deixei todo o código e links necessários no meu site porque não há mais espaço. Na minha aplicação simples, implementei o algoritmo da dinâmica de um mundo bidimensional e também adicionei objetos presos por uma mola; eles giram em torno de seu eixo e, às vezes, até colidem com paredes, giram. Mas vou falar sobre isso outra vez. Siga o link para obter mais literatura e um aplicativo simples para Windows 32 e Macintosh.

Muito raramente, Chris Hecker experimenta o efeito do momento de inércia, mas geralmente passa rapidamente. As forças podem ser aplicadas a checker@bix.com.

Notas do tradutor: um trocadilho é apresentado aqui, o tópico do artigo e seu conteúdo são exibidos.

PS Feedback é bem-vindo. Seus comentários podem melhorar a qualidade do trabalho. Obrigada

PPS O autor da tradução agradece especialmente aos usuários de Berez e Vasily Tereshkov pela edição da tradução. Obrigada