Matrizes de antenas adaptativas: como funciona? (Básico)

Bom dia

Nos últimos anos, dediquei-me à pesquisa e criação de vários algoritmos para processamento espacial de sinais em arranjos de antenas adaptáveis, e continuo fazendo isso como parte do meu trabalho no momento. Aqui eu gostaria de compartilhar o conhecimento e as fichas que descobri. Espero que seja útil para pessoas que estão começando a estudar essa área de processamento de sinais ou apenas interessadas.

O que é um conjunto de antenas adaptáveis?

Um conjunto de antenas é um conjunto de elementos de antenas, dispostos de alguma forma no espaço. Para simplificar a estrutura do conjunto de antenas adaptativas, que consideraremos, pode ser representada da seguinte forma:


Matrizes de antenas adaptativas são freqüentemente chamadas de "antenas inteligentes" (antenas inteligentes ). O conjunto de antenas “inteligentes” é feito pela unidade de processamento de sinal espacial e pelos algoritmos implementados nele. Esses algoritmos analisam o sinal recebido e formam um conjunto de pesos$$ $ inline $ w_1 ... w_N $ inline $ que determinam a amplitude e a fase inicial do sinal para cada um dos elementos. A distribuição amplitude-fase dada determina o padrão de diretividade de toda a rede como um todo. A capacidade de sintetizar o padrão de radiação da forma requerida e alterá-lo durante o processamento do sinal é uma das principais características dos arranjos de antenas adaptáveis, o que permite resolver uma ampla gama de problemas . Mas as primeiras coisas primeiro.

Como é formado o padrão de radiação?

Um padrão de radiação caracteriza a potência de um sinal irradiado em uma determinada direção. Para simplificar, colocamos os elementos da rede isotrópicos, ou seja, para cada um deles, a potência do sinal emitido não depende da direção. A amplificação ou atenuação da potência irradiada pelo conjunto em uma determinada direção é obtida devido à interferência das ondas eletromagnéticas emitidas por vários elementos do conjunto de antenas. Um padrão de interferência estável para EMW é possível apenas se eles forem coerentes , ou seja, a diferença de fase dos sinais não deve mudar com o tempo. No caso ideal, cada um dos elementos da matriz da antena deve emitir um sinal harmônico na mesma frequência portadora$$ $ inline $ f_ {0} $ inline $ . No entanto, na prática, é necessário trabalhar com sinais de banda estreita com um espectro de largura finita$$ $ inline $ \ Delta f << f_ {0} $ inline $ .
Deixe todos os elementos AR emitir o mesmo sinal com amplitude complexa$$ $ inline $ x_n (t) = u (t) $ inline $ . Então, no receptor remoto , o sinal recebido do enésimo elemento pode ser representado de uma forma analítica :

$$$$ exibir $$ a_n (t) = u (t- \ tau_n) e ^ {i2 \ pi f_0 (t- \ tau_n)} $$ exibir $$

onde$$ $ inline $ \ tau_n $ inline $ - atraso na propagação do sinal do elemento da antena até o ponto de recepção.
Esse sinal é "quase harmônico" e, para satisfazer a condição de coerência, é necessário que o atraso máximo na propagação de ondas eletromagnéticas entre dois elementos seja muito menor que o tempo característico do envelope do sinal$$ $ inline $ T $ inline $ , ou seja,$$ $ inline $ u (t- \ tau_n) ≈ u (t- \ tau_m) $ inline $ . Assim, a condição para a coerência de um sinal de banda estreita pode ser escrita da seguinte maneira:

$$$$ display $$ T≈ \ frac {1} {\ Delta f} >> \ frac {D_ {max}} {c} = max (\ tau_k- \ tau_m) $$ display $$

onde$$ $ inline $ D_ {max} $ inline $ - a distância máxima entre os elementos da AR , e$$ $ inline $ com $ inline $ É a velocidade da luz.

Ao receber um sinal, a soma coerente é realizada digitalmente na unidade de processamento espacial. Nesse caso, o valor complexo do sinal digital na saída deste bloco é determinado pela expressão:

$$$$ display $$ y = \ sum_ {n = 1} ^ Nw_n ^ * x_n $$ display $$

É mais conveniente apresentar a última expressão na forma de um produto escalar de vetores complexos N-dimensionais na forma de matriz:

$$$$ display $$ y = (\ textbf {w}, \ textbf {x}) = \ textbf {w} ^ H \ textbf {x} $$ display $$

onde w e x são vetores de coluna e$$ $ inline $ (.) ^ H $ inline $ - operação de emparelhamento hermitiano .

A representação vetorial de sinais é um dos elementos básicos ao trabalhar com matrizes de antenas, porque muitas vezes evita cálculos matemáticos pesados. Além disso, a identificação de um sinal recebido em um determinado momento com um vetor geralmente nos permite abstrair de um sistema físico real e entender o que exatamente acontece do ponto de vista da geometria.

Para calcular o padrão de diretividade do conjunto de antenas, é necessário "mentalmente e consistentemente" executar nele um conjunto de ondas planas de todas as direções possíveis. Nesse caso, os valores dos elementos do vetor x podem ser representados da seguinte maneira:

$$$$ display $$ x_n = s_n = \ exp \ {- i (\ textbf {k} (\ phi, \ theta), \ textbf {r} _n) \} $$ display $$

onde k é o vetor de onda$$ $ inline $ \ phi $ inline $ e$$ $ inline $ \ theta $ inline $ - ângulo azimutal e ângulo de elevação que caracterizam a direção de chegada de uma onda plana,$$ $ inline $ \ textbf {r} _n $ inline $ - coordenada do elemento da antena,$$ $ inline $ s_n $ inline $ - um elemento do vetor de fase s de uma onda plana com o vetor de onda k (na literatura inglesa, o vetor de fase é chamado vetor de orientação). A dependência do quadrado da amplitude de y em$$ $ inline $ \ phi $ inline $ e$$ $ inline $ \ theta $ inline $ determina o padrão de diretividade da matriz de antenas na recepção para um determinado vetor de coeficientes de peso w .

Recursos do conjunto de antenas

É conveniente estudar as propriedades gerais do padrão de radiação do conjunto de antenas em um conjunto de antenas equidistantes lineares em um plano horizontal (isto é, o padrão de feixe depende apenas do ângulo azimutal$$ $ inline $ \ phi $ inline $ ) É conveniente de dois pontos de vista: cálculos analíticos e apresentação visual.

Calculamos o DN para um vetor de peso unitário ($$ $ inline $ w_n = 1, n = 1 ... N $ inline $ ), seguindo a abordagem descrita acima .


Como resultado, obtemos:

$$$$ display $$ F (\ phi) = | y | ^ 2 = \ frac {\ sin ^ 2 (\ pi \ frac {Nd} {\ lambda} \ sin \ phi)} {\ sin ^ 2 (\ pi \ frac {d} {\ lambda} \ sin \ phi)} $$ exibir $$

Frequência do padrão de radiação

O padrão de radiação resultante do conjunto de antenas é uma função periódica do seno do ângulo. Isso significa que, para certos valores da razão d / λ , possui máximos de difração (adicionais).
Padrão de antena não normalizado para N = 5
Padrão de radiação normalizado do conjunto de antenas para N = 5 no sistema de coordenadas polares

A posição dos "difracionistas" pode ser vista diretamente da fórmula do NAM. No entanto, tentaremos entender de onde eles vêm física e geometricamente (no espaço N-dimensional).

Os elementos do vetor de fase s são expoentes complexos$$ $ inline $ e ^ {i \ Psi n} $ inline $ cujos valores são determinados pelo valor do ângulo generalizado$$ $ inline $ \ Psi = 2 \ pi \ frac {d} {\ lambda} \ sin \ phi $ inline $ . Se houver dois ângulos generalizados correspondentes a diferentes direções de chegada de uma onda plana, para os quais$$ $ inline $ \ Psi_1 = \ Psi_2 + 2 \ pi m $ inline $ , isso significa duas coisas:

• Fisicamente: as frentes de ondas planas provenientes dessas direções induzem distribuições idênticas de fase de amplitude das ondas eletromagnéticas nos elementos do conjunto de antenas.
• Geometricamente: vetores de fases para essas duas direções coincidem.

As direções de chegada das ondas conectadas de maneira semelhante são equivalentes do ponto de vista do conjunto de antenas e não são distinguíveis entre si.

Como determinar a região dos ângulos em que apenas um máximo principal do MD está sempre? Faremos isso nas proximidades do azimute zero pelas seguintes razões: a mudança de fase entre dois elementos adjacentes deve estar no intervalo entre$$ $ inline $ - \ pi $ inline $ antes$$ $ inline $ \ pi $ inline $ .

$$exibição $$ $$ - \ pi <2 \ pi \ frac {d} {\ lambda} \ sin \ phi <\ pi $$ exibição $$

Resolvendo essa desigualdade, obtemos a condição na região de singularidade em um bairro zero:

$$$$ exibir $$ | \ sin \ phi | <\ frac {\ lambda} {2d} $$ exibir $$

Pode-se observar que o tamanho da região de singularidade em ângulo depende da razão d / λ . Se d = 0,5 λ , então cada direção de chegada do sinal é "individual", e a região de singularidade cobre toda a gama de ângulos. Se d = 2,0 λ , as direções 0, ± 30, ± 90 são equivalentes. Os lobos de difração aparecem no padrão de radiação.

Normalmente, os lobos de difração tendem a suprimir usando elementos de antena direcionais. Nesse caso, o padrão completo de radiação do conjunto de antenas é o produto do padrão de um elemento e o conjunto de elementos isotrópicos. Os parâmetros DN de um elemento geralmente são selecionados com base na condição na região de exclusividade do conjunto de antenas.

A largura do lobo principal

A fórmula de engenharia para estimar a largura do lóbulo principal do sistema de antena é amplamente conhecida :$$ $ inline $ \ Delta \ phi \ frac {\ lambda} {D} $ inline $ onde D é o tamanho característico da antena. A fórmula é usada para vários tipos de antenas, incluindo SLR. Mostramos que também é válido para matrizes de antenas.

Determinamos a largura do lobo principal pelos primeiros zeros do MD nas proximidades do máximo principal. Numerador de expressão para$$ $ inline $ F (\ phi) $ inline $ desaparece em$$ $ inline $ \ sin \ phi = m \ frac {\ lambda} {dN} $ inline $ . Os primeiros zeros correspondem a m = ± 1. Assumindo$$ $ inline $ \ frac {\ lambda} {dN} << 1 $ inline $ nós temos$$ $ inline $ \ Delta \ phi = 2 \ frac {\ lambda} {dN} $ inline $ .

Normalmente, a largura do feixe de diretividade AR é determinada pelo nível de meia potência (-3 dB). Nesse caso, use a expressão:

$$exibição $$ $$ \ Delta \ phi≈0,88 \ frac {\ lambda} {dN} exibição $$ $$ $$

A largura do lóbulo principal pode ser controlada através da definição de diferentes valores das amplitudes para os coeficientes de peso do conjunto de antenas. Considere três distribuições:

• Distribuição uniforme da amplitude (pesos 1):$$ $ inline $ w_n = 1 $ inline $ .
• Valores de amplitude caindo para as bordas da rede (pesos 2):$$ $ inline $ w_n = 0,5 + 0,3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ inline $
• Valores de amplitude aumentando para as bordas da grade (pesos 3):$$ $ inline $ w_n = 0.5-0.3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ inline $

A figura mostra os padrões de radiação normalizada resultantes em uma escala logarítmica:
As seguintes tendências podem ser rastreadas a partir da figura: a distribuição das amplitudes dos coeficientes de peso diminuindo em direção às bordas da treliça leva a um alargamento do lobo principal do MD, mas a uma diminuição no nível dos lobos laterais. As amplitudes aumentando em direção às bordas da matriz de antenas, pelo contrário, levam a um estreitamento do lobo principal e a um aumento no nível dos lados. É conveniente considerar a limitação de casos aqui:

1. As amplitudes dos coeficientes de ponderação de todos os elementos, exceto os extremos, são iguais a zero. Os pesos para elementos extremos são iguais à unidade. Nesse caso, a rede torna-se equivalente a um AR de dois elementos com um período de D = (N-1) d . Não é difícil estimar, de acordo com a fórmula acima, a largura da pétala principal. Nesse caso, as laterais se transformarão em máximos de difração e se alinharão com o máximo principal.
2. O peso do elemento central é igual a um e o restante a zero. Nesse caso, basicamente temos uma antena com um padrão de radiação isotrópica.

A direção do máximo principal

Então, vimos como você pode ajustar a largura do lóbulo principal do AP AR . Agora vamos ver como direcionar a direção. Lembre-se da expressão vetorial para o sinal recebido. Suponha que queremos que o padrão máximo de radiação olhe em uma determinada direção$$ $ inline $ \ phi_0 $ inline $ . Isso significa que a potência máxima deve ser tomada nessa direção. O vetor de fase corresponde a essa direção$$ $ inline $ \ textbf {s} (\ phi_0) $ inline $ no espaço vetorial dimensional N , e a potência recebida é definida como o quadrado do produto escalar desse vetor de fase pelo vetor dos coeficientes de peso w . O produto escalar de dois vetores é máximo quando eles são colineares , ou seja,$$ $ inline $ \ textbf {w} = \ beta \ textbf {s} (\ phi_0) $ inline $ , onde β é algum fator de normalização. Assim, se escolhermos um vetor de peso igual ao vetor de fase para a direção desejada, giraremos o padrão máximo de radiação.

Considere os seguintes pesos como exemplo:$$ $ inline $ \ textbf {w} = \ textbf {s} (10 °) $ inline $

$$$$ display $$ w_n = \ exp \ {i2 \ pi \ frac {d} {\ lambda} (n-1) \ sin (10 \ pi / 180) \} $$ display $$

Como resultado, obtemos um padrão de radiação com o máximo principal na direção de 10 °.

Agora aplicamos os mesmos pesos, mas não para recepção de sinal, mas para transmissão. Aqui vale a pena considerar que, ao transmitir um sinal, a direção do vetor de onda é invertida. Isso significa que os elementos do vetor de fase para recepção e transmissão diferem no sinal no expoente, ou seja, interconectados por conjugação complexa. Como resultado, obtemos o máximo do padrão de radiação na direção de -10 °, que não coincide com o máximo do sinal de recebimento nos mesmos coeficientes de peso.Para corrigir a situação, é necessário aplicar conjugação complexa também aos coeficientes de peso.

A característica descrita da formação dos feixes para recepção e transmissão deve sempre ser lembrada ao trabalhar com conjuntos de antenas.

Vamos brincar com o padrão de radiação

Poucos altos

Colocamos o problema para formar dois máximos principais do padrão de radiação na direção: -5 ° e 10 °. Para fazer isso, escolhemos a soma ponderada dos vetores de fases para as direções correspondentes como o vetor de peso.

$$$$ display $$ \ textbf {w} = \ beta \ textbf {s} (10 °) + (1- \ beta) \ textbf {s} (- 5 °) $$ display $$

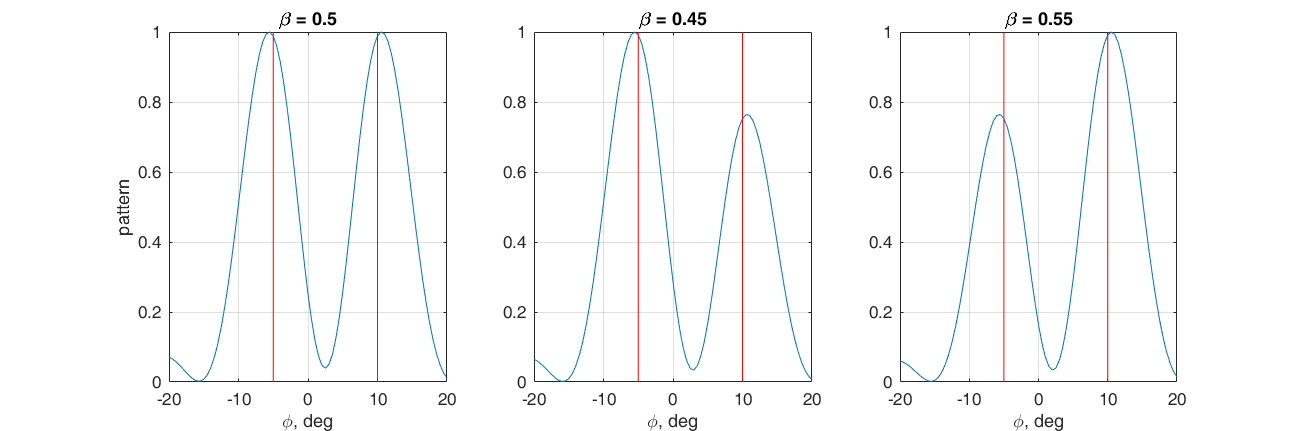
Ajustando o coeficiente β , a relação entre os lobos principais pode ser ajustada. Aqui, novamente, é conveniente observar o que está acontecendo no espaço vetorial. Se β for maior que 0,5, o vetor de pesos estará mais próximo de s (10 °), caso contrário, de s (-5 °). Quanto mais próximo o vetor de peso de um dos fasores, maior o produto escalar correspondente e, portanto, a magnitude do máximo correspondente do ND .

No entanto, vale a pena considerar que ambas as pétalas principais têm uma largura finita e, se quisermos sintonizar em duas direções próximas, essas pétalas se fundirão em uma, orientada para alguma direção intermediária.

Um máximo e zero

Agora vamos tentar ajustar o padrão máximo de radiação para a direção$$ $ inline $ \ phi_1 = 10 ° $ inline $ e simultaneamente suprimir o sinal vindo da direção$$ $ inline $ \ phi_2 = -5 ° $ inline $ . Para isso, é necessário definir o zero para o ângulo correspondente. Você pode fazer isso da seguinte maneira:

$$$$ display $$ \ textbf {w} = \ textbf {s} _1- \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {N} \ textbf {s} _2 $$ display $$

onde$$ $ inline $ \ textbf {s} _1 = \ textbf {s} (10 °) $ inline $ e$$ $ inline $ \ textbf {s} _2 = \ textbf {s} (- 5 °) $ inline $ .

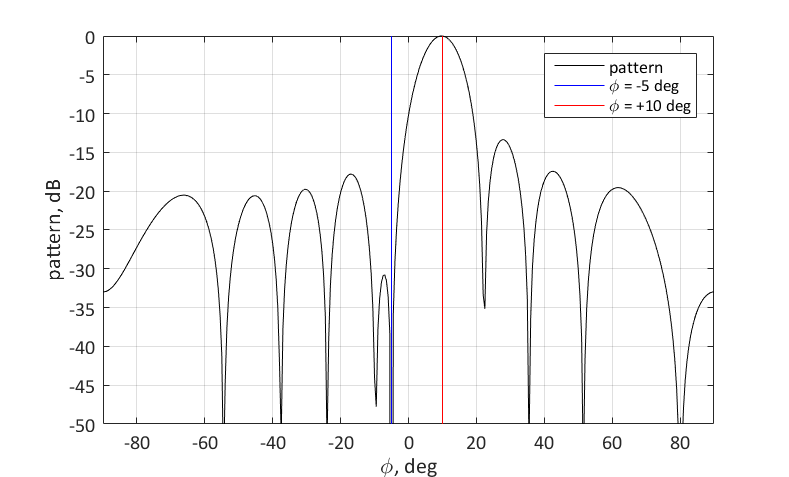
O significado geométrico da escolha do vetor de peso é o seguinte. Queremos que esse vetor w tenha uma projeção máxima em$$ $ inline $ \ textbf {s} _1 $ inline $ e era ortogonal ao vetor$$ $ inline $ \ textbf {s} _2 $ inline $ . Vetor$$ $ inline $ \ textbf {s} _1 $ inline $ pode ser representado como dois termos: vetor colinear$$ $ inline $ \ textbf {s} _2 $ inline $ e vetor ortogonal$$ $ inline $ \ textbf {s} _2 $ inline $ . Para satisfazer a afirmação do problema, é necessário escolher o segundo componente como o vetor dos coeficientes de peso w . O componente colinear pode ser calculado projetando um vetor$$ $ inline $ \ textbf {s} _1 $ inline $ para vetor normalizado$$ $ inline $ \ frac {\ textbf {s} _2} {\ sqrt {N}} $ inline $ usando um produto escalar.

$$$$ display $$ \ textbf {s} _ {1 ||} = \ frac {\ textbf {s} _2} {\ sqrt {N}} \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {\ sqrt {N}} $$ exibir $$

Assim, subtraindo do vetor inicial de fases$$ $ inline $ \ textbf {s} _1 $ inline $ seu componente colinear, obtemos o vetor de peso desejado.

Algumas notas adicionais

1. Em todos os lugares acima, omiti a questão de normalizar o vetor de peso, ou seja, seu comprimento. Portanto, a normalização do vetor de peso não afeta as características do padrão de radiação do conjunto de antenas: a direção da máxima principal, a largura do lóbulo principal etc. Também pode ser mostrado que essa normalização não afeta o SNR na saída do bloco de processamento espacial. A este respeito, ao considerar algoritmos de processamento de sinal espacial, geralmente aceito uma normalização unitária do vetor de peso, ou seja,$$ $ inline $ \ textbf {w} ^ H \ textbf {w} = 1 $ inline $
2. As possibilidades para a formação do fundo da matriz de antenas são determinadas pelo número de elementos N. Quanto mais elementos, maiores as possibilidades. Quanto mais graus de liberdade na implementação do processamento de peso espacial, mais opções de como "torcer" o vetor de peso no espaço N-dimensional.
3. Ao receber o padrão de feixe da antena , o conjunto de antenas não existe fisicamente e tudo isso existe apenas na "imaginação" da unidade de computação que processa o sinal. Isso significa que, ao mesmo tempo, é possível sintetizar vários MDs e processar de forma independente os sinais que chegam de direções diferentes. No caso da transmissão, tudo é um pouco mais complicado, mas também é possível sintetizar vários MDs para transmitir vários fluxos de dados. Essa tecnologia em sistemas de comunicação é chamada MIMO .
4. Usando o código matlab fornecido, você pode jogar com o NAM
   
   Código

   % antenna array settings N = 10; % number of elements d = 0.5; % period of antenna array wLength = 1; % wavelength mode = 'receiver'; % receiver or transmitter % weights of antenna array w = ones(N,1); % w = 0.5 + 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = 0.5 - 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+10/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+3/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-3/180*pi)*(0:N-1)).'; % s1 = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % s2 = exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % w = s1 - (1/N)*s2*s2'*s1; % w = s1; % normalize weights w = w./sqrt(sum(abs(w).^2)); % set of angle values to calculate pattern angGrid_deg = (-90:0.5:90); % convert degree to radian angGrid = angGrid_deg * pi / 180; % calculate set of steerage vectors for angle grid switch (mode) case 'receiver' s = exp(2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); case 'transmitter' s = exp(-2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); end % calculate pattern y = (abs(w'*s)).^2; %linear scale plot(angGrid_deg,y/max(y)); grid on; xlim([-90 90]); % log scale % plot(angGrid_deg,10*log10(y/max(y))); % grid on; % xlim([-90 90]); 

   
   

Quais tarefas podem ser resolvidas com a ajuda de um conjunto de antenas adaptáveis?

Obrigado pela atenção.