Esta é uma tradução de um artigo de Eliezer Yudkovsky de um ciclo científico popular dedicado à interpretação multivariada da mecânica quântica. O início do ciclo foi traduzido para um hub , mas o tradutor aparentemente se cansou. Pode ser entendido - o material é muito volumoso. Yudkovsky gosta de espalhar o pensamento na árvore. Por outro lado, o material é realmente complexo, e a repetição da mesma coisa em palavras diferentes permite que a imagem na cabeça de um leitor despreparado se mantenha, pelo menos de alguma maneira. Não me comprometerei a continuar a tradução de todo o ciclo, mas tentarei traduzir alguns dos artigos mais importantes.

Vou pular artigos da série sobre espaços de estados ( clássicos e quânticos ) - o conceito é usado muito onde e deve ser familiar para um leitor tecnicamente treinado. E também pule as integrais do caminho de Feynman - elas podem ser encontradas na excelente fonte científica popular.

Mas o próximo post responde a uma pergunta importante. Se o mundo "real" no nível fundamental é quântico, onde tudo está confuso e tudo afeta um ao outro, de onde vêm os sistemas clássicos? Por que vemos fenômenos quânticos “naturais” tão raramente na vida comum? Isso é o que o autor chama de "alucinação clássica". Por que, por exemplo, os criadores de computadores quânticos precisam fazer esforços tremendos para manter o sistema em um estado emaranhado "natural"?

Isenção de responsabilidade: eu não sou um físico profissional nem um tradutor profissional (assim como o autor do original).

Decoherence

Para entender um processo quântico chamado “decoerência”, primeiro você precisa entender como um estado especial de independência quântica é destruído - isto é, como exatamente um sistema quântico passa de um estado de independência para um estado de emaranhamento.

A independência quântica, como lembramos , é um estado especial, "retangular", de distribuição de amplitude que é bem fatorado. Ou seja, pode ser representado como o produto das distribuições das partes constituintes do sistema, que para nós parecem “partículas separadas”.

Os turistas tímidos que visitam nosso mundo quântico às vezes sentem falta de uma distribuição "retangular" para alguma conexão misteriosa especial entre partículas. Daí o infeliz termo "entrelaçamento quântico". De fato, qualquer evolução de um sistema quântico geralmente gera emaranhamento da independência (e não vice-versa), transformando distribuições retangulares em não retangulares. A independência é rara e muito fácil de destruir.

Para entender melhor exatamente quais processos físicos levam ao emaranhamento, começamos com o sistema clássico. A figura mostra um sistema de uma bola leve carregada positivamente na pista superior e uma bola pesada carregada negativamente na pista inferior. Inicialmente, duas bolas estão distantes e quase não interagem. Então abaixamos o caminho superior, juntando as bolas para que elas comecem a se atrair (cargas opostas são atraídas). E uma bola leve rola até uma pesada (e uma bola pesada rola um pouco até uma leve, assim como uma maçã que cai atrai a Terra levemente para si).

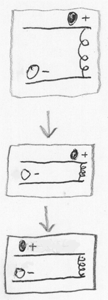
Agora, vejamos esse sistema como um sistema quântico, do ponto de vista das integrais do caminho de Feynman . Ou seja, representamos a evolução do sistema como a soma de todas as trajetórias possíveis do estado inicial no espaço de configuração. Suponha que duas bolas sejam inicialmente independentes quânticas, sua distribuição conjunta de amplitudes pode ser representada como o produto de "distribuição para a bola inferior" e "distribuição para a bola superior".

Além disso, deixe a amplitude da bola inferior no início consistir em três partes (que, do ponto de vista das integrais de Feynman, podem ser consideradas como três estados iniciais). Quando abaixamos a pista superior, a bola superior deve ser puxada para a pista inferior. Mas se a amplitude conjunta da bola inferior consistir em várias partes, no final obteremos uma distribuição conjunta composta por várias partes, cada uma das quais descreve a nova posição das bolas.

Estou tentando o meu melhor para evitar formulações como “a bola inferior pode estar em um dos três lugares” ou “em cada caso possível, a bola superior é atraída para a posição correspondente da menor”. Embora você provavelmente ainda imagine tudo dessa maneira. No final, eu próprio ilustrei isso. Desenhei três possíveis posições iniciais e três possíveis resultados. O que fazer, o cérebro humano geralmente imagina as integrais de Feynman. Mas isso não significa que existem três estados possíveis do universo . Este é apenas um truque para visualizar o caminho integral. Todos os três componentes da amplitude existem em nosso universo, todos os três são igualmente reais , mas nem um pouco possíveis ou prováveis .

Agora imagine que, a princípio, a amplitude da bola inferior seja "borrada" por toda a pista. A amplitude da bola superior ainda está concentrada em um só lugar. Em seguida, a distribuição da junta será inicialmente na forma de um retângulo alongado e depois se transformará em uma diagonal.

No eixo X, aqui está a posição da bola superior, no eixo Y - a parte inferior. Começamos com uma bola superior precisamente localizada e uma bola inferior "borrada" e terminamos com uma distribuição interdependente quando ambas as coordenadas estão borradas, mas iguais umas às outras (simplificadas). Ou seja, a distribuição inicialmente fatorável se transformou em um "sistema confuso" - não se decompõe mais em dois fatores independentes.

(Aviso importante:

Observe que, na figura acima, o desenvolvimento do sistema obedece à segunda lei da termodinâmica , também conhecida como teorema de Liouville. Quando o sistema muda, o "tamanho da nuvem" é preservado, ou seja, o volume total da amplitude, ou mais simplesmente, o tamanho da área cinza no gráfico . Se no início da figura havia um enorme quadrado cinza claro (quando as duas partículas estão fortemente manchadas no espaço), então, de acordo com a segunda lei da termodinâmica, ele não poderia se transformar em uma diagonal cinza escura. Para entrar em um estado de emaranhamento, o sistema deve inicialmente ter baixa entropia, e essa entropia não deve aumentar muito no processo.

Deixe-me lembrá-lo de que informações mútuas são entropia com o sinal oposto . Amplitudes quânticas não são inteiramente informações , mas o princípio é o mesmo. A amplitude inicial deve ser concentrada o suficiente para produzir uma linha diagonal compacta, em vez de uma grande nuvem rarefeita. Se imaginarmos que a distribuição de amplitude tem "entropia quântica", a entropia do sistema emaranhado deve ser relativamente baixa)

Finalmente, estamos prontos para falar sobre decoerência.

O sistema na figura é bastante complicado. Pode ser descrito algo como isto: "existem duas partículas, e ambas podem estar aqui ou ali ". Sim, eu o formulei como se houvesse dois estados possíveis, e não uma distribuição fisicamente real da amplitude. Sério, não sei como descrever a física quântica em uma linguagem comum e de maneira normal! Lembre-se da regra geral de que "oportunidade" ou "probabilidade" é uma abreviação de "trecho de distribuição de amplitude fisicamente existente". Então eu posso descrever as amplitudes muito mais curtas usando os termos das incertezas. Mas lembre-se de que isso é apenas uma convenção ! “Uma partícula está aqui ou ali” significa “uma distribuição fisicamente existente da amplitude de duas partes, uma aqui, outra ali”, e não “a partícula está em um dos dois lugares, mas não sabemos qual”.

Então Trabalhar com sistemas complexos é geralmente difícil (para os físicos, é claro, não para o universo). Primeiro, devemos calcular todas as trajetórias possíveis para todas as condições iniciais possíveis (ou seja, levar em consideração todas as trajetórias de amplitude fisicamente existentes na integral de Feynman). Além disso, é necessário levar em consideração a influência dessas trajetórias uma sobre a outra (trajetórias prováveis ​​no sentido estrito não podem interagir - apenas algo realmente existente pode influenciar outra coisa). Por exemplo, nossas duas partículas se encontram com outras 20, interagem de alguma maneira e, como resultado, obtemos várias configurações afetadas por todos os pontos anteriores de todos os estados possíveis.

Observe que o emaranhamento ocorre apenas se seções da amplitude inicial estiverem próximas uma da outra. Para que seus caminhos de desenvolvimento possam se cruzar. Se duas partículas estão aqui ou ali , mas "aqui" e "lá" são separadas por uma distância de dois anos-luz, suas trajetórias adicionais podem se cruzar não antes de um ano depois.

Agora adicione a terceira partícula. A figura mostra um espaço de configuração tridimensional, que se decompõe em subespaços bidimensionais e unidimensionais independentes. Ou seja, duas partículas emaranhadas e uma independente delas.

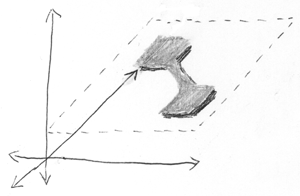
Altura é a terceira partícula, largura e profundidade são duas partículas emaranhadas.

Uma partícula independente está em um determinado local - a distribuição vertical é muito estreita. Duas partículas entrelaçadas estão aqui ou ali (novamente uso termos probabilísticos incorretos, como "específico" e "qualquer um", mas você entende o que quero dizer).

Imagine agora que a terceira partícula reage com as duas emaranhadas de uma maneira que é sensível à sua posição. Por exemplo, a terceira partícula se equilibra em um pico agudo, duas partículas voam, atraem-na e cai de uma maneira ou de outra. Depois disso, a amplitude se parece com isso.

A terceira partícula agora está confusa com as outras duas. E a amplitude agora consiste em duas partes separadas uma da outra . Descrição simplificada: “se duas partículas estavam aqui , a terceira partícula voou aqui . E se eles estavam lá , ela voou para lá . Ou seja, a amplitude tornou-se completamente confusa. Ele não se decompõe mais em subespaços independentes.

Mas agora duas partes de amplitude estão mais afastadas e cada uma consiste em três partículas na região correspondente. Isso aconteceu porque a terceira partícula é sensível à coordenada de outras. Depois de rolar de um pico agudo para um dos dois lados, a distância entre as coordenadas finais é bastante grande.

De fato, rolar para baixo é opcional. Tudo funciona da mesma maneira se você tiver vinte partículas que reagem às duas primeiras e se confundem com elas. A distribuição final no espaço 22-dimensional será semelhante a duas áreas, cada uma das quais corresponde a 22 partículas. E a distância entre essas áreas será enorme. E quanto maior a distância, menor a probabilidade de as áreas no futuro se afetarem.
Isso é decoerência. É a terceira causa de "alucinação clássica", porque as duas áreas começam a se desenvolver independentemente. Isso permite que eles sejam descritos como sistemas não intrincados. Assim que os consideramos separadamente, a distribuição em cada um deles parece "retangular" e independentemente em três coordenadas (tentei mostrar isso na figura acima).

Em um computador quântico, é muito difícil impedir a decoerência. A computação quântica exige que as seções de amplitude permaneçam próximas umas das outras e possam interagir. Mas existem trilhões de outras partículas ao redor que constantemente tentam reagir inadvertidamente com nossos qubits frágeis, destruindo a amplitude precisamente construída.

E você não pode simplesmente pegar e restaurar os destruídos. Para isso, é necessário retornar ao local todas as partículas reagidas, incluindo partículas aleatórias do ambiente (não se esqueça, a amplitude final possui uma distribuição conjunta com elas).

(Parece um processo quase irreversível, certo? É como tentar coletar um ovo quebrado de volta à casca. Na verdade, essa é uma boa analogia.

Por isso, enfatizei anteriormente que o processo de entrelaçamento começa com baixa entropia. A descoerência é irreversível porque é essencialmente um processo termodinâmico.

Um dos princípios físicos fundamentais afirma que você pode "reverter o filme" sem violar as leis fundamentais. Se você filmar um ovo caindo no chão e rolá-lo para trás, para que o ovo quebrado voe do chão, juntando-se novamente em uma casca lisa, você não verá nenhuma lei física violada. Todas as moléculas estarão simplesmente no lugar certo, na hora certa, e o ovo ricocheteará no chão, sãos e salvos. Isso não é impossível, apenas extremamente improvável.

O mesmo se aplica à amplitude dividida em partes remotas, retornando inesperadamente a um estado coerente - isso é teoricamente possível. Mas praticamente não há chance de que as peças que foram inicialmente desconectadas sejam repentinamente simultaneamente uma da outra. O processo inverso é muito mais provável.

De fato, além de rolar o filme para trás, você também precisa reverter as cargas de todas as partículas, bem como trocar a esquerda e a direita (ou uma das outras duas dimensões), transformando o universo em uma imagem espelhada. Essa regra é conhecida como "invariância de CPT" das palavras Carga, Paridade e Tempo.

Muito provavelmente, a invariância da CPT é um dos princípios mais básicos do funcionamento do universo. Para os físicos, as tentativas de quebrá-lo parecem quase tão absurdas quanto tentar arremessar uma bola mais rápido que a velocidade da luz. Tanto quanto eu sei, a invariância CPT é necessária para a consistência da Teoria Quântica de Campos.

Portanto, a decoerência parece apenas um processo unidirecional, mas na verdade sua irreversibilidade é termodinâmica, não fundamental. E isso é muito importante, porque daí resulta que a física quântica observa a invariância da CPT.

Até onde sabemos, absolutamente todos os processos unidirecionais da natureza são uma conseqüência da segunda lei da termodinâmica, e não a assimetria fundamental do tempo.)

Para resumir. A decoerência é um processo termodinâmico de um emaranhado quântico cada vez maior, que é surpreendentemente disfarçado como um processo de destruição do próprio emaranhado. Áreas descoerentes não interagem entre si e cada uma delas se torna menos confusa . Descoerência é a terceira razão para "alucinação clássica". Permite que os físicos considerem cada campo como independente, sem levar em conta a pouca probabilidade de sua interação. Além disso, cada área individual fica mais fácil de entender. Isso é muito útil se você quiser resolver problemas em termos de física clássica simples. E é muito inapropriado se você quiser fatorar um número de um milhão de dígitos antes que o sol se ponha.