Olá amigos. O curso
Algoritmos para desenvolvedores começa amanhã e ainda temos uma tradução não publicada. Na verdade, corrigimos e compartilhamos material com você. Vamos lá
A Transformada Rápida de Fourier (FFT) é um dos mais importantes algoritmos de processamento de sinais e análise de dados. Eu o usei por anos sem conhecimento formal em ciência da computação. Mas nesta semana me ocorreu que nunca me perguntei como a FFT calcula a transformada discreta de Fourier tão rapidamente. Afastei a poeira de um livro antigo sobre algoritmos, abri-o e li com prazer o truque computacional enganosamente simples que J.V. Cooley e John Tukey descreveram em seu clássico
trabalho de 1965 sobre esse tópico.
O objetivo deste post é mergulhar no algoritmo Cooley-Tukey FFT, explicando as simetrias que levam a ele e mostrar algumas implementações simples do Python que aplicam a teoria na prática. Espero que este estudo forneça a especialistas em análise de dados, como eu, uma imagem mais completa do que está acontecendo sob o capô dos algoritmos que usamos.
Transformação discreta de FourierFFT é rápido
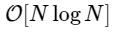
um algoritmo para calcular a transformada discreta de Fourier (DFT), calculada diretamente para
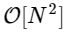
. A DFT, como a versão contínua mais familiar da transformação de Fourier, tem uma forma direta e inversa, que são definidas da seguinte forma:
Transformada direta de Fourier discreta (DFT):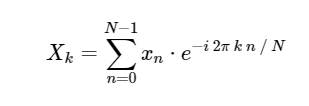
Transformada de Fourier Discreta Inversa (ODPF):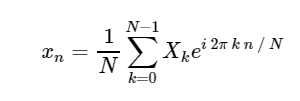
A conversão de
xn → Xk é uma conversão do espaço de configuração para o espaço de frequência e pode ser muito útil para estudar o espectro de potência do sinal e para converter determinadas tarefas para um cálculo mais eficiente. Você pode encontrar alguns exemplos disso em ação no
capítulo 10 do nosso futuro livro sobre astronomia e estatística, onde também pode encontrar imagens e código-fonte em Python. Para um exemplo de uso da FFT para simplificar a integração de equações diferenciais complicadas, consulte meu post
"Resolvendo a equação de Schrödinger em Python" .
Devido à importância da FFT (daqui em diante, a FFT equivalente - Fast Fourier Transform pode ser usada) em muitas áreas do Python contém muitas ferramentas e shells padrão para o cálculo. Tanto o NumPy quanto o SciPy possuem shells da biblioteca FFTPACK extremamente testada, que são encontrados nos
scipy.fftpack e
scipy.fftpack respectivamente. A FFT mais rápida que conheço está no pacote
FFTW , que também está disponível no Python através do pacote
PyFFTW .
No momento, no entanto, vamos deixar essas implementações de lado e imaginar como podemos calcular a FFT no Python do zero.
Cálculo de transformada discreta de FourierPor simplicidade, trataremos apenas da conversão direta, pois a transformação inversa pode ser implementada de maneira muito semelhante. Observando a expressão acima da DFT, vemos que isso nada mais é do que uma operação linear direta: multiplicar a matriz por um vetor
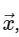
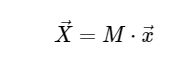
com matriz M dada
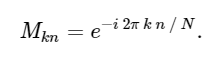
Com isso em mente, podemos calcular a DFT usando uma multiplicação de matrizes simples da seguinte maneira:
Em [1]:
import numpy as np def DFT_slow(x): """Compute the discrete Fourier Transform of the 1D array x""" x = np.asarray(x, dtype=float) N = x.shape[0] n = np.arange(N) k = n.reshape((N, 1)) M = np.exp(-2j * np.pi * k * n / N) return np.dot(M, x)
Podemos verificar o resultado comparando-o com a função FFT incorporada ao numpy:
Em [2]:
x = np.random.random(1024) np.allclose(DFT_slow(x), np.fft.fft(x))
0ut [2]:
TrueApenas para confirmar a lentidão do nosso algoritmo, podemos comparar o tempo de execução dessas duas abordagens:
Em [3]:
%timeit DFT_slow(x) %timeit np.fft.fft(x)
10 loops, best of 3: 75.4 ms per loop 10000 loops, best of 3: 25.5 µs per loop
Somos mais de 1000 vezes mais lentos, o que é esperado para uma implementação tão simplificada. Mas isso não é o pior. Para um vetor de entrada de comprimento N, o algoritmo FFT é escalado como
enquanto nosso algoritmo lento escala como
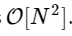
. Isso significa que para
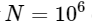
elementos, esperamos que a FFT seja concluída em cerca de 50 ms, enquanto nosso algoritmo lento levará cerca de 20 horas!
Então, como a FFT consegue tal aceleração? A resposta é usar simetria.
Simetrias na transformada discreta de FourierUma das ferramentas mais importantes na construção de algoritmos é o uso de simetrias de tarefas. Se você puder mostrar analiticamente que uma parte do problema está simplesmente relacionada à outra, poderá calcular o sub-resultado apenas uma vez e salvar esse custo computacional. Cooley e Tukey usaram exatamente essa abordagem para obter a FFT.
Começamos com a questão do significado
. De nossa expressão acima:
onde usamos a identidade exp [2π in] = 1, que vale para qualquer número inteiro n.
A última linha mostra bem a propriedade de simetria da DFT:
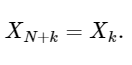
Uma extensão simples
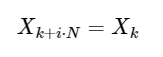
para qualquer número inteiro i. Como veremos abaixo, essa simetria pode ser usada para calcular a DFT muito mais rapidamente.
DFT em FFT: usando simetriaCooley e Tukey mostraram que os cálculos da FFT podem ser divididos em duas partes menores. A partir da definição de DFT, temos:
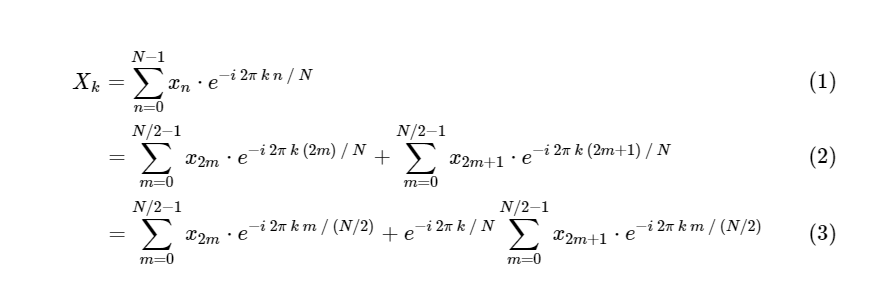
Dividimos uma transformação discreta de Fourier em dois termos, que são muito semelhantes a transformações discretas menores de Fourier, uma para valores com um número ímpar e outra para valores com um número par. No entanto, até agora não salvamos nenhum ciclo computacional. Cada termo consiste em (N / 2) ∗ N cálculos, total
.
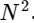
O truque é usar simetria em cada uma dessas condições. Como o intervalo de k é 0≤k <N e o intervalo de n é 0≤n <M≡N / 2, vemos nas propriedades de simetria acima que precisamos executar apenas metade dos cálculos para cada subtarefa. Nosso cálculo
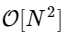
tornou-se
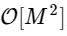
onde M é duas vezes menor que N.
Mas não há razão para insistir nisso: enquanto nossas transformadas de Fourier menores tiverem um M uniforme, podemos reaplicar essa abordagem de divisão e conquista, sempre reduzindo pela metade o custo computacional, até que nossas matrizes sejam pequenas o suficiente para que a estratégia não seja mais beneficiada. No limite assintótico, essa abordagem recursiva escala como O [NlogN].
Esse algoritmo recursivo pode ser implementado muito rapidamente no Python, a partir do nosso código DFT lento, quando o tamanho da subtarefa se torna bem pequeno:
Em [4]:
def FFT(x): """A recursive implementation of the 1D Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if N % 2 > 0: raise ValueError("size of x must be a power of 2") elif N <= 32:
Aqui, faremos uma verificação rápida de que nosso algoritmo fornece o resultado correto:
Em [5]:
x = np.random.random(1024) np.allclose(FFT(x), np.fft.fft(x))
Fora [5]:
TrueCompare este algoritmo com a nossa versão lenta:
-Em [6]:
%timeit DFT_slow(x) %timeit FFT(x) %timeit np.fft.fft(x)
10 loops, best of 3: 77.6 ms per loop 100 loops, best of 3: 4.07 ms per loop 10000 loops, best of 3: 24.7 µs per loop
Nosso cálculo é mais rápido que a versão direta! Além disso, nosso algoritmo recursivo é assintoticamente
: implementamos a rápida transformação de Fourier.
Observe que ainda não estamos próximos da velocidade do algoritmo FFT embutido numpy, e isso deve ser esperado. O algoritmo FFTPACK por trás do
fft numpy é uma implementação do Fortran que recebeu anos de aprimoramento e otimização. Além disso, nossa solução NumPy inclui recursão da pilha Python e alocação de muitas matrizes temporárias, o que aumenta o tempo computacional.
Uma boa estratégia para acelerar o código ao trabalhar com Python / NumPy é vetorizar cálculos repetidos sempre que possível. Podemos fazer isso - no processo, exclua nossas chamadas de função recursivas, o que tornará nossa Python FFT ainda mais eficiente.
Versão numpy vetorizadaObserve que, na implementação recursiva da FFT acima, no nível mais baixo de recursão, realizamos produtos
N / 32 de vetor de matriz idênticos. A eficácia do nosso algoritmo vencerá se calcularmos simultaneamente esses produtos vetor-matriz como um único produto matriz-matriz. Em cada nível de recursão subsequente, também realizamos operações repetitivas que podem ser vetorizadas. O NumPy faz um excelente trabalho com essa operação, e podemos usar esse fato para criar esta versão vetorizada da transformação rápida de Fourier:
Em [7]:
def FFT_vectorized(x): """A vectorized, non-recursive version of the Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if np.log2(N) % 1 > 0: raise ValueError("size of x must be a power of 2")
Embora o algoritmo seja um pouco mais opaco, é simplesmente um rearranjo das operações usadas na versão recursiva, com uma exceção: usamos simetria no cálculo dos coeficientes e construímos apenas metade da matriz. Novamente, confirmamos que nossa função fornece o resultado correto:
Em [8]:
x = np.random.random(1024) np.allclose(FFT_vectorized(x), np.fft.fft(x))
Fora [8]:
TrueÀ medida que nossos algoritmos se tornam muito mais eficientes, podemos usar uma matriz maior para comparar o tempo, deixando
DFT_slow :
Em [9]:
x = np.random.random(1024 * 16) %timeit FFT(x) %timeit FFT_vectorized(x) %timeit np.fft.fft(x)
10 loops, best of 3: 72.8 ms per loop 100 loops, best of 3: 4.11 ms per loop 1000 loops, best of 3: 505 µs per loop
Melhoramos nossa implementação por uma ordem de magnitude! Agora estamos cerca de 10 vezes mais longe do benchmark FFTPACK, usando apenas algumas dezenas de linhas de puro Python + NumPy. Embora isso ainda não seja computacionalmente consistente, em termos de legibilidade, a versão do Python é muito superior ao código fonte do FFTPACK, que você pode ver
aqui .
Então, como o FFTPACK alcança essa última aceleração? Bem, basicamente, é apenas uma questão de contabilidade detalhada. O FFTPACK gasta muito tempo reutilizando todos os cálculos intermediários que podem ser reutilizados. Nossa versão irregular ainda inclui excesso de alocação e cópia de memória; em um idioma de baixo nível, como o Fortran, é mais fácil controlar e minimizar o uso da memória. Além disso, o algoritmo Cooley-Tukey pode ser estendido para usar partições com um tamanho diferente de 2 (o que implementamos aqui é conhecido como Cooley-Tukey Radix FFT da base 2). Outros algoritmos FFT mais complexos também podem ser usados, incluindo abordagens fundamentalmente diferentes baseadas em dados de convolução (consulte, por exemplo, o algoritmo de Blueshtein e o algoritmo Raider). A combinação das extensões e métodos acima pode levar a FFTs muito rápidas, mesmo em matrizes cujo tamanho não é uma potência de duas.
Embora as funções em Python puro sejam provavelmente inúteis na prática, espero que elas forneçam algumas dicas sobre o que está acontecendo no fundo da análise de dados com base na FFT. Como especialistas em dados, podemos lidar com a implementação da “caixa preta” de ferramentas fundamentais criadas por nossos colegas com mais algoritmo, mas acredito firmemente que quanto mais compreensão tivermos sobre os algoritmos de baixo nível que aplicamos aos nossos dados, melhores práticas nós iremos.
Este post foi escrito inteiramente em IPython Notepad. O bloco de notas completo pode ser baixado
aqui ou visualizado estaticamente
aqui .
Muitos podem perceber que o material está longe de ser novo, mas, como nos parece, é bastante relevante. Em geral, escreva se o artigo foi útil. Aguardando seus comentários.