Verificação formal é a verificação de um programa ou algoritmo usando outro.
Este é um dos métodos mais poderosos que permite encontrar todas as vulnerabilidades no programa ou provar que elas não estão lá.
Uma descrição mais detalhada da verificação formal pode ser vista no exemplo de solução do problema de
lobo, cabra e couve no meu artigo anterior.
Neste artigo, passarei da verificação formal de tarefas para programas e descreverei
como convertê-los em sistemas formais de regras automaticamente.
Para isso, escrevi meu análogo de uma máquina virtual, sobre princípios simbólicos.
Ela analisa o código do programa e o converte em um sistema de equações (SMT), que já pode ser resolvido programaticamente.
Como as informações sobre cálculos simbólicos são apresentadas na Internet de maneira fragmentária,
Descreverei brevemente o que é.
Os cálculos de caracteres são uma maneira de executar simultaneamente um programa em uma ampla variedade de dados e são a principal ferramenta para verificação formal de programas.
Por exemplo, podemos definir condições de entrada em que o primeiro argumento pode receber valores positivos, o segundo negativo, o terceiro zero e o argumento de saída, por exemplo, 42.
Cálculos simbólicos em uma execução nos darão a resposta: é possível obter o resultado desejado e um exemplo de um conjunto de tais parâmetros de entrada. Ou a prova de que não existem tais parâmetros.
Além disso, podemos definir os argumentos de entrada em geral o máximo possível e selecionar apenas a saída, por exemplo, a senha do administrador.
Nesse caso, encontraremos todas as vulnerabilidades do programa ou obteremos prova de que a senha do administrador é segura.
Você pode notar que a execução clássica de um programa com dados de entrada específicos é um caso especial de um simbólico.
Portanto, minha VM de personagem também pode funcionar no modo de emulação de uma máquina virtual padrão.
Nos comentários do artigo anterior, você pode encontrar uma crítica justa à verificação formal com uma discussão de suas fraquezas.
Os principais problemas são os seguintes:
- Explosão combinatória, uma vez que a verificação formal repousa em P = NP
- O processamento de chamadas para o sistema de arquivos, redes e outro armazenamento externo é mais difícil de verificar
- Erros na especificação, quando o cliente ou programador concebeu uma coisa, mas não a descreveu com precisão na declaração de trabalho.
Como resultado, o programa será verificado e atenderá às especificações, mas não fará o que os criadores esperavam dele.
Como neste artigo considero principalmente a aplicação da verificação formal na prática, ainda não vou bater na testa contra a parede e vou escolher um sistema em que a complexidade algorítmica e o número de chamadas externas sejam mínimos.
Como os contratos inteligentes atendem a esses requisitos da melhor maneira, a escolha recaiu sobre os contratos RIDE da plataforma Waves: eles não são completos para Turing e sua complexidade máxima é artificialmente limitada.
Mas vamos considerá-los apenas do lado técnico.
Além disso, para todos os contratos, a verificação formal será especialmente solicitada: como regra, é impossível corrigir um erro de contrato após o seu lançamento.
E o preço de tais erros pode ser muito alto, pois grandes quantidades de fundos geralmente são armazenadas em contratos inteligentes.
Minha máquina virtual de caracteres é escrita em PHP e Python e usa o Z3Prover da Microsoft Research para resolver as fórmulas SMT resultantes.
Na sua essência, reside uma poderosa pesquisa multi-transacional, que
permite encontrar soluções ou vulnerabilidades, mesmo que exija muitas transações.
Até o
Mythril , uma das estruturas simbólicas mais poderosas para pesquisar vulnerabilidades do Ethereum, adicionou esse recurso há apenas alguns meses.
Mas vale a pena notar que os contratos de éter são mais complexos e têm completeza de Turing.
O PHP converte o código-fonte do contrato inteligente RIDE em um script python no qual o programa é apresentado na forma de um sistema de condições contratuais e condições para suas transições compatíveis com o Z3 SMT:
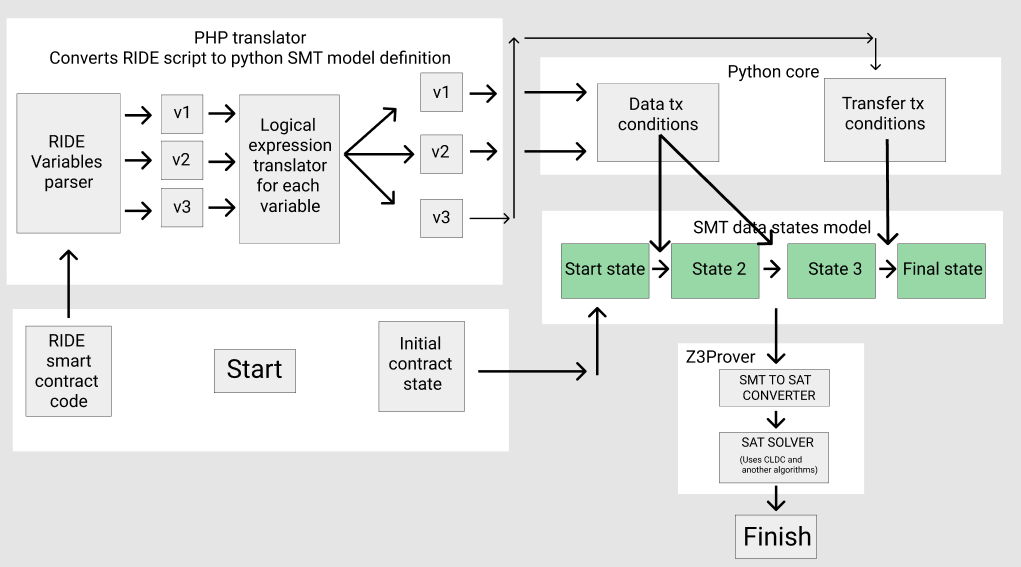
Agora vou descrever o que está acontecendo lá dentro, com mais detalhes.
Mas primeiro, algumas palavras sobre a linguagem dos contratos inteligentes RIDE.
É uma linguagem de programação funcional e baseada em expressões que é preguiçosa como pretendido.
O RIDE é realizado isoladamente na blockchain e pode extrair e gravar informações do armazenamento associado à carteira do usuário.
Você pode anexar um contrato RIDE a cada carteira e o resultado da execução será apenas VERDADEIRO ou FALSO.
VERDADEIRO significa que o contrato inteligente permite a transação e FALSO que a proíbe.
Um exemplo simples: um script pode proibir uma transferência se o saldo da carteira for menor que 100.
Como exemplo, pegarei todos os mesmos lobos, cabras e repolho, mas já apresentados na forma de um contrato inteligente.
O usuário não poderá sacar dinheiro da carteira na qual o contrato foi implantado até encaminhar todos para o outro lado.
# let contract = tx.sender let human= extract(getInteger(contract,"human")) let wolf= extract(getInteger(contract,"wolf")) let goat= extract(getInteger(contract,"goat")) let cabbage= extract(getInteger(contract,"cabbage")) # -, 4 . # . match tx { case t:DataTransaction => # let newHuman= extract(getInteger(t.data,"human")) let newWolf= extract(getInteger(t.data,"wolf")) let newGoat= extract(getInteger(t.data,"goat")) let newCabbage= extract(getInteger(t.data,"cabbage")) #0 , , 1 let humanSide= human == 0 || human == 1 let wolfSide= wolf == 0 || wolf == 1 let goatSide= goat == 0 || goat == 1 let cabbageSide= cabbage == 0 || cabbage == 1 let side= humanSide && wolfSide && goatSide && cabbageSide # , . let safeAlone= newGoat != newWolf && newGoat != newCabbage let safe= safeAlone || newGoat == newHuman let humanTravel= human != newHuman # , - . let t1= humanTravel && newWolf == wolf + 1 && newGoat == goat && newCabbage == cabbage let t2= humanTravel && newWolf == wolf && newGoat == goat + 1 && newCabbage == cabbage let t3= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage + 1 let t4= humanTravel && newWolf == wolf - 1 && newGoat == goat && newCabbage == cabbage let t5= humanTravel && newWolf == wolf && newGoat == goat - 1 && newCabbage == cabbage let t6= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage - 1 let t7= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage let objectTravel = t1 || t2 || t3 || t4 || t5 || t6 || t7 # . # 1 0, # , # - side && safe && humanTravel && objectTravel case s:TransferTransaction => # human == 1 && wolf == 1 && goat == 1 && cabbage == 1 # case _ => false }
Antes de tudo, o PHP extrai do contrato inteligente todas as variáveis na forma de suas chaves e a variável correspondente da expressão lógica.
cabbage: extract ( getInteger ( contract , "cabbage" ) ) goat: extract ( getInteger ( contract , "goat" ) ) human: extract ( getInteger ( contract , "human" ) ) wolf: extract ( getInteger ( contract , "wolf" ) ) fState: human== 1 && wolf== 1 && goat== 1 && cabbage== 1 fState: wolf: goat: cabbage: cabbageSide: cabbage== 0 || cabbage== 1 human: extract ( getInteger ( contract , "human" ) ) newGoat: extract ( getInteger ( t.data , "goat" ) ) newHuman: extract ( getInteger ( t.data , "human" ) ) goatSide: goat== 0 || goat== 1 humanSide: human== 0 || human== 1 t7: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage t3: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage + 1 t6: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage - 1 t2: humanTravel && newWolf== wolf && newGoat== goat + 1 && newCabbage== cabbage t5: humanTravel && newWolf== wolf && newGoat== goat - 1 && newCabbage== cabbage t1: humanTravel && newWolf== wolf + 1 && newGoat== goat && newCabbage== cabbage t4: humanTravel && newWolf== wolf - 1 && newGoat== goat && newCabbage== cabbage safeAlone: newGoat != newWolf && newGoat != newCabbage wolfSide: wolf== 0 || wolf== 1 humanTravel: human != newHuman side: humanSide && wolfSide && goatSide && cabbageSide safe: safeAlone || newGoat== newHuman objectTravel: t1 || t2 || t3 || t4 || t5 || t6 || t7
O PHP os converte em uma descrição do sistema Python compatível para o Z3Prover SMT.
Os dados são agrupados em um ciclo em que as variáveis de armazenamento obtêm o índice i, o índice de variáveis de transação i + 1 e variáveis com expressões definem as regras para a transição do estado anterior para o próximo.
Esse é o coração da nossa máquina virtual, que fornece um mecanismo de pesquisa multi-transacional.
fState: And( And( And( human[Steps] == 1 , wolf[Steps] == 1 ) , goat[Steps] == 1 ) , cabbage[Steps] == 1 ) final: fState[Steps] fState: wolf: goat: cabbage: cabbageSide: Or( cabbage[i] == 0 , cabbage[i] == 1 ) goatSide: Or( goat[i] == 0 , goat[i] == 1 ) humanSide: Or( human[i] == 0 , human[i] == 1 ) t7: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) t3: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] + 1 ) t6: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] - 1 ) t2: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] + 1 ) , cabbage == cabbage[i] ) t5: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] - 1 ) , cabbage == cabbage[i] ) t1: And( And( And( humanTravel[i] , wolf == wolf[i] + 1 ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) t4: And( And( And( humanTravel[i] , wolf == wolf[i] - 1 ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) safeAlone: And( goat[i+1] != wolf , goat[i+1] != cabbage ) wolfSide: Or( wolf[i] == 0 , wolf[i] == 1 ) humanTravel: human[i] != human[i+1] side: And( And( And( humanSide[i] , wolfSide[i] ) , goatSide[i] ) , cabbageSide[i] ) safe: Or( safeAlone[i] , goat[i+1] == human[i+1] ) objectTravel: Or( Or( Or( Or( Or( Or( t1[i] , t2[i] ) , t3[i] ) , t4[i] ) , t5[i] ) , t6[i] ) , t7[i] ) data: And( And( And( side[i] , safe[i] ) , humanTravel[i] ) , objectTravel[i] )
As condições são classificadas e inseridas em um modelo de script projetado para descrever o sistema SMT em python.
Modelo em branco import json from z3 import * s = Solver() Steps=7 Num= Steps+1 $code$
Para o último estado de toda a cadeia, as regras especificadas na seção de transação de transferência se aplicam.
Portanto, o Z3Prover procurará exatamente esse conjunto de condições que eventualmente permitirão que você retire fundos do contrato.
Como resultado, obtemos automaticamente um modelo SMT totalmente funcional de nosso contrato.
Você pode ver que é muito semelhante ao modelo do meu artigo anterior, que escrevi manualmente.
Modelo concluído import json from z3 import * s = Solver() Steps=7 Num= Steps+1 human = [ Int('human_%i' % (i + 1)) for i in range(Num) ] wolf = [ Int('wolf_%i' % (i + 1)) for i in range(Num) ] goat = [ Int('goat_%i' % (i + 1)) for i in range(Num) ] cabbage = [ Int('cabbage_%i' % (i + 1)) for i in range(Num) ] nothing= [ And( human[i] == human[i+1], wolf[i] == wolf[i+1], goat[i] == goat[i+1], cabbage[i] == cabbage[i+1] ) for i in range(Num-1) ] start= [ human[0] == 1, wolf[0] == 0, goat[0] == 1, cabbage[0] == 0 ] safeAlone= [ And( goat[i+1] != wolf[i+1] , goat[i+1] != cabbage[i+1] ) for i in range(Num-1) ] safe= [ Or( safeAlone[i] , goat[i+1] == human[i+1] ) for i in range(Num-1) ] humanTravel= [ human[i] != human[i+1] for i in range(Num-1) ] cabbageSide= [ Or( cabbage[i] == 0 , cabbage[i] == 1 ) for i in range(Num-1) ] goatSide= [ Or( goat[i] == 0 , goat[i] == 1 ) for i in range(Num-1) ] humanSide= [ Or( human[i] == 0 , human[i] == 1 ) for i in range(Num-1) ] t7= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t3= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] + 1 ) for i in range(Num-1) ] t6= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] - 1 ) for i in range(Num-1) ] t2= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] + 1 ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t5= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] - 1 ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t1= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] + 1 ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t4= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] - 1 ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] wolfSide= [ Or( wolf[i] == 0 , wolf[i] == 1 ) for i in range(Num-1) ] side= [ And( And( And( humanSide[i] , wolfSide[i] ) , goatSide[i] ) , cabbageSide[i] ) for i in range(Num-1) ] objectTravel= [ Or( Or( Or( Or( Or( Or( t1[i] , t2[i] ) , t3[i] ) , t4[i] ) , t5[i] ) , t6[i] ) , t7[i] ) for i in range(Num-1) ] data= [ Or( And( And( And( side[i] , safe[i] ) , humanTravel[i] ) , objectTravel[i] ) , nothing[i]) for i in range(Num-1) ] fState= And( And( And( human[Steps] == 1 , wolf[Steps] == 1 ) , goat[Steps] == 1 ) , cabbage[Steps] == 1 ) final= fState
Após o lançamento, o Z3Prover resolve um contrato inteligente e exibe uma cadeia de transações para nós, o que nos permitirá sacar fundos:
Winning transaction chain found: Data transaction: human= 0, wolf= 0, goat= 1, cabbage= 0 Data transaction: human= 1, wolf= 0, goat= 1, cabbage= 1 Data transaction: human= 0, wolf= 0, goat= 0, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 0, cabbage= 1 Data transaction: human= 0, wolf= 1, goat= 0, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 1, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 1, cabbage= 1 Transfer transaction
Além do contrato de encaminhamento, você pode experimentar seus próprios contratos ou tentar este exemplo simples, resolvido em duas transações.
let contract = tx.sender let a= extract(getInteger(contract,"a")) let b= extract(getInteger(contract,"b")) let c= extract(getInteger(contract,"c")) let d= extract(getInteger(contract,"d")) match tx { case t:DataTransaction => let na= extract(getInteger(t.data,"a")) let nb= extract(getInteger(t.data,"b")) let nc= extract(getInteger(t.data,"c")) let nd= extract(getInteger(t.data,"d")) nd == 0 || a == 100 - 5 case s:TransferTransaction => ( a + b - c ) * d == 12 case _ => true }
Como esta é a primeira versão, a sintaxe é muito limitada e podem ocorrer erros.
Nos artigos a seguir, planejo destacar o desenvolvimento futuro da VM e mostrar como é possível criar contratos inteligentes formalmente verificados com sua ajuda, e não apenas resolvê-los.
Uma máquina virtual simbólica está disponível em
http://2.59.42.98/hyperbox/As fontes estão disponíveis no github:
http://github.com/scp1001/hyperboxToda a lógica da VM está contida em 2 arquivos, hyperbox.php e hyperbox2.php