Uma dupla de matemática mapeou um território infinito de superfícies mínimas

Dois matemáticos baseados em uma teoria matemática pouco conhecida de 30 anos atrás demonstraram que superfícies mínimas semelhantes a um filme de sabão aparecem em grande número em uma grande variedade de figuras

No final de 2011, Brian White ocasionalmente ouviu uma batida na porta de seu escritório em Stanford. Lá fora, nesses momentos, dois jovens matemáticos esperavam por ele, Fernando Coda Marquez e Andre Nevis , que sempre tinham a mesma pergunta: White teria alguns minutos para ajudá-los a descobrir uma das partes obscuras de uma dissertação pouco conhecida por várias centenas? páginas escritas há trinta anos?

A dissertação, escrita por John Pitts , apresentou um poderoso mecanismo para a construção de superfícies mínimas - estruturas semelhantes a filmes e bolhas de sabão - dentro de uma ampla variedade de formas. Quando uma superfície mínima pode ser construída sobre uma figura, esta permite estudar a geometria do espaço ao seu redor. Tais superfícies aparecem em vários problemas científicos, desde o estudo de buracos negros até o desenvolvimento de biomoléculas.

E, no entanto, todos esses anos, a dissertação de Pitts ficou fora do alcance das atenções dos estudiosos - talvez porque fosse incrivelmente difícil de ler. Marquez e Nevis estavam convencidos de que havia um grande potencial nele. "Era óbvio para nós que essa teoria foi completamente subestimada e passou despercebida", disse Nevis, que atualmente é professor da Universidade de Chicago.

Embora White nunca tenha perguntado ao casal por que eles estavam interessados ​​no trabalho de Pitts, eles sempre declararam que seu interesse era "puramente acadêmico", disse Nevis. No entanto, eles tinham um objetivo definido - provar a hipótese de Wilmore há 50 anos, que aborda a questão de encontrar a melhor forma de rosquinha possível (detalhes mais adiante). Após três meses de luta com as idéias da dissertação de Pitts, Marquez e Nevis alcançaram seu objetivo , ganhando muitos prêmios e críticas positivas.

Mas nos últimos anos, eles foram capazes de levar as idéias de Pitts muito mais longe. Pitts, com seu curador, Frederick Almgren, encontrou uma maneira de garantir que cada figura em um pequeno número de dimensões tenha pelo menos uma superfície mínima. Agora, Marquez e Nevis, usando a coorte de jovens matemáticos reunidos em torno deles, com base nas idéias de Almgren e Pitts, mostraram que, no caso geral, essas formas devem conter muitas superfícies mínimas - infinitamente muitas superfícies se aglomerando em todos os cantos das figuras. "Esta é uma grande inovação", escreveu-nos a famosa geometria Karen Uhlenbeck, da Universidade do Texas, por e-mail.

"É preciso muito esforço para criar uma única superfície mínima", disse Richard Shoin, da Universidade da Califórnia, Irvine, que aconselhou Nevis há cerca de 15 anos. "O fato de haver tantos deles é incrível."

Esse renascimento da teoria de Almgren e Pitts levou a uma explosão de atividade nos últimos dois anos. "Os resultados são tão rápidos e em números tão grandes que é difícil acompanhá-los", disse White. "Parece muito interessante e maravilhoso para mim."

Marcando a cordilheira

Mergulhe o fio curvo em uma solução de sabão ou sopre uma bolha de sabão, e o líquido formará rapidamente a superfície da menor área possível. A geometria dessas superfícies mínimas ocupa matemáticos há centenas de anos. Eles aparecem em vários campos, da arquitetura, onde a superfície mínima inspira o design de telhados e outras estruturas, até a criação de micropartículas para a entrega de medicamentos. Cinco anos atrás, quando uma equipe de cientistas criou moléculas porosas capazes de transportar drogas ou hormônios dentro de si, eles descobriram que algumas das moléculas assumiam a forma de uma tireóide , uma superfície de repetição infinita, cujas partes se assemelham a um filme de sabão.

Tecnicamente, os matemáticos consideram apenas filmes de sabão em um fio como superfícies com uma superfície mínima, mas não bolhas de sabão, porque em um espaço abstrato onde não há moléculas de ar, a bolha se esvazia a um certo ponto. No entanto, o filme no fio não satisfaz totalmente os matemáticos. Sua parte interna é uma superfície lisa, mas seu fio se quebra bruscamente. É lógico pensar se é possível estender essa superfície além dos limites dos limites dos fios, para que continue parecendo uma película de sabão em cada área individual. Às vezes isso é possível, e a superfície se estende até o infinito. Às vezes, a superfície volta e cruza-se desajeitadamente consigo mesma, ou encontra outras dificuldades.


Giroide - um tipo de superfície mínima que ocorreu durante o projeto de micropartículas para administração de medicamentos

No espaço comum, isso esgota todas as possibilidades. Porém, matemáticos e outros cientistas costumam considerar outros mundos diferentes do espaço tridimensional infinito ao qual estamos acostumados - curvos ou finitos, como analogias tridimensionais de uma esfera ou superfície de um toro. Essas figuras têm novas possibilidades interessantes: superfícies mínimas que se dobram e se prendem a uma figura final fechada que não requer suporte de arame.

Na teoria da relatividade, essas superfícies mínimas finitas desempenham o papel do horizonte de eventos dos buracos negros. E se eles podem ser encontrados em qualquer figura, isso ajuda os matemáticos a considerar sua geometria de lados diferentes: eles fornecem um modelo para cortar a figura (ou coletor ) em peças potencialmente mais simples, indicam áreas de curvatura positiva dentro do coletor - em seções, curvando-se para dentro, como uma esfera ou um buraco negro, em vez de curvar-se para fora.

"Sabemos pouco sobre variedades com curvatura positiva", disse Shoin.

No entanto, muitas vezes é difícil provar a existência de uma superfície mínima dentro de uma figura. Para entender por que, considere uma versão bidimensional desse problema. A questão de encontrar a superfície mínima faz sentido em qualquer dimensão: os matemáticos simplesmente consideram a superfície uma forma cuja dimensão é um menor que o espaço em que vive. Portanto, em um mundo bidimensional, as curvas "geodésicas" compostas pelos caminhos mais curtos que conectam pontos próximos serão a superfície mínima.

Para algumas figuras bidimensionais, encontre facilmente curvas geodésicas fechadas em um loop finito. Pegue a superfície de um toro - nem mesmo necessariamente uniforme e simétrico; deixe-o apresentar irregularidades e protuberâncias. Se envolvermos uma rosquinha com um elástico passando pelo centro, podemos imaginar como a apertamos e a deslocamos para várias posições possíveis. Um deles será o mais curto - será uma curva geodésica por definição.



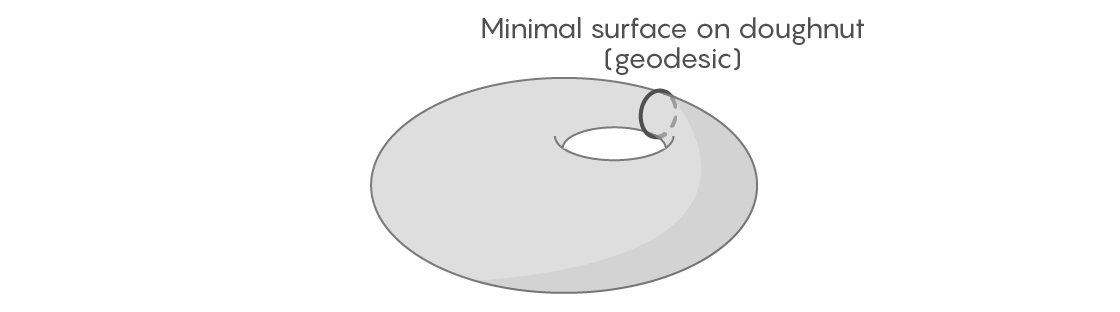
Mas se a esfera é a nossa figura, essa abordagem não funcionará mais. Em uma esfera perfeitamente plana, é fácil encontrar uma curva geodésica - será o equador e outros círculos completos. Mas em uma esfera irregular, por exemplo, na superfície da Terra, não está claro para onde vão as curvas geodésicas e se alguma delas está fechada em um loop. Você pode imaginar como envolvemos a terra com um elástico, como no caso de um donut. Mas se você começar a movê-lo, tentando encurtá-lo, ele encolherá a um ponto, porque, diferentemente de uma rosquinha, a esfera não possui um orifício para o elástico se agarrar.

No entanto, esse fiasco com um elástico é repleto de germes de sucesso. Se o equador de uma esfera redonda for interceptado por um elástico, a única maneira de alterá-lo - para adicionar ondas a ele - o tornará mais longo. Se você o mover de maneira diferente, para cima ou para baixo, para uma nova latitude, ela ficará mais curta. Portanto, o equador será a curva mais curta de um ponto de vista e a mais longa do outro.

Isso torna o equador relacionado à sela da passagem da montanha, o ponto mais alto de um lado (do caminho pelas montanhas) e o mais baixo do outro (do caminho para os picos próximos). E isso não é apenas uma analogia fraca: como regra, superfícies mínimas acabam sendo tais selas, mas suas cadeias de montanhas vivem em um mundo que é muito mais difícil de visualizar.



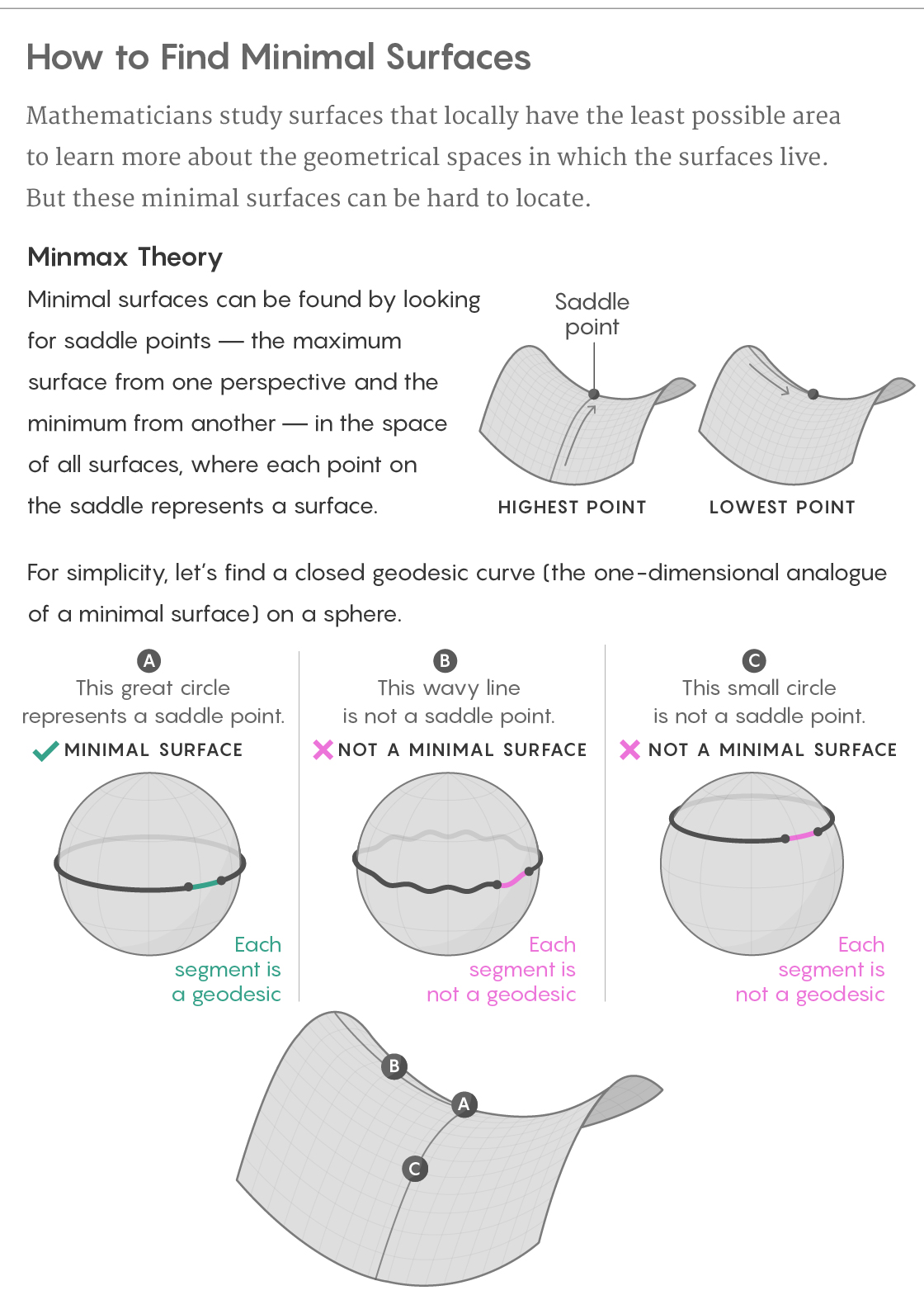
Ao determinar a superfície mínima de uma figura, podemos considerar um novo mundo que consiste em todas as superfícies finitas possíveis existentes nessa figura - a chamaremos de "superfície das superfícies". Cada ponto do espaço da superfície corresponde à superfície inteira inteiramente na figura original. Então, podemos considerar a área de cada superfície como a altura do ponto correspondente no espaço das superfícies, como resultado do qual nosso mundo terá uma topografia natural. A busca de superfícies mínimas na figura original torna-se a busca de selas no espaço da superfície.

Em 1917, George David Birkhoff usou essa abordagem para mostrar que qualquer esfera, acidentada ou lisa, deve ter uma curva geodésica fechada. Cerca de seis décadas depois, Almgren e Pitts expandiram magistralmente as idéias de Birkhoff, marcando a topografia da superfície de todas as figuras finitas em dimensões de três a sete e depois usaram essa topografia para provar que essas figuras sempre têm pelo menos uma superfície mínima fechada. A dissertação de Pitts, de 1981, sobre essa teoria da Minmax - assim chamada porque a sela é mínima e máxima - foi "absolutamente incrível", disse Nevis.

No entanto, era extremamente complexo. Poucas pessoas entenderam as nuances da teoria e alguns matemáticos que a estudaram alegaram que ela não estava totalmente confirmada, disse Shoin. "Acho que não havia dúvida de que era extremamente interessante e importante", disse ele. "Mas não estava claro o quão cheio estava."

O trabalho sobre a teoria Minmax gradualmente não deu em nada. "O trabalho de Pitts foi esquecido pela comunidade matemática por cerca de 30 anos", disse Nevis. Ela não ressuscitou até Nevis e Marquez se conhecerem em 2006 no elevador do edifício matemático da Universidade de Princeton.

Sobre a passagem da montanha

Nesse momento, Marquez chegou a Princeton para dar uma palestra; Nevis conseguiu um emprego lá logo após defender um doutorado. Ambos tinham o português como língua nativa (Marquez era do Brasil e Nevis era de Portugal), e facilmente encontraram um idioma comum. "Então eu conversei com ele pela primeira vez, mas ele conversou comigo como se fôssemos amigos por 10 anos", lembra Marquez, agora professor em Princeton.

Então eles descobriram que discutir idéias matemáticas era tão natural para eles. Eles têm estilos diferentes: Marquez é mais calmo e Nevis é mais intenso. Mas isso serviu como uma vantagem para eles. "É muito raro encontrar alguém que o complemente tão bem", disse Marquez.

Ambos estavam ansiosos para encontrar algum problema matemático complexo que pudesse ser imerso. Por vários anos, o casal lançou idéias sempre que seus caminhos se cruzavam para "ver o que estava atrasado", disse Nevis. "Tínhamos um milhão de idéias e, como resultado, uma delas foi filtrada e transformada em algo formado".

O problema filtrado acabou sendo o famoso problema da "hipótese de Wilmore". Ela sugere encontrar uma forma de toro que minimize a magnitude conhecida como energia de Willmore, que, grosso modo, mede a diferença entre uma determinada forma e uma esfera circular. Em 1965, Wilmore sugeriu que seria a rosca mais redonda de uma forma particularmente simétrica, conhecida como toro de Clifford , no entanto, apesar de muitas tentativas, a hipótese não pôde ser provada por ninguém.


Marquez (esquerda) e Nevis

Marquez e Nevis desenvolveram uma abordagem promissora, mas para funcionar, precisavam do último ingrediente: teoria do minimax. Eles pensaram que dominar essa teoria e escrever o trabalho final levaria de duas a três semanas - até que eles abrissem o livro de Pitts. “Ficamos chocados - do que se trata? - disse Nevis. "O livro estava incrivelmente seco."

Teoremas separados cresceram em muitas páginas - e isso era apenas uma descrição dos teoremas, não sua prova. O teorema principal era simplesmente difícil de encontrar. “Lembro como o Fernando veio ao meu escritório e disse: Encontrei a afirmação do teorema!” - disse Nevis.


Thor Clifford

Quando ficaram presos, jogam pôquer e pedem ajuda a White, uma das poucas pessoas que entenderam a maior parte do trabalho de Pitts (embora o próprio White tenha descrito essas conversas como "cegas, liderando cegas"; o próprio Pitts, professor da Universidade A&M do Texas, se formou escrever obras sobre a teoria do minmax algumas décadas atrás). "Estávamos incrivelmente motivados e, por isso, conseguimos avançar", lembra Nevis. "Mas isso não foi tarefa para os fracos de coração."

Quando Marquez e Nevis terminaram sua prova da hipótese de Wilmore, eles entenderam a teoria Minmax melhor do que qualquer outro matemático. Eles estavam convencidos de que seu potencial se estende muito além da própria afirmação da hipótese. "Sabíamos que tínhamos uma teoria muito poderosa", disse Nevis. - Sempre que usar o método para provar um determinado resultado que permaneceu aberto por um longo tempo, você entende que há algo nele. Isso sugere que vale a pena continuar cavando mais. "

O diagrama minmax de Almgren e Pitts produz não apenas uma sela, mas um número infinito delas. Em teoria, isso deve corresponder a um número infinito de superfícies mínimas da forma original. Almgren e Pitts não conseguiram mostrar que as superfícies mínimas obtidas dessa maneira eram diferentes. Portanto, a única coisa que definitivamente poderia ser dita era que cada figura tinha pelo menos uma superfície mínima.

Depois disso, "o desenvolvimento do tópico praticamente parou", disse Nevis. "Foi o melhor resultado por um período de mais de 30 anos."

Um novo ingrediente era necessário, e Marquez e Nevis o encontraram. A lista interminável de superfícies minmax, como mostraram em 2016, se comporta da mesma forma que as frequências do tambor.

O matemático alemão Weil, em 1911, mostrou que as frequências fundamentais do tambor têm uma propriedade inesperada: grosso modo, as altas frequências dependem apenas do volume do tambor e não de sua forma. Marquez e Nevis, juntamente com Eugene Lekumovich, do Instituto de Tecnologia de Massachusetts, mostraram que as superfícies Minmax cumprem uma lei matemática semelhante à lei das frequências de bateria. Em particular, as áreas de superfície são determinadas aproximadamente pela quantidade de espaço em que vivem, e não por sua forma.

Esse resultado, que pôs fim à hipótese apresentada várias décadas atrás, permitiu que Marquez e Nevis aparecessem em 2017 - desta vez com a ajuda de Kay Air da Universidade de Tóquio - que para a maioria das figuras a lista de minmax contém um número infinito de diferentes superfícies mínimas. Além disso, eles mostraram que essas superfícies são “densas”: elas aparecem ao lado de cada ponto no espaço circundante. A intuição que sustenta essa conclusão é que, para que o volume de espaço determine as áreas da localização de superfícies mínimas, o último deve, de alguma forma, "ver" o volume inteiro. E isso "diz que esses caras estão em toda a sua diversidade", disse Marquez.

Alguns meses depois, esse casal, junto com a estudante de graduação de Marquez, Antoine Sun , mostrou que, se você examinar a lista de superfícies minmax, verá que elas ocupam o espaço de maneira uniforme - o que os matemáticos chamam de "equidistribuição" aparece.

"Quando soube que eles eram igualmente distribuídos, fiquei surpreso", disse White. "Parecia que as pessoas não deveriam ter sido capazes de provar esse resultado durante a minha vida."

Nos últimos dois anos, vários outros matemáticos se juntaram à questão. Por exemplo, em janeiro, Xin Zhou, da Universidade da Califórnia em Santa Bárbara, com base em trabalhos anteriores de Marquez e Nevis, provou que para a maioria das figuras todas as superfícies mínimas na lista de Almgren e Pitts são diferentes umas das outras, o que coloca um ponto interessante sobre esse assunto. "Isso realmente fecha bem esse tópico, aberto desde os dias de Almgren e Pitts nos anos 80", disse White.

Essa família de resultados leva em consideração quase todas as figuras em dimensões de três a sete - com exceção das formas mais suaves, não importa quão contra-intuitivas. Mas em junho passado, Sunn conseguiu provar que cada figura nessas dimensões, incluindo as mais arredondadas, possui infinitas superfícies mínimas fechadas, o que confirmou outra hipótese de várias décadas.

Ainda não está claro se a densidade e a equidistribuição se comportarão de maneira uniforme, assim como a teoria minmax não funciona em variedades compactas ou em oito ou mais dimensões (no entanto, o novo trabalho também obteve algum sucesso aqui). Os matemáticos prevêem que seremos capazes de responder muitas perguntas mais cedo do que parecia.

"Tudo está se desenvolvendo extremamente rápido", disse Nevis. “Toda semana eu olho para o site com pré-impressões do arxiv e vejo como alguém decidiu outra coisa.”

De um ponto de vista, essas obras marcam o fim - ou o fim - de uma história que está em seu estado inacabado por quase quatro décadas. Mas este também é um novo começo: os matemáticos estão apenas começando a entender que essas novas idéias sobre superfícies mínimas podem nos dizer sobre os espaços em que vivem.

"Eu posso assumir que outras maneiras interessantes de aplicar esse conhecimento aparecerão em breve, mas o que exatamente, eu definitivamente não posso dizer", disse Shoin. "Tenho certeza de que essa será uma das principais direções da geometria".