Projeto: “Taxa de câmbio absoluta”
1. Introdução
Sobre o projeto
O projeto “ Taxa de câmbio absoluta ” está envolvido na análise de taxas de câmbio emparelhadas, na alocação de taxas de câmbio absolutas a partir delas e em suas análises.
No âmbito do projeto, foi obtida uma metodologia para a conversão de taxas de pares em taxas de câmbio absolutas. Para isso, a moeda absoluta ABS é definida. Todas as moedas disponíveis são expressas em termos de ABS.
O projeto explora as propriedades dos cursos absolutos. Várias aplicações de taxas de câmbio absolutas são investigadas.
Por que isso é ...?
Até o momento, vários artigos já foram publicados sobre a aplicação do método da taxa de câmbio absoluta. Eu trago os dois últimos.
O artigo “ Um estudo da conexão das moedas mundiais através da correlação de taxas absolutas ” descreve uma das aplicações da tecnologia das taxas de câmbio absolutas. É fornecido um método formal para calcular o relacionamento entre diferentes moedas.
O artigo " O método do portfólio de Markowitz, aplicado ao mercado de câmbio ", descreve a tecnologia anteriormente inacessível para otimizar o portfólio de moedas estrangeiras.
A pesquisa não para nessas duas aplicações. Outras aplicações de tecnologia estão sendo testadas. Se os leitores tiverem suas próprias visões de outros usos possíveis, eles poderão ser escritos na discussão do artigo. Links para sites de discussão são fornecidos.
Metodologia para obtenção de cursos absolutos
Uma descrição detalhada da tecnologia é fornecida no artigo " De pares de moedas a taxas de câmbio absolutas ".
O método baseia-se na análise da apresentação de cursos emparelhados. Uma taxa de câmbio de pares é a razão entre o valor de uma moeda e o valor de outra. E se você introduzir algum ABS universal de moeda absoluta, ocorrerá a seguinte transformação.
Uma taxa de câmbio de pares é a razão de duas taxas absolutas.
Para obter cursos absolutos, você deve primeiro fazer o prólogo da equação.
Dessa forma, pode-se observar que os logaritmos das taxas de pares estão linearmente relacionados aos logaritmos das taxas de câmbio absolutas. E isso significa que você pode procurar uma transformação linear simples entre eles. Os logaritmos dos cursos absolutos podem ser multiplicados pela matriz de conversão direta e obter os logaritmos dos cursos emparelhados.
E devemos esperar que haja uma transformação linear inversa para a transição de cursos em pares para cursos absolutos.
Por conseguinte, toda a metodologia para a obtenção de cursos absolutos é escrita da seguinte maneira.
Você só precisa registrar os cursos emparelhados, multiplicá-los pela matriz inversa e aplicar o expoente.
Sobre o problema
Foi descrito acima como obter cursos absolutos de duplas. Isso é feito usando uma transformação linear das taxas de pares logarítmicos e retorno através do expoente.
A conversão linear direta de taxas absolutas para taxas emparelhadas é feita usando uma matriz direta. Obtê-lo é muito simples. Consiste em zeros, uns e menos (o "0" significa que não há relação par / moeda, "+1" significa a moeda no numerador do par, "-1" significa a moeda no denominador do par). Abaixo você pode vê-lo.
O maior problema é obter a matriz inversa (mais precisamente, você precisa usar a transformação pseudo-inversa ). Com sua ajuda, você pode ir de cursos em pares para cursos absolutos. Mas a obtenção dessa matriz não é trivial devido à degeneração da matriz de transformação direta.
No artigo anterior, é apresentada uma descrição de um método para obter essa matriz. No artigo “ Detalhes da transição das taxas de câmbio do par (relativo) para o absoluto. Work on bugs ”revela um método para obter cursos absolutos. No experimento, usamos a técnica de transição para componentes linearmente independentes. Assim, foi possível livrar-se da degeneração na transformação pseudo-inversa.
Método do presente experimento
Neste artigo, outro método para evitar a degenerescência na matriz de transformação direta é proposto. Atualmente, os cursos emparelhados são fornecidos pela RBC . Existem 88 pares de moedas para exportação. Para eles, a seguinte matriz de transformação direta existe.
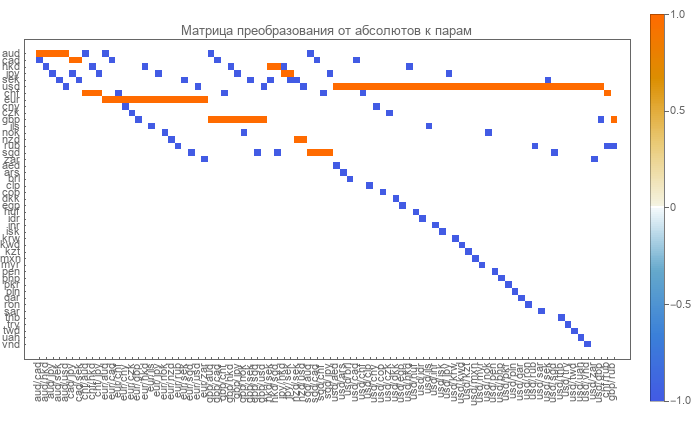
Zeros brancos, azul -1 e vermelho são unidades. Mas é degenerado. I.e. não produzirá uma matriz inversa.
Durante o experimento anterior, foi possível notar que uma matriz diagonalmente semelhante tem uma transformação inversa. Consequentemente, foi proposta uma mudança para taxas cruzadas e uma matriz de transformação não degenerada .
Todo o cálculo foi realizado no sistema Wolfram Mathematica . O sistema permite que você receba cursos cruzados diretamente dentro do sistema .
Detalhes do experimento (pequeno exemplo)
Há um total de 45 moedas. Para maior clareza, primeiro consideramos o caso com um pequeno número de moedas e pares de moedas. O cálculo está disponível no link na Nuvem Wolfram .
Lista de moedas e pares de moedas
As 10 moedas a seguir foram selecionadas: AUD, CAD, HKD, JPY, SEK, USD, CHF, EUR, CNY, CZK. Desses, 9 pares de moedas foram determinados: AUD / CAD, CAD / HKD, HKD / JPY, JPY / SEK, SEK / USD, USD / CHF, CHF / EUR, EUR / CNY, CNY / CZK.
Matriz de conversão direta
A matriz de transformação direta tem o seguinte formato.

A versão colorida fica assim.

O tamanho da matriz é 10x9. A classificação da matriz é 9. A matriz não é degenerada. Você pode procurar livremente o oposto a ele.
Matriz de transformação inversa de emparelhado para absoluto
Como resultado da aplicação do método de transformação pseudo-inversa, obtemos a matriz inversa.

De forma colorida assim.

O tamanho da matriz inversa é 9x10.
Verificação de matriz inversa
Antes de prosseguir, verifique a matriz resultante. Para fazer isso, multiplicamos a matriz inversa pela linha reta. O resultado é o seguinte.

E na forma colorida.
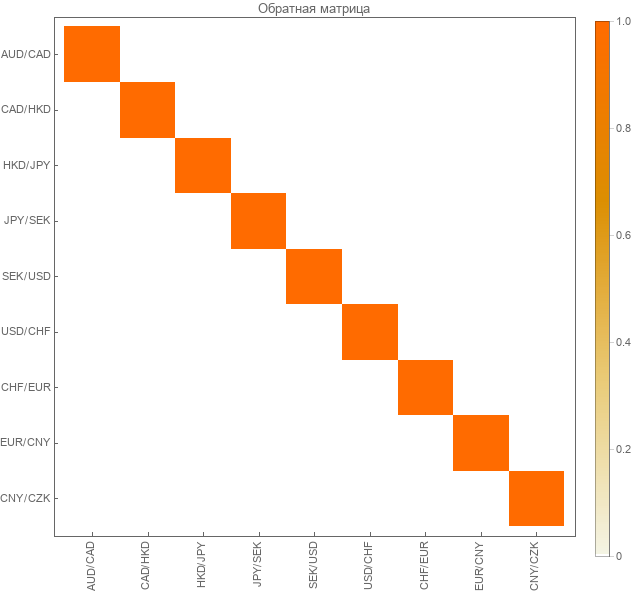
Realmente tenho a matriz diagonal da unidade . Então o inverso é verdadeiro.
Em um experimento anterior , testamos o método para obter taxas absolutas. Para isso, a partir dos cursos absolutos obtidos, os cursos em pares foram restaurados através da matriz de conversão direta. Em seguida, comparamos os cursos emparelhados restaurados com os originais e analisamos o erro. No nosso caso, o erro nessa verificação estará dentro dos limites de precisão da máquina.
Teste em cursos reais
Agora vamos ver os resultados em dados reais. Vamos fazer cotações reais de taxas cruzadas de moedas em pares e calcular as taxas absolutas para elas.
Fizemos cursos diários diários por 30 dias, de 28/03/2019 a 27/04/2019.
Taxas de par de moedas
Aqui está uma matriz de taxas de câmbio emparelhadas. Estas são as colunas do par de moedas para os seguintes pares AUD / CAD, CAD / HKD, HKD / JPY, JPY / SEK, SEK / USD, USD / CHF, CHF / EUR, EUR / CNY, CNY / CZK.

Aqui está o gráfico para um dos pares de moedas.

Os valores médios para cursos em pares foram os seguintes.
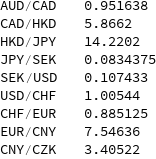
Agora vamos tentar avaliar a variabilidade dos dados. Para fazer isso, use o desvio padrão . Mas, para padronização, dividimos pelo valor médio. Exibimos os resultados no gráfico.
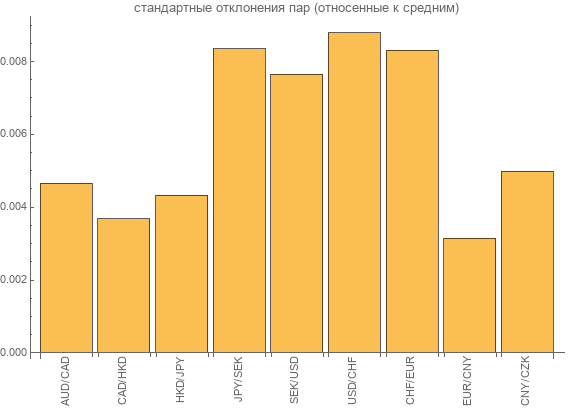
Como você pode ver, os desvios padrão para cada par de moedas estão no intervalo de 0, 2% a 0, 9% dos valores médios das taxas de pares.
Cursos Absolutos
Agora calculamos cursos absolutos para emparelhados (a metodologia é descrita na seção Metodologia para obtenção de cursos absolutos). Após os cálculos, obtemos a seguinte série de dados.
Estas são colunas de câmbio absolutas para as seguintes moedas: AUD, CAD, HKD, JPY, SEK, USD, CHF, EUR, CNY, CZK.

Aqui está um gráfico da taxa absoluta de uma das moedas.
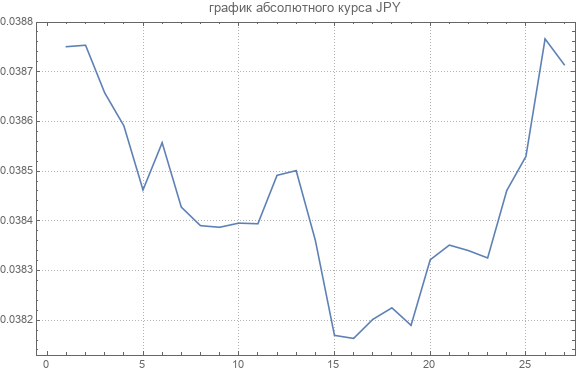
Os valores médios para cursos absolutos são os seguintes.

Estimamos a variabilidade das taxas de câmbio absolutas.

Os desvios padrão para as taxas absolutas de cada moeda estão na faixa de 0, 2% a 0, 7% dos valores médios das taxas absolutas. E isso é consistente com os dados para pares de moedas.
Resultados em todas as moedas
Agora considere os resultados em todas as moedas disponíveis. A fonte de cálculo está disponível aqui .
Lista de moedas e pares de moedas
A lista completa contém as seguintes 45 moedas: AUD, CAD, HKD, JPY, SEK, USD, CHF, EUR, CNY, CZK, GBP, ILS, NOK, NZD, RUB, SGD, ZAR, AED, ARS, BRL, CLP, COP , DKK, EGP, HUF, IDR, INR, ISK, KRW, KWD, KZT, MXN, MYR, PEN, PHP, PKR, PLN, QAR, RON, SAR, THB, TENTE, TWD, UAH, VND. Os 44 pares de moedas a seguir foram selecionados para eles: AUD / CAD, CAD / HKD, HKD / JPY, JPY / SEK, SEK / USD, USD / CHF, CHF / EUR, EUR / CNY, CNY / CZK, CZK / GBP, GBP / ILS, ILS / NOK, NOK / NZD, NZD / RUB, RUB / SGD, SGD / ZAR, ZAR / AED, AED / ARS, ARS / BRL, BRL / CLP, CLP / COP, COP / DKK, DKK / EGP, EGP / HUF, HUF / IDR, IDR / INR, INR / ISK, ISK / KRW, KRW / KWD, KWD / KZT, KZT / MXN, MXN / MYR, MYR / PEN, PEN / PHP, PHP / PKR, PKR / PLN, PLN / QAR, QAR / RON, RON / SAR, SAR / THB, THB / TRY, TRY / TWD, TWD / UAH, UAH / VND.
Matriz de conversão direta
Temos uma matriz de transformação direta do tamanho 45 por 44. Sua classificação é 44.
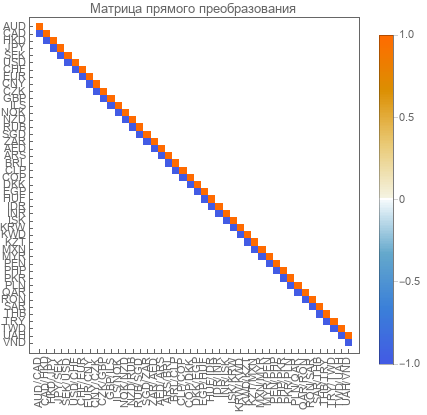
Matriz de transformação inversa
A matriz inversa é o resultado da aplicação de pseudo-transformação inversa. O tamanho da matriz é 44 por 45.
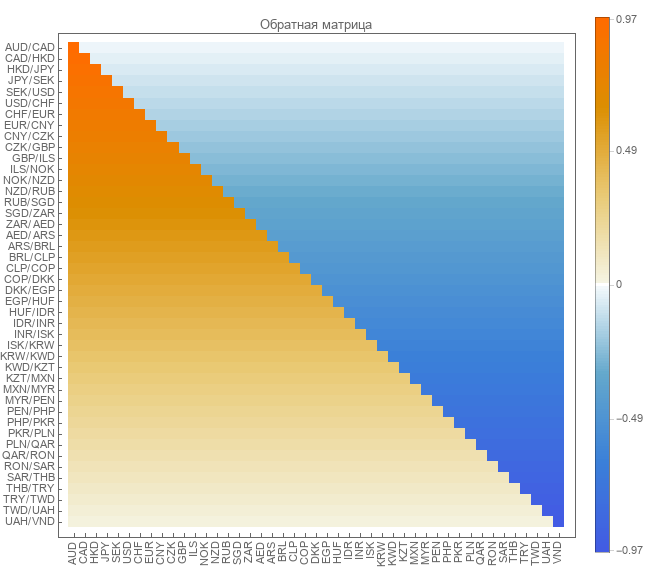
Verificação de matriz inversa
Após multiplicar a matriz inversa pela reta, obtivemos a matriz de identidade.
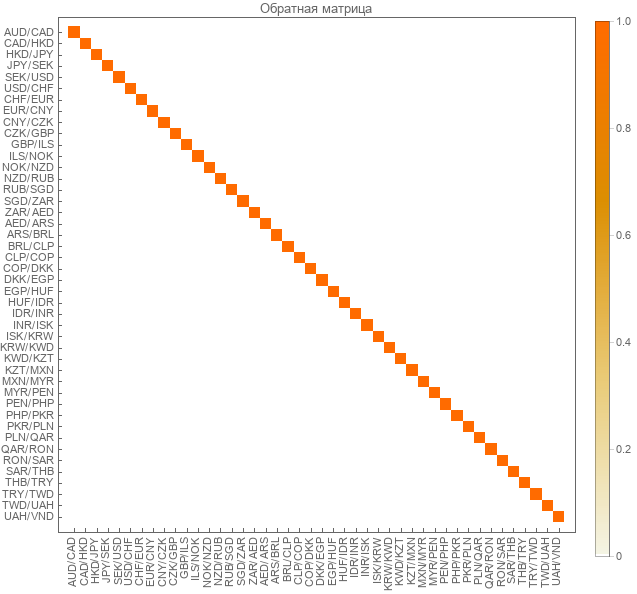
Teste em cursos reais
Carregou 44 taxas de câmbio entre moedas. Um exemplo de um é dado no gráfico a seguir.
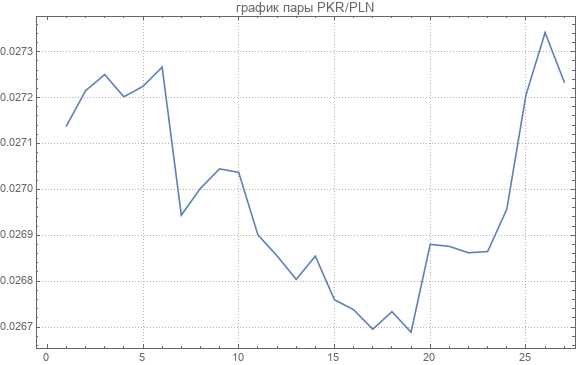
Aqui estão as taxas de câmbio médias para cada par de moedas.
AUD / CAD 0,951638
CAD / HKD 5.8662
HKD / JPY 14.2202
JPY / SEK 0,0834375
SEK / USD 0,107433
USD / CHF 1,00544
CHF / EUR 0,885125
EUR / CNY 7,54636
CNY / CZK 3.40522
CZK / GBP 0,0335481
GBP / ILS 4.69022
ILS / NOK 2.38106
NOK / NZD 0,173451
NZD / RUB 43.5338
RUB / SGD 0,0209621
SGD / ZAR 10.4641
ZAR / AED 0,259015
AED / ARS 11.7136
ARS / BRL 0,0907021
BRL / CLP 171,256
CLP / COP 4.72058
COP / DKK 0,00210715
DKK / EGP 2.60095
EGP / HUF 16.5291
HUF / IDR 49.5307
IDR / INR 0,00490364
INR / ISK 1.73912
ISK / KRW 9.44975
KRW / KWD 0.000266945
KWD / KZT 1248.05
KZT / MXN 0.050062
MXN / MYR 0,216251
MYR / PEN 0.803967
PEN / PHP 15.7631
PHP / PKR 2.71475
PKR / PLN 0,0269842
PLN / QAR 0,954411
QAR / RON 1.16298
RON / SAR 0,885697
SAR / THB 8.48908
THB / TRY 0.179564
TRY / TWD 5.39876
TWD / UAH 0,871089
UAH / VND 863.675
Para cada par de moedas, analisamos a variabilidade como na experiência acima.

O desvio padrão para todos os pares de moedas varia de 0,2% a 2,5% da média.
Após a recontagem, obtemos taxas absolutas. Aqui está um gráfico da taxa absoluta de uma das moedas.
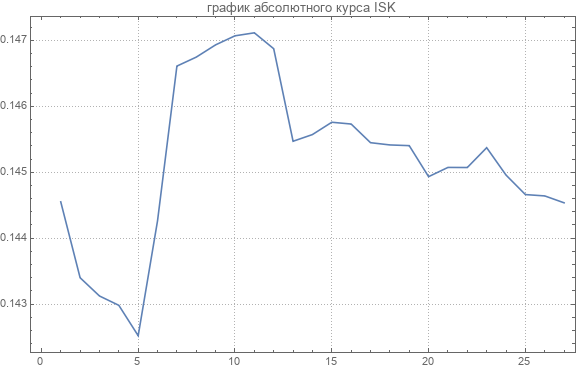
Os valores médios das taxas absolutas foram os seguintes.
AUD 12.4626
CAD 13.096
HKD 2.23247
JPY 0.156996
SEK 1.88165
USD 17.5149
CHF 17.4213
19,6824 EUR
CNY 2.60821
CZK 0.765955
GBP 22.832
ILS 4.86814
NOK 2.04455
NZD 11.7884
RUB 0.270822
SGD 12.9197
ZAR 1.23485
AED 4.76765
ARS 0.407218
BRL 4,49018
CLP 0.0262207
COP 0.0055548
DKK 2.63619
EGP 1.01359
HUF 0.0613224
IDR 0,00123809
INR 0,25249
ISK 0.145194
KRW 0.0153652
KWD 57.5605
KZT 0.0461203
MXN 0,921362
MYR 4.26106
PEN 5.30007
PHP 0,336241
PKR 0.123862
PLN 4.59025
QAR 4.8096
RON 4.1356
SAR 4.66938
THB 0.550046
TRY 3.06473
TWD 0.567676
UAH 0.651731
VND 0.000754602
A variabilidade das taxas absolutas pode ser estimada pelo diagrama.

O desvio padrão de todas as taxas absolutas varia de 0,2% a 2,5% da média. O que é consistente com os dados dos pares de moedas.
Conclusões
O experimento com a obtenção de cursos absolutos a partir de cruzamentos pareados foi um sucesso. Um novo método para calcular taxas absolutas foi obtido. O método funciona e é facilmente aplicável. Para mais pesquisas, é fácil o suficiente para receber cursos absolutos.
A precisão do método é limitada apenas pela precisão dos cursos transversais emitidos.
Infelizmente, taxas cruzadas de código aberto não podem ser encontradas na rede. E, portanto, esse método não pode ser aplicado no site. Porém, na comparação inicial dos cursos absolutos do local e os obtidos no presente experimento, as diferenças foram reveladas apenas na quarta casa decimal. Faremos uma comparação detalhada nos seguintes trabalhos.
A versão mais recente deste artigo em formato PDF pode ser baixada aqui .
Enin A.V.
Orenburg
02/02/2019