Os anos oitenta chegaram ao mundo. A IBM conquistou o mercado de computadores profissionais com seu PC e PC XT, os precursores de todos os computadores desktop modernos. Jobs, um após o outro, lançou novos modelos da Apple. O Commodore 64 e o ZX Spectrum agitavam-se em todo o mundo. Enquanto isso, o Ascota 170 - computadores mecânicos do início dos anos 50 continuava sendo produzido no bloco soviético. Por alguma razão, no RuNet (e no resto da Internet também) eles falam pouco sobre essas máquinas incríveis, quase as únicas em série (mais de trezentos mil de 1955 a 1983) produzidas por computadores mecânicos completos de Turing. Eu mesmo descobri sobre eles apenas quando Ascot acidentalmente caiu em minhas mãos.
Espero que meu artigo possa mudar isso.
Meu Ascot terminou de contar a raiz quadrada de 2.Em geral, sou colecionador de máquinas de calcular mecânicas. Infelizmente, esses carros geralmente são pesados, e eu não tenho um museu de tamanho infinito, então tenho que pegar apenas o mais interessante. Então, quando Sergey Frolov perguntou se eu precisava de Ascot, pesquisei no Google por alguns minutos e descobri que o Ascot era chamado de carros muito chatos e primitivos da RDA, que não valem o lugar que ocupam. O que Sergey disse. Felizmente, Sergey respondeu que não se tratava apenas de Ascot, mas de um modelo particularmente raro 170. Voltei a pesquisar no Google e fui capturado.
Aconteceu que me ofereceram uma das máquinas mecânicas mais complicadas já produzidas, uma máquina de calcular contabilidade programada com a ajuda de "pregos" presos em uma placa especial com um martelo. Infelizmente, a comunicação com o vendedor no Avito mostrou que o Ascot estava incompleto, portanto, levá-lo foi inútil. Então outra metade da Ascot apareceu no Avito (o vendedor tentou me provar por mais de uma hora que ela estava inteira, não a metade), depois a pergunta permaneceu por um ano ... E então o primeiro vendedor me escreveu e disse que havia encontrado as peças que faltavam! Aqui o pano de fundo termina e a própria história começa.
É claro que, neste ponto, li que o Ascot-170 é como uma máquina programável. Mas "programável" é um conceito flexível e, antes de comprar, tentei aprender algo sobre suas capacidades. Felizmente, isso acabou sendo simples: o Ascot foi entregue em massa à URSS e dezenas de livros foram publicados sobre eles. Comprei um deles, um folheto fino sobre métodos de aplicação, no Avito - mas entendi, infelizmente, um pouco - basicamente, que a máquina trabalha constantemente em um ciclo e de alguma forma suporta transições. Não sei o que faria com essa informação - mas a idéia me veio à mente: na estação de metrô da Biblioteca Lenin, há a Biblioteca Lenin! Ao longo do século XX, cópias obrigatórias de livros publicados em nossa casa reuniram-se lá, e livros sobre Ascot deveriam estar lá. De fato, no catálogo eletrônico de Leninka
havia mais de trezentos livros mencionando o Ascot 170 . Além disso, constatou-se que, nas últimas décadas, o modo de operação da biblioteca diminuiu bastante e hoje qualquer pessoa pode vir e tirar fotos de livros em uma câmera não profissional.
Para comemorar, fotografei várias dezenas de livros e compreendi com eles que Ascot podia, e imediatamente comprei. E ele fez um estudo detalhado dos livros didáticos.
Oportunidades Ascot 170
Ler esses livros não foi fácil: eles não apenas descreveram a programação de uma máquina desenvolvida muito antes do advento da primeira linguagem de alto nível, Fortran. Então eles também foram escritos em termos contábeis. Em geral, imagine que você precise estudar um livro sobre
1C: Assembler , escrito em Old Slavonic, e entenderá aproximadamente a escala do problema que me confrontou. Basta dizer que eu pude estabelecer o fato da presença de um operador condicional apenas porque eu o procurei especificamente. E para entender como funciona, só foi possível depois de estudar o design dos nós correspondentes e uma série de experimentos.
Sim Ascot tem declarações condicionais! E as equipes de transição! Em geral, tudo o que você precisa para um computador de uso geral completo!
Deixe-me contar um pouco mais sobre isso. Usarei o pseudocódigo do tipo C que eu inventei - completamente diferente do usado em livros antigos, mas muito mais compreensível hoje.
Portanto, durante a operação, o transporte da máquina se move da direita para a esquerda em relação ao corpo da máquina - como em uma máquina de escrever convencional. Ao mesmo tempo, a unidade de impressão desliza ao longo do papel e a unidade de leitura do comando do programa - em relação à placa do programa com orifícios nos quais os pinos e os pés estão inseridos - é aproximadamente a mesma que no tambor da caixa de música. Em algum momento, o nó de leitura encontra paradas colunares, significando "você precisa parar aqui e fazer alguma coisa", para e faz o que o restante das colunas nesta coluna e as teclas pressionadas pelo operador exigem. E se o nó de leitura não encontrar as paradas para o final do carro, o carro se moverá automaticamente da direita para a parada e a verificação será iniciada novamente - esse é o ciclo principal em que o programa gira sem parar.
Uma coluna de paradas. Vertical acima das colunas, o restante - software.Na prática, essas paradas "precisam fazer alguma coisa", isto é, as etapas do programa, pode haver cerca de 50 em uma placa. Vários comandos podem ser executados em uma única etapa. Por exemplo, esse código leva apenas uma etapa:
if (I>0) { print(K); I+=K; II-=K; III-=K; goto program2;
Como você pode ver, a máquina acessa ativamente os registros; registradores são filas de engrenagens no corpo da máquina, de modo que a memória do programa (placa com paradas) seja separada da memória de dados (fileiras de engrenagens de registradores). No total, a máquina possui ~ 50 etapas de memória de comando (~ 0,3 kB) e 56 registros inteiros de 12 casas decimais (outras 0,3 kB).
Em uma etapa, a máquina pode ler um registro, imprimir seu conteúdo, adicionar ou subtraí-lo a vários outros registros e redefini-lo. Ao mesmo tempo, são executadas algumas opções para comparar com zero e várias opções para comandos de transição.
Infelizmente, apesar da complexidade e riqueza do código de máquina, ele tem várias limitações desagradáveis:1. A máquina não possui comandos para multiplicação e divisão.
Curiosamente, isso não é um bug, é um recurso. A maioria das máquinas contábeis mais simples tem um comando de multiplicação, mas os desenvolvedores da Ascot já no início dos anos 50 perceberam que os dias da mecânica estavam contados e, em vez de um multiplicador mecânico lento e desajeitado, eles forneceram a capacidade de conectar um módulo matemático externo. De fato, referências ao multiplicador mecânico externo para Ascot são encontradas em livros didáticos antigos, mas nenhuma de suas fotografias reais (ou, especialmente, de espécimes reais) foi preservada. Já no final da década de 1950, começaram a ser utilizados módulos de lâmpadas R12 (monstros do tamanho de um pequeno gabinete, pesando 200 kg e um consumo de um quilômetro e meio). Em 1962, foram produzidos pequenos multiplicadores de transistor (com uma pequena unidade de sistema) e, quando deixaram o transportador Na minha instância do Ascot, pequenos divisores de chips foram usados. Em geral, é bom que eu tenha uma cópia sem divisão de multiplicação: seria uma pena obter uma calculadora eletrônica banal em microcircuitos, em vez de um computador totalmente mecânico.
2. A máquina não sabe como deslocar um número por um dígito para a direita ou esquerda.
Em geral, é possível organizar programaticamente multiplicação, divisão e outras matemáticas complicadas; de fato, muitos processadores RISC modernos fazem exatamente isso. A Ascot também poderia ter feito isso - mas, infelizmente, para isso você precisa mudar o número por dígito, e esse comando não é fornecido. Na verdade, isso é muito estranho, porque o módulo multiplicador, especialmente no início, era caro e raro, e a máquina tem todo o necessário para organizar a mudança. Eu até quero adicionar um comando shift ao meu Ascot - mas mais sobre isso no final do artigo.
3. O número de marcas de salto é limitado.
Pode haver marcas para trás1, para trás2, para frente1 e para frente2 no programa, cada uma delas várias vezes, as etapas do programa podem ser marcadas como executadas de acordo com o programa 1, de acordo com o programa 2 e ambos. Parece bom, mas ao programar um algoritmo bastante complexo, isso é suficiente para diminuir.
4. Não há suporte para matrizes e endereçamento indireto.
Ascot tem muitos registros. Pense bem: há 50 etapas do programa, para cada etapa você pode ler (e imprimir) apenas um registro - e existem 56 registros! Ou seja, o endereçamento direto de todos os registros no modo automático, sem selecionar um número de registro no teclado, é impossível em princípio.
Normalmente, esse problema é resolvido usando diferentes opções de endereçamento indireto - por exemplo, você primeiro define o número do registro (ptr = & R00) e, em um loop, aumenta-o repetidamente (ptr ++). E, em princípio, o Ascot tem tudo para isso: cinquenta registros são organizados na forma de cinco rolos rotativos, dez registros cada e, para endereçamento incremental, bastava adicionar o comando para girar o tambor um passo à frente. Para contar pilhas de documentos com várias linhas, essa seria uma função muito popular. Mas eles não o fizeram, por algum motivo. A única explicação que me ocorreu foi que, no início da década de 1950, o endereçamento incremental ainda não havia sido inventado. Se alguém se lembrar de um computador alemão anterior com endereçamento incremental - diga-me, por favor.
Living Ascot!
Enquanto lidava com os recursos de programação, um computador veio de Omsk. Depois de uma briga inevitável com os carregadores, coloquei-o no meio da sala, bati na ferrugem com um martelo, derramei uma mistura de óleo e querosene no mecanismo e tentei ligá-lo.
Ascot (à direita) era muito grande
E muito sujoComo esperado, ele não funcionou. Entrei, peguei um punhado de lixo, sacudi o pino, o carro deu partida pela primeira vez, dei alguns movimentos e congestionei.
O mês seguinte estava em reparo. Eu cobri a metade da Internet com anúncios para encontrar um instalador experiente, encontrei várias pessoas que, quarenta anos atrás, tinham um pequeno negócio com a Ascot, mas, infelizmente, eu mesma tive que consertar. Imprimi uma caneta em uma impressora 3D para girar manualmente o eixo de controle, aprendi como desligar os contadores presos, peneirei mais alguns pedaços de casca de abeto especialmente maliciosa do mecanismo, encontrei e desenvolvi meia dúzia de juntas presas, consertou meia dúzia de molas com falha.
De onde é a casca ?!Eu pulei o trabalho por semanas, vasculhei de manhã à noite no manual de instalação, procurando a causa do próximo mau funcionamento, peguei spammers no patamar que, por cem rublos, me ajudaram a virar temporariamente a máquina de cabeça para baixo ... E finalmente cheguei ao ponto em que era possível iniciar o carro "Olá mundo!".
Alternamos o Ascot para o modo de máquina de escrever e digite "NELLO SHORD".Hum, não, é fácil demais. Vamos tomar coelhos imortais melhor.
Suponhamos que não tivéssemos coelhos há um mês e hoje compramos alguns coelhos no mercado.
Depois de um mês, eles crescem em um par de coelhos adultos.
Depois de mais um mês, o casal dá à luz e temos dois coelhos adultos e dois coelhos. Total de dois pares.
Um mês depois, um casal de adultos dá à luz novamente, e os coelhos do último casal crescem e se tornam adultos. Total, três casais, dois adultos e um filho.
Depois de mais um mês, dois pares de adultos dão dois pares de filhotes, e os coelhos do último mês crescem. No total, temos cinco pares, todos os coelhos que estavam conosco há um mês, adultos e todos os adultos deram um par de filhotes.
E assim por diante
Esse problema foi estudado no início do século XIII pelo matemático italiano Fibonacci, em cuja honra a série de números resultante é chamada de série Fibonacci:
0 1 1 1 + 1 = 2 1 + 2 = 3 2 + 3 = 5 3 + 5 = 8 5 + 8 = 13 8 + 13 = 21 ...
Vamos calcular no Ascot. É simples Deixando no registro I, temos um membro ímpar da série (para iniciantes, o primeiro), no registro II - par (para iniciantes, zero). Então o programa ficará assim:
1: read I; II+=; prn();
O programa deve ser montado manualmente e, em seguida, direcione as paradas nos orifícios desejados na placa do programa. O resultado é este:
1 0/0 12/4 14/3
1 12/3 14/4 17/4 33/4
Aqui, aquele no início significa o batente da coluna tipo 1, que faz a máquina parar para executar essas etapas de acordo com o programa nº 1, 0/0 (definido na linha nº 0 para o tipo 0) força a máquina a procurar por batentes de coluna a partir deste ponto. As paradas na linha 12 controlam o registro II: 12/3 faz a leitura do registro e 12/4 - adiciona o número de leitura a ele. Da mesma forma, 14/3 faz com que a leitura do registro I e 14/4 - acrescentando-lhe a leitura. A impressão do número de leitura ocorre automaticamente, a menos que uma parada especial de 5/3 seja instalada que desative a impressão. 17/4 gira o rolo do carro um passo e 33/4 inicia o retorno do carro (essa parada pode ser omitida, o carro desliza até o fim e o retorno do carro começa automaticamente).
Para o bem, você precisa adicionar outro 15 / 6R às duas linhas e, imediatamente após o final da etapa, a máquina inicia a próxima. Mas a primeira vez que não o fiz, tive que pressionar constantemente a tecla Iniciar.
Curiosamente, o programa foi iniciado pela primeira vez. Fiquei emocionado!
Mas, para executar este programa, você deve primeiro gravar os dados nos registros desejados e, em seguida, os resultados são exibidos em duas colunas imprecisas. Vamos criar um programa que solicitará os dados de origem e, em seguida, exibirá os membros da série e seus números.
Acontece assim:
1: read I; clr;
Comecei o programa e o carro atolou com segurança, porque antes eu não tinha usado o registrador K e tinha outro pedaço de casca. Nde. Ele removeu um pedaço de casca, desligou o balcão e encostou o carro. E funcionou!
Decidi que a máquina já está finalmente funcionando, você só precisa digitar um algoritmo bonito para se gabar de Habré e escrever um relatório. Por exemplo, Stanley Frenkel, de acordo com o Sr. Feynman, ensinou o tabulador a contar como tangente. Por que eu sou pior? Isso é compreensível, pior, mas de repente?
Infelizmente, não encontrei algoritmos adequados. No Stackowerflow, eles sugeriram uma opção de cálculo de logaritmo que era muito complicada para o Ascot; na Biblioteca Lenin havia
algumas brochuras com vários algoritmos interessantes - mas também eram muito difíceis para o Ascot. No final, cuspi em trigonometria e logaritmos e decidi criar a raiz quadrada banal.
Em geral, a raiz quadrada é considerada fácil. A partir da fórmula da soma dos termos da progressão aritmética, verifica-se que a soma dos primeiros n números ímpares = n ^ 2. O que segue
De onde é relativamente fácil derivar o algoritmo de raiz quadrada usado desde o início dos anos 50 pelos aritmômetros automáticos de raiz quadrada de Friden -
aqui está um pouco mais detalhadamente . É verdade que esse algoritmo também exige mudanças por descarga, mas apenas por descarga (a troca por descarga, ou seja, multiplicando por dez, pode ser organizada como uma série de adições, e a troca por descarga usando os recursos do Ascot é praticamente impossível).
A primeira versão do programa que escrevi à noite. Mas, devido ao número de operações necessárias ao subir, ele não conseguiu se ajustar em 50 etapas. Eu tive que otimizar calculando dois turnos diferentes com os mesmos comandos, corrigir os erros, depurar o programa em um pedaço de papel, corrigir os erros novamente, depurar novamente ... Em algum lugar de uma semana, chegou a montagem, preenchimento na placa do programa e teste. Não deu certo.
Verificado novamente, encontrou alguns erros menores. Corrigido. Não deu certo. Reli os livros e descobri que não entendi uma sutileza da programação. Corrigido, não funcionou. Verificado novamente, encontrou outro erro. Não deu certo. Eu verifiquei duas vezes, percebi que não havia consertado um pequeno defeito no carro. Corrigido. Não funcionou ... Em geral, por mais uma semana eu estava configurando um programa em hardware. E finalmente depurado!
Espero que, depois disso, não haja mal-entendidos graves sobre mau funcionamento da programação e da máquina, porque a calculadora da raiz quadrada parece usar todas as funções computacionais e lógicas que estão na máquina. Isso não é todos os registros, mas eu verifiquei os registros separadamente.
Qual é o resultado e o que vem a seguir?
Como resultado, em primeiro lugar, tenho um Ascot-170 funcionando.
Em segundo lugar, espero que este artigo tenha tornado mais famoso no RuNet. O Ascot foi usado conosco pelo menos até o final dos anos 80, e só posso explicar sua baixa fama pelo fato de poucas pessoas entenderem o quanto elas eram legais, e os donos dos armazéns não entenderam o quanto eles eram valiosos. Talvez o artigo corrija essa situação.
Em terceiro lugar, criei uma
seção no Ascot no meu site, na qual publiquei um guia de programação, algumas dicas sobre como configurar um mecanismo, livros, modelos para impressão 3D, códigos de programa etc. Espero que isso também sirva para popularizar o Ascot e ajude os avaliadores, que serão capazes de obtê-lo depois de mim.
Quarto, no decorrer do trabalho, tentei levar o tempo gasto no Ascot para o tablet. Então, passei menos de duzentas horas de trabalho além da procrastinação. Talvez você possa entrar no currículo, certo?
Por outro lado, alguns problemas não resolvidos permaneceram.
Primeiro, nunca criei um programa para calcular algo interessante, como funções trigonométricas, graus racionais ou logaritmos. Como eu já disse, não consegui encontrar nem encontrar um algoritmo adequado, mas se algum dos leitores do artigo me oferecer (nos comentários, em um email pessoal ou em mim [a] alple.net mail) qualquer algoritmo adequado (em pseudo-código como o
que é a raiz quadrada ), tentarei definitivamente implementá-lo em hardware e filmar sobre este vídeo.
Em segundo lugar, como eu disse, o Ascot realmente não tem uma mudança para executar o comando. Ao mesmo tempo, tenho a impressão de que eles fariam isso, mas não o fizeram - não posso explicar de outro modo a existência dos registros III / IV.
sobre registrosVariedades de Ascot foram produzidas com um conjunto diferente de registros. O maior número deles, 55 (+1 no teclado), está apenas na minha versão. Aqui está uma lista deles:
Registro do teclado no qual o número digitado no teclado é armazenado temporariamente.
Os registros I e II são universais, completamente independentes, controlados automaticamente e pelo teclado, suportando números negativos e operações lógicas.
Registre K - controle, para controlar a operação sem erros do operador e da máquina. A função é semelhante a I e II, além de ter proteção contra redefinição acidental. Não é controlado pelo teclado, mas, para um registro de controle, é uma virtude.
Os registros acumulados são os mesmos, em tambores de 10 peças. Eles não funcionam com números negativos e são menos usados em operações lógicas, possuem algumas limitações técnicas de conexão mútua, são normalmente controlados a partir do teclado e automaticamente.
E esses mesmos registros misteriosos III / IV - em termos de capacidade, eles estão quase acumulando, mas são controlados muito, muito mal pelo teclado.
Além disso, os registros III / IV têm seu próprio mecanismo de conexão, independente da acumulação de registros. Na verdade, esse sistema permaneceu em um dos modelos mais primitivos de Ascot, que, além dos registros I, II, III, IV e K, não tinham nada - mas por que os deixaram?
Eu acho que eles deveriam ser exatamente como registros de mudança para bit. Porque é o suficiente para acoplá-los a uma série de engrenagens diagonais e obteremos um dispositivo de mudança: escreva, digamos, no número III e obtenha-o no IV, mas deslocou para a esquerda para a descarga.
Eu imagino algo assim:
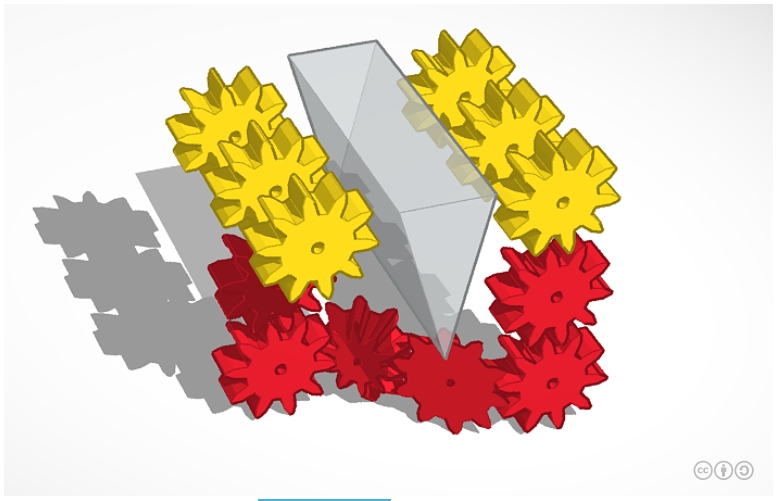Aqui você pode girar o modelo 3D.E aqui - para ver como os contadores parecem vivos.Na figura - engrenagens amarelas - os contadores III e IV (por exemplo, a primeira descarga III-1 e a segunda descarga IV-2 estão conectadas às vermelhas). Cunha translúcida - detalhes do dispositivo do contador.
As marchas vermelhas são o mesmo sistema de marchas em falta que gira a marcha III-1 ao girar a IV-2 e vice-versa. Se você montar esse sistema, para uma mudança para a esquerda, basta escrever o número desejado em IV e lê-lo em III.
A dificuldade é que, ao trabalhar, as marchas dos contadores não apenas giram, mas também se movem para cima e para baixo (aproximadamente até o raio), e o mecanismo deve suportar esse movimento. Acabou sendo um design bastante complicado, no qual não consigo pensar.
Seria ótimo se alguém que soubesse projetar melhor do que eu, por uma quantia razoável de dinheiro, criar esse sistema para imprimir em uma impressora ou fabricá-lo em hardware - com esclarecimentos e sugestões, novamente, escreva nos comentários, no PM ou envie-me [a] alple.net.
Você pode encontrar mais detalhes no meu site, na
seção sobre Ascot .