Olá Habr!
Esta publicação me pareceu interessante: obtemos
taxas de câmbio absolutas a partir de taxas de câmbio cruzadas e eu queria testar a capacidade de encontrar essa taxa de câmbio absoluta por meio de modelagem numérica, geralmente abandonando a álgebra linear.
Os resultados foram interessantes.
O experimento será pequeno: 4 moedas, 6 pares de moedas. Para cada par, uma medição de curso.
Então vamos começar
A hipótese é que o valor de qualquer moeda pode ser expresso como um valor que levará em conta o valor de outras moedas nas quais é cotado, enquanto outras moedas serão expressas no valor de todas as outras moedas. Esta é uma tarefa recursiva interessante.
Existem 4 moedas:
Para eles, os pares de moedas foram discados:
- eurusd
- gbpusd
- eurchf
- eurgbp
- gbpchf
- usdchf
Observe que, se o número de moedas for n = 4, o número de pares será k = (n ^ 2 - n) / 2 = 6. Não faz sentido procurar usdeur se eurusd for citado ...
No momento t, a taxa de câmbio de um dos provedores foi medida:
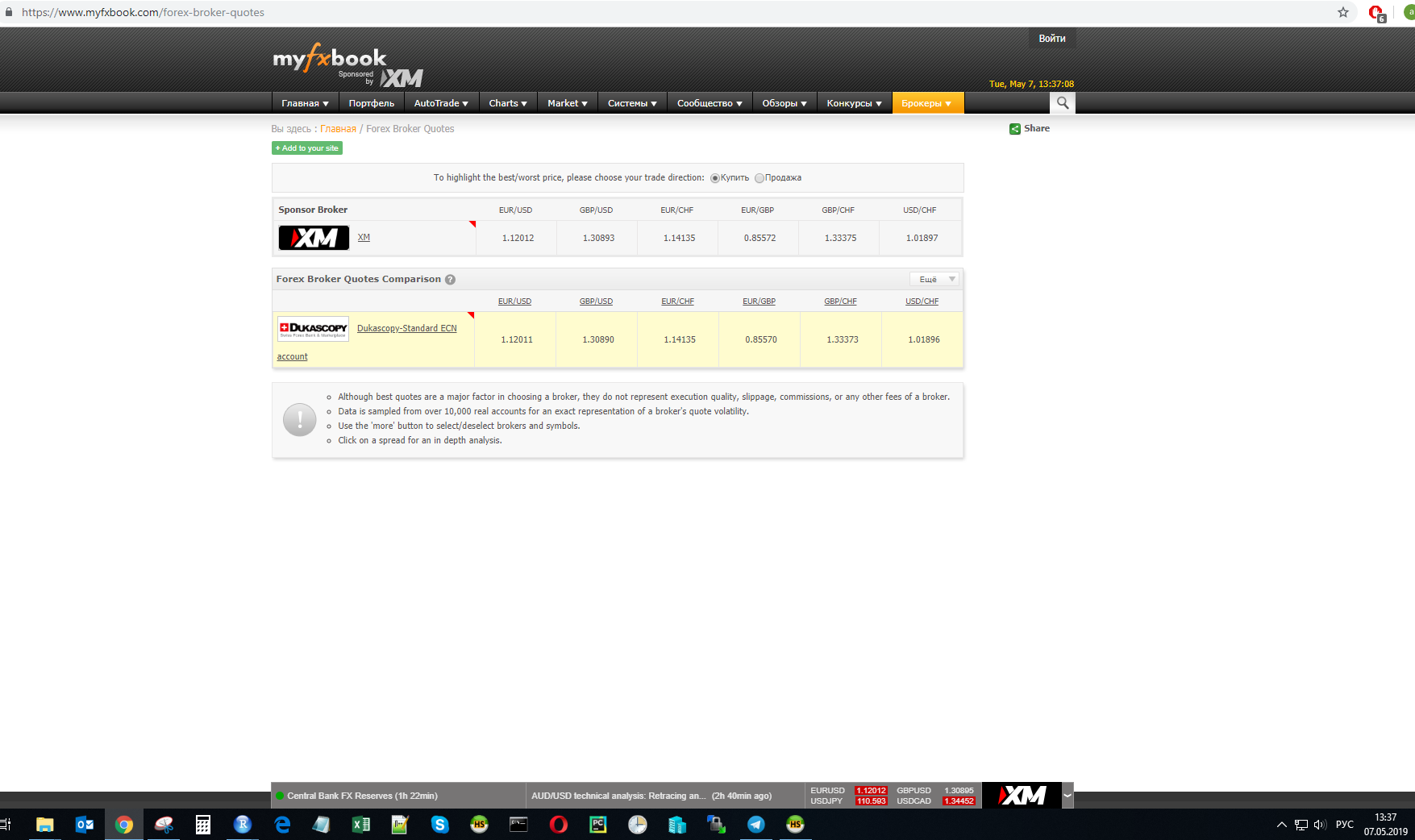
Os cálculos serão realizados para esses valores.
Matemática
Eu resolvo o problema tomando analiticamente o gradiente da função de perda, que é essencialmente um sistema de equações.
O código da experiência estará em R:
R permite usar stats :: D para obter uma derivada de uma função. Por exemplo, se queremos diferenciar pela moeda USD, obtemos a expressão:
2 * (eur / usd ^ 2 * (eurusd - eur / usd)) + 2 * (gbp / usd ^ 2 * (gbpusd -
gbp / usd)) - 2 * (1 / chf * (usdchf - usd / chf))
Para reduzir o valor da função express, realizaremos a descida do gradiente e fica imediatamente claro (vemos diferenças quadradas) que o valor mínimo será zero, que é o que precisamos.
-deriv_vals * lr
O passo de descida do gradiente será controlado pelo parâmetro lr e tudo isso é tomado com um sinal negativo.
Ou seja, em palavras humanas, selecionamos as taxas de 4 moedas para que todos os pares de moedas no experimento recebam valores iguais aos valores iniciais desses pares. Mmm, vamos resolver o quebra-cabeça - na testa!
Resultados
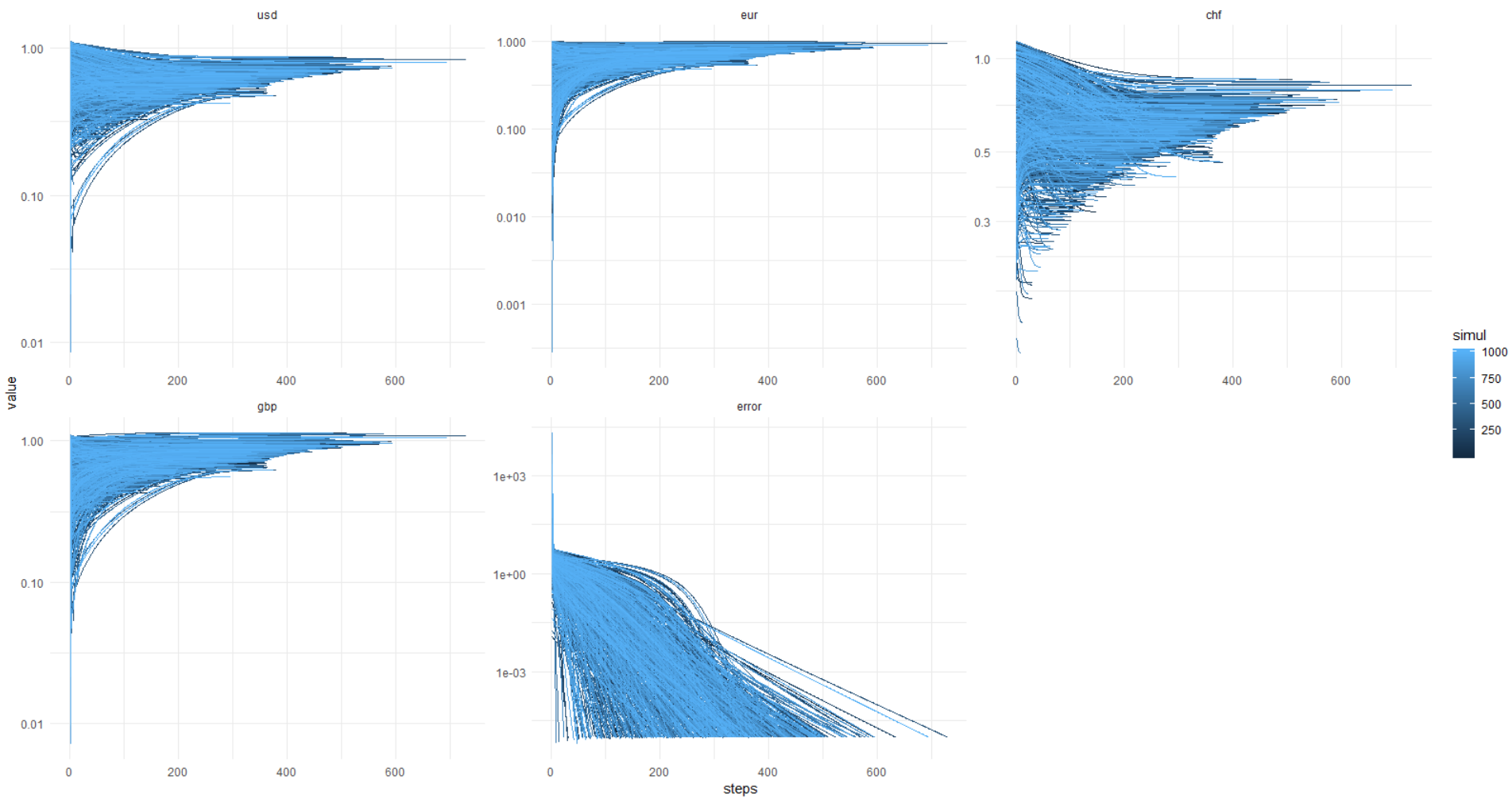
Para não esticar, informarei imediatamente o seguinte: o experimento como um todo foi bem-sucedido, o código funcionou, o erro foi próximo, próximo de zero. Mas então eu notei que os resultados são sempre diferentes.
Uma pergunta para os conhecedores: parece que esta tarefa tem um número ilimitado de soluções, mas nisto sou um zero completo, acho que eles me dirão nos comentários.
Para verificar a (des) estabilidade da solução, simulei 1000 vezes sem fixar a semente PRNG para os valores iniciais dos valores da moeda.
E aqui vem a imagem do kata: o erro chega a 0,00001 e menos (a otimização é definida dessa maneira) sempre, enquanto os valores das moedas flutuam no diabo, sabe onde. Acontece que sempre há uma decisão diferente, senhores!
Mais uma vez, esta imagem, eixo y nas unidades originais (não registradas):
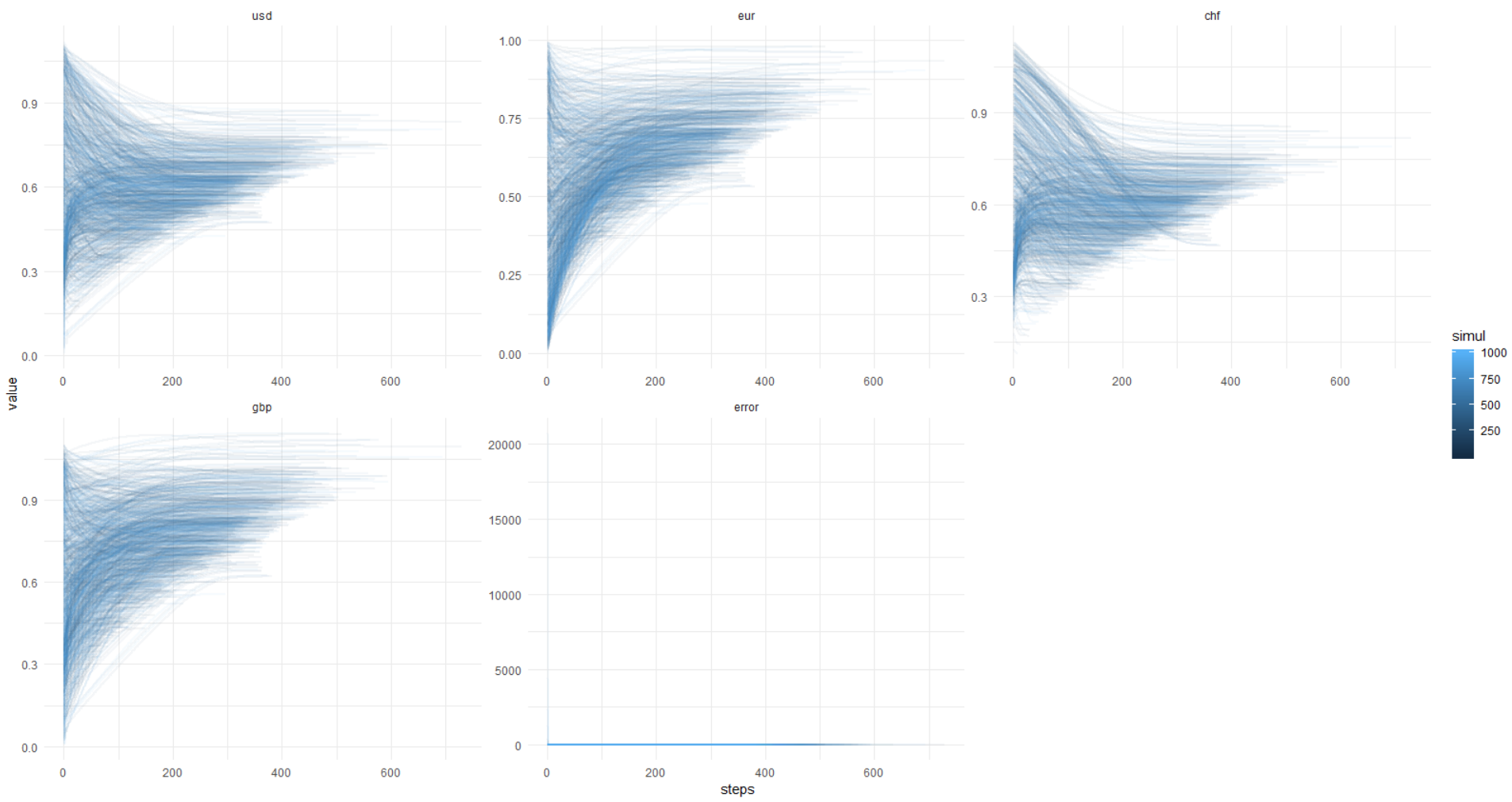
Para que você possa repetir isso, abaixo estou anexando o código completo.
O código para 1000 simulações funciona por cerca de um minuto.Conclusão
Aqui está o que ainda não está claro para mim:
- É possível estabilizar a solução de uma maneira matemática complicada;
- se haverá uma convergência com mais moedas e pares de moedas;
- se não houver estabilidade, para cada novo instantâneo de dados, nossas moedas seguirão como desejarem, se você não corrigir a semente PRNG, e isso é uma falha.
A idéia toda parece muito vaga na ausência de quaisquer pré-requisitos e limitações inteligíveis. Mas foi interessante!
Bem, eu também queria dizer que você pode ficar sem o OLS quando os dados são complicados, as matrizes são singulares, bem, ou quando a teoria é pouco conhecida (ehh ...).
Obrigado
eavprog pela mensagem inicial.
Tchau!