Prefácio

Além do meu artigo recente, também gostaria de falar sobre o tópico MU ( M ulti U ser) MIMO. Já mencionei um artigo muito famoso do professor Haardt, onde, juntamente com seus colegas, ele propõe um algoritmo para separar usuários em um Down Link com base em métodos lineares, a saber, Diagonalização de Blocos de um canal. O artigo tem um número impressionante de citações e também é a publicação fundamental para uma das tarefas do exame. Portanto, por que não fazer o básico do algoritmo proposto?

Declaração do problema

Primeiro, vamos decidir em qual área do tema MIMO trabalharemos agora.
Convencionalmente, todos os métodos de transferência dentro da estrutura da tecnologia MIMO podem ser divididos em dois grupos principais:

• Diversidade espacial

O objetivo principal é aumentar a imunidade a ruídos da transmissão. Os canais espaciais, se simplificados, duplicam-se, devido aos quais obtemos a melhor qualidade de transmissão.

Exemplos:
- Códigos de bloco (por exemplo, o esquema Alamuti );
- Códigos baseados no algoritmo Viterbi.

• Multiplexação espacial

O objetivo principal é aumentar a velocidade de transmissão. Já discutimos em um artigo anterior que, sob certas condições, o canal MIMO pode ser considerado como uma série de canais SISO paralelos. Na verdade, essa é a idéia central da multiplexação espacial: atingir o número máximo de fluxos de informações independentes. O principal problema nesse caso é a supressão da interferência entre canais (interferência entre canais) , para a qual existem várias classes de soluções:

- separação horizontal de canais;
- vertical (por exemplo, o algoritmo V-BLAST);
- diagonal (por exemplo, o algoritmo D-BLAST).

Mas isso, é claro, não é tudo.

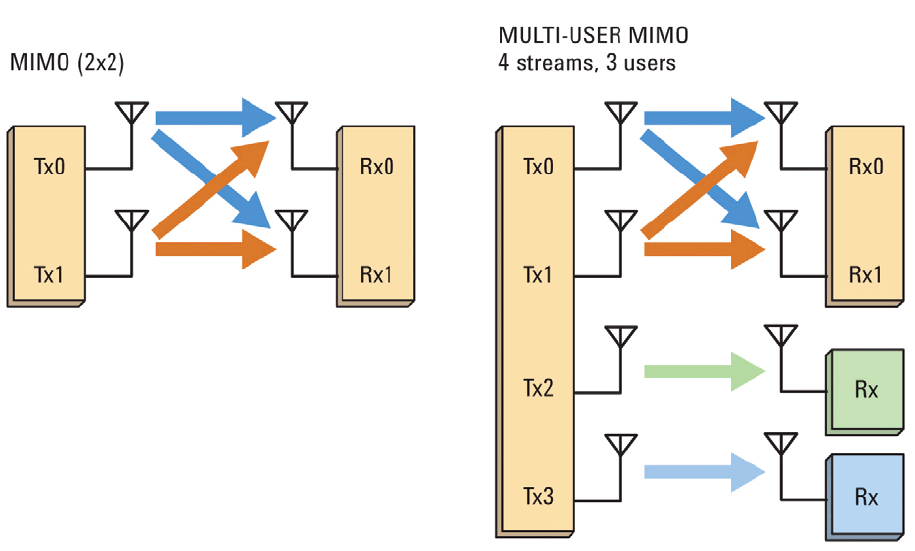
A idéia de multiplexação espacial pode ser expandida: dividir não apenas canais, mas também usuários (SDMA - Acesso Múltiplo por Divisão Espacial).

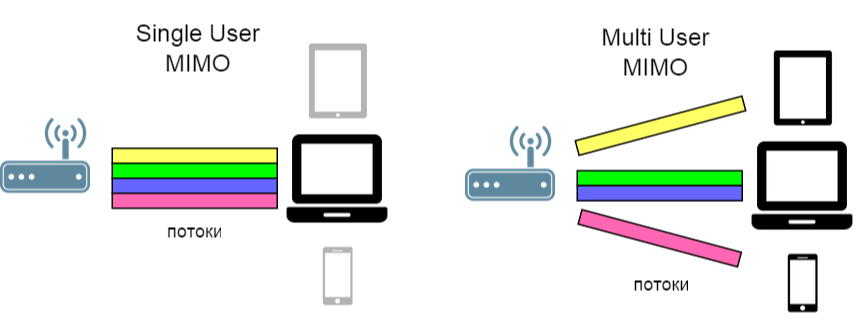
( link para fonte da ilustração )

Consequentemente, neste caso, já é necessário lutar contra a interferência entre usuários . Para isso, foi proposto um algoritmo chamado Diagonalização em Bloco de Forçar Zero , que estamos considerando hoje.

Descrição matemática

Vamos começar, como antes, com o modelo de sinal recebido. Mais precisamente, mostramos no diagrama de onde e o que vem:

A matriz do canal, neste caso, tem a forma:

com o número total de antenas de transmissão , e o número total de antenas receptoras .

Importante :
Este algoritmo pode ser aplicado apenas desde que o número de antenas de transmissão seja maior ou igual ao número total de antenas de recebimento:

Essa condição afeta diretamente as propriedades da diagonalização.

Portanto, o modelo de símbolos recebidos (sinais) pode ser escrito em forma de vetor como:

No entanto, é mais interessante analisar a fórmula para um usuário específico:

De fato:

• É um sinal útil para o k-ésimo usuário,

  
  

• - isto é interferência de outros usuários,

  
  

• - ruído aditivo.

Então chegamos à formulação da tarefa principal:

Você pode encontrar essas matrizes para que a parte de interferência chegue a zero!

É isso que faremos.

Descrição do algoritmo

Iremos executar a descrição com um exemplo e, como ilustração, darei screenshots em primeira mão , comentando um pouco sobre eles.

Considere o primeiro usuário:

Vamos falar sobre as principais etapas:

• Nós fazemos alguma matriz das matrizes de canal de todos os outros usuários.

• Nós a decompomos usando o método SVD .

  
  

• Na matriz encontramos o subespaço de ruído (subespaço nulo) - a matriz (ou seja, tudo o que vai além da classificação da matriz - denotá-lo )

  
  

• Nós compomos a partir dessa matriz de ruído e sua conjugação hermitiana, alguma matriz de projeção .

  
  

Vá em frente:

• Agora a parte original da matriz do canal multiplicar com a matriz de projeção resultante .

  
  

• Nós decompomos o resultado através de SVD.

  
  

• Na matriz escolher linhas onde - classificação .

  
  

• Transponha-os e obtenha a matriz (ou - onde indicado).

  
  

E, portanto, este procedimento será repetido para cada usuário. Não é essa a mágica da matemática: usando os métodos da álgebra linear, resolvemos problemas completamente técnicos!

Observe que, na prática, não apenas as matrizes de pré-codificação obtidas são usadas, mas também as matrizes de pós-processamento e a matriz de valores singulares (ver slides ). Este último, por exemplo, para equilibrar a potência de acordo com o já conhecido algoritmo de vazamento de água .

Modelamos o algoritmo

Eu acho que não será supérfluo realizar uma pequena simulação para consolidar o resultado. Para fazer isso, usaremos o Python 3, a saber:

import numpy as np 

para cálculos básicos e:

 import pandas as pd 

para exibir o resultado.

 class ZeroForcingBD: def __init__(self, H, Mrs_arr): Mr, Mt = np.shape(H) self.Mr = Mr self.Mt = Mt self.H = H self.Mrs_arr = Mrs_arr def __routines(self, H, mr, shift): # used in self.process() - See example above for illustration # inputs: # H - the whole channel matrix # mr - number of receive antennas of the i-th user # shift - how much receive antennas were considered before # outputs: # Uidx, Sigmaidx, Vhidx - SVD decomposition of the H_iP_i # d - rank of the hat H_i # Hidx - H_i (channel matrix for the i-th user) # r - rank of the H_i Hidx = H[0+shift:mr+shift,:] # H_i (channel matrix for the i-th user) r = np.linalg.matrix_rank(Hidx) # rank of the H_i del_idx = [i for i in range(0+shift, mr+shift, 1)] # row indeces of H_i in H H_hat_idx = np.delete(H, del_idx, 0) # hat H_i d = np.linalg.matrix_rank(H_hat_idx) # rank of the hat H_i U, Sigma, Vh = np.linalg.svd(H_hat_idx) # SVD Vhn = Vh[d:, :] # null-subspace of V^H Vn = np.matrix(Vhn).H # null-subspace of V Pidx = np.dot(Vn, np.matrix(Vn).H) # projection matrix Uidx, Sigmaidx, Vhidx = np.linalg.svd(np.dot(Hidx, Pidx)) # SVD of H_iP_i return Uidx, Sigmaidx, Vhidx, d, Hidx, r def process(self): # used in self.obtain_matrices() # outputs: # F - whole filtering (pre-coding) matrix (array of arrays) # D - whole demodulator (post-processing) matrix (array of arrays) # H - the whole channel matrix (array of arrays) shift = 0 H = self.H F = [] D = [] Hs = [] for mr in self.Mrs_arr: Uidx, Sigmaidx, Vhidx, d, Hidx, r = self.__routines(H, mr, shift) Vhidx1 = Vhidx[:r,:] # signal subspace Fidx = np.matrix(Vhidx1).H F.append(Fidx) D.append(Uidx) Hs.append(Hidx) shift = shift + mr return F, D, Hs def obtain_matrices(self): # used to obtain pre-coding and post-processing matrices # outputs: # FF - whole filtering (pre-coding) matrix # DD - whole demodulator (post-processing) matrix (array of arrays) F, D, Hs = self.process() FF = np.hstack(F) # Home Task: calculation of the demodulator matrices :) return FF 

Suponha que tenhamos 8 antenas de transmissão e 3 usuários com 3, 2 e 3 antenas de recebimento, respectivamente:

 Mrs_arr = [3,2,3] # 1st user have 3 receive antennas, 2nd user - 2 receive antennas, 3d user - 3 receive antennas Mr = sum(Mrs_arr) # total number of the receive antennas Mt = 8 # total number of the transmitt antennas H = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2); #Rayleigh flat faded channel matrix (MrxMt) 

Inicializamos nossa classe e aplicamos os métodos apropriados:

 BD = ZeroForcingBD(H, Mrs_arr) F, D, Hs = BD.process() FF = BD.obtain_matrices() 

Trazemos para uma forma legível:

 df = pd.DataFrame(np.dot(H, FF)) df[abs(df).lt(1e-14)] = 0 

E vamos dar uma pequena subida para maior clareza (embora você possa sem ela):

 print(pd.DataFrame(np.round(np.real(df),100))) 

Você deve obter algo como isto:

Na verdade, aqui estão eles, aqui está, e diagonalização. E minimizando interferências.

Essas coisas.

Literatura

1. Spencer, Quentin H., A. Lee Swindlehurst e Martin Haardt. "Métodos de força zero para multiplexação espacial de downlink em canais MIMO multiusuário." Transações IEEE no processamento de sinais 52.2 (2004): 461-471.
2. Martin Haard " Processamento robusto de transmissão para sistemas MIMO multiusuários "

PS

Aos professores e à fraternidade estudantil da minha profissão nativa , digo olá!