Por muitos anos, tenho ministrado cursos de combinatória e gráficos para estudantes de matemática e cientistas da computação (como é o russo, cientistas da computação?), Anteriormente na Universidade Acadêmica e agora na
Universidade Estadual de São Petersburgo . Nosso programa foi desenvolvido para que esses tópicos sejam mantidos como parte da "ciência da computação teórica" (outros tópicos são algoritmos, complexidade, linguagens e gramáticas). Não posso dizer o quão metafísica ou historicamente justificada: no entanto, objetos combinatórios (gráficos, sistemas de conjuntos, permutações, figuras quadriculadas etc.) começaram a ser estudados muito antes do advento dos computadores, e agora este último, embora importante, está longe de ser o único motivo de interesse em ele. Mas olhar para os próprios especialistas em combinatória e ciência da computação teórica é surpreendentemente frequentemente as mesmas pessoas: Lovas, Alon, Semeredi, Razborov e além. Provavelmente existem razões para isso. Nas minhas lições, os campeões de programação olímpica geralmente oferecem soluções não triviais para problemas complexos (não os listo, qualquer pessoa curiosa para ver as principais forças de código.) Em geral, acho que algumas coisas da combinatória podem ser de interesse para a comunidade. Fale se algo é assim ou não.
É necessário criar uma permutação aleatória de números de 1 a
$ inline $ n $ inline $ de modo que todas as permutações sejam igualmente prováveis. Isso pode ser feito de várias maneiras: por exemplo, primeiro selecione aleatoriamente o primeiro elemento, depois o segundo restante e assim por diante. Ou você pode fazer o contrário: selecione pontos aleatoriamente
$ inline $ t_1, t_2, \ ldots, t_n $ inline $ no segmento
$ inline $ [0,1] $ inline $ e veja como eles são solicitados. Substituindo o menor dos números por 1, o segundo por 2 e assim por diante, obtemos uma permutação aleatória. É fácil ver que tudo
$ inline $ n! $ inline $ permutações são igualmente prováveis. É possível e não no segmento
$ inline $ 0,1 $ inline $ escolha pontos e, por exemplo, entre números de 1 a
$ inline $ n $ inline $ . As coincidências são possíveis aqui (para um segmento, elas também são possíveis, mas com probabilidade zero, para que não nos incomodem) - você pode lidar com elas de maneiras diferentes, por exemplo, reordenando adicionalmente os números coincidentes. Ou tome
N maior para que a probabilidade de coincidência seja pequena (o caso quando
$ inline $ N = 365 $ inline $ e
$ inline $ n $ inline $ existe o número de alunos em sua turma e estamos falando da coincidência de dois aniversários.) Uma variação desse método: observe aleatoriamente
$ inline $ n $ inline $ pontos em um quadrado de unidade e veja como suas ordenadas são ordenadas em relação às abscissas. Outra variação: marca no segmento
$ inline $ n-1 $ inline $ aponte e veja como os comprimentos dos segmentos nos quais está dividido são ordenados. O ponto chave nessas abordagens é a independência dos testes, de acordo com os resultados dos quais é construído um rearranjo aleatório. Andrei Nikolaevich Kolmogorov disse que a teoria da probabilidade é uma teoria da medida mais independência - e isso será confirmado por qualquer um que tenha lidado com a probabilidade.
Vou mostrar como isso ajuda, usando o exemplo da
fórmula de ganchos para árvores :
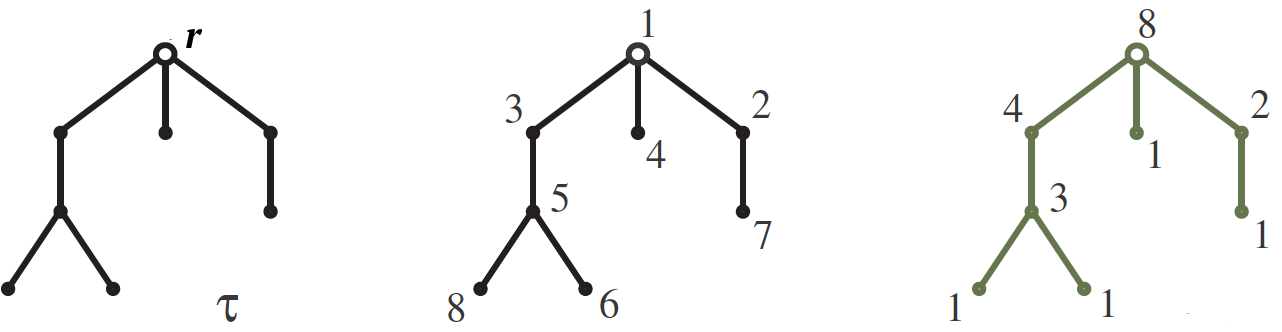
Vamos
$ inline $ \ tau $ inline $ - suspenso pela raiz
$ inline $ r $ inline $ árvore com
$ inline $ n $ inline $ picos crescendo como na foto. Nosso objetivo é calcular o número
$ inline $ S (\ tau) $ inline $
numeração de copas de árvores
$ inline $ \ tau $ inline $ números de 1 a
$ inline $ n $ inline $ de modo que, para cada aresta, o número na parte superior seja maior que na parte inferior. Um desses números é mostrado na figura do meio. A resposta é formulada usando
tamanhos de gancho . Hook
$ inline $ H (v) $ inline $ picos
$ inline $ v $ inline $ vamos chamar uma subárvore crescendo a partir desse vértice, e seu tamanho é simplesmente o número de vértices nele. Os comprimentos dos ganchos estão escritos na figura à direita, ao lado dos vértices correspondentes. Então, o número de números é
$ inline $ n! $ inline $ dividido pelo produto de tamanhos de gancho, portanto, para o nosso exemplo
$$ exibir $$ S (\ tau) = \, \ frac {8!} {8 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1 \ cdot 1 \ cdot 1 \ cdot 1} = 210. $$ exibir $ $
Podemos provar essa fórmula de maneiras diferentes, por exemplo, por indução no número de vértices, mas nossa visão de permutações aleatórias nos permite realizar a prova sem qualquer cálculo. É melhor não apenas pela elegância, mas também pelo fato de generalizar bem para questões mais sutis sobre a numeração com as desigualdades prescritas, mas não sobre isso agora. Portanto, pegue
n números reais diferentes e coloque-os aleatoriamente no topo da árvore, cada um com um número, todos
$ inline $ n! $ inline $ permutações são igualmente prováveis. Qual é a probabilidade de que, para cada aresta, o número no vértice superior da aresta seja maior que o número no seu vértice inferior? A resposta é:
$ inline $ S (\ tau) / n! $ inline $ e não depende de um conjunto de números. E, se não depender, vamos considerar os números também selecionados aleatoriamente - por definição, no intervalo
$ inline $ [0,1] $ inline $ . Em vez de selecionar números aleatoriamente primeiro e depois organizá-los aleatoriamente no topo da árvore, podemos simplesmente selecionar aleatoriamente e independentemente um número em cada vértice: seu rearranjo será aleatório automaticamente. Desta maneira
$ inline $ S (\ tau) / n! $ inline $ esta é a probabilidade de que, para números independentes aleatórios
$ inline $ \ xi (v) $ inline $ selecionou um para cada vértice
$ inline $ v $ inline $ madeira
$ inline $ \ tau $ inline $ , todas as desigualdades da forma
$ inline $ \ xi (v)> \ xi (u) $ inline $ para todas as arestas
$ inline $ v \ u $ inline $ ,
$ inline $ v $ inline $ É o vértice superior da nervura e
$ inline $ u $ inline $ - fundo. Formulamos essas condições de forma equivalente, mas de uma maneira ligeiramente diferente: para cada vértice
$ inline $ v $ inline $ esse evento deve ocorrer - eu o designarei
$ inline $ Q (v) $ inline $ : número
$ inline $ \ xi (v) $ inline $ - o máximo entre todos os números nos vértices da subárvore de gancho
$ inline $ H (v) $ inline $ .
Note que
$ inline $ \ frac {1} {| H (v) |} $ inline $ esta é a probabilidade de um evento
$ inline $ Q (v) $ inline $ . De fato, no gancho
$ inline $ H (v) $ inline $ está disponível
$ inline $ | H (v) | $ inline $ vértices e o número máximo de ganchos é mapeado para cada um deles com igual probabilidade
$ inline $ \ frac {1} {| H (v) |} $ inline $ . Então a fórmula do gancho
$ inline $ S (\ tau) / n! = \ prod_v \ frac {1} {| H (v) |} $ inline $ pode ser formulado da seguinte forma: a probabilidade de que todos os eventos ocorram ao mesmo tempo
$ inline $ Q (v) $ inline $ é igual ao produto das probabilidades desses eventos. As razões para isso podem ser diferentes, mas a primeira que vem à mente funciona aqui: esses eventos são independentes. Para entender isso, vamos olhar, por exemplo, um evento
$ inline $ Q (r) $ inline $ (correspondente à raiz). Consiste no fato de que o número na raiz é maior que todos os outros números nos vértices, e outros eventos se relacionam com comparações entre si de números escritos não na raiz. Isso é
$ inline $ Q (r) $ inline $ em relação ao número
$ inline $ \ xi (r) $ inline $ e
conjuntos de números em outros vértices, e todos os outros eventos são da
ordem de números em vértices que não sejam a raiz. Como já discutimos, “ordem” e “multidão” são independentes, portanto o evento
$ inline $ Q (r) $ inline $ independente dos outros. Descendo a árvore, descobrimos que todos esses eventos são independentes, de onde segue o necessário.
Geralmente, a fórmula para ganchos é a fórmula para numerar não os vértices da árvore, mas as células no
diagrama de Young 
aumentando nas direções dos eixos de coordenadas, e os ganchos são mais parecidos com ganchos do que para árvores. Mas essa fórmula se mostrou mais complicada e merece um post separado.
Desde que eu tinha a propósito, não posso deixar de falar sobre o modelo de um
diagrama de Young aleatório . Diagrama jovem é uma figura de
$ inline $ n $ inline $ quadrados de unidade, os comprimentos de suas linhas aumentam de baixo para cima e os comprimentos de colunas da esquerda para a direita. Número de gráficos de área de Young
$ inline $ n $ inline $ é indicado
$ inline $ p (n) $ inline $ , essa
importante função se comporta de uma maneira interessante e incomum: por exemplo, cresce mais rápido que qualquer polinômio, mas mais lenta que qualquer expoente. Portanto, em particular, gere um diagrama Young aleatório (se quisermos todos os diagramas de área
$ inline $ n $ inline $ eram igualmente prováveis
$ inline $ 1 / p (n) $ inline $ ) não é uma questão trivial. Por exemplo, se você adicionar células uma de cada vez, escolhendo um local para adicionar aleatoriamente, gráficos diferentes terão probabilidades diferentes (portanto, a probabilidade de um gráfico de linha única será igual
$ inline $ 1/2 ^ {n-1} $ inline $ .) Acontece uma medida divertida nos diagramas, mas não uniforme. O uniforme pode ser obtido da seguinte forma. Pegue o número
$ inline $ t \ in (0,1) $ inline $ , para nossos propósitos, os números na área são mais adequados
$ inline $ 1- \ mathrm {const} / \ sqrt {n} $ inline $ . Para cada
$ inline $ k = 1,2, \ ldots $ inline $
considere a distribuição geométrica em números inteiros não negativos com média
$ inline $ t ^ k $ inline $ (ou seja, probabilidade do número
$ inline $ m = 0,1, \ ldots $ inline $ é igual a
$ inline $ t ^ {km} (1-t ^ k) $ inline $ ) Escolhemos de acordo uma variável aleatória
$ inline $ m_k $ inline $ (existem várias maneiras de organizar isso). Em geral
$ inline $ k $ inline $ provavelmente 0. Vamos examinar o diagrama de Young no qual
$ inline $ m_k $ inline $ linhas são compridas
$ inline $ k $ inline $ a cada
$ inline $ k = 1,2, \ ldots $ inline $ . Eu chamo isso de
método de envio, porque a área total
às vezes é igual a
$ inline $ n $ inline $ . Se não for igual, repita o experimento. Realmente igual
$ inline $ n $ inline $ ela muitas vezes se escolher com inteligência
$ inline $ t \ in (0,1) $ inline $ . Convido o leitor a provar independentemente que todos os diagramas de uma determinada área são igualmente prováveis e estimar o número de etapas.