29 de março de 2019 - Michael Trott, pesquisador principal
Entrada
No chamado “novo SI” - uma
versão atualizada do Sistema Internacional de Unidades , que determinará sete unidades básicas de medida (segundo, metro, quilograma, ampère, kelvin, toupeira e candela) e que entrará em vigor em 20 de maio de 2019, todas as unidades do SI serão determinado através dos valores exatos das constantes físicas fundamentais. Como resultado, todas as unidades SI acima (Newton, Volt, Ohm, Pascal, etc.) serão finalmente expressas em termos de constantes fundamentais. (Finalmente, a física fundamental controlará literalmente nossas vidas diárias)
A tabela abaixo mostra como tudo vai mudar de segunda à noite 20 de maio a terça-feira de manhã 21 de maio deste ano.
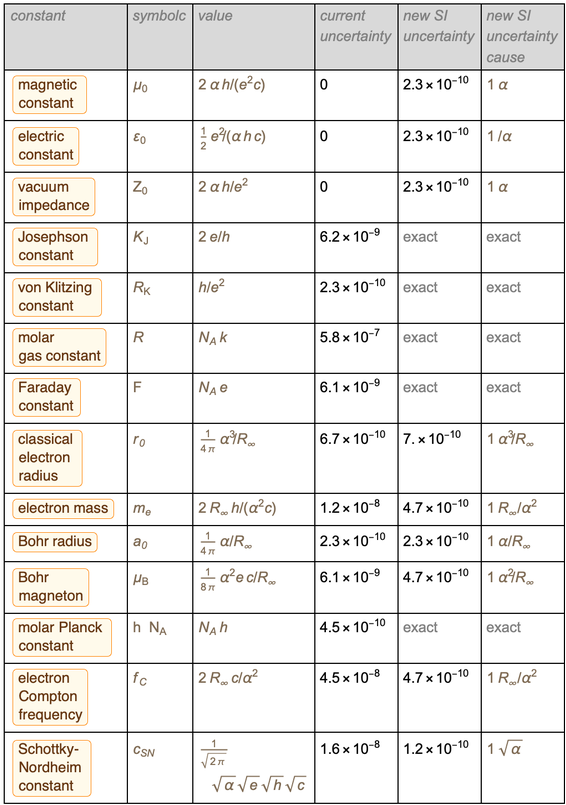
A computação dos dados desta tabela é o objetivo deste blog. Então, vamos começar com uma breve visão geral do que mudará no novo SI.
Além do conhecido valor exato da velocidade da luz, em quatro semanas outras quatro constantes físicas - a constante de Planck, a constante de Boltzmann, a constante de Avogadro e a constante de Millikan (geralmente chamada de carga elétrica elementar) - terão valores exatos. A decisão sobre essa mudança foi tomada internacionalmente em novembro do ano passado (escrevi sobre isso na minha última
blog).
Abaixo está um trecho da página 12 do rascunho do
folheto do SI atual.
Observe que nessas definições, os números decimais são entendidos como números decimais exatos, e não, digamos, números de máquinas em um computador com precisão finita e não são números exatos. A frequência de transição na estrutura superfina dividida do Cs-133, a velocidade da luz e a "eficiência da luz" já possuem valores exatos hoje.
O mundo discute mudanças futuras
Essa alteração terá algumas consequências interessantes para outras constantes físicas: algumas constantes atualmente medidas e com erros se tornarão precisas e algumas constantes atualmente corretas terão valores aproximados com erros finitos no futuro . Essas alterações são inevitáveis para garantir a consistência geral do sistema.
A primeira edição deste ano
da Physics of the World abordou esse assunto em uma
carta ao editor de William Hough; ele escreveu:
Com a fixação de carga no elétron ( e ) e a constante de Planck ( h ), todas as unidades físicas são agora “imortalizadas em pedra”, o que é muito bom. Mas isso levanta uma questão embaraçosa. Constante de estrutura fina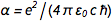 
onde c é a velocidade da luz e 
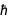é 
. De equações familiares 
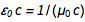e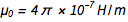 
descobrimos rapidamente que 
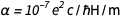. Obviamente, este é um número puro com uma quantidade adimensional e agora é fixado para sempre como igual a 1 / 137.13601, o que é muito próximo do valor aceito. Isso não é surpreendente, uma vez que o último valor seria usado nos novos valores acordados para e e ℏ . Mas a natureza tem seu próprio valor, atualmente desconhecido para nós, o qual, por causa disso, é imortalizado em diamante. Podemos ser perdoados por sugerir que sabemos melhor que a natureza. Mas e se a futura teoria do universo for aceita e der o significado exato 
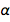Qual é significativamente diferente do valor aceito? Isso poderia acontecer? Houve tentativas de encontrar um valor teórico para α , mas incluem a eletrodinâmica quântica ameaçadora e controversa.
O problema é que, no novo sistema SI, ambos
e
agora terá valores imprecisos com algum erro. Neste blog, usaremos a Wolfram Language e seu conhecimento de unidades e constantes físicas para ver como essas e outras constantes físicas ganham (ou perdem) erros e por que essa é uma consequência matemática da definição de unidades básicas.
Uma breve visão geral dos ingredientes relevantes da Wolfram Language
A Wolfram Language é um meio exclusivo para a realização de experimentos numéricos e cálculos simbólicos, identificando possíveis consequências. Além dos recursos gerais de computação, três componentes do sistema são muito úteis aqui:
1) Unidades da Wolfram Language e estrutura de quantidades físicas.
Unidades clássicas (como metros, pés, etc.) podem ser usadas em cálculos e visualizações. E, claro, na conversão de unidades de medida.
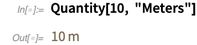
A conversão em unidades americanas comuns resulta em uma fração (em vez de um valor aproximado do número real!) Devido às proporções bem definidas das duas unidades.
Físicos (especialmente) gostam de usar unidades "naturais". Freqüentemente, essas unidades naturais são simplesmente constantes físicas ou combinações delas. Por exemplo, a velocidade da luz (a entrada em linguagem natural é usada aqui).
Expressa em unidades SI (como velocidade e unidades em metros e segundos), a velocidade da luz tem um valor preciso.
Por outro lado, a constante de Planck atualmente não possui um valor exato. Assim, seu valor, expresso em unidades base SI, é um número decimal aproximado.
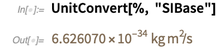
Observe que a precisão de 6.626070 ... reflete o número de números conhecidos.
Este é o último valor recomendado para a constante de Planck publicada no
CODATA 2017, em preparação para o refinamento de constantes. Abaixo está a tabela correspondente:
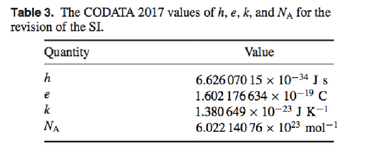
As constantes físicas (ou combinações das mesmas) que vinculam duas quantidades físicas geralmente podem ser usadas como unidades naturais. Os exemplos mais simples seriam a medição da velocidade em termos da velocidade da luz ou o torque microscópico em termos de
ℏ . Ou a energia pode ser medida em termos de massa com um fator implícito
. A função
DimensionalCombinations pode ser usada para procurar combinações de constantes físicas que permitem relacionar duas quantidades físicas. Por exemplo, as seguintes relações entre massa e energia podem ser construídas:
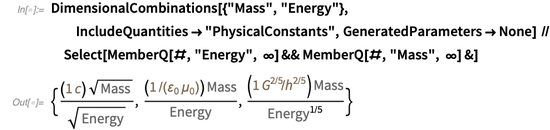
A primeira igualdade reflete a famosa fórmula de Einstein
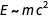
, o segundo é o equivalente da primeira relação e o terceiro - (dimensionalmente) afirma que
.
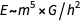
2) A classe de entidade "
PhysicalConstant " foi adicionada recentemente à
Wolfram Knowledgebase .
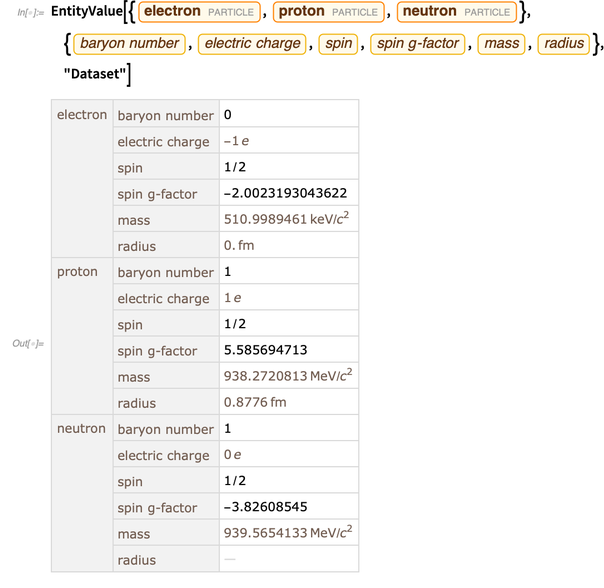
Funções e objetos na Wolfram Language “nascem computacionalmente”, ou seja, estão prontos para uso em computação. Mas para descrever e simular o mundo real, você precisa de dados sobre o mundo real. A estrutura da entidade é uma maneira conveniente e totalmente integrada de obter esses dados. Abaixo estão alguns dados sobre elétrons, prótons e nêutrons.
Uma das novas unidades de entidade são constantes físicas. Atualmente, a Base de Conhecimento contém mais de 250 constantes físicas.
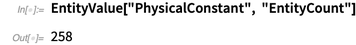
Abaixo estão uma dúzia de exemplos selecionados aleatoriamente. Além disso, sem uma definição clara de quais constantes são constantes físicas, massas de partículas fundamentais, parâmetros de Lagrange do modelo padrão etc. Por conveniência, a lista também contém
constantes astronômicas de acordo com o Almanaque Astronômico.
A maioria das constantes físicas fundamentais foram denominadas constantes de classe C. No famoso
trabalho de Jean-Marc Levy-Leblond, a seguir, são constantes das classes C e B.
Tomemos, por exemplo, a unidade natural de tempo, tempo de Planck. As
funções ToEntity e
FromEntity facilitam a
alternância entre constantes físicas como unidades e constantes físicas como entidades. Uma entidade correspondente a uma unidade de tempo de Planck é demonstrada abaixo.
A base de conhecimento possui muitas meta-informações sobre ele, por exemplo, seus valores nas últimas listas do CODATA.
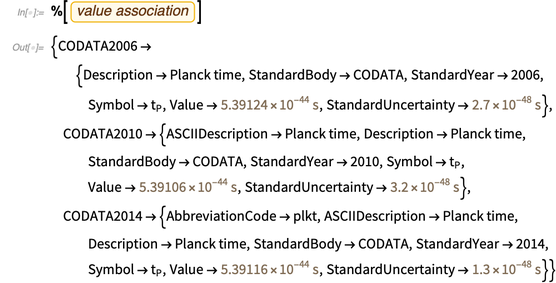
A última conclusão, que contém significado e erro, leva-nos à terceira função importante, que será útil mais tarde:
3) Introdução da função
Around [] na versão 12 da Wolfram Language. A função
Around [] fornece um valor impreciso, indicando o valor médio e o erro. O modelo aritmético
Around [] é baseado no
GUM (Guia para Expressar Erros de Medição) - não deve ser confundido com o cálculo Leibniz Plus-Minus. Aqui está um valor com um erro.
O aspecto mais importante e útil da computação com valores com erros é que eles levam em consideração as correlações. O uso ingênuo de tais valores em números ou intervalos aritméticos pode subestimar ou superestimar o erro resultante.
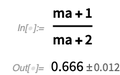
Abaixo, vemos que a função
AroundReplace [] leva em consideração a correlação.
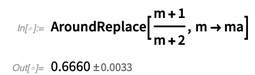
Voltar à carta ao editor
Agora vamos usar esses três componentes e a carta mais detalhada de William Hough para o editor.
Nos valores aproximados atuais de
e e
ℏ , esses dois valores para a constante de estrutura fina são consistentes dentro dos limites de seus erros. A primeira é a expressão da carta para o editor e a segunda é a quantidade (
Quantity []), que representa a constante da estrutura fina.
A cada poucos anos, o CODATA publica valores oficiais de constantes fundamentais (veja
constantes de estrutura fina ); como eu disse, os valores usados na Wolfram Language são os mais recentes valores CODATA e o erro final é refletido na precisão do número.
Observe que a constante da estrutura fina medida diretamente é um pouco mais precisa do que a que expressa a constante da estrutura fina através de outras constantes.
Se usarmos os próximos valores exatos de
e e
ℏ ,
e usarmos o valor exato atual
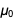
, obtemos o seguinte valor exato para a constante de estrutura fina na forma
.
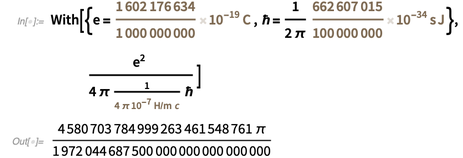
É improvável que o Senhor, que nem sequer
joga dados , escolha esse número pelo valor
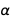
no nosso universo. Isso significa que, enquanto
e e
ℏ são fixos no novo SI, os valores exatos atuais
e
inevitavelmente “dissociar” (ver também o
artigo da Goldfarb sobre a quantidade
novo SI). (Voltaremos ao porquê
e
logo se tornem imprecisos.)
Isso significa que após 20 de maio deste ano, esses resultados serão diferentes dos apresentados abaixo.
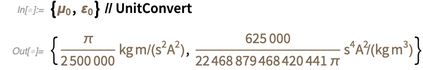
(Em uma breve nota, a classe de entidade "
PhysicalConstant " também possui valores estimados para constantes, como a constante de estrutura fina):
Agora, além do argumento teológico sobre a forma exata da constante da estrutura fina, do ponto de vista físico, por que
e
deve ser impreciso? Como argumento de probabilidade, vamos considerar
. Um dos resultados mais destacados é a lei de Coulomb.
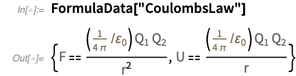
No sistema SI
existente , amperes têm uma definição "exata":
Um ampere é a corrente contínua que, se suportada em dois condutores paralelos de comprimento infinito com uma leve seção transversal redonda e colocada a uma distância de 1 metro no vácuo, criará uma força entre esses condutores igual a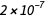 
Newton por metro de comprimento. Essa definição usa quantidades puramente mecânicas Newton e metro (ou seja, após a expansão, este é um segundo, metro e quilograma). Nenhuma relação é feita com a carga do elétron e, no sistema SI existente, a carga elementar é uma quantidade medida experimentalmente.
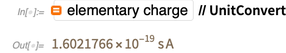
E esse valor medido experimentalmente mudou ao longo dos anos, tornando-se mais preciso.
A força no lado esquerdo da lei de Coulomb (expressa em Newtons) contém a unidade básica de quilograma que, depois que o valor da constante de Planck se torna constante, também se torna precisamente definível. Como não há razão para acreditar que todas as leis da natureza possam ser expressas em números racionais finitos, a única "parte móvel" possível na lei de Coulomb será
. Seu valor numérico deve ser determinado e fará com que os lados esquerdo e direito da lei de Coulomb coincidam.
De um ponto de vista mais fundamental da física, a constante de estrutura fina é a constante de interação, que determina a força das interações eletromagnéticas. E, talvez um dia, a física possa calcular o valor da estrutura fina constante, mas ainda estamos longe disso. Apenas escolher definições de unidade não pode fixar o valor
.
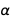
São ambos realmente
e
ficar sem correção ou é possível manter uma delas precisa? Devido à já precisa velocidade da luz e à proporção
se um dos
ou
preciso, o outro também deve ser preciso. Sabemos que pelo menos um deve ficar descomprometido; portanto, ambos devem ser descomprometidos.
Os valores que são dados agora pela constante de Planck, a constante de Boltzmann, a constante de Avogadro e a carga elementar não são arbitrários nem totalmente definidos. Eles são determinados até aproximadamente oito caracteres, portanto, as unidades de medida que determinam após 20 de maio correspondem ao "tamanho" das unidades que determinam antes de 20 de maio. Mas os números no canto inferior direito não estão definidos. Assim, o valor do valor exato futuro da carga elementar pode ser
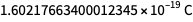
mas não
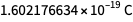
. É a navalha e a racionalidade de Occam que nos permitem usar
.
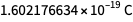
Em um nível mais técnico, a substituição no cálculo anterior foi que, através do termo
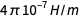
na fórmula
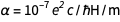foi utilizado antes da redefinição (lembre-se
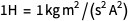
), mas também foi usado o valor exato da carga elementar, ou seja, a definição do ampere após a redefinição. E sempre precisamos permanecer em um sistema de unidades.
Cálculo da tabela de formulários otimizada por erros
Assim, surge a questão natural: quais deveriam ser esses significados "não fixos"? No meu último blog, criei manualmente um novo valor
. O que pode ser feito manualmente pode ser feito usando um programa de computador, então vamos implementar um pequeno programa que calcula a forma otimizada de erro de derivadas de constantes físicas. Em uma abordagem orientada para o futuro, uma classe de entidade de sete constantes que define um novo SI já está disponível.
Abaixo estão constantes que terão um valor exato no novo SI.
Os valores atuais dessas constantes, juntamente com seus erros (calculados usando a função
Around []), têm a forma:
Usando a classe de entidade "
PhysicalConstant ", podemos obter novos valores futuros de quantidades físicas. Observe que, como em todas as linguagens de computador, números inteiros exatos e números racionais são números inteiros explícitos ou números racionais (mas não decimais).
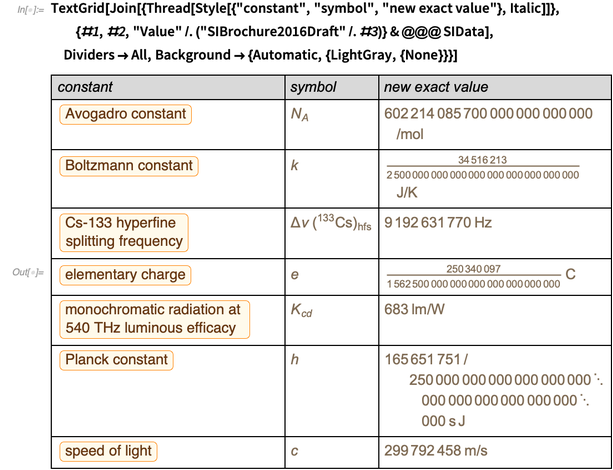
Muitas constantes físicas podem ser relacionadas por equações dadas por teorias físicas de vários campos da física. No futuro, queremos nos limitar à teoria dos fenômenos eletromagnéticos fundamentais, na qual o erro das constantes será reduzido ao erro da constante da estrutura fina
e constante de Rydberg
. Se incluíssemos, por exemplo, fenômenos gravitacionais, teríamos que usar a constante gravitacional G, que é medida independentemente, embora tenha um erro muito grande (razão pela qual a NSF teve o chamado "
Grande Desafio G ").
Além disso, nos restringimos a quantidades elétricas, magnéticas e de massa, cujos erros são reduzidos a unidades
e
.
Abaixo, usamos a nova função
Around para expressar valores com erros correspondentes
e
.
Atualmente, de acordo com o CODATA 2014, o erro relativo para
é sobre
e para
sobre
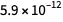
. Como você pode ver, o erro para
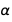
mais do que para
.
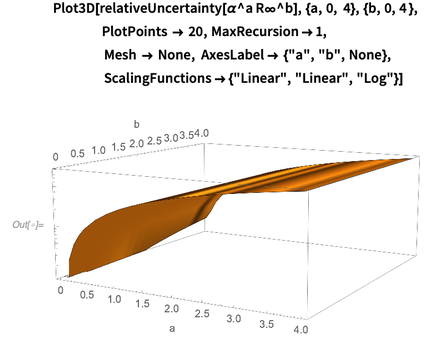
Abaixo está um gráfico do erro relativo do log-base-10
como funções
a e
b . Obviamente, em pequenos graus, o erro relativo do produto depende fracamente dos expoentes
a e
b . Este gráfico mostra que a dependência do erro
domina em relação a (expoente de estrutura fina). Essa observação é explicada pelo fato de que o erro da constante de Rydberg é 50 vezes menor que o erro da constante da estrutura fina.
Para calcular os erros de várias constantes no novo SI, usaremos as seguintes etapas:
• Recuperando representações equivalentes para constantes físicas acessíveis a partir da classe de entidade
PhysicalConstant .
Essas igualdades idênticas entre constantes físicas são as leis da física e, como tal, devem ser preservadas no antigo e no novo SI.
• Pense em fórmulas como um conjunto de igualdades algébricas às quais vários métodos de exclusão podem ser aplicados para expressar uma constante por meio de uma combinação de sete constantes básicas do novo SI, bem como constantes de estrutura fina
constantes de Rydberg
.
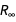
Estas são as nove constantes básicas que permitimos aplicar nas definições de cada nova constante considerada. (Tecnicamente, existem 10 constantes na lista, mas devido à simples relação de escala entre
he and, na verdade existem nove constantes "diferentes" nessa lista.)
A classe de entidade "
PhysicalConstant " contém muitas informações sobre os relacionamentos entre constantes físicas. Por exemplo, aqui estão formas equivalentes de quatro constantes que estão sendo medidas no momento e em breve serão identificadas como tendo valores precisos.
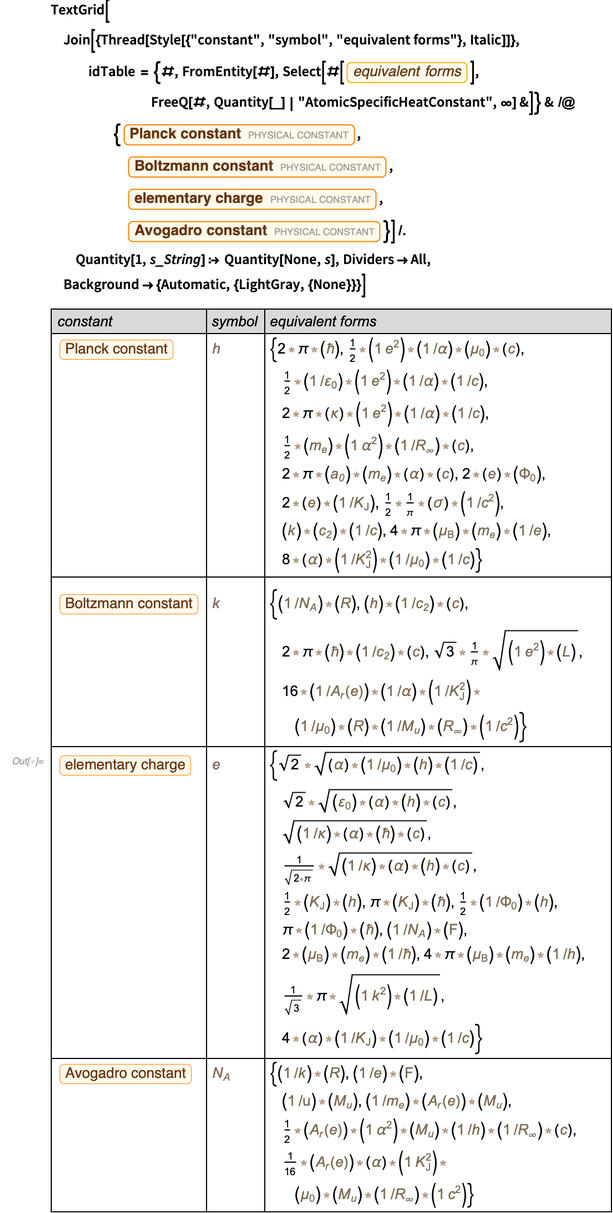
Dentro da precisão dos valores medidos, todos esses elementos da unidade funcionam agora. Aqui está uma rápida verificação numérica de formas alternativas da constante de Planck. Mas o valor numérico específico, especialmente o erro, depende da forma real da apresentação.
Around [], .
. .
, . , ? , , , , , .
, , ( ,
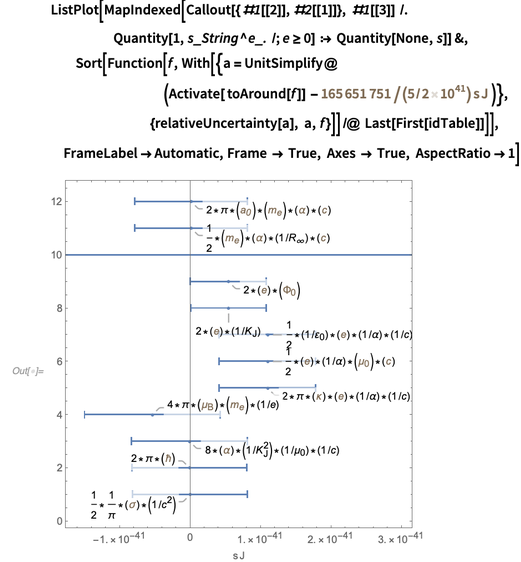
Entidade [" PhysicalConstant",. ] e em quantidade [ 1 ,. ] são equiparados). A razão pela qual usamos entidades, em vez de quantidades em cálculos subseqüentes, é dupla: primeiro, as entidades são representações convenientes e fáceis de ler; e segundo, funções algébricas (como GroebnerBasis ) não penetram quantidades para determinar a natureza de seu primeiro argumento.
Então, fazemos todas as identidades polinomiais. O último passo significa: (1) subtrair o lado esquerdo do lado direito; e (2) que não há mais poderes fracionários (por exemplo, raízes quadradas) de constantes. Realizamos essa transformação em um polinômio, procurando todos os expoentes fracionários e localizando o LCM (menor fator comum) de todos os seus denominadores.
Abaixo está uma das equações anteriores que contém constantes com uma potência fracionária.
Após polinomialização, chegamos a polinômios de várias variáveis nas três constantes presentes. Esses polinômios devem ser eliminados.
A tabela a seguir demonstra como a função
toPolynomial se aplica aos formulários equivalentes mostrados anteriormente para uma carga elementar. Após a canonização de ℏ em
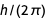
, alguns dos polinômios resultantes se tornam idênticos.
Agora, com base nas constantes físicas disponíveis (sem as constantes usadas na definição do novo SI), obtemos formas equivalentes suficientes para criar um conjunto de equações.
Abaixo está uma lista das equações polinomiais obtidas para expressar uma carga elementar.
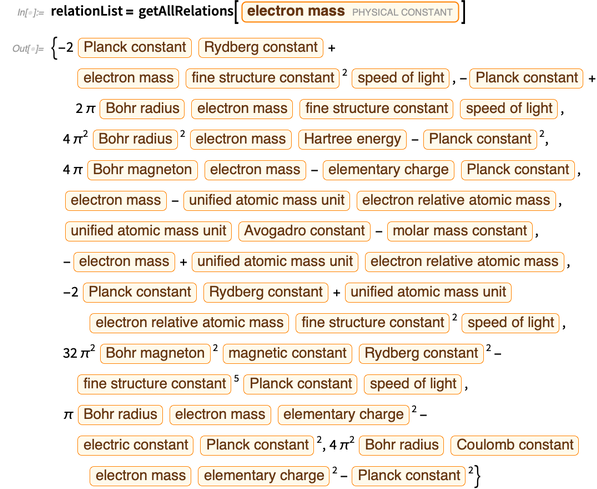
Expressamos todos os erros através dos erros
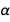
e
. Somente essas duas constantes são suficientes para expressar o erro de muitas constantes físicas. E como seus erros são independentes um do outro e como são muito pequenos, essas duas constantes bem conhecidas são mais adequadas para expressar uma nova versão otimizada (no sentido de erros) de muitas constantes físicas. E, é claro, permitimos todas as sete constantes exatas do novo SI; como são quantidades precisas, a presença deles não altera o erro.
O trabalho principal sobre a expressão de uma constante constante em termos de constantes SI e
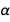
e
será implementado pela função
GroebnerBasis . Definir o
parâmetro MonomialOrder -> ElventionOrder é uma etapa crítica que remove todas as quantidades físicas "desnecessárias", deixando uma equação polinomial com constantes definidas com precisão e (se necessário) estrutura fina e constantes de Rydberg.
Ao eliminar as constantes ligadas pela massa do elétron, obtemos
.
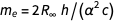
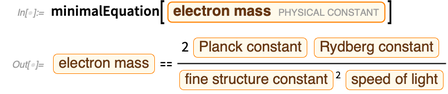
O erro desta expressão surge do termo
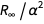
. Podemos definir uma função que remove um membro
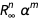
causando um erro.
Para uma representação mais compacta, podemos definir uma função que retorne uma forma equivalente, bem como erros antigos e novos - na forma de uma string.
Terminamos o blog apresentando uma tabela de erros antigos e novos para mais de uma dúzia de constantes físicas. Esta lista é selecionada como um exemplo representativo; outras constantes podem ser processadas de maneira semelhante (isso pode exigir a adição de constantes imprecisas adicionais para conservação, como a constante gravitacional ou os parâmetros do modelo padrão).
A combinação das linhas em uma tabela fornece o seguinte resultado para a representação ideal dessas constantes no novo sistema de unidades SI.
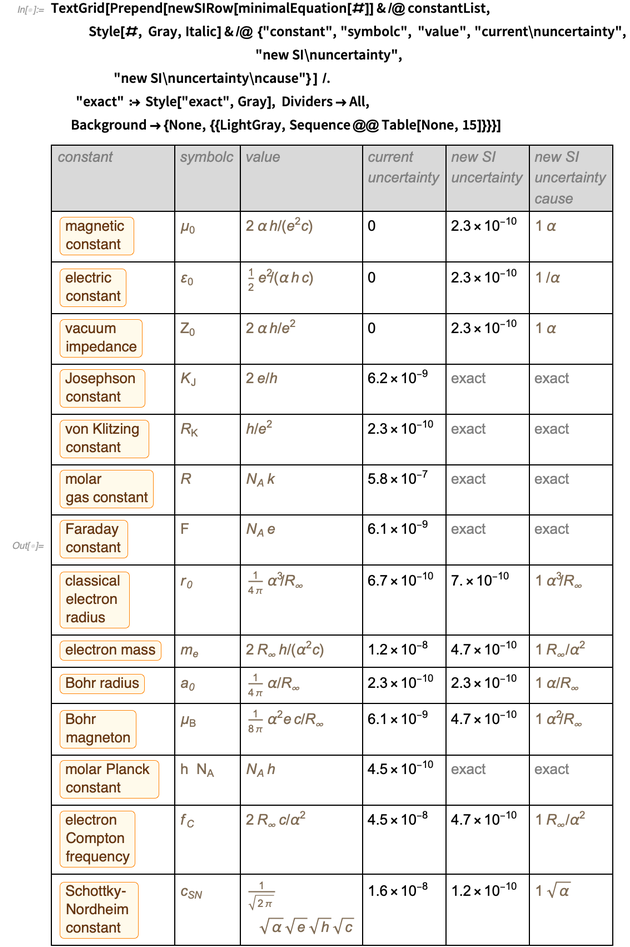
Era uma tabela que pretendíamos exibir e conseguimos exibi-la. Preste atenção à aparência
no numerador e denominador
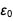
e
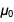
para que após a redução o resultado
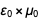
torna-se
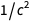
. Uma lista semelhante pode ser encontrada na parte inferior da página da Wikipedia,
redefinindo as unidades SI .
Agora podemos esperar com calma o
Dia Mundial da Metrologia de 2019 por um mundo fundamentalmente melhor, descrito através de constantes fundamentais.
Faça o download do
Wolfram Notebook Blog.
Sistema temporário Wolfram Mathematica gratuitoTem uma pergunta? Informações de contato-russia@wolfram.com