Análise da Wavelet - Parte 1

1. Introdução

Considere a transformação de wavelet discreta (DWT) implementada na biblioteca PyWavelets PyWavelets 1.0.3 . PyWavelets é um software livre e de código aberto lançado sob a licença MIT.

Ao processar dados em um computador, uma versão discreta da transformação contínua de wavelets pode ser executada, cujos princípios básicos são descritos no meu artigo anterior. No entanto, especificar valores discretos dos parâmetros (a, b) de wavelets com uma etapa arbitrária Δa e Δb requer um grande número de cálculos.

Além disso, o resultado é um número excessivo de coeficientes, excedendo em muito o número de amostras do sinal original, o que não é necessário para sua reconstrução.

A transformada de wavelet discreta (DWT) implementada na biblioteca PyWavelets fornece informações suficientes para análise de sinal e para sua síntese, além de econômica em termos de número de operações e de memória necessária.

Quando usar a transformação wavelet em vez da transformação de Fourier

A transformação de Fourier funcionará muito bem quando o espectro de frequência estiver estacionário. Nesse caso, as frequências presentes no sinal são independentes do tempo e o sinal contém as frequências xHz que estão presentes em qualquer lugar do sinal. Quanto mais instável o sinal, pior os resultados. Isso é um problema, pois a maioria dos sinais que vemos na vida real são instáveis ​​por natureza.

A transformação de Fourier tem alta resolução no domínio da frequência, mas resolução zero no domínio do tempo. Mostramos isso nos dois exemplos a seguir.



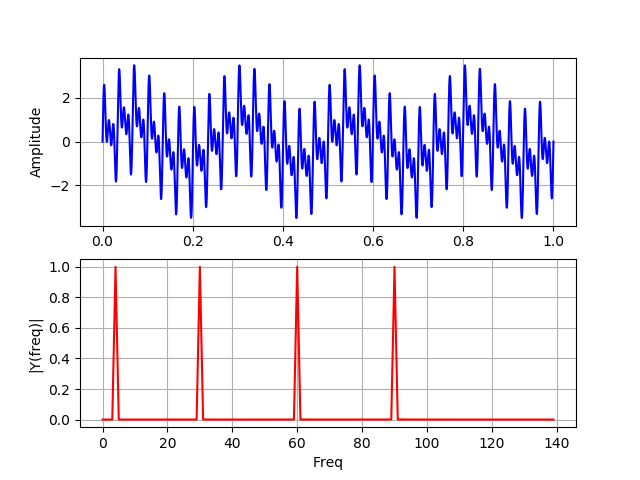
Neste gráfico, todas as quatro frequências estão presentes no sinal durante todo o tempo de sua operação.




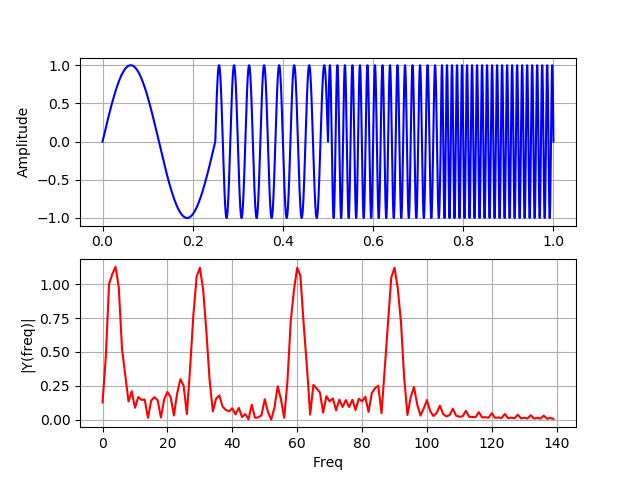
Neste gráfico, os sinais não se sobrepõem no tempo, os lobos laterais são devidos a um intervalo entre quatro frequências diferentes.

Para dois espectros de frequência contendo exatamente os mesmos quatro picos, a transformação de Fourier não pode determinar onde essas frequências estão presentes no sinal. A melhor abordagem para analisar sinais com um espectro de frequência dinâmico é a transformação wavelet.

As principais propriedades das wavelets

A escolha do tipo e, portanto, das propriedades da wavelet, depende da tarefa de análise, por exemplo, para determinar os valores efetivos das correntes no setor de energia elétrica, as wavelets da Ingrid Daubechies de maior ordem fornecem maior precisão. As propriedades da wavelet podem ser obtidas usando a função pywt.DiscreteContinuousWavelet () na seguinte listagem:


Temos:

discrete_wavelets - ['db5', 'sym5', 'coif5', 'haar']

 Wavelet db20 Family name: Daubechies Short name: db Filters length: 40 Orthogonal: True Biorthogonal: True Symmetry: asymmetric DWT: True CWT: False 

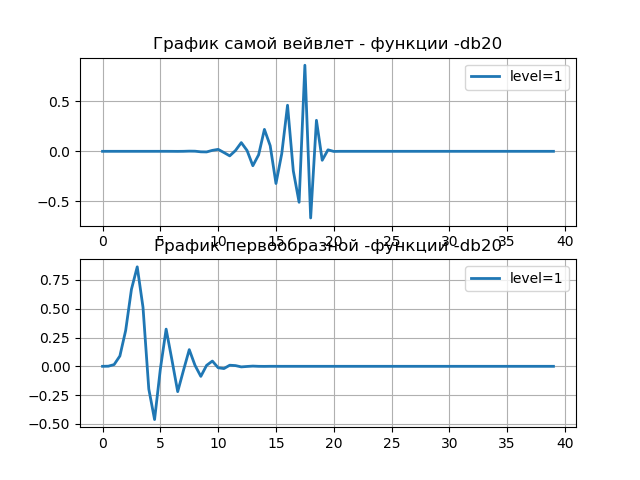
Em vários casos práticos, é necessário obter informações sobre a frequência central da wavelet psi - uma função usada, por exemplo, na análise wavelet de sinais para detectar defeitos nas engrenagens:

 import pywt f=pywt.central_frequency('haar', precision=8 ) print(f) #  : scale=1 f1=pywt.scale2frequency('haar',scale) print(f1) 

 0.9961089494163424 0.9961089494163424 

Usando a frequência central $$$f_ {c}$wavelet materna e fator de escala “a” podem converter escalas em pseudo-frequências $$$f_ {a}$usando a equação:

$$$f_ {a} = \ frac {f_ {c}} {a}$

Modos de extensão de sinal

Antes de calcular a transformada de wavelet discreta usando bancos de filtros , torna-se necessário prolongar o sinal . Dependendo do método de extrapolação, artefatos significativos podem ocorrer nos limites do sinal, levando a imprecisões na transformação DWT.

O PyWavelets fornece várias técnicas de extrapolação de sinal que podem ser usadas para minimizar esse efeito negativo. Para demonstrar esses métodos, use a seguinte listagem:




Os gráficos mostram como um sinal curto (vermelho) se expande (preto) além do seu comprimento original.

Transformada discreta de wavelet

Para demonstrar o DWT, usaremos um sinal com um espectro de frequência dinâmico, que aumenta com o tempo. O início do sinal contém valores de baixa frequência e o final do sinal contém frequências da faixa de ondas curtas. Isso nos permite determinar facilmente qual parte do espectro de frequência é filtrada simplesmente observando o eixo do tempo:




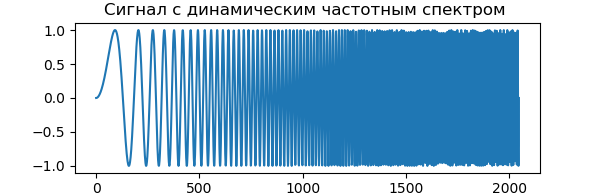
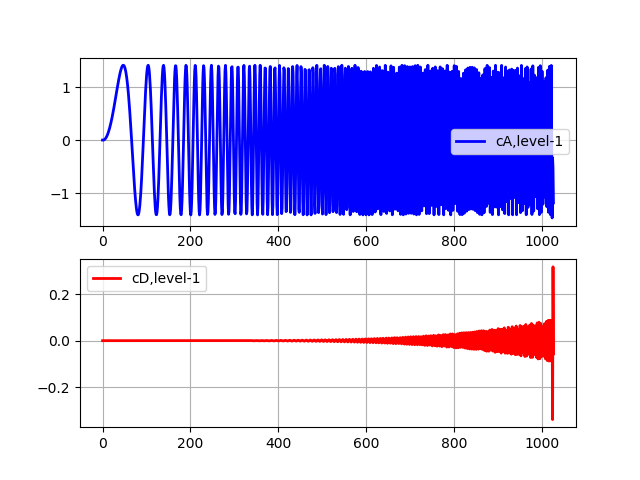
A transformação de wavelet discreta no PyWavelets 1.0.3 é a função pywt.dwt (), que calcula os coeficientes aproximados cA e os coeficientes detalhados cD da transformação de wavelet de primeiro nível do sinal especificado pelo vetor:







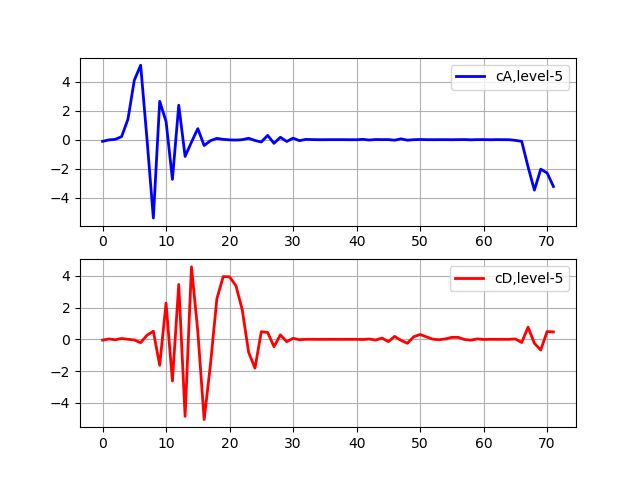
Os coeficientes de aproximação (cA) representam a saída do DWT do filtro passa-baixo (filtro de média). Os coeficientes de detalhes (cD) representam a saída do DWT do filtro passa-alto (filtro diferencial).

Você pode usar a função pywt.wavedec () para calcular imediatamente os coeficientes de nível superior. Esta função recebe o sinal e o nível de entrada como entrada e retorna um conjunto de coeficientes de aproximação (n-ésimo nível) e n conjuntos de coeficientes de detalhes (de 1 a n-ésimo nível). Aqui está um exemplo para o quinto nível:

 from pywt import wavedec from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=5) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show() 

Como resultado, obtemos os mesmos gráficos do exemplo anterior. Os coeficientes cA e cD podem ser obtidos separadamente:

Para cA:

 import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('a', data, 'db20', mode='symmetric', level=1) 

Para cD:

 import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('d', data, 'db20', mode='symmetric', level=1) 

Banco de filtro

Alguns dos problemas relacionados aos níveis de conversão foram discutidos na seção anterior. No entanto, o DWT é sempre implementado como um banco de filtros na forma de uma cascata de filtros passa-alto e passa-baixo. Os bancos de filtros são uma maneira muito eficaz de dividir um sinal em várias sub-bandas de frequência.

No primeiro estágio, em pequena escala, analisando o comportamento de alta frequência do sinal. No segundo estágio, a escala aumenta com um fator de dois (a frequência diminui com um fator de dois) e analisamos o comportamento de cerca da metade da frequência máxima. No terceiro estágio, o fator de escala é quatro e analisamos o comportamento da frequência de cerca de um quarto da frequência máxima. E isso continua até atingirmos o nível máximo de decomposição.

O nível máximo de decomposição pode ser calculado usando a função pywt.wavedec (), enquanto a decomposição e os detalhes terão a seguinte aparência:


Temos:

Nível máximo de decomposição: 7



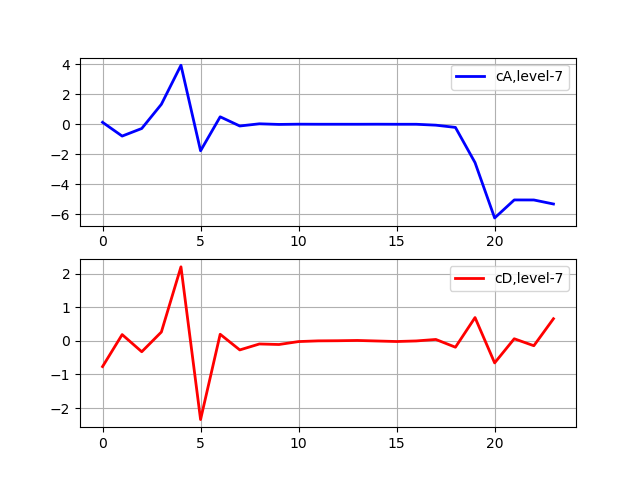
A decomposição para quando o sinal fica menor que o comprimento do filtro para uma dada wavelet sym5. Por exemplo, suponha que tenhamos um sinal com frequências de até 1000 Hz. No primeiro estágio, separamos nosso sinal em partes de baixa e alta frequência, ou seja, 0-500 Hz e 500-1000 Hz. No segundo estágio, pegamos a parte de baixa frequência e novamente a dividimos em duas partes: 0-250 Hz e 250-500 Hz. No terceiro estágio, dividimos a parte 0-250 Hz na parte 0-125 Hz e a parte 125-250 Hz. Isso continua até atingirmos o nível máximo de decomposição.

Análise de arquivos wav usando escalogramas fft de Fourier e wavelet

Para análise, use o arquivo WebSDR . Considere a análise do sinal reduzido usando triângulo de scipy.signal e a implementação da transformada discreta de Fourier em python (fft de scipy.fftpack). Se o comprimento da sequência fft não for igual a 2n, em vez da transformação rápida de Fourier (fft), será executada uma transformação discreta de Fourier (dft). É assim que essa equipe trabalha.

Usamos o buffer de transformação rápida de Fourier de acordo com o seguinte esquema (dados numéricos, por exemplo):

fftbuffer = np.zeros (15); crie um buffer preenchido com zeros;
fftbuffer [: 8] = x [7:]; mova o final do sinal para a primeira parte do buffer; fftbuffer [8:] = x [: 7] - movemos o início do sinal para a última parte do buffer; X = fft (fftbuffer) - consideramos a transformada de Fourier de um buffer preenchido com os valores do sinal.

Para tornar o espectro de fase mais legível, a implantação de fase é aplicável. Para fazer isso, altere a linha com o cálculo da característica de fase: pX = np.unwrap (np.angle (X)).




Para análise comparativa, usaremos um escalograma wavelet que pode ser construído usando a função tree = pywt.wavedec (signal, 'coif5') no matplotlib.




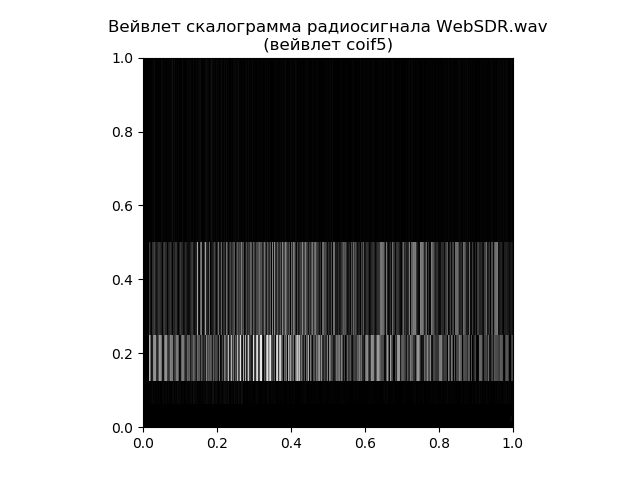
Assim, o escalograma fornece uma resposta mais detalhada à questão da distribuição de frequências ao longo do tempo, e a rápida transformação de Fourier é responsável pelas próprias frequências. Tudo depende da tarefa, mesmo para um exemplo tão simples.

Conclusões

1. A lógica para o uso de uma transformada de wavelet discreta para sinais dinâmicos é dada.
2. São fornecidos exemplos de análise de wavelets usando o PyWavelets 1.0.3, um software de código aberto gratuito lançado sob a licença MIT.
3. São consideradas ferramentas de software para uso prático da biblioteca PyWavelets.