Analisando um problema das olimpíadas, percorreremos os corredores sinuosos da geração de labirintos e sua passagem, e também veremos que na linguagem Julia a simplicidade da implementação de algoritmos limita seu pseudo-código.

Desafio

O labirinto é um quadrado quadriculado de 10 por 10, em algumas células existem obstáculos e em uma célula há uma saída. O robô está em um labirinto e pode executar 4 comandos: mover uma célula para baixo, para cima, direita ou esquerda. Se o robô tentar ir além dos limites do labirinto ou entrar na gaiola com um obstáculo, ele permanecerá no lugar. Se o robô entra na saída, sai do labirinto e ignora outros comandos. Escreva um programa para o robô, executando o qual o robô chegue à saída, independentemente da célula em que estava localizado no início. O programa deve consistir em não mais que 1000 equipes.

Formato de entrada

Não há entrada. Você precisa escrever um programa para uma condição específica especificada
o labirinto.
A versão do labirinto que você pode copiar. 0 - célula livre, 1 - obstáculo, x -
saída.

0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000 

Formato de saída

Uma linha composta por caracteres U, D, R, L de comprimento não superior a 1000

Preparação

Quem não trabalhou com gráficos em Julia precisa baixar pacotes

 using Pkg Pkg.add("Plots") Pkg.add("Colors") Pkg.add("Images") Pkg.build("Images") #     

É mais conveniente trabalhar em Jupyter, pois as imagens serão exibidas diretamente durante o trabalho. Aqui você encontra informações sobre a instalação, além de uma introdução e tarefas para iniciantes.

Na condição de nossa tarefa, há uma versão do labirinto para cópia

 S0 = "0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000" 

Para desenhar um labirinto, você precisa fazer uma matriz. Como não queremos colocar espaços manualmente, trabalharemos com a linha:

 S1 = prod(s-> s*' ', '['*S0*']') # prod(fun, arr)    arr #     fun #  julia  *   "[ 0 0 1 1 0 1 0 0 1 1 \n 0 1 0 0 0 0 1 0 0 0 \n 0 1 1 0 x 0 0 0 0 0 \n 0 0 1 0 0 0 0 1 0 0 \n 0 0 0 0 1 1 1 0 0 0 \n 0 0 0 0 1 0 0 1 0 0 \n 0 0 0 0 0 1 0 0 1 0 \n 0 1 0 0 1 0 1 0 1 0 \n 0 0 1 1 0 0 1 0 1 0 \n 1 0 0 0 0 1 1 0 0 0 ] " 

Substituindo a letra estranha x por um número e analisando a string, obtemos uma matriz inteira definindo nosso labirinto. Então, para maior comodidade, troque os para zeros e os para zeros, e coloque o labirinto na parede:

 S2 = replace(S1, 'x'=>'9') M0 = S2 |> Meta.parse |> eval m,n = size(M0) M1 = replace(M0, 1=>0, 0=>1) M = zeros(Int64,m+2,n+2) for i in 2:m+1, j in 2:n+1 M[i,j] = M1[i-1,j-1] end M # Maze map matrix 12×12 Array{Int64,2}: 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 

Na matriz

 length(M) 144 

células e a partir deles

 sum(M)-9 70 

em que você pode andar, ou seja, possíveis posições iniciais. Você pode exibir o resultado construindo um histograma bidimensional

 using Plots heatmap(M, yaxis = :flip) # flip -   

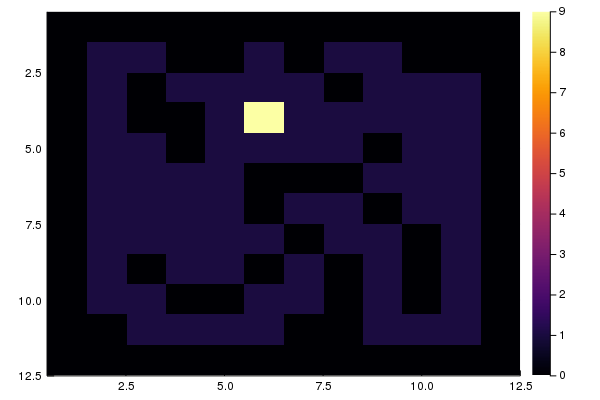
Verificação da solução

Primeiro de tudo, você precisa elaborar procedimentos que verifiquem a exatidão da solução proposta. Defina o tipo composto Point para usar a terminologia de pontos e coordenadas:

 mutable struct Point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end 

E agora você precisa aprender como converter uma sequência de comandos que sejam compreensíveis para o robô em código.

A ideia é bem simples: existe uma coordenada inicial, uma linha surge com um algoritmo que diz como andar. Pegamos uma letra e olhamos para qual das células vizinhas pisar. À coordenada atual, adicionamos o valor armazenado nesta célula. Ou seja, se houver zero (parede), não nos movemos para lugar algum; caso contrário, demos um pequeno passo na direção necessária.

Usando o poder da metaprogramação, você pode substituir a sequência de instruções recebida por um código uniforme e volumoso e executá-lo

 S = "RRLDUURULDDRDDRRRUUU" S1 = replace(S , "R"=>"c.y+=M[cx, c.y+1];") S1 = replace(S1, "L"=>"cy-=M[cx, cy-1];") S1 = replace(S1, "U"=>"c.x+=M[c.x+1, cy];") S1 = replace(S1, "D"=>"cx-=M[cx-1, cy];") #  - start point Sp = eval( Meta.parse(S1) ) 

Mas esse método tem uma série de inconvenientes, portanto, usaremos os operadores condicionais clássicos. A propósito, o fato de a saída ser indicada pelo número 9 é um pequeno truque: para não verificar cada célula e se é a saída, iniciamos o movimento adicionando o valor armazenado em uma célula específica. Quando o robô pisa na saída, um número deliberadamente grande é adicionado à sua coordenada, de forma que o robô voe além dos limites da matriz, o que pode ser detectado como um erro usando o bloco:

 try #     catch #       end 

Assim, implementamos uma função que verifica se o robô alcança a saída a partir do ponto c executando comandos a partir da string str :

 function isexit(str, c) scatter!([cy],[cx]) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end 

Vamos coletar uma função que irá percorrer todas as posições iniciais

 function test(Str) k = 0 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end 

Verifique os comandos:

 S = "RRRLDUUURRRUUURRRRLLLRRUULDDDDRRRRDDDRRRUUU" heatmap(M, yaxis = :flip) test(S) # 10 test completed from 70 plot!(legend = false) 

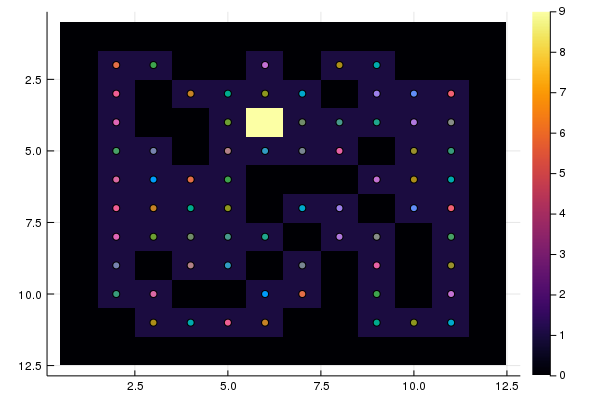
Todos os pontos de partida foram testados e apenas 10 levaram à saída. É necessário construir rotas de cada ponto até a saída.

Antes de mergulhar na geração e passagem dos labirintos, salvaremos nossos resultados. Usaremos o pacote Images.jl que oferece muitas possibilidades no campo de processamento de imagens (um bom exemplo ). Uma de suas ferramentas de suporte é o pacote Colors.jl , que expande a capacidade de Julia de trabalhar com cores.

 using Images clrs(x) = x==9 ? RGB(1.,0.5,0) : RGB(x,x,x) maze = clrs.(M) # maze = Gray.(maze) # save("D:/dat/maze12x12.png", maze) 

Pesquisa em profundidade

Implementou a ideia de um artigo no Habr .
A ideia é simples: criar uma grade de paredes

 M = 10 N = 10 A = [ i&j&1 for i in 0:N, j in 0:M ] # isodd(i) & isodd(j) & 1 Gray.(A) # from Images.jl 

depois, percorrendo o caminho, rompemos a rota e os galhos. Definimos uma função que encontra áreas vizinhas não visitadas (nós as designaremos, digamos, por um empate) e retorna um desses vizinhos (se não houver vizinhos não visitados, ele retornará um sinalizador):

 function neighbours2(A,p, n, m) nbrs = [Point(px, p.y+2), # up Point(px, py-2), # down Point(px-2, py), # left Point(p.x+2, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==2 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(-1,-1) end 

Vamos quebrar as paredes assim:

 function breakwall(A, newp,oldp) #  : x = (newp.x + oldp.x) >> 1 #   y = (newp.y + oldp.y) >> 1 A[x,y] = 1 end 

Algoritmo

1. Atualize a célula inicial e marque-a como visitada.
2. Enquanto houver células não visitadas
   1. Se a célula atual tiver "vizinhos" não visitados
   1. Empurre a célula atual para a pilha
   2. Selecione uma célula aleatória da vizinha
   3. Remova a parede entre a célula atual e a célula selecionada.
   4. Atualize a célula selecionada e marque-a como visitada.
   2. Caso contrário, se a pilha não estiver vazia
   1. Puxe a gaiola para fora da pilha
   2. Faça atual
   3. Caso contrário
   1. Selecione uma célula não visitada aleatória, atualize-a e marque-a como visitada.

 function amazeng(n, m) M = [ 2(i&j&1) for i in 0:n, j in 0:m ]; p = Point(2,2) #   lifo = [] #   push!(lifo, p) #i = 0 while length(lifo) != 0 #     M[px,py] = 1 #     np = neighbours2(M, p, n, m) # new point #    -   if np.x == np.y == -1 p = pop!(lifo) else push!(lifo, p) breakwall(M, np, p) p = np #i+=1 #maze = Gray.(M/2) #save("D:/dat/maze$i.png", maze) end end M[1,2] = 1 #  M[n,m+1] = 1 #  Gray.(M) end 

 lbrnt = amazeng(36, 48) # save("D:/dat/maze111.png", lbrnt) 

Retrocedendo o algoritmo de pesquisa de caminho:

1. Atualize a célula inicial e marque-a como visitada.
2. Até que uma solução seja encontrada
   1. Se a célula atual tiver "vizinhos" não visitados
   1. Empurre a célula atual para a pilha
   2. Selecione uma célula aleatória da vizinha
   3. Atualize a célula selecionada e marque-a como visitada.
   2. Caso contrário, se a pilha não estiver vazia
   1. Puxe a gaiola para fora da pilha
   2. Faça atual
   3. Caso contrário, não há saída.

Estamos procurando vizinhos, pelo contrário, dentro do raio de uma célula, e não através de uma:

 function neighbours1(A, p, n, m) nbrs = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==1 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(0,0) end 

Defina um algoritmo para passar o labirinto desenhando a rota e tentativas malsucedidas

 function amazeng(img, start, exit) M = Float64.(channelview(img)) n, m = size(M) p = start M[exit.x,exit.y] = 1 lifo = [] push!(lifo, p) while px != exit.x || py != exit.y M[px,py] = 0.4 np = neighbours1(M, p, n, m) if np.x == np.y == 0 M[px,py] = 0.75 p = pop!(lifo) #  -  ,    #      else push!(lifo, p) p = np end end Gray.(M) end 

Como alguns notaram, também é chamada uma função, como a que os algoritmos geram (agendamento múltiplo). Quando você o chama com dois números, ele elaborará o método de construção do labirinto, mas se você o especificar, especificando a imagem e dois pontos (as coordenadas da entrada e da saída) como argumento, na saída, obteremos uma imagem com o labirinto passado

 img0 = load("D:/dat/maze111.png") amazeng(img0) 

Vamos tentar no nosso labirinto:

 img0 = load("D:/dat/maze12x12.png") n, m = size(img0) amazeng(img0, Point(11,9), Point(4,6) ) 

Mesmo se você modificar a função para que a rota seja lembrada, o algoritmo ainda será ineficaz devido aos espaços abertos. Mas os labirintos saem ótimos.

Algoritmo aleatório de Prim

Assim que você começa a desenhar labirintos, você não para. Vamos executar outro algoritmo interessante:

• Comece com uma grade cheia de paredes.
• Selecione uma célula, marque-a como parte do labirinto. Adicione paredes celulares à lista de paredes.
• Enquanto houver paredes na lista:
  
  • Selecione uma parede aleatória da lista. Se apenas uma das duas células que o muro compartilha for visitada, então:
    
    • Faça uma passagem na parede e marque a célula não visitada como parte do labirinto.
    • Adicione paredes celulares adjacentes à lista de paredes.
  • Remova a parede da lista.

 neighbors(p::Point) = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right function newalls!(walls, p, maze, n, m) nbrs = neighbors(p) for a in nbrs if 1<ax<n-1 && 1<ay<m-1 && !maze[ax,ay] push!(walls, a) #       . end end end function breakwall!(p, maze, n, m) nbrs = neighbors(p) #       if sum( a-> maze[ax,ay], nbrs) == 1 for a in nbrs if maze[ax,ay] # true =  px == ax ? nx = px : px>ax ? nx = p.x+1 : nx = px-1 py == ay ? ny = py : py>ay ? ny = p.y+1 : ny = py-1 maze[px,py] = true #   maze[nx,ny] = true px = nx py = ny return true end end else return false end end function prim(n, m) M = falses(n,m); #    p = Point(2, 2) M[px,py] = true walls = [] newalls!(walls, p, M, n, m) while length(walls) != 0 p = splice!( walls, rand(1:length(walls)) ) if breakwall!(p, M, n, m) newalls!(walls, p, M, n, m) end end M end 

 primaze = prim(19,19); Gray.(primaze) 

Acontece mais ramificado e não menos impressionante, especialmente o processo de montagem.

E agora implementamos o algoritmo mais comum para encontrar a rota mais curta:

Método A *

• 2 listas de vértices são criadas - pendentes e já revisadas. Um ponto inicial é adicionado aos pendentes; a lista de revisados ​​até o momento está vazia.
• Para cada ponto é calculado $$$H$ - a distância aproximada do ponto ao alvo.
• Na lista de pontos a serem considerados, o ponto com o menor valor $$$H$ . Deixe ela $$$X$ .
• Se $$$X$ - o objetivo, então encontramos a rota.
• Nós carregamos $$$X$ da lista pendente para a lista de já revisados.
• Para cada um dos pontos adjacentes a $$$X$ (denotar esse ponto vizinho $$$Y$ ), faça o seguinte:
  
  • Se $$$Y$ já está na revisão - pule.
  • Se $$$Y$ ainda não está na lista de espera - adicione-o lá.
• Se a lista de pontos a considerar estiver vazia, mas ainda não atingimos a meta, a rota não existe.

Para começar, vamos definir o "ponto" da classe que saberá a que distância está do alvo:

 mutable struct Point_h x::Int64 # horisont y::Int64 # vertical h::Float64 Point_h(x, y) = new(x, y, 0.) end 

Agora, definimos uma operação de comparação para a estrutura, um método para estabelecer a presença de um elemento em uma matriz, bem como a função de remover um elemento, encontrar a distância entre pontos e listar vizinhos:

 import Base: in, == ==(a::Point_h, b::Point_h) = ax==bx && ay==by function in(p::Point_h, Arr::Array{Point_h,1}) for a in Arr if a == p return true end end return false end function splicemin!(Arr)#::Array{Point_h,1} i = argmin( [ah for a in Arr] ) splice!(Arr, i) end dista(u,v) = hypot(vx-ux, vy-uy) # <=> sqrt( (vx-ux)^2 + (vy-uy)^2 ) neighbors(p::Point_h) = [Point_h(px, p.y+1), # up Point_h(px, py-1), # down Point_h(px-1, py), # left Point_h(p.x+1, py)] # right 

Como sempre, operadores obscuros podem ser esclarecidos usando o comando ? por exemplo ?splice ?argmin .

E, na verdade, o próprio método A *

 function astar(M, start, final) #   -       isgood(p) = 1<px<n && 1<py<m && M[px,py] != 0 n, m = size(M) #       start.h = dista(start,final) closed = [] opened = [] push!(opened, start) while length(opened) != 0 X = splicemin!(opened) if X in closed continue end if X == final break end push!(closed, X) nbrs = neighbors(X) ygrex = filter(isgood, nbrs) for Y in ygrex if Y in closed continue else Yh = dista(Y, final) push!(opened, Y) end end end #    closed # return end 

Carregamos a imagem com o labirinto e a apresentamos na forma de uma matriz:

 img0 = load("D:/dat/maze0.png") mazematrix = Float64.(channelview(img0)) 

E nós construímos uma rota para sair de um ponto arbitrário:

 s = Point_h(11,9) # start f = Point_h(4,6) # finish M = copy(mazematrix) route = astar(M, s, f) i = 1 for c in route #   M[cx,cy] = 0.7 #save("D:/dat/Astar$i.png", M) i+=1 end Gray.(M) 

Uma pesquisa de todas as posições é assim:

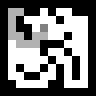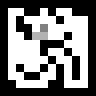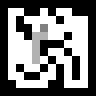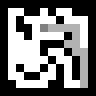
Visto que o agente correndo sempre tende para o lado da saída e geralmente se transforma em becos sem saída, o que dá origem a etapas desnecessárias, e todo o percurso é lembrado. Isso é evitado por uma versão um pouco mais complexa do algoritmo A *.

• 2 listas de vértices são criadas - pendentes e já revisadas. Um ponto inicial é adicionado aos pendentes; a lista de revisados ​​até o momento está vazia.
• Para cada ponto é calculado $$$F = G + H$ . $$$G$ - distância do início ao ponto, $$$H$ - a distância aproximada do ponto ao alvo. Cada ponto também armazena um link para o ponto de onde veio.
• Na lista de pontos a serem considerados, o ponto com o menor valor $$$F$ . Deixe ela $$$X$ .
• Se $$$X$ - o objetivo, então encontramos a rota.
• Nós carregamos $$$X$ da lista pendente para a lista de já revisados.
• Para cada um dos pontos adjacentes a $$$X$ (denotar esse ponto vizinho $$$Y$ ), faça o seguinte:
  
  • Se $$$Y$ já está na revisão - pule.
  • Se $$$Y$ ainda não está na lista de espera - adicione-o, lembrando o link para $$$X$ e tendo calculado $$$Y.G$ (isto é $$$X.G$ + distância de $$$X$ antes $$$Y$ ) e $$$Y.H$ .
  • Se $$$Y$ na lista para consideração - verifique se $$$X.G$ + distância de $$$X$ antes $$$Y$$$$<Y.G$ então chegamos ao ponto $$$Y$ maneira mais curta, substitua $$$Y.G$ em $$$X.G$ + distância de $$$X$ antes $$$Y$ e o ponto de onde eles vieram $$$Y$ em $$$X$ .
• Se a lista de pontos a considerar estiver vazia, mas ainda não atingimos a meta, a rota não existe.

Porém, mesmo com etapas desnecessárias, nossa opção está dentro dos limites da tarefa; portanto, modificar os programas será sua tarefa.

Até o final da Olimpíada, não havia mais nada, mas ainda precisamos aprender a traduzir os resultados de nossos algoritmos em comandos do formato "RRLUUDL..."

E depois de todas essas caminhadas pelos labirintos, podemos assumir que a solução é muito mais simples. De fato, uma opção simples implora imediatamente, mas eu realmente queria fazer coisas bonitas .

Se colocarmos nosso artista em uma área aberta e iniciarmos passeios aleatórios, ele hesitará perto de sua posição inicial. Mas com a introdução das paredes, parte das direções começará a desaparecer, os graus de liberdade se tornarão menores e, com os mesmos dados de entrada, o agente se moverá uma distância maior.

Aqui está a nossa versão de verificar as equipes quanto à adequação para resgatar um robô de um labirinto:

 M = [ 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0] mutable struct Point # point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end function isexit(str, c) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end function test(Str) k = 0 n, m = 10,10 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end 

Agora é suficiente gerar linhas aleatórias até você obter uma que funcione para todas as posições iniciais:

 using Random S = randstring("RLUD",200) "RDRRRDLRLUULURUDUUDLLLLLULLUDRRURDLDLULLRLUUUDURUUUULRUDUURUUDLRLLULRLUDRRLRRULLDULRRRRULRLLDULRLDRUDURDRUUDUUDDDDDLURRRRDRDURRRDDLLDUURRRLDRUDLRLLRDDRLRRRDDLLLRUURDRLURDLLUULLLLUURLLULUDULDDLDLLRLDUD" test(S) 41 test completed from 70 

Além disso, foi possível não se preocupar com o teste. Foi o suficiente para ler a tarefa e gerar uma sequência aleatória com a condição máxima permitida:

 for i in 1:20 S = randstring("RLUD",1000) test(S) end 70 test completed from 70 70 test completed from 70 70 test completed from 70 70 test completed from 70 55 test completed from 70# 65 test completed from 70# 70 test completed from 70 70 test completed from 70 38 test completed from 70# 70 test completed from 70 70 test completed from 70 56 test completed from 70# 70 test completed from 70 70 test completed from 70 70 test completed from 70 16 test completed from 70# 70 test completed from 70 24 test completed from 70# 70 test completed from 70 70 test completed from 70 

Ou seja, com uma probabilidade de 70%, a linha passaria nos testes.

Isso é tudo. Desejo ao leitor uma aleatoriedade, paciência e intuição bem-sucedidas para soluções óbvias.

Para os curiosos - links para aprofundar o tópico:

• A excursão mais completa à geração do labirinto
• Versão russa
• Métodos Times
• Dois métodos
• Algoritmo de Eller
• Gerador online
• Métodos para encontrar o caminho entre pontos online
• Algoritmo do caminho de pesquisa do ponto de salto
• A * na Wikipedia
• Introdução ao A *
• Introdução ao Algoritmo A *
• Explicação do algoritmo de caminho
• Fonte da arte