Este comentário foi motivado pela redação do artigo. Mais precisamente, uma frase disso.

... gastar memória ou processador processando itens em bilhões de dólares não é bom ...

Aconteceu que recentemente eu tive que fazer exatamente isso. E, embora, o caso que considerarei no artigo seja bastante especial - as conclusões e soluções aplicadas podem ser úteis para alguém.

Um pouco de contexto

O aplicativo iFunny lida com uma enorme quantidade de conteúdo gráfico e de vídeo, e a busca difusa de duplicatas é uma das tarefas muito importantes. Esse, por si só, é um grande tópico que merece um artigo separado, mas hoje vou falar um pouco sobre algumas abordagens para calcular matrizes muito grandes de números em relação a esta pesquisa. É claro que todo mundo tem um entendimento diferente de "matrizes muito grandes", e seria tolice competir com o Hadron Collider, mas ainda assim. :)

Se o algoritmo for muito curto, para cada imagem sua assinatura digital (assinatura) será criada a partir de 968 números inteiros e a comparação será feita pela localização da "distância" entre as duas assinaturas. Considerando que o volume de conteúdo nos últimos dois meses chegou a cerca de 10 milhões de imagens, um leitor atento descobrirá isso com facilidade - esses são exatamente os "elementos em bilhões de volumes". Quem se importa - bem-vindo ao gato.

No início, haverá uma história chata sobre como economizar tempo e memória e, no final, haverá uma breve história instrutiva sobre o fato de que às vezes é muito útil olhar para a fonte. Uma imagem para atrair atenção está diretamente relacionada a essa história instrutiva.

Devo admitir que fui um pouco esperto. Em uma análise preliminar do algoritmo, foi possível reduzir o número de valores em cada assinatura de 968 para 420. Já é duas vezes melhor, mas a ordem de magnitude permanece a mesma.

Embora, se você pensar bem, não me engane tanto, e esta será a primeira conclusão: antes de prosseguir com a tarefa, vale a pena pensar - é possível simplificá-la de alguma forma com antecedência?

O algoritmo de comparação é bastante simples: a raiz da soma dos quadrados das diferenças das duas assinaturas é calculada, dividida pela soma dos valores calculados anteriormente (ou seja, em cada iteração a soma ainda será e não pode ser considerada uma constante) e comparada com o valor limite. Vale ressaltar que os elementos de assinatura são limitados a valores de -2 a +2 e, portanto, o valor absoluto da diferença é limitado a valores de 0 a 4.


Nada complicado, mas a quantidade decide.

Primeira abordagem, ingênua

//  const val d = 0.3 // 10.000.000 . //      , //        val collection: MutableList<Signature> = mutableListOf() // signature —   420   Byte class Signature(val signature: Array<Byte>, val norma: Double) fun getSimilar(signature: Signature) = collection .filter { calculateDistance(it, signature) < d } fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> Math.pow((value - second.signature[index]).toDouble(), 2.0) }.sum()) / (first.norma + second.norma) 

Vamos calcular o que temos aqui com o número de operações:

10M Square Roots Math.sqrt
Adições e divisões de 10M / (first.norma + second.norma)
4.200M e quadrado Math.pow((value - second.signature[index]).toDouble(), 2.0)
4.200M adições .sum()

Que opções temos:

1. Com esses volumes, gastar um Byte inteiro (ou, se Deus não permitir, alguém teria adivinhado o uso do Int ) para armazenar três bits significativos é um desperdício imperdoável.
2. Talvez, como reduzir a quantidade de matemática?
3. Mas é possível fazer alguma filtragem preliminar, que não é tão computacionalmente cara?

A segunda abordagem, nós embalamos

A propósito, se alguém sugerir como você pode simplificar os cálculos com essa embalagem, você receberá um grande obrigado e mais em karma. Embora um, mas com todo o meu coração :)

Um Long é de 64 bits, o que, no nosso caso, permitirá armazenar 21 valores nele (e 1 bit permanecerá instável).

 //   20   Long class Signature(val signature: Array<Long>, val norma: Double) fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> calculatePartial(value, second.signature[index]) }.sum()) / (first.norma + second.norma) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L (0..60 step 3).onEach { val current = (first.ushr(it) and 0x7) - (second.ushr(it) and 0x7) sum += current * current } return sum.toDouble() } 

É melhor com a memória ( 4.200M contra 1.600M bytes, se mais ou menos), mas e os cálculos?

Acho óbvio que o número de operações permaneceu o mesmo e 8.400M adicionados 8.400M 8.400M turnos e 8.400M possa ser otimizado, mas a tendência ainda não está feliz - não é isso que queríamos.

A terceira abordagem, reembalar com sub-subs

De manhã eu sinto o cheiro, aqui você pode usar um pouco de mágica!

Vamos armazenar os valores não em três, mas em quatro bits. Desta forma:

Sim, perderemos a densidade de compactação em comparação com a versão anterior, mas teremos a oportunidade de receber Long com 16 (não exatamente) diferenças com um ohm XOR uma só vez. Além disso, haverá apenas 11 opções para a distribuição de bits em cada mordidela final, o que permitirá que você use valores pré-calculados dos quadrados das diferenças.

 //   27   Long class Signature(val signature: Array<Long>, val norma: Double) // -1    val precomputed = arrayOf(0, 1, 1, 4, 1, -1, 4, 9, 1, -1, -1, -1, 4, -1, 9, 16) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L val difference = first xor second (0..60 step 4).onEach { sum += precomputed[(difference.ushr(it) and 0xF).toInt()] } return sum.toDouble() } 

De memória, tornou-se 2.160M versus 1.600M - desagradável, mas ainda melhor do que os 4.200M iniciais.

Vamos calcular as operações:

10M raízes quadradas, adições e divisões (não foram a lugar nenhum)
270M XOR
4.320 adições, turnos, 4.320 lógicos e extrações da matriz.

Já parece mais interessante, mas, de qualquer maneira, há muitos cálculos. Infelizmente, parece que já gastamos esses 20% dos esforços dando 80% do resultado e é hora de pensar em onde mais você pode lucrar. A primeira coisa que vem à mente é não fazer um cálculo, filtrando assinaturas obviamente inadequadas com algum filtro leve.

Quarta abordagem, peneira grande

Se você transformar ligeiramente a fórmula de cálculo, poderá obter essa desigualdade (quanto menor a distância calculada, melhor):


I.e. agora precisamos descobrir como calcular o valor mínimo possível do lado esquerdo da desigualdade com base nas informações que temos sobre o número de bits definido em Long 's. Depois, simplesmente descarte todas as assinaturas que não o satisfazem.
Deixe-me lembrá-lo de que x _i pode assumir valores de 0 a 4 (o sinal não é importante, acho claro o porquê). Dado que cada termo é quadrado, é fácil derivar um padrão geral:


A fórmula final é assim (não precisamos dela, mas deduzi-a por um longo tempo e seria uma pena esquecer e não mostrar a ninguém):


Onde B é o número de bits definido.

De fato, em apenas 64 bits de um Long , leia 64 resultados possíveis. E eles são perfeitamente calculados com antecedência e adicionados a uma matriz, por analogia com a seção anterior.

Além disso, é totalmente opcional calcular todos os 27 Longs - basta exceder o limite no próximo e você pode interromper a verificação e retornar falso. A mesma abordagem, a propósito, pode ser usada no cálculo principal.

 fun getSimilar(signature: Signature) = collection .asSequence() //     !? .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } val estimateValues = arrayOf(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 69, 74, 79, 84, 89, 94, 99, 104, 109, 114, 119, 124, 129, 134, 139, 144, 151, 158, 165, 172, 179, 186, 193, 200, 207, 214, 221, 228, 235, 242, 249, 256) fun estimate(first: Signature, second: Signature):Boolean{ var bitThreshold = Math.pow(d * (first.norma + second.norma), 2.0).toLong() first.signature.forEachIndexed { index, value -> bitThreshold -= estimateValues[java.lang.Long.bitCount(value xor second.signature[index])] if (bitThreshold <= 0) return false } return true } 

Aqui deve ser entendido que a eficácia desse filtro (até negativo) é desastrosamente dependente do limite selecionado e, um pouco menos fortemente, dos dados de entrada. Felizmente, para o limite exigido d=0.3 um número bastante pequeno de objetos consegue passar o filtro e a contribuição de seus cálculos para o tempo total de resposta é tão escassa que pode ser negligenciada. E se sim, você pode economizar um pouco mais.

Quinta abordagem, livrar-se da sequência

Ao trabalhar com coleções grandes, a sequence é uma boa defesa contra a extremamente desagradável falta de memória . No entanto, se obviamente sabemos que no primeiro filtro a coleção será reduzida para um tamanho sensato, uma escolha muito mais razoável seria usar a iteração comum em um loop com a criação de uma coleção intermediária, porque a sequence não é apenas moda e jovem, mas também um iterador, que hasNext companheiros que estão longe de serem gratuitos.

 fun getSimilar(signature: Signature) = collection .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } 

Parece que aqui é felicidade, mas eu queria "torná-la bonita". Aqui chegamos à promissora história instrutiva.

Sexta abordagem, queríamos o melhor

Nós escrevemos no Kotlin, e aqui alguns java.lang.Long.bitCount estrangeiros! E, mais recentemente, tipos não assinados foram trazidos para o idioma. Ataque!

Mal disse o que fez. Todos os ULong substituídos por ULong , ULong extraído da fonte Java e reescrito como uma função de extensão para ULong

 fun ULong.bitCount(): Int { var i = this i = i - (i.shr(1) and 0x5555555555555555uL) i = (i and 0x3333333333333333uL) + (i.shr(2) and 0x3333333333333333uL) i = i + i.shr(4) and 0x0f0f0f0f0f0f0f0fuL i = i + i.shr(8) i = i + i.shr(16) i = i + i.shr(32) return i.toInt() and 0x7f } 

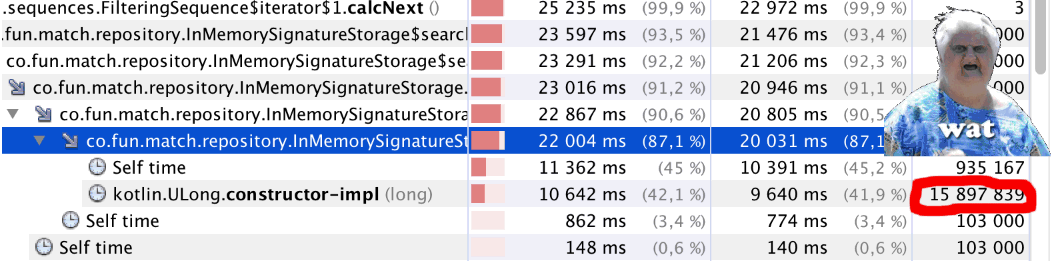
Começamos e ... Algo está errado. O código começou a funcionar visivelmente mais devagar. Iniciamos o criador de perfil e vemos algo estranho (consulte o bitCount() artigo): pouco menos de um milhão de chamadas para bitCount() quase 16 milhões de chamadas para Kotlin.ULong.constructor-impl . WAT!?

O enigma é explicado simplesmente - basta olhar para o código de classe ULong

 public inline class ULong @PublishedApi internal constructor(@PublishedApi internal val data: Long) : Comparable<ULong> { @kotlin.internal.InlineOnly public inline operator fun plus(other: ULong): ULong = ULong(this.data.plus(other.data)) @kotlin.internal.InlineOnly public inline operator fun minus(other: ULong): ULong = ULong(this.data.minus(other.data)) @kotlin.internal.InlineOnly public inline infix fun shl(bitCount: Int): ULong = ULong(data shl bitCount) @kotlin.internal.InlineOnly public inline operator fun inc(): ULong = ULong(data.inc())  .. } 

Não, eu entendo tudo, o ULong é experimental agora, mas como é isso!?
Em geral, reconhecemos a abordagem como falhada, o que é uma pena.

Bem, mas ainda assim, talvez algo mais possa ser melhorado?

Na verdade você pode. O código java.lang.Long.bitCount original não é o mais ideal. Dá um bom resultado no caso geral, mas se soubermos com antecedência quais processadores nosso aplicativo funcionará, podemos escolher uma maneira mais ideal - aqui está um artigo muito bom sobre o Habré. Recomendo a contagem de bits únicos .

Eu usei o "método combinado"

 fun Long.bitCount(): Int { var n = this n -= (n.shr(1)) and 0x5555555555555555L n = ((n.shr(2)) and 0x3333333333333333L) + (n and 0x3333333333333333L) n = ((((n.shr(4)) + n) and 0x0F0F0F0F0F0F0F0FL) * 0x0101010101010101).shr(56) return n.toInt() and 0x7F } 

Contando papagaios

Todas as medições foram feitas a esmo, durante o desenvolvimento na máquina local e são reproduzidas da memória, por isso é difícil falar sobre precisão, mas você pode estimar a contribuição aproximada de cada abordagem.

Conclusões

• Ao lidar com o processamento de grandes quantidades de dados, vale a pena gastar tempo em uma análise preliminar. Talvez nem todos esses dados precisem ser processados.
• Se você pode usar pré-filtragem grosseira, mas barata, isso pode ajudar bastante.
• Um pouco de mágica é o nosso tudo. Bem, onde aplicável, é claro.
• Observar os códigos-fonte das classes e funções padrão às vezes é muito útil.

Obrigado pela atenção! :)

E sim, para continuar.