Pixels de recuo da textura

Apresentamos o quarto artigo de nossa série sobre o trabalho com modelos 3D no Unity. Artigos anteriores: “Recursos de trabalho com o Mesh in Unity” , “Unity: edição procedural do Mesh” , “Importação de modelos 3D para o Unity e armadilhas” .

No artigo anterior, mencionamos a verificação da varredura de textura quanto à adequação da indentação de pixels em uma determinada resolução de textura. Nesta publicação, descrevemos a essência do problema com a observação da indentação de pixels e o algoritmo para rastrea-lo. Não será considerado o código, mas precisamente o princípio que pode ser implementado em qualquer idioma e ambiente de desenvolvimento.

Edição

Um pedido para um modelo 3D geralmente é acompanhado por um requisito para a resolução da textura. Devido à natureza discreta da imagem raster, o artista 3D deve observar o recuo em pixels entre partes da digitalização de textura. A ausência do recuo necessário leva ao fato de que o mesmo pixel é exibido no modelo em locais completamente diferentes quando não é necessário.

É especialmente importante rastrear um recuo suficiente nas fases iniciais do trabalho. Na maioria das vezes, algumas pessoas estão envolvidas na criação da geometria, incluindo uma varredura de textura, e outras estão envolvidas no desenho de texturas. O erro detectado pelo artista 3D causará menos problemas do que o que o designer de texturas encontrará. Neste último caso, a situação se torna ainda mais complicada se o pacote 3D usado não fornecer ferramentas para desenhar sobre geometria (por exemplo, um pincel).

Você também deve considerar duas nuances, pelas quais entre os elementos da varredura pode exigir mais espaço. O primeiro é uma diminuição na resolução da textura durante o mipmapping. O segundo é o uso de um filtro de dilatação ao formar um mapa de iluminação . Durante a tarefa de criar uma digitalização UV , um artista 3D precisa ser guiado pelos requisitos de resolução de textura e também levar em consideração as nuances listadas acima. No entanto, muitas deficiências simplesmente não podem ser percebidas sem a verificação automatizada.


Um exemplo da aparência de artefatos com uma diminuição nos detalhes

Para modelos simples, uma varredura de textura pode ser gerada usando ferramentas automáticas. No entanto, eles são baseados em métricas internas e não levam em conta a indentação de pixels; portanto, os pixels compartilhados geralmente estão localizados ao longo das bordas diagonais. A verificação com texturas de verificador não mostra todos os erros; além disso, essas texturas geralmente têm uma resolução mais alta do que aquelas que serão usadas no projeto.


Pixels compartilhados

O problema da indentação insuficiente de pixels na varredura UV é semelhante ao problema de sobreposições. Nos dois casos, pode ocorrer o chamado sangramento - no artigo anterior , descrevemos quais artefatos isso gera.

No entanto, o problema com a indentação de pixels depende do requisito mínimo de resolução de textura. Uma única verificação é suficiente para determinar as sobreposições, enquanto os requisitos para a resolução da textura podem mudar no próximo estágio de desenvolvimento. A situação é complicada pelo fato de que os pacotes 3D que usamos não possuem ferramentas para detectar automaticamente erros relacionados à proximidade de partes da varredura UV . E não esqueça que, após a operação do modelador automático no Unity, você ainda precisará verificar o UV2 .

Decidimos criar uma ferramenta que pode verificar a indentação em pixels e marcar os locais de possíveis lacunas no modelo. Os requisitos de indentação serão determinados com base nos seguintes parâmetros:

1. A resolução base da textura.
2. A resolução mínima da textura na qual o fluxo não é permitido.
3. O recuo necessário na textura mínima.

Como os tamanhos das texturas que usamos são iguais a dois graus, a fórmula para calcular o recuo necessário na resolução básica é bastante simples: (resolução básica / resolução mínima) * recuo na MinTexture.

Obviamente, a solução para esse problema está intimamente relacionada à rasterização. Para uma declaração mais clara dos requisitos e o desenvolvimento de um algoritmo, apresentamos vários conceitos.

Conceitos chave

Considere um espaço UV e uma grade uniforme da dimensão NxM no intervalo de 0,0 a 1,0. As células com 1 / N de largura e 1 / M de altura formam uma partição do espaço UV .


NxM dividindo o espaço UV

Tomamos dois pontos arbitrários e denotamos Dn como o número de pixels ocupados pela projeção no eixo U do segmento que conecta os pontos dados. Da mesma forma, Dm para o eixo V. Em seguida, definimos a distância do pixel como o máximo entre Dn e Dm.


Distância do pixel

Note-se que no espaço euclidiano, operações de movimento como translação e rotação paralelas não são movimentos para a malha, se a distância do pixel for tomada como métrica. Essa nuance complicou um pouco o desenvolvimento de nossa solução.



Chamamos um quadrado com um lado em K pixels do núcleo de K. Então, quaisquer dois pontos com uma distância de pixel menor que K podem ser cobertos por um núcleo de K.


Exemplos de núcleos de tamanhos diferentes

Duas arestas do polígono formam uma concavidade do contorno se seu ponto médio (o centro de massa em quatro vértices) estiver à esquerda dessas arestas ao contornar o contorno no sentido horário. Para a travessia no sentido anti-horário, a condição é encontrar um ponto à direita das arestas.


Um par de costelas formando uma concavidade do contorno

Solução

Agora vamos falar diretamente sobre a verificação do recuo do pixel. Para implementá-lo, criamos um algoritmo composto por três fragmentos independentes. A ordem de execução não é importante. O resultado de cada um dos fragmentos é a matriz NxM, que é um buffer das células da partição, onde algumas células são rotuladas. A adição de todos os três buffers é o resultado geral.

Primeiro, considere o snippet mais simples. Tudo se resume a encontrar células que se cruzam próximas a triângulos e arestas degeneradas, cujo comprimento é menor que o lado do núcleo de uma dada magnitude. Todas essas células são marcadas no buffer.


Resultado da verificação do tamanho do elemento

Antes de descrever os outros dois fragmentos, considere a lógica geral de seu trabalho. Ambos estão relacionados ao processamento de aglomerados de triângulos chamados de conchas ou ilhas. O shell para um artista 3D é um conjunto conectado de polígonos, ou seja, cada polígono neste conjunto possui um vizinho com o qual compartilha vértices comuns. Também o shell é um campo de treinamento independente. Além disso, por concha, ilha e aglomerado queremos dizer a mesma coisa.



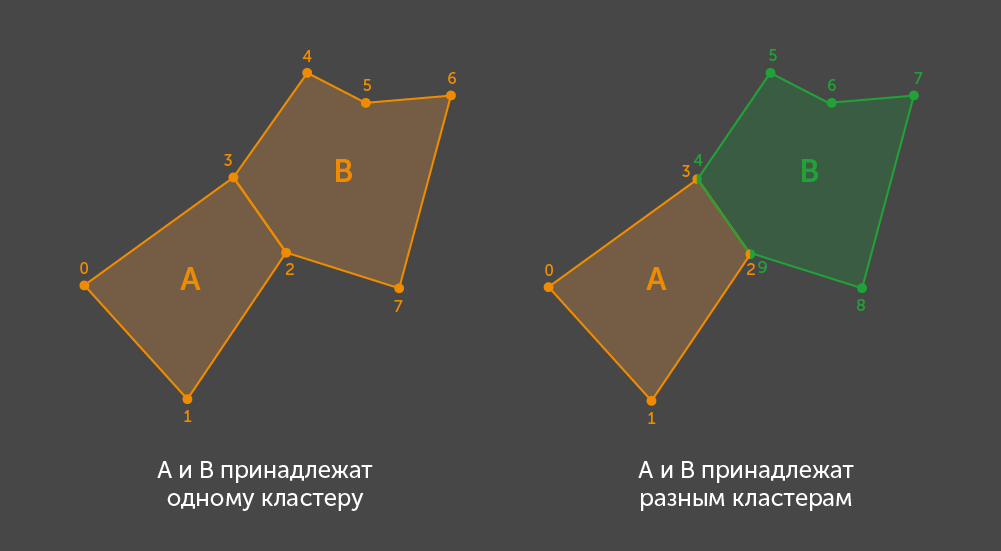
Para encontrar todas as conchas, usamos o algoritmo de busca para todos os componentes conectados do gráfico, em que o vértice do gráfico é representado por um polígono e a aresta pela presença de vértices comuns em um par de polígonos. Como o único polígono no Unity é um triângulo definido por índices de vértices, consideramos triângulos adjacentes se pelo menos um índice do vértice do primeiro coincidir com o índice de qualquer vértice do segundo. Da analogia com o gráfico e o método para determinar arestas, segue-se que o conjunto de índices dos vértices de um cluster não cruza o conjunto de vértices do outro.



Com a parte comum terminada. O segundo fragmento, que consideraremos, determina os locais dos possíveis erros associados à proximidade ou sobreposição de diferentes clusters.

Muitos clusters são alimentados na entrada na forma de conjuntos de triângulos no espaço UV , a dimensão da divisão UV correspondente à resolução da textura (NxM) e o valor de indentação P como o número de pixels. Para uma determinada partição, é necessário encontrar as áreas nas quais a distância em pixels entre os clusters é menor que o recuo necessário. Uma célula na matriz de resultados é marcada se inserir pelo menos um núcleo do valor K = P + 1 , que cruza dois clusters diferentes.

A essência do fragmento está quase definida na descrição do resultado. É necessário encontrar todos os núcleos de magnitude K que se cruzam com triângulos de diferentes conchas e, em seguida, marcar as células desses núcleos no buffer de resultados.

Em nossa implementação, todos os pares de clusters são considerados alternadamente. Para cada par, é determinada a região de interseção dos conjuntos de núcleos de magnitude K cobertos por esses clusters. Escolha um par e denote um conjunto como Q.



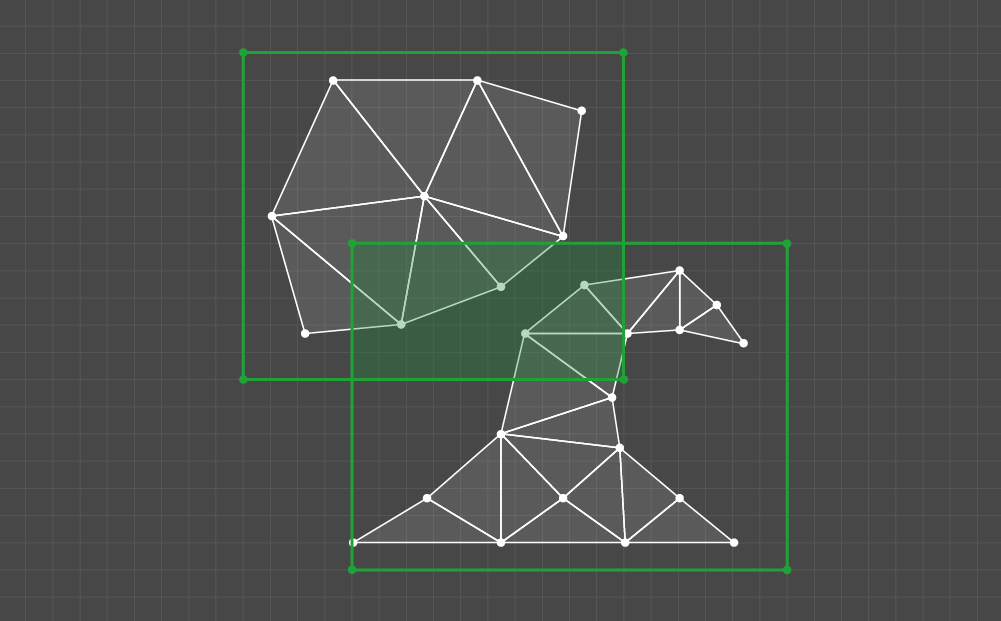
Então, todos os elementos de Q devem ser verificados pelo seguinte critério: o kernel especificado cruza pelo menos um triângulo em cada um dos clusters do par selecionado. Nesse caso, todas as células do kernel testado são marcadas.



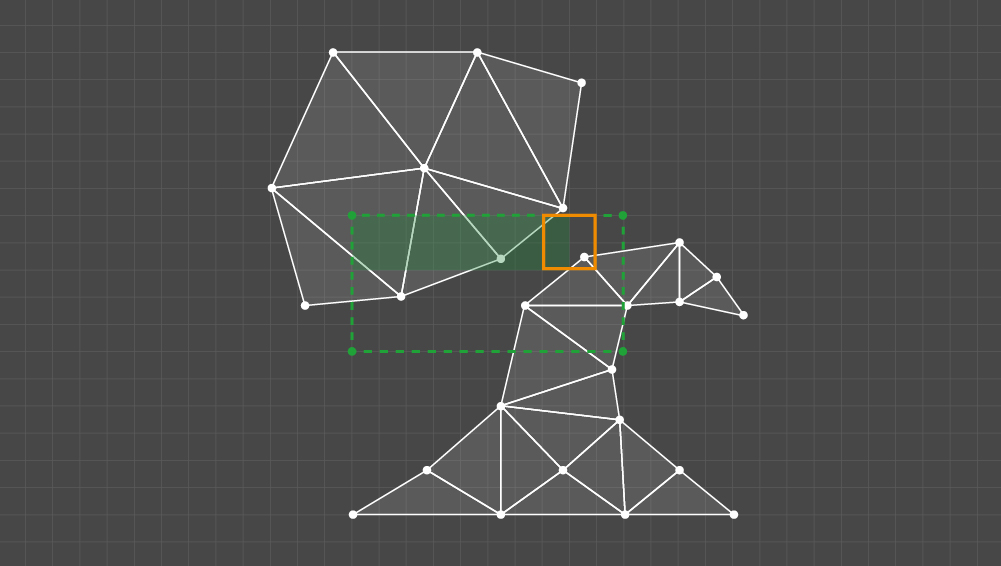
O buffer com células marcadas para todos os pares de clusters constitui o resultado.


Resultado da indentação do cluster

Agora vamos lidar com o último fragmento. Aqui você precisa processar um cluster. A entrada é um conjunto de triângulos no espaço UV , a dimensão da partição UV correspondente à resolução da textura (NxM) e o valor de indentação P como o número de pixels. Uma célula pode ser marcada em dois casos: o cluster é inválido ou possui orifícios ou a distância em pixels entre as bordas da concavidade é menor que o recuo necessário.

A parte interna do cluster não nos interessa - para começar, obteremos seu contorno representado por uma lista conectada de arestas. Triângulos vizinhos duplicam os índices dos vértices; portanto, a aresta pertence ao contorno se um par de índices de seus vértices for exclusivo para o conjunto de arestas do cluster. Depois de descobrir quais bordas formam o contorno, é necessário compor essas bordas para obter uma lista vinculada.

Se após esta etapa nem todas as arestas do contorno entrarem na lista, o cluster terá orifícios ou haverá um erro nos dados da malha. Nesse caso, é necessário marcar adequadamente todas as células dos núcleos interceptadas pelo cluster.

Se o contorno for encontrado, o processamento continuará. Formulamos o seguinte requisito de resultado. Deixe o par de arestas que forma a concavidade do contorno cruzar o núcleo de K = P + 1 . Então as células do núcleo devem ser marcadas se as duas partes do contorno entre as bordas ultrapassarem esse núcleo.


Resultado do teste do recurso de cluster

Decidimos implementar esse requisito através da comparação pareada das arestas do contorno. Começamos com a condição de concavidade e, para cada par, todos os núcleos que cruzam as duas arestas são verificados. Para testar o kernel, são realizadas travessias de cada parte do contorno entre um par de arestas. Se cada parte contiver pelo menos um ponto além dos limites do núcleo, todas as células do núcleo serão marcadas.


A condição sob a qual as células do kernel verificado são marcadas

Sumário

O algoritmo acima é muito adequado para implementação usando computação paralela. O processamento de cada par de clusters e arestas ocorre independentemente. Como as verificações se baseiam na rasterização, se você começar a processar não com pares de arestas, mas com núcleos, é recomendável usar os recursos da GPU .

Transformamos o resultado do algoritmo em uma textura. Para uma determinada resolução, isso permite mostrar graficamente os locais de possíveis falhas na varredura UV . Além disso, a textura resultante pode ser aplicada ao modelo para ver marcas diretamente na geometria.

Nos exemplos abaixo, cortamos especialmente o coelho e Suzanne com a ferramenta automática Blender para obter mais artefatos. A resolução da textura verificada é 256x256, o recuo necessário é 1.

Células marcadas em clusters de capa azul com furos, bem como triângulos e arestas muito pequenas. Verde indica os núcleos celulares com as características de cada cluster individualmente. Os núcleos nos quais o recuo entre os clusters não é observado são marcados em vermelho.


No próximo artigo, consideraremos um algoritmo para otimizar modelos 3D em uma cena, removendo a geometria invisível. Fique conosco!