Para transmitir uma mensagem de uma estação base para um dispositivo móvel (e vice-versa), uma onda eletromagnética precisa superar um número significativo de obstáculos: reflexão, refração, dispersão, sombreamento, mudanças de frequência Doppler e assim por diante. Primeiro, todos esses efeitos são chamados multiplicativos (do inglês. Multiplicação - multiplicação) - de acordo com o modelo matemático de tais efeitos. E, em segundo lugar, pode ser coletada sob o termo geral de desvanecimento .
De padrão em padrão, de geração em geração, de tecnologia em tecnologia, cientistas e engenheiros têm lutado e estão enfrentando o problema de nivelar esses desbotamentos (atenuação de desbotamento).
E algumas soluções são generalizadas. Digamos mais: quase todos, de uma maneira ou de outra, estão associados ao conceito de diversidade .
A fonte da ilustração (não, isso não é publicidade, apenas uma combinação bem-sucedida do termo e do gato desejados).
Um exemplo de tais soluções:
- Salto de frequência - contra desbotamento seletivo de frequência;
- Estimativa e equalização de canais por meio de feedback - GSM, para suprimir mudanças no domínio do tempo;
- Extensão de Espectro (UMTS);
- Sinais piloto (iniciando com UMTS) no downlink (link para baixo) e rastreamento de sinal (rastreamento de sinal) no uplink (link para cima) - para suprimir alterações no domínio do tempo;
- OFDM - LTE, contra desbotamento seletivo de frequência;
- Diversidade temporal ( codificação de correção de erros );
- Diversidade de polarização (no lado do transmissor) + Adicionadores (combinadores, no lado do receptor);
- Diversidade espacial .
A última dessas técnicas que consideraremos hoje como parte de outro tópico no MIMO .
Ordem de diversidade de espaço e ganho de array
O primeiro.
Existe esse conceito - a ordem da diversidade espacial: se a mesma informação puder ser coletada de diferentes direções , a esperança de restaurá-la aumentará corretamente. Como exemplo da vida, podemos imaginar coletar informações sobre o mesmo evento de fontes independentes de informante. Nas comunicações via rádio, podemos aumentar essa ordem, inclusive usando MISO , SIMO ou MIMO .
O limite teórico dessa diversidade 
onde 
- o número de antenas de transmissão, e 
- o número de antenas receptoras. Lembre-se disso.
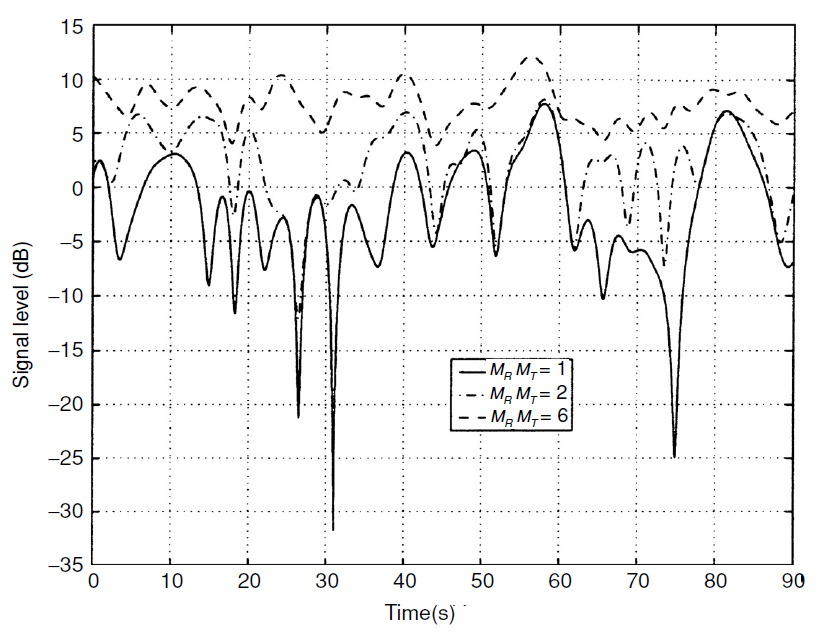
Fig. 1. Estabilidade do canal causada por um aumento na ordem da diversidade espacial. Em valores 
o canal está totalmente estabilizado e se tornará um canal sem desbotamento (AWGN) [1, p . 101] .
O segundo
Usando SIMO , MIMO e até MISO (no caso de um canal conhecido), é possível obter o chamado ganho de matriz . Isso significa que o uso de múltiplas antenas de recebimento e / ou a distribuição correta de energia no lado transmissor pode aumentar a relação sinal-ruído (SNR) - e, assim, reduzir o número de erros.
As ordens de diversidade e ganho de matriz para várias configurações podem ser derivadas analiticamente [1, p. 86 - 100] e reduza para uma tabela [1, p. 101] tanto para o caso em que o canal é desconhecido (CU - Canal desconhecido) quanto para o caso em que o canal é conhecido (CK - Canal desconhecido) na lateral do transmissor.
Ok, mesmo com traços largos, mas agora temos pelo menos alguma compreensão dos aspectos teóricos da supressão do desbotamento. A próxima pergunta é como alcançar esses limites teóricos? Quais são as técnicas para ativar os ganhos considerados?
Solução No. 1. Códigos de tempo espacial
Uma das classes mais populares de soluções para a diversidade espacial é, talvez, a classe de códigos de espaço-tempo (códigos de espaço-tempo). Por exemplo, acho que muitos métodos Alamouti familiares (um exemplo de código de bloco) [2, p. 40-46]:
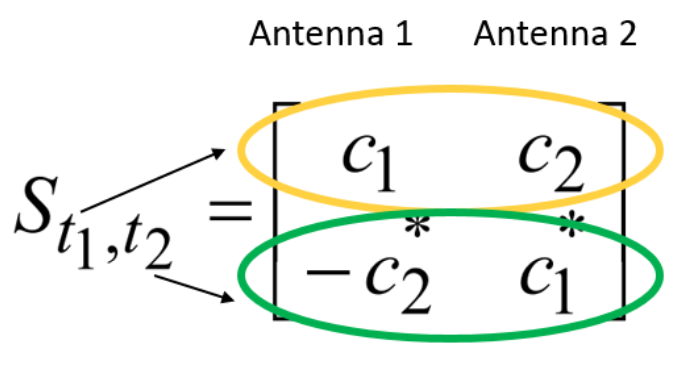
onde 
às 
Alguns caracteres de entrada 
às São os horários e 
- isto é, de fato, uma matriz de codificação.
O esquema Alamouti é ortogonal [1, pp. 93-95, 97-98] e, o mais importante, não requer informações sobre o estado do canal.
A descrição matemática da transmissão do sinal codificado pelo esquema Alamouti, bem como vários exemplos de modelagem dessa técnica no MatLab, podem ser encontrados no meu repositório . Interessado em receber!
No entanto, como você pode ver, o circuito Alamouti é um caso em que temos apenas duas antenas de transmissão ( 
)
Mas não desanime com antecedência: é claro, outras opções estão disponíveis, elas são simplesmente chamadas de forma um pouco diferente. Por exemplo, de acordo com [3], pode-se aplicar os seguintes esquemas de codificação:
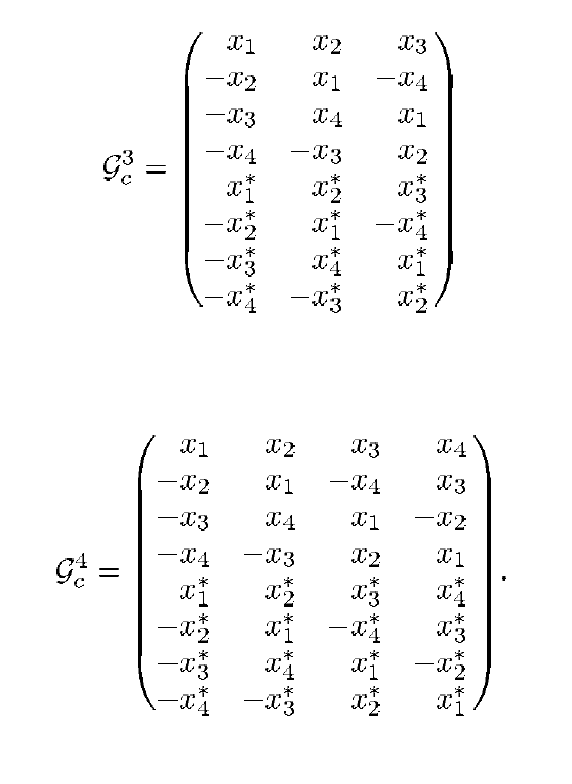
Fig. 2. Regimes de transferência para casos 
e 
[2]
E existem muitas outras opções: apenas para atender às condições da ortogonalidade.
Tais códigos requerem, de fato, os mesmos procedimentos para codificação e decodificação que para o código Alamouti. Portanto, eles são geralmente combinados sob o termo geral de códigos de blocos ortogonais do espaço-tempo (OSTBC - Códigos ortogonais de espaço-tempo ).
É dada muita atenção a essa classe de códigos nos materiais "Introdução aos sistemas MIMO" do MathWorks. Eu recomendo fortemente a todos os interessados em lê-lo!
Qual o preço?
Como pode ser visto no esquema de transmissão, embora transmitamos símbolos em paralelo, gastamos vários intervalos de tempo nisso. Portanto, sacrificamos a largura de banda (pelo menos, obtemos menos). Para o esquema Alamouti, esse compromisso é simétrico: usamos 2 antenas e 2 intervalos de tempo (como se estivéssemos usando o SISO em termos de largura de banda). Outros esquemas podem afetar ainda mais a velocidade de transmissão.
Decisão número 2. DET: Transmissão de modo próprio dominante
Bem, para a classe anterior de técnicas, o conhecimento do canal não era importante para nós. Mas e se ainda tivermos esse conhecimento? Existem técnicas mais adequadas neste caso?
Em um dos meus artigos anteriores, discutimos que, tendo conhecimento do estado do canal em mãos, podemos aplicar vários métodos de processamento de sinal para aumentar a taxa de transferência. O mesmo princípio funciona para aumentar a imunidade ao ruído.
Provavelmente, muitos ouviram falar sobre o método MRC e muitos sabem que esse método é muito adequado para o caso SIMO , quando há pelo menos uma antena na transmissão, mas ainda existem muitas, o que significa que há algo para combinar.
Mas, provavelmente, um número menor de leitores já encontrou o MRC no lado transmissor (Tx-MRC) [1, p. 95.96], e menos ainda com a tecnologia DET (transmissão autônoma dominante) [1, p. 98-100]. Fix it!
Para começar, considere o caso geral do canal MIMO e o último desses métodos - DET.
Qual é a essência de:
- Se o transmissor tiver uma matriz
então pode ser processado. - Por exemplo, decomponha-o via SVD :
obtendo assim várias matrizes de uma determinada propriedade. - Essas propriedades podem ser usadas para otimizar a transferência, por exemplo, usando pré-codificação (pré-codificação).
Introduzimos um vetor de pré-codificação:
onde 
É o primeiro vetor de matriz (dominante, por assim dizer) 
.
Além disso, também podemos escrever o vetor de pós-processamento:
onde 
É o primeiro vetor da matriz 
.
Redefina o modelo do sinal recebido (consulte o tópico largura de banda ):
Voila! A magia da álgebra linear destacou entre todos os caminhos de distribuição os mais rentáveis e direcionou toda a energia para lá. De fato, temos diante de nós um algoritmo de formação de feixe linear.
À custa dessa abordagem, assim como no caso da OSTBC, a limitação da largura de banda é. É verdade que agora isso está acontecendo puramente no domínio espacial.
Por que o método contém valores próprios em seu nome se estávamos falando apenas de valores singulares?Como os valores próprios (cardinalidade dos caminhos de propagação - desbotamento) podem ser diretamente derivados de números singulares (amplitudes de desbotamento):
Bem, com o DET fica mais ou menos claro o que há com o Tx-MRC?
É ainda mais fácil com ele - este é um caso especial do DET, e agora vamos provar isso.
Para Tx-MRC, o seguinte vetor de pré-codificação é proposto na literatura:
Lembramos que o quadrado da norma de Frobenius é igual ao valor próprio e, consequentemente, o quadrado do número singular 
(no caso de SIMO e MISO).
Então, novamente, redefinimos o modelo do sinal recebido, apenas para o caso MISO:
O que era necessário para provar.
Observe que agora estamos falando não apenas da separação de sinais no lado transmissor e combinando-os no lado receptor, como foi o caso da OSTBC. Agora estamos falando sobre a distribuição ideal de energia. Isso significa que os valores de ganho da matriz nesse caso são mais altos que os do OSTBC.
Agora que todas as palavras foram ditas, tentaremos simular nossas técnicas.
Modelagem
Hoje contei um pouco: para a modelagem OSTBC , foram usados objetos prontos da Communication Toolbox (MatLab R2014a - qual era):
Para modulação e desmodulação (e cálculo de erros de bits - BER), as funções não eram mais usadas, mas funções . Seus análogos estão no pacote Octave de comunicações .
Os códigos-fonte podem ser encontrados aqui.clear all; close all; clc snapshots = 100000; EbNo = 0:15; M = 2;
Deveria acontecer algo assim:
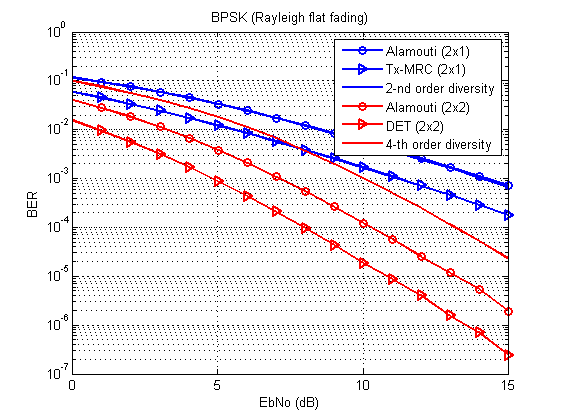
Fig. 3. Curvas de erro de bit / símbolo para diferentes técnicas de transmissão (BPSK, canal Rayleigh com desbotamento plano). Compare com [1, p. 96, 100].
E agora a pergunta é: onde está a curva do limite teórico da diversidade de segunda ordem?
A respostaTudo está de acordo com a tabela: essa curva coincide completamente com o Alamouti 2x1. No caso do MIMO, o ganho de matriz também entra em jogo e, portanto, as curvas são separadas.
De uma forma ou de outra, espera-se que o DET (ou Tx-MRC) supere os Alamouti em qualidade.
Assim: conhecimento é poder!
Literatura
Paulraj, Arogyaswami, Rohit Nabar e Dhananjay Gore. Introdução às comunicações sem fio no espaço-tempo. Cambridge University Press, 2003.
Bakulin M.G., Varukina L.A., Kreindelin V. B. Tecnologia MIMO: princípios e algoritmos // M .: Hot line - Telecom. - 2014 .-- T. 244.
Tarokh, V., Jafarkhani, H., & Calderbank, AR (1999). Códigos de bloco espaço-tempo de desenhos ortogonais. IEEE Transactions on Information theory, 45 (5), 1456-1467.
PS
Aos professores e à fraternidade estudantil da minha profissão nativa , digo olá!