Introdução ao Machine Learning

O curso completo em russo pode ser encontrado neste link .
O curso de inglês original está disponível neste link .



Novas palestras são agendadas a cada 2-3 dias.

Entrevista com Sebastian Trun, CEO da Udacity

"Olá novamente, eu sou Paige e você é meu convidado hoje, Sebastian."
Oi, eu sou Sebastian!
- ... um homem que tem uma carreira incrível, que conseguiu fazer muitas coisas incríveis! Você é co-fundador da Udacity, fundou o Google X, é professor em Stanford. Você vem pesquisando e aprendendo profundamente por toda a sua carreira. O que lhe trouxe mais satisfação e em quais áreas você recebeu mais recompensas pelo trabalho realizado?
- Francamente, eu realmente amo estar no Vale do Silício! Eu gosto de estar perto de pessoas que são muito mais inteligentes do que eu e sempre considerei a tecnologia como uma ferramenta que muda as regras do jogo de várias maneiras - da educação à logística, saúde, etc. Tudo isso muda tão rapidamente, e há um desejo incrível de ser um participante dessas mudanças, de observá-las. Você olha para os arredores e entende que a maior parte do que vê ao seu redor não funciona como deveria - você sempre pode inventar algo novo!
- Bem, essa é uma visão muito otimista da tecnologia! Qual foi o maior eureka ao longo de sua carreira?
- Senhor, havia tantos! Lembro-me de um dia em que Larry Page me ligou e sugeriu a criação de carros de piloto automático que pudessem dirigir por todas as ruas da Califórnia. Naquela época, eu era considerado um especialista, era classificado entre eles e eu era a mesma pessoa que disse "não, isso não pode ser feito". Depois disso, Larry me convenceu de que, em princípio, é possível fazer isso, você só precisa começar e tentar. E nós conseguimos! Foi o momento em que percebi que mesmo os especialistas estão errados e dizendo "não" somos 100% pessimistas. Acho que deveríamos estar mais abertos ao novo.
- Ou, por exemplo, se Larry Page ligar e disser: "Ei, faça algo legal como o Google X" e você terá algo muito legal!
- Sim, com certeza, não precisa reclamar! Quero dizer, tudo isso é um processo que passa por muita discussão no caminho da implementação. Tenho muita sorte de trabalhar e tenho orgulho disso, no Google X e em outros projetos.
- Incrível! Portanto, este curso é sobre como trabalhar com o TensorFlow. Você tem experiência com o TensorFlow ou talvez esteja familiarizado (ouvido) com ele?
Sim! Eu literalmente amo o TensorFlow, é claro! No meu próprio laboratório, nós o usamos com frequência e muito, um dos trabalhos mais significativos baseados no TensorFlow foi lançado há cerca de dois anos. Aprendemos que o iPhone e o Android podem ser mais eficazes na detecção de câncer de pele do que os melhores dermatologistas do mundo. Publicamos nossa pesquisa na Nature e isso criou uma espécie de comoção na medicina.
- Isso parece incrível! Então você conhece e ama o TensorFlow, o que é ótimo em si! Você já trabalhou com o TensorFlow 2.0?
- Não, infelizmente ainda não tive tempo.
- Ele vai ser incrível! Todos os alunos deste curso trabalharão com esta versão.
- Eu os invejo! Definitivamente vou tentar!
Ótimo! Em nosso curso, há muitos estudantes que em sua vida nunca se envolveram em aprendizado de máquina, a partir da palavra "completamente". Para eles, o campo pode ser novo, talvez para alguém que esteja programando seja novo. Que conselho você daria para eles?
- Gostaria que eles permanecessem abertos - a novas idéias, técnicas, soluções, posições. O aprendizado de máquina é realmente mais fácil que a programação. No processo de programação, é necessário levar em consideração cada caso nos dados de origem, adaptar a lógica e as regras do programa. No momento, usando o TensorFlow e o aprendizado de máquina, você basicamente treina o computador usando exemplos, permitindo que o computador encontre as regras.
- Isso é incrivelmente interessante! Mal posso esperar para contar aos alunos deste curso um pouco mais sobre aprendizado de máquina! Sebastian, obrigado por reservar um tempo para vir até nós hoje!
Obrigado! Fique em contato!

O que é aprendizado de máquina?

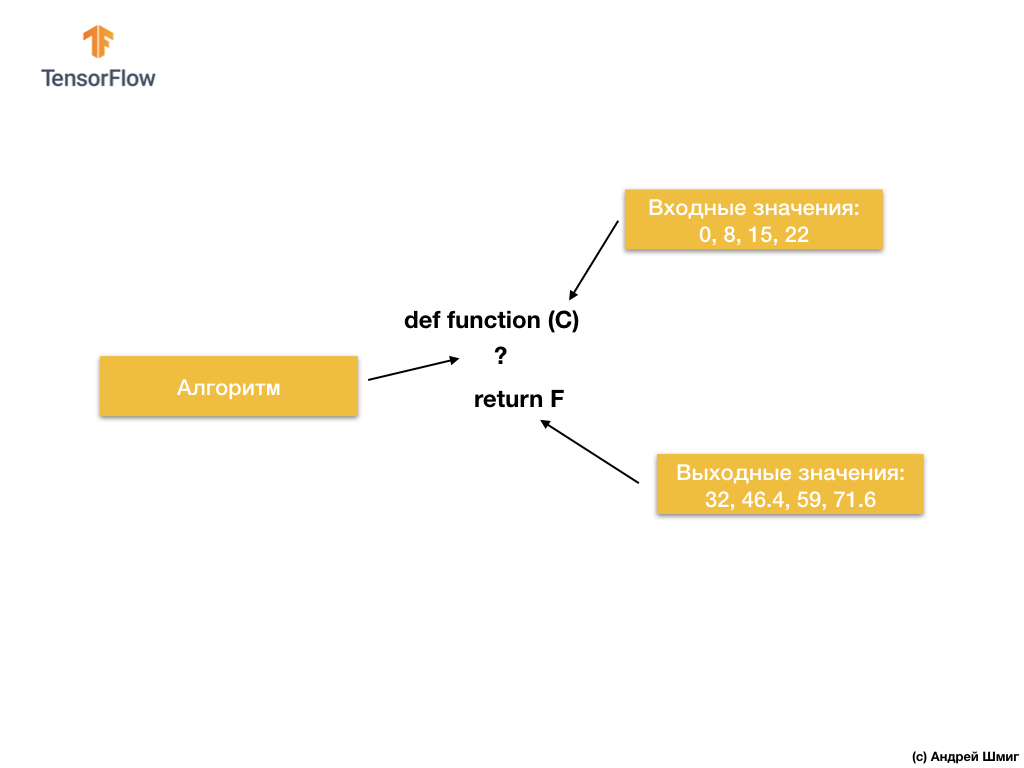
Então, vamos começar com a seguinte tarefa - dados de entrada e saída.



Quando você tiver o valor 0 como valor de entrada, 32 como valor de saída.Quando você tiver 8 como valor de entrada, 46,4 como valor de saída. Quando você tem 15 como valor de entrada, 59 como valor de saída e assim por diante.

Dê uma olhada nesses valores e deixe-me fazer uma pergunta. Você pode determinar qual será a saída se recebermos 38 na entrada?



Se você respondeu 100,4, estava certo!



Então, como poderíamos resolver esse problema? Se você observar atentamente os valores, poderá ver que eles estão relacionados pela expressão:



Onde C - graus Celsius (valores de entrada), F - Fahrenheit (valores de saída).

O que seu cérebro acabou de fazer - comparou valores de entrada e valores de saída e encontrou um modelo comum (conexão, dependência) entre eles - é isso que o aprendizado de máquina faz.

Com base nos valores de entrada e saída, os algoritmos de aprendizado de máquina encontrarão um algoritmo adequado para converter valores de entrada em valores de saída. Isso pode ser representado da seguinte maneira:



Vejamos um exemplo. Imagine que queremos desenvolver um programa que converta graus Celsius em graus Fahrenheit usando a fórmula F = C * 1.8 + 32 .



A solução, ao abordar do ponto de vista do desenvolvimento tradicional de software, pode ser implementada em qualquer linguagem de programação usando a função:



Então o que nós temos? A função pega um valor de entrada C, calcula o valor de saída de F usando um algoritmo explícito e, em seguida, retorna o valor calculado.



Por outro lado, na abordagem de aprendizado de máquina, temos apenas valores de entrada e saída, mas não o próprio algoritmo:



A abordagem de aprendizado de máquina baseia-se no uso de redes neurais para encontrar a relação entre os valores de entrada e saída.



Você pode pensar em redes neurais como uma pilha de camadas, cada uma das quais consiste em matemática (fórmulas) e variáveis ​​internas conhecidas anteriormente. O valor de entrada entra na rede neural e passa por uma pilha de camadas de neurônios. Ao passar pelas camadas, o valor de entrada é convertido de acordo com a matemática (fórmulas fornecidas) e os valores das variáveis ​​internas das camadas, produzindo um valor de saída.

Para que a rede neural seja capaz de aprender e determinar a relação correta entre os valores de entrada e saída, precisamos treiná-la - treiná-la.

Nós treinamos a rede neural através de tentativas repetidas de combinar valores de entrada com valores de saída.



No processo de treinamento, o “ajuste” (seleção) dos valores das variáveis ​​internas nas camadas da rede neural ocorre até que a rede aprenda a gerar os valores de saída correspondentes aos valores de entrada correspondentes.

Como veremos mais adiante, para treinar uma rede neural e permitir que ela selecione os valores mais adequados de variáveis ​​internas, milhares ou dezenas de milhares de iterações (treinamentos) são executadas.



Como uma versão simplificada do entendimento do aprendizado de máquina, você pode imaginar algoritmos de aprendizado de máquina como funções que selecionam os valores de variáveis ​​internas, para que os valores de entrada corretos correspondam aos valores de saída corretos.

Existem muitos tipos de arquiteturas de redes neurais. No entanto, independentemente da arquitetura escolhida, a matemática interna (quais cálculos são executados e em que ordem) permanecerá inalterada durante o treinamento. Em vez de mudar a matemática, as variáveis ​​internas (pesos e compensações) mudam durante o treinamento.

Por exemplo, na tarefa de converter de graus Celsius em Fahrenheit, o modelo começa multiplicando o valor de entrada por um determinado número (peso) e adicionando outro valor (deslocamento). O treinamento do modelo consiste em encontrar valores adequados para essas variáveis, sem alterar as operações realizadas de multiplicação e adição.

Mas uma coisa legal para se pensar! Se você resolveu o problema de converter graus Celsius em Fahrenheit, indicado no vídeo e no texto abaixo, provavelmente o resolveu porque tinha alguma experiência ou conhecimento anterior sobre como realizar esse tipo de conversão de graus Celsius em Fahrenheit. Por exemplo, você pode saber apenas que 0 graus Celsius corresponde a 32 graus Fahrenheit. Por outro lado, os sistemas baseados no aprendizado de máquina não têm conhecimento prévio de suporte para resolver o problema. Eles aprendem a resolver esses problemas, não com base no conhecimento anterior e em sua completa ausência.

Chega de conversa - vá para a parte prática da palestra!

CoLab: converta graus Celsius em graus Fahrenheit

A versão russa do código-fonte do CoLab e a versão em inglês do código-fonte do CoLab .

Noções básicas: aprendendo o primeiro modelo

Bem-vindo ao CoLab, onde treinaremos nosso primeiro modelo de aprendizado de máquina!

Procuraremos manter a simplicidade do material apresentado e apresentar apenas os conceitos básicos necessários para o trabalho. Os CoLabs subsequentes conterão técnicas mais avançadas.

A tarefa que resolveremos é a conversão de graus Celsius em graus Fahrenheit. A fórmula de conversão é a seguinte:

$$

$$f = c \ vezes 1,8 + 32$$

Obviamente, seria mais fácil escrever uma função de conversão em Python ou em qualquer outra linguagem de programação que realizasse cálculos diretos, mas, neste caso, não seria aprendizado de máquina :)

Em vez disso, alimentamos na entrada TensorFlow os graus de entrada em graus Celsius que temos (0, 8, 15, 22, 38) e seus graus correspondentes em Fahrenheit (32, 46, 59, 72, 100). Em seguida, treinaremos o modelo de forma que corresponda aproximadamente à fórmula acima.

Dependências de importação

A primeira coisa que importamos é o TensorFlow . Aqui e a seguir chamamos abreviadamente tf . Também configuramos o nível de registro - apenas erros.

Em seguida, importe o NumPy como np . Numpy nos ajuda a apresentar nossos dados como listagens de alto desempenho.

 from __future__ import absolute_import, division, print_function, unicode_literals import tensorflow as tf tf.logging.set_verbosity(tf.logging.ERROR) import numpy as np 

Preparação de dados de treinamento

Como vimos anteriormente, a técnica de aprendizado de máquina com o professor é baseada na busca de um algoritmo para converter dados de entrada em saída. Como a tarefa deste CoLab é criar um modelo que possa produzir o resultado da conversão de graus Celsius em graus Fahrenheit, crie duas listas - celsius_q e fahrenheit_a , que usamos ao treinar nosso modelo.

 celsius_q = np.array([-40, -10, 0, 8, 15, 22, 38], dtype=float) fahrenheit_a = np.array([-40, 14, 32, 46, 59, 72, 100], dtype=float) for i,c in enumerate(celsius_q): print("{}   = {}  ".format(c, fahrenheit_a[i])) 

-40.0 = -40.0
-10.0 = 14.0
0.0 = 32.0
8.0 = 46.0
15.0 = 59.0
22.0 = 72.0
38.0 = 100.0

Alguma terminologia de aprendizado de máquina:

• Propriedade é o valor de entrada do nosso modelo. Nesse caso, o valor unitário é graus Celsius.
• Os rótulos são os valores de saída que nosso modelo prevê. Nesse caso, o valor unitário é graus Fahrenheit.
• Um exemplo é um par de valores de entrada e saída usados ​​para treinamento. Nesse caso, este é um par de valores de celsius_q e fahrenheit_a sob um determinado índice, por exemplo, (22,72).

Crie um modelo

Em seguida, criamos um modelo. Usaremos o modelo mais simplificado - o modelo de uma rede totalmente conectada (rede Dense ). Como a tarefa é bastante trivial, a rede também consistirá em uma única camada com um único neurônio.

Construindo uma rede

tf.keras.layers.Dense a camada l0 ( l ayer e zero) e a criaremos inicializando tf.keras.layers.Dense com os seguintes parâmetros:

• input_shape=[1] - este parâmetro determina a dimensão do parâmetro de entrada - um único valor. Matriz 1 × 1 com um único valor. Como essa é a primeira (e única) camada, a dimensão dos dados de entrada corresponde à dimensão de todo o modelo. O único valor é um valor de ponto flutuante representando graus Celsius.
• units=1 - este parâmetro determina o número de neurônios na camada. O número de neurônios determina quantas variáveis ​​da camada interna serão usadas no treinamento para encontrar uma solução para o problema. Como essa é a última camada, sua dimensão é igual à dimensão do resultado - o valor de saída do modelo - um único número de ponto flutuante representando graus Fahrenheit. (Em uma rede multicamada, o tamanho e a forma da camada input_shape devem corresponder ao tamanho e forma da próxima camada).

 l0 = tf.keras.layers.Dense(units=1, input_shape=[1]) 

Converter camadas em modelo

Uma vez definidas as camadas, elas precisam ser convertidas em um modelo. Sequential modelo Sequential toma como argumentos a lista de camadas na ordem em que devem ser aplicadas - do valor de entrada ao valor de saída.

Nosso modelo possui apenas uma camada - l0 .

 model = tf.keras.Sequential([l0]) 

Nota
Muitas vezes, você encontrará a definição de camadas diretamente na função de modelo, em vez de sua descrição preliminar e uso subseqüente:

 model = tf.keras.Sequential([ tf.keras.layers.Dense(units=1, input_shape=[1]) ]) 

Compilamos um modelo com uma função de perda e otimização

Antes do treinamento, o modelo deve ser compilado (montado). Ao compilar para o treinamento, você precisa:

• função de perda - uma maneira de medir a que distância o valor previsto está do valor de saída desejado (uma diferença mensurável é chamada de "perda").
• função de otimização - uma maneira de ajustar variáveis ​​internas para reduzir perdas.

 model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) 

A função de perda e a função de otimização são usadas durante o treinamento do modelo ( model.fit(...) mencionado abaixo) para executar cálculos iniciais em cada ponto e otimizar os valores.

A ação de calcular as perdas atuais e a melhoria subsequente desses valores no modelo é exatamente o que é o treinamento (uma iteração).

Durante o treinamento, a função de otimização é usada para calcular ajustes nos valores das variáveis ​​internas. O objetivo é ajustar os valores das variáveis ​​internas de tal maneira no modelo (e isso, de fato, é uma função matemática) para que elas reflitam o mais próximo possível a expressão existente para converter graus Celsius em graus Fahrenheit.

O TensorFlow usa análise numérica para executar esses tipos de operações de otimização, e toda essa complexidade está oculta aos nossos olhos, portanto, não entraremos em detalhes neste curso.

O que é útil saber sobre estas opções:

A função de perda (erro padrão) e a função de otimização (Adam) usadas neste exemplo são padrão para modelos tão simples, mas muitos outros estão disponíveis além deles. Nesta fase, não nos importamos com o funcionamento dessas funções.

Você deve prestar atenção à função de otimização e o parâmetro é o coeficiente da learning rate , que em nosso exemplo é 0.1 . Este é o tamanho da etapa usada ao ajustar os valores internos das variáveis. Se o valor for muito pequeno, serão necessárias muitas iterações de treinamento para treinar o modelo. Demais - a precisão cai. Encontrar um bom valor para o coeficiente da taxa de aprendizado requer algumas tentativas e erros, geralmente varia de 0.01 (por padrão) a 0.1 .

Treinamos o modelo

O treinamento do modelo é realizado pelo método de fit .

Durante o treinamento, o modelo recebe graus Celsius na entrada, realiza transformações usando os valores de variáveis ​​internas (chamadas de "pesos") e retorna valores que devem corresponder a graus Fahrenheit. Como os valores iniciais dos pesos são definidos arbitrariamente, os valores resultantes estarão longe dos valores corretos. A diferença entre o resultado desejado e o real é calculada usando a função de perda, e a função de otimização determina como os pesos devem ser ajustados.

Esse ciclo de cálculos, comparações e ajustes é controlado dentro do método de fit . O primeiro argumento é o valor de entrada, o segundo argumento é o valor de saída desejado. O argumento das epochs determina quantas vezes esse ciclo de treinamento deve ser concluído. O argumento verbose controla o nível de log.

 history = model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) print("  ") 

Nos vídeos a seguir, abordaremos os detalhes de como tudo isso funciona e como exatamente as camadas totalmente conectadas (camadas Dense ) "sob o capô".

Exibir estatísticas de treinamento

O método de fit retorna um objeto que contém informações sobre alterações nas perdas a cada iteração subsequente. Podemos usar esse objeto para criar um cronograma de perdas apropriado. Alta perda significa que os graus Fahrenheit previstos pelo modelo estão longe dos valores reais na matriz fahrenheit_a .

Para visualização, usaremos o Matplotlib . Como você pode ver, nosso modelo melhora muito rapidamente desde o início e, em seguida, chega a uma melhoria estável e lenta até que os resultados se tornem "próximos" - perfeitos no final do treinamento.

 import matplotlib.pyplot as plt plt.xlabel('Epoch') plt.ylabel('Loss') plt.plot(history.history['loss']) 

Usamos o modelo para previsões.

Agora, temos um modelo que foi treinado nos valores de entrada celsius_q e nos valores de saída fahrenheit_a para determinar o relacionamento entre eles. Podemos usar o método de previsão para calcular os graus Fahrenheit pelos quais anteriormente não conhecíamos os graus Celsius correspondentes.

Por exemplo, quanto é 100,0 graus Celsius Fahrenheit? Tente adivinhar antes de executar o código abaixo.

 print(model.predict([100.0])) 

Conclusão:

[[211.29639]]


A resposta correta é 100 × 1,8 + 32 = 212, então nosso modelo se saiu muito bem!

Revisão

• Criamos um modelo usando a camada Dense .
• Nós a treinamos com 3.500 exemplos (7 pares de valores, 500 iterações de treinamento)

Nosso modelo ajustou os valores das variáveis ​​internas (pesos) na camada Dense forma a retornar os valores corretos dos graus Fahrenheit a um valor de entrada arbitrário de graus Celsius.

Olhamos para os pesos

Vamos exibir os valores das variáveis ​​internas da camada Dense .

 print("   : {}".format(l0.get_weights())) 

Conclusão:

    : [array([[1.8261501]], dtype=float32), array([28.681389], dtype=float32)] 

O valor da primeira variável é próximo a ~ 1,8 e o segundo a ~ 32. Esses valores (1,8 e 32) são valores diretos na fórmula para converter graus Celsius em graus Fahrenheit.

Isso é realmente muito próximo dos valores reais na fórmula! Consideraremos esse ponto com mais detalhes nos vídeos a seguir, onde mostraremos como a camada Dense funciona, mas por enquanto você só precisa saber que um neurônio com uma única entrada e saída contém matemática simples - y = mx + b (como uma equação direta), que nada mais é do que nossa fórmula para converter graus Celsius em graus Fahrenheit, f = 1.8c + 32 .

Como as representações são iguais, os valores das variáveis ​​internas do modelo devem convergir para os apresentados na fórmula real, o que aconteceu no final.

Com a presença de neurônios adicionais, valores adicionais de entrada e valores de saída, a fórmula se torna um pouco mais complicada, mas a essência permanece a mesma.

Um pouco de experimentação

Por diversão! O que acontece se criarmos mais camadas Dense com mais neurônios, que por sua vez conterão mais variáveis ​​internas?

 l0 = tf.keras.layers.Dense(units=4, input_shape=[1]) l1 = tf.keras.layers.Dense(units=4) l2 = tf.keras.layers.Dense(units=1) model = tf.keras.Sequential([l0, l1, l2]) model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) print("  ") print(model.predict([100.0])) print(" ,  100    {}  ".format(model.predict([100.0]))) print("    l0: {}".format(l0.get_weights())) print("    l1: {}".format(l1.get_weights())) print("    l2: {}".format(l2.get_weights())) 

Conclusão:

    [[211.74748]]  ,  100    [[211.74748]]       l0: [array([[-0.5972079 , -0.05531882, -0.00833384, -0.10636603]], dtype=float32), array([-3.0981746, -1.8776944, 2.4708805, -2.9092448], dtype=float32)]     l1: [array([[ 0.09127654, 1.1659832 , -0.61909443, 0.3422218 ], [-0.7377194 , 0.20082018, -0.47870865, 0.30302727], [-0.1370897 , -0.0667181 , -0.39285263, -1.1399261 ], [-0.1576551 , 1.1161333 , -0.15552482, 0.39256814]], dtype=float32), array([-0.94946504, -2.9903848 , 2.9848468 , -2.9061244 ], dtype=float32)]     l2: [array([[-0.13567649], [-1.4634581 ], [ 0.68370366], [-1.2069695 ]], dtype=float32), array([2.9170544], dtype=float32)] 

Como você deve ter notado, o modelo atual também é capaz de prever muito bem os graus correspondentes de Fahrenheit. No entanto, se observarmos os valores das variáveis ​​internas (pesos) dos neurônios por camadas, não veremos valores semelhantes a 1,8 e 32. A complexidade adicional do modelo oculta a forma "simples" de converter graus Celsius em graus Fahrenheit.

Fique conectado e, na próxima parte, veremos como as camadas densas funcionam "sob o capô".

Breve resumo

Parabéns! Você acabou de treinar seu primeiro modelo. Na prática, vimos como, por valores de entrada e saída, o modelo aprendeu a multiplicar o valor de entrada por 1,8 e adicionar 32 a ele para obter o resultado correto.



Isso foi realmente impressionante, considerando quantas linhas de código precisamos escrever:

 l0 = tf.keras.layers.Dense(units=1, input_shape=[1]) model = tf.keras.Sequential([l0]) model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) history = model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) model.predict([100.0]) 

O exemplo acima é um plano geral para todos os programas de aprendizado de máquina. Você usará construções semelhantes para criar e treinar redes neurais e resolver problemas subseqüentes.

Processo de treinamento

O processo de treinamento (ocorrendo no método model.fit(...)) consiste em uma sequência muito simples de ações, cujo resultado deve ser o valor das variáveis ​​internas, fornecendo os resultados o mais próximo possível do original. O processo de otimização pelo qual tais resultados são alcançados, chamado descida gradiente , utiliza análise numérica para encontrar os valores mais adequados para as variáveis ​​internas do modelo.

Para participar do aprendizado de máquina, você, em princípio, não precisa entender esses detalhes. Mas para aqueles que ainda estão interessados ​​em aprender mais: a descida do gradiente por meio de iterações altera um pouco os valores dos parâmetros, “puxando-os” na direção certa, até que os melhores resultados sejam obtidos. Nesse caso, “melhores resultados” (melhores valores) significam que qualquer alteração subsequente no parâmetro apenas piorará o resultado do modelo. Uma função que mede o quão bom ou ruim é um modelo em cada iteração é chamada de “função de perda”, e o objetivo de cada “puxar” (ajuste de valores internos) é reduzir o valor da função de perda.

O processo de treinamento começa com o bloco "distribuição direta", no qual os parâmetros de entrada vão para a entrada da rede neural, seguem os neurônios ocultos e depois vão para o fim de semana. O modelo então aplica transformações internas nos valores de entrada e variáveis ​​internas para prever a resposta.

Em nosso exemplo, o valor de entrada é a temperatura em graus Celsius e o modelo previu o valor correspondente em graus Fahrenheit.



Assim que o valor é previsto, é calculada a diferença entre o valor previsto e o correto. A diferença é chamada de "perda" e é uma forma de medir o quão bem o modelo funcionou. O valor da perda é calculado pela função de perda, que determinamos por um dos argumentos ao chamar o método model.compile(...).

Após o cálculo do valor da perda, as variáveis ​​internas (pesos e deslocamentos) de todas as camadas da rede neural são ajustadas para minimizar o valor da perda, a fim de aproximar o valor da saída ao valor de referência inicial correto.



Esse processo de otimização é chamado descida de gradiente . Um algoritmo de otimização específico é usado para calcular um novo valor para cada variável interna quando o método é chamado model.compile(...). No exemplo acima, usamos um algoritmo de otimização Adam.

Não é necessário entender os princípios do processo de treinamento para este curso; no entanto, se você tiver curiosidade suficiente, poderá encontrar mais informações no Curso de falha do Google(A tradução e a parte prática de todo o curso estão estabelecidas nos planos de publicação do autor).

Nesse ponto, você já deve estar familiarizado com os seguintes termos:

• Propriedade : valor de entrada do nosso modelo;
• Exemplos : pares de entrada + saída;
• Tags : valores de saída do modelo;
• Camadas : uma coleção de nós unidos em uma rede neural;
• Modelo : representação da sua rede neural;
• Denso e totalmente conectado : cada nó em uma camada é conectado a cada nó da camada anterior.
• Pesos e compensações : modelar variáveis ​​internas;
• Perda : a diferença entre o valor de saída desejado e o valor de saída real do modelo;
• MSE : , , , .
• : , - ;
• : ;
• : «» ;
• : ;
• : ;
• : ;
• Propagação de retorno : calculando os valores das variáveis ​​internas de acordo com um algoritmo de otimização, começando na camada de saída e em direção à camada de entrada através de todas as camadas intermediárias.

Camadas de sentido

Na parte anterior, criamos um modelo que converte graus Celsius em graus Fahrenheit usando uma rede neural simples para encontrar a relação entre graus Celsius e graus Fahrenheit.

Nossa rede consiste em uma única camada totalmente conectada. Mas o que é uma camada totalmente conectada? Para descobrir isso, vamos criar uma rede neural mais complexa com 3 parâmetros de entrada, uma camada oculta com dois neurônios e uma camada de saída com um único neurônio.



Lembre-se de que uma rede neural pode ser imaginada como um conjunto de camadas, cada uma das quais consiste em nós chamados neurônios. Os neurônios de cada nível podem ser conectados aos neurônios de cada camada subseqüente. O tipo de camada em que cada neurônio de uma camada é conectada um ao outro neurônio da camada seguinte é chamado de camada densa (camada Dense) totalmente conectada (totalmente conectada) ou densa (camada ).



Assim, quando usamos camadas totalmente conectadas keras, informamos que os neurônios dessa camada devem estar conectados a todos os neurônios da camada anterior.

Para criar a rede neural acima, as seguintes expressões são suficientes para nós:

 hidden = tf.keras.layers.Dense(units=2, input_shape=[3]) output = tf.keras.layers.Dense(units=1) model = tf.keras.Sequential([hidden, output]) 

Então, descobrimos o que são os neurônios e como eles estão relacionados. Mas como as camadas totalmente conectadas realmente funcionam?

Para entender o que realmente está acontecendo lá e o que eles estão fazendo, precisamos olhar "por baixo do capô" e desmontar a matemática interna dos neurônios.



Imagine que nosso modelo receba três parâmetros - 1, 2, 3e 1, 2 3- os neurônios de nossa rede. Lembra que dissemos que um neurônio tem variáveis ​​internas? Assim, de w * , e b * são o neurónio variáveis mais interna, também conhecido como o peso e deslocamento. São os valores dessas variáveis ​​que são ajustados no processo de aprendizado para obter os resultados mais precisos da comparação dos valores de entrada com a saída.



O que você definitivamente deve ter em mente é que a matemática interna do neurônio permanece inalterada . Em outras palavras, durante o processo de treinamento, apenas pesos e deslocamentos mudam .

Quando você começa a aprender o aprendizado de máquina, pode parecer estranho - o fato de realmente funcionar, mas é assim que o aprendizado de máquina funciona!

Vamos voltar ao nosso exemplo de conversão de graus Celsius em graus Fahrenheit.



Com um único neurônio, temos apenas um peso e um deslocamento. Você sabe o que? É exatamente assim que a fórmula para converter graus Celsius em graus Fahrenheit se parece. Se substituirmos o w11valor 1.8e, em vez de b1- 32, obteremos o modelo final de transformação!

Se retornarmos aos resultados do nosso modelo a partir da parte prática, prestaremos atenção ao fato de que os indicadores de peso e deslocamento foram "calibrados" de maneira a corresponder aproximadamente aos valores da fórmula.

Criamos propositalmente apenas um exemplo tão prático para mostrar claramente a comparação exata entre pesos e compensações. Colocando o aprendizado de máquina em prática, nunca podemos comparar os valores das variáveis ​​com o algoritmo de destino dessa maneira, como no exemplo acima. Como podemos fazer isso? De jeito nenhum, porque nós nem conhecemos o algoritmo de destino!

Resolvendo os problemas do aprendizado de máquina, testamos várias arquiteturas de redes neurais com um número diferente de neurônios - por tentativa e erro, encontramos as arquiteturas e modelos mais precisos e esperamos que eles resolvam a tarefa no processo de aprendizado. Na próxima parte prática, poderemos estudar exemplos específicos dessa abordagem.

Fique em contato, porque agora a diversão começa!

Sumário

Nesta lição, aprendemos abordagens básicas no aprendizado de máquina e aprendemos como as camadas ( Dense-layers) totalmente conectadas funcionam. Você treinou seu primeiro modelo para converter graus Celsius em graus Fahrenheit. Você também aprendeu os termos básicos usados ​​no aprendizado de máquina, como propriedades, exemplos, rótulos. Entre outras coisas, você escreveu as principais linhas de código em Python, que são a espinha dorsal de qualquer algoritmo de aprendizado de máquina. Você viu que em algumas linhas de código você pode criar, treinar e solicitar uma previsão de uma rede neural usando TensorFlowe Keras.

... e call to action padrão - inscreva-se, coloque um plus e compartilhe :)


YouTube: https://youtube.com/channel/ashmig
Telegrama: https://t.me/ashmig
VK: https://vk.com/ashmig