É sabido que a maioria das séries temporais com as quais um pesquisador tem que lidar não é estacionária e sua análise é significativamente mais complicada do que o estudo de processos estacionários. Como o interesse em wavelets parece ter diminuído, é útil discutir alguns outros instrumentos "não estacionários", que são principalmente adequados para estimar frequências instantâneas, bem como para avaliar espectros instantâneos.
Antes de tudo, faz sentido recuperar o "sinal analítico". Abaixo, o "modelo An" refere-se à impedância instantânea e à potência do sinal de teste após a conclusão de sua parte imaginária (alternada na fase por π / 2).
Mas nem sempre é possível mexer com a transformação de Gilbert. Anteriormente, um método de estimativa espectral autoregressiva adequado para trabalhar com sequências curtas já havia sido
mencionado . Aqui, o "modelo AR" será entendido como o estudo de fragmentos curtos (de 5 amostras) sobrepostos do sinal original, a fim de determinar os coeficientes de auto-regressão de segunda ordem, encontrando os "pólos" do modelo a partir deles, etc.

Ambos os métodos descritos aqui são baseados em um princípio - a suposição de que, em uma pequena vizinhança do momento selecionado, o processo em estudo pode ser aproximado por uma sequência "exponencial" - um complexo (An) ou a soma de dois exponenciais conjugados complexos (AR).
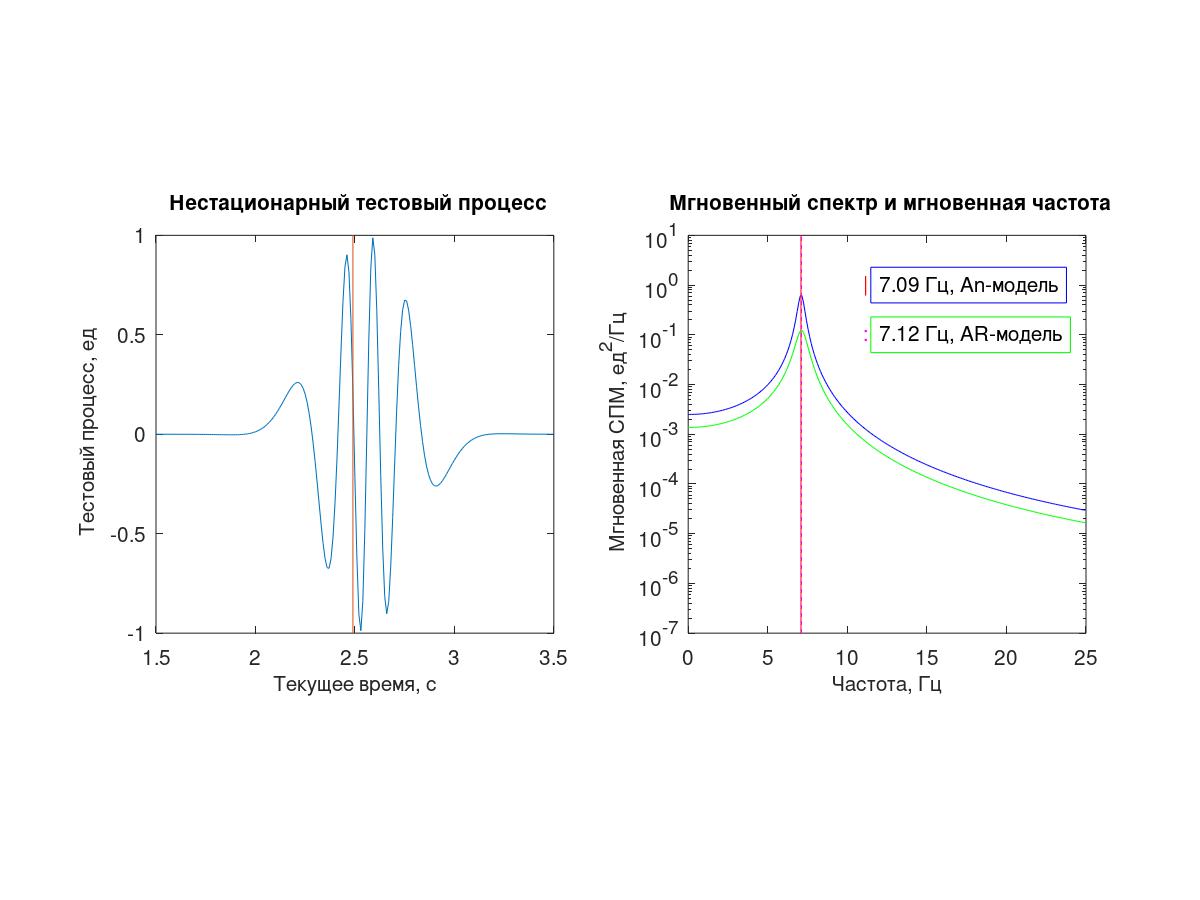
Como processo de teste, foi utilizada uma sequência de 512 amostras com um intervalo de amostragem condicional Δt = 0,01 s obtido de um processo determinístico contínuo (1).
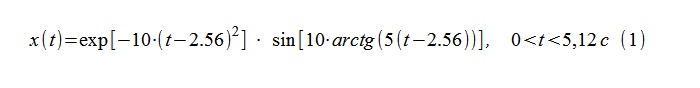
Pelo "logaritmo" e a subsequente diferenciação do enchimento de alta frequência e do envelope, respectivamente, de (1), são obtidas expressões teóricas para a frequência (instantânea) e decremento (2)

Para modelagem An pelo método do periodograma (transformada direta e inversa de Fourier), um sinal analítico y [i] é gerado a partir da sequência inicial x [i].
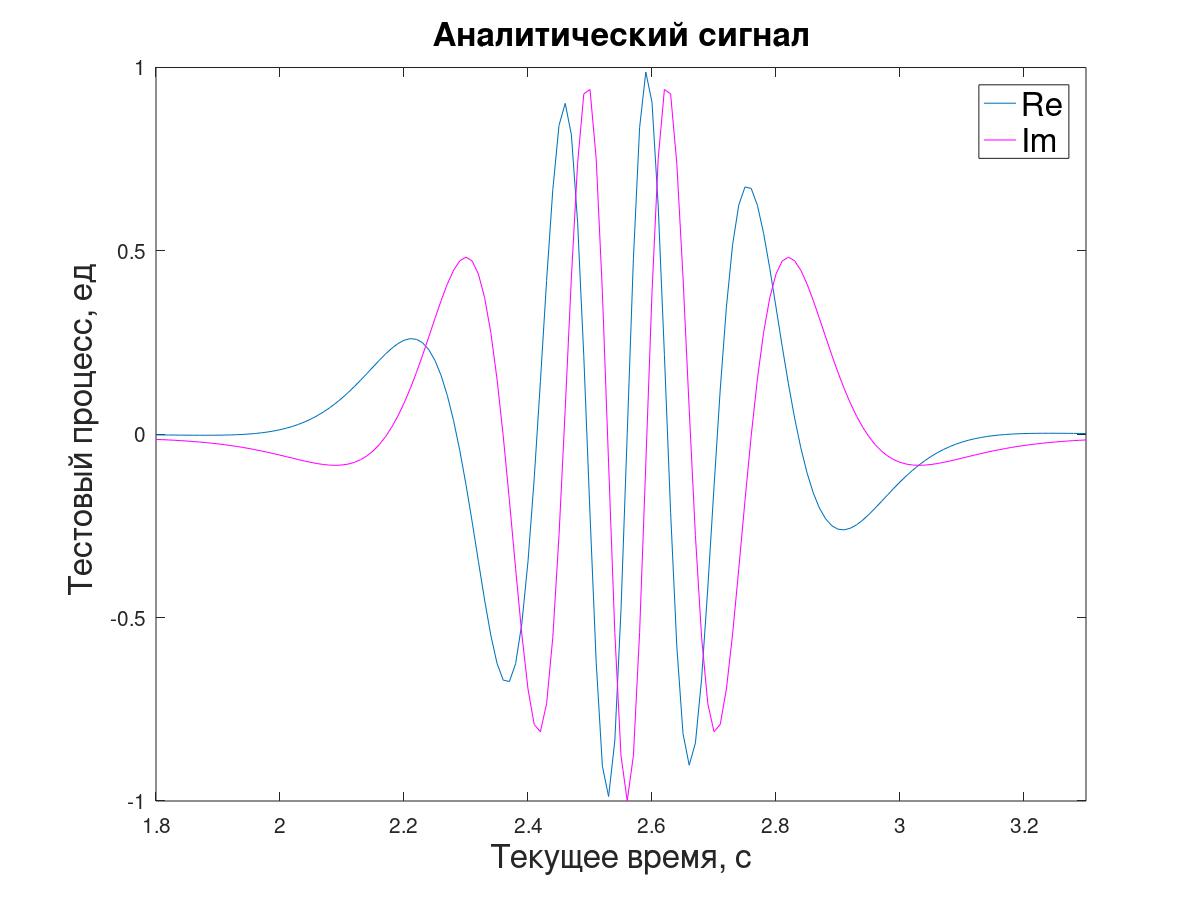
A proporção de duas amostras consecutivas desse sinal, em princípio, permite determinar a impedância instantânea λ, mas para simplificar esta tarefa de demonstração - para não se preocupar em criar amostras intermediárias ou explicar o deslocamento da estimativa por Δt / 2 - foi decidido trabalhar com as amostras “através de um”, calculando λ
i em relação aos valores subsequentes do sinal y [i + 1] em relação ao y anterior [i-1] (3).

Para a modelagem de RA (um modelo de segunda ordem), foi utilizado o procedimento padrão para calcular os coeficientes de autocorrelação 1, a
1i , a
2i usando as equações de Yule-Walker e as sequências de 5 amostras x [i-2], x [i -1], ... x [i + 2] (4).
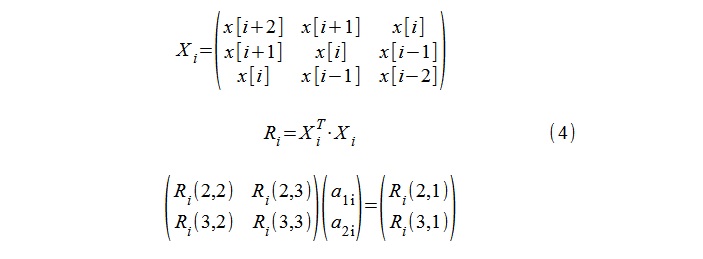
Os “polos” do modelo λ
i são então facilmente calculados pelo logaritmo das raízes da equação quadrática (5).
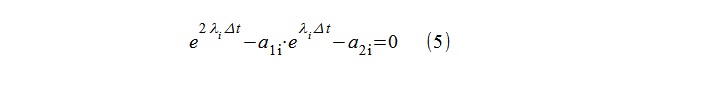

A construção de estimativas espectrais dos polos conhecidos até um fator de escala
não é
difícil . Próximo. O "poder instantâneo" para o modelo An é obviamente definido como | y [i] |
2 , e a questão de escalar essa estimativa parece estar resolvida. Para o modelo de RA, a técnica usual associada à determinação da potência do ruído branco convencional, no caso de um sinal instável, "não funciona". Por falta de melhores idéias, a escala foi aplicada com base no quadrado médio das 5 amostras correspondentes. Parece que nada mais pode ser feito analisando apenas a sequência de 5 amostras. A animação mostra como o gráfico AR do SPM às vezes notavelmente "falha" em relação à pontuação An. Deve-se entender que os momentos da transição “através do zero” para o modelo RA podem ser difíceis não apenas em termos de erros com frequência instantânea, mas também com amplitude instantânea, principalmente na região de baixa frequência.
Alguns comentários no final.
- Por experiência, ambos os métodos geralmente dão bons resultados na estimativa da frequência instantânea, pelo menos na faixa de frequência média (com base na frequência de amostragem).
- A qualidade relativamente alta dos resultados do método An, sua simplicidade e facilidade de entendimento e implementação são mais do que "compensadas" pelas possíveis dificuldades em transformar o processo, segundo Gilbert. Um filtro digital Gilbert de boa qualidade, especialmente em uma ampla faixa de frequência, pode ter uma ordem inaceitavelmente alta. Ao implementar um método alternativo de periodograma dessa transformação, deve-se levar em consideração que a transformação de Fourier implica implicitamente a conclusão do processo em periódico. Como resultado, pode ser necessária uma conclusão significativa e significativa do processo com zeros. A alta qualidade dos resultados do método An é explicada pelo uso de informações em uma vizinhança muito vasta do instante de tempo selecionado (estritamente falando - em toda a implementação temporária do processo), e essa mesma propriedade dificulta a implementação do método (por exemplo, ao trabalhar em tempo real).
- Se necessário, as seguintes medidas podem ser recomendadas para melhorar os resultados do método RA:
- Diluição de dados (a uma taxa de amostragem excessivamente alta)
- Um aumento no número de médias - uma expansão do “momento do tempo” envolvido na vizinhança modelo - a construção de uma matriz de trilhos X com um grande número de linhas.
- Aumentando a ordem do modelo de AR.