Na ciência assíncrona, o lugar central é ocupado pela propriedade dos circuitos, denominados independência da velocidade, em inglês independente da velocidade (a seguir SI). Acredita-se que essa propriedade seja análoga à independência dos circuitos assíncronos dos atrasos dos elementos lógicos. Não é de surpreender que o termo SI seja mencionado em quase todos os trabalhos sobre assincronia. Periodicamente, porém, surgem dúvidas vagas sobre esse termo. Não é por acaso que este termo está sendo cada vez mais substituído por outro termo chamado auto-sincronização. Um apelo à fonte ajudará a esclarecer essa situação. Estamos falando do
segundo volume do livro da Teoria dos circuitos de comutação de R. Miller, ou mais precisamente, do capítulo 10, chamado Teoria dos circuitos de comutação, independente da velocidade.
Então, aqui está a definição de circuitos independentes da velocidade.

Uma classe (equivalência) é um conjunto completo de estados admissíveis de um circuito, de modo que, para qualquer estado desse conjunto, exista uma sequência de estados admissíveis, iniciando em um determinado estado e contendo todos os estados de um determinado conjunto. Em outras palavras, de qualquer estado de uma classe, você pode entrar em qualquer estado da mesma classe.
Uma classe (equivalência) é final se for impossível passar dos estados de uma determinada classe para um estado pertencente a outra classe.
Por exemplo, todos os padrões de vida (comportamentos) são independentes da velocidade. Além disso, eles não dependem da velocidade do circuito, que eventualmente acaba necessariamente, e em um único estado.
Além disso, o autor estabelece uma conexão entre os esquemas de SI, por um lado, e com os esquemas de distribuição semi-modular, seqüencial, por outro. E, em conclusão, ele cita uma lista de propriedades notáveis de circuitos independentes da velocidade.

O primeiro ponto é especialmente interessante. Diz apenas que os circuitos independentes da velocidade não dependem de atrasos nos elementos lógicos. Infelizmente, o texto não indica explicitamente os motivos dessa conclusão. Talvez seja essa a razão dos subsequentes mal-entendidos sobre o termo SI. Na realidade, essa conclusão é completamente verdadeira. No início do capítulo 10, o autor fornece regras para o cálculo de estados subsequentes.

A transição do circuito para o próximo estado é o resultado da alteração da saída de algum elemento lógico (ou das saídas de vários elementos). Ou seja, o intervalo de tempo entre a criação de condições para alternar um elemento lógico (excitação) e sua própria alternância não é limitado por nada. E esse período de tempo é um atraso do elemento lógico. Ou seja, desde o início, o autor parte da suposição de que os atrasos dos elementos lógicos podem ser arbitrariamente grandes. De fato, o seguinte é escrito um pouco mais.

Bem, para dissipar todas as dúvidas, uma citação da primeira página do capítulo 10.

Assim, um fato incontestável foi estabelecido: a independência dos atrasos dos elementos lógicos não é uma propriedade de um circuito, mas uma propriedade do modelo em que esse circuito é investigado. Ou seja, qualquer circuito, SI ou não SI, investigado da mesma maneira como descrito por R. Miller, é independente dos atrasos dos elementos lógicos. Ao mesmo tempo, qualquer circuito pode ser investigado em um modelo com um atraso limitado. Nesse modelo, o conjunto de estados admissíveis é um subconjunto do conjunto de estados admissíveis quando se considera o mesmo esquema em um modelo com atraso ilimitado de elementos. Ao examinar um circuito em um modelo com um atraso de elemento limitado, o circuito pode ser independente da velocidade e, ao mesmo tempo, depender dos atrasos do elemento.
Assim, verifica-se que a independência do circuito dos atrasos dos elementos lógicos não está de forma alguma ligada à propriedade SI. Surge então a questão: qual é o sentido de introduzir uma definição de independência da velocidade? De fato, considere dois padrões e seu comportamento.
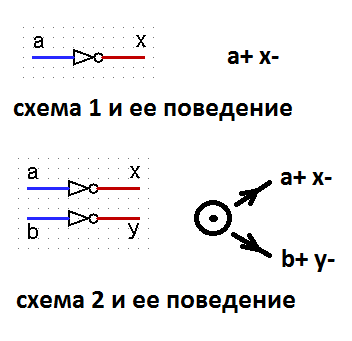
Os sinais a, b para ambos os circuitos são de entrada, os sinais x, y são emitidos. Ambos os esquemas implementam comportamentos perfeitamente razoáveis. Mas, ao mesmo tempo, o circuito 1 não depende da velocidade e o circuito 2 não possui essa propriedade. Sim, podemos dizer que a definição de SI foi introduzida sem dividir os sinais em entrada e saída. Mas essa separação de sinais pelo autor estava implícita, e há uma observação no texto sobre isso.
A significância e razoabilidade da introdução da definição da propriedade SI é revelada apenas em conexão com a propriedade semi-modularidade. Para circuitos com a propriedade de semi-modularidade, cada sinal pode remover sua excitação apenas através de sua comutação. Esquemas não semi-modulares durante a implementação física estão repletos de falhas e estados metaestáveis. Somente esquemas semi-modulares podem ser considerados estáveis.
Mas a conexão entre as propriedades da semi-modularidade e a independência da velocidade é unilateral. Ou seja, esquemas semi-modulares são independentes da velocidade, mas o inverso não é verdadeiro. Os circuitos SI podem não ser semi-modulares. Ou seja, uma propriedade realmente importante que divide os circuitos de acordo com a estabilidade é a semi-modularidade. É importante entender que os circuitos semi-modulares também podem depender de atrasos nos elementos lógicos, se os considerarmos em um modelo com um atraso limitado.
Mas isso não é tudo. A propriedade semi-modularidade também é definida para circuitos autônomos, ou seja, sem dividir os sinais em entrada e saída. Por esse motivo, os esquemas de livre escolha (comportamentos) não atendem aos critérios de semi-modularidade. Enquanto isso, esses esquemas podem ser tão estáveis quanto semi-modulares. Por exemplo, o esquema 2 acima não é semi-modular, mas em termos de estabilidade, não é de forma alguma inferior ao esquema 1, que é semi-modular.
Existe uma saída para esse impasse. O livro J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno, A. Yakovlev “Síntese Lógica para Controladores Assíncronos e Interfaces” define a definição de propriedade de persistência de saída (OP).

É a propriedade OP que é a propriedade real que separa os esquemas (comportamentos) em estáveis e não estáveis. É a propriedade OP que deve substituir a propriedade SI. Não se deve esquecer que a independência dos atrasos dos elementos lógicos é uma propriedade do modelo no qual os circuitos (comportamentos) são estudados. E os circuitos OP também podem depender de atrasos de elemento se considerados em um modelo de atraso limitado.
Apesar de todas as críticas anteriores, não há queixas contra R. Miller. Não há erros lógicos em seu trabalho. A culpa por mais de meio século de erro recai mais sobre os leitores que interpretaram mal o trabalho de R. Miller.
E, finalmente, uma conclusão agradável do exposto. O Modelo Comportamental STG fornece um atraso ilimitado para elementos lógicos. As regras para alterar marcações e extrair a tabela verdade são formuladas a partir da suposição de elementos de atraso ilimitados. Portanto, qualquer circuito obtido pela computação de funções lógicas usando STG (usando uma tabela verdade ou diretamente usando um gráfico) é obviamente independente dos atrasos dos elementos lógicos. É verdade que deve ser entendido que manipulações adicionais com o esquema resultante podem levar à perda dessa valiosa qualidade.