Todas as descrições das mudanças são uma mistura única de acaso e determinismo, de acordo com a prova radical da "hipótese fraca" de Pinsker
Imagine um jardim onde todas as flores do mundo crescem - orquídeas delicadas, girassóis altos, flores de cera do cacto Carnegie e inflorescências fedorentas do
amorphophallus titânico . Agora imagine que toda essa diversidade de plantas se reduza a apenas duas opções e que, ao cruzá-las, você pode produzir todas as outras.
Essa é a natureza de uma das evidências mais radicais obtidas nos últimos anos. Foi feito por
Tim Austin , um matemático da Universidade da Califórnia em Los Angeles. Mas, em vez de flores, o trabalho de Austin está associado a um dos objetos mais estudados em matemática: uma descrição matemática de mudanças.
Essas descrições, conhecidas como
sistemas dinâmicos , aplicam-se a tudo, desde movimentos planetários a flutuações do mercado de ações. Onde quer que um sistema dinâmico surja, os matemáticos querem entender seus fundamentos. E um dos fatos básicos é que qualquer sistema dinâmico arbitrariamente complexo pode ser dividido em elementos aleatórios e determinísticos.
Essa questão é o assunto da "hipótese fraca" de Pinsker, formulada pela primeira vez na década de 1970. A prova da hipótese apresentada por Austin fornece um método elegantemente intuitivo de pensar sobre todos os tipos de fenômenos obscuros. Ele mostrou que, em essência, cada um desses sistemas dinâmicos é uma mistura de acaso e determinismo.
Destino e chance
Um sistema dinâmico começa com alguns dados de entrada, por exemplo, com a posição do pêndulo, aplica certas regras, por exemplo, as leis do movimento de Newton e produz um certo resultado, por exemplo, a posição do pêndulo em um segundo. O que é importante, os sistemas dinâmicos permitem repetir esse processo: você pode assumir uma nova posição do pêndulo, aplicar as mesmas regras e obter sua posição em outro segundo.
Os sistemas dinâmicos também são puramente matemáticos. Você pode selecionar o número inicial, aplicar a regra "multiplique o número por dois" e obter um novo. Esse sistema também permite inserir o número total de volta no manipulador de regras e obter ainda mais números.
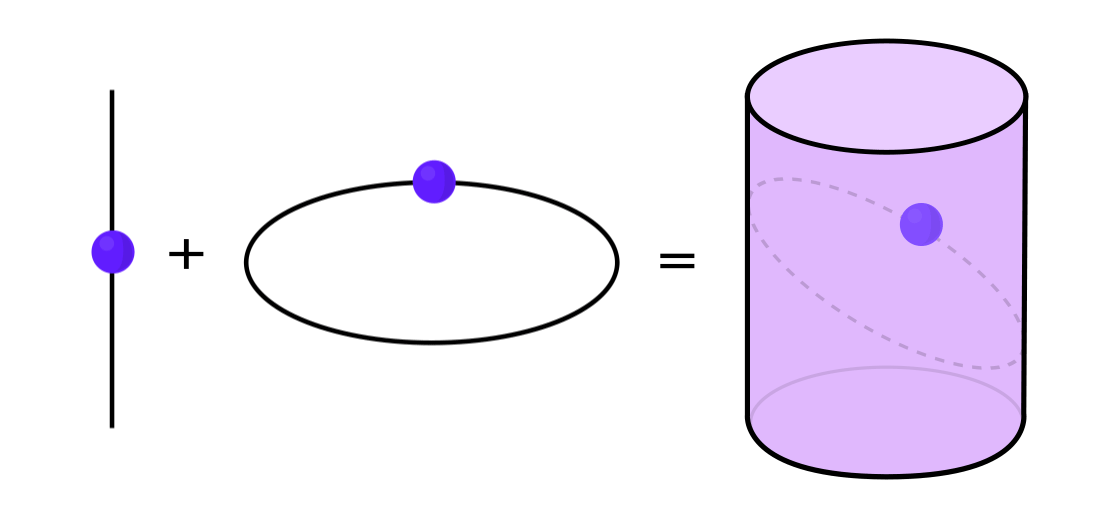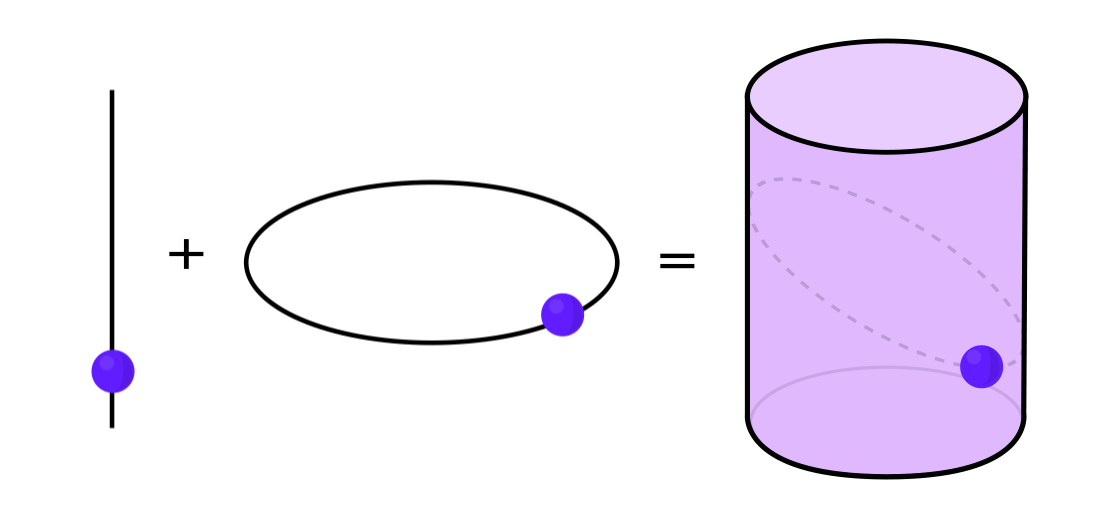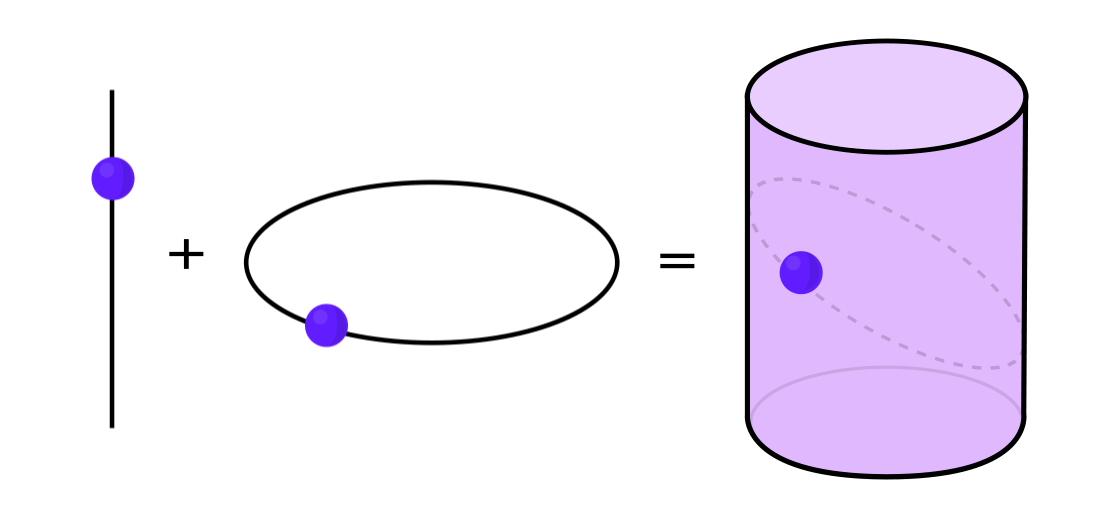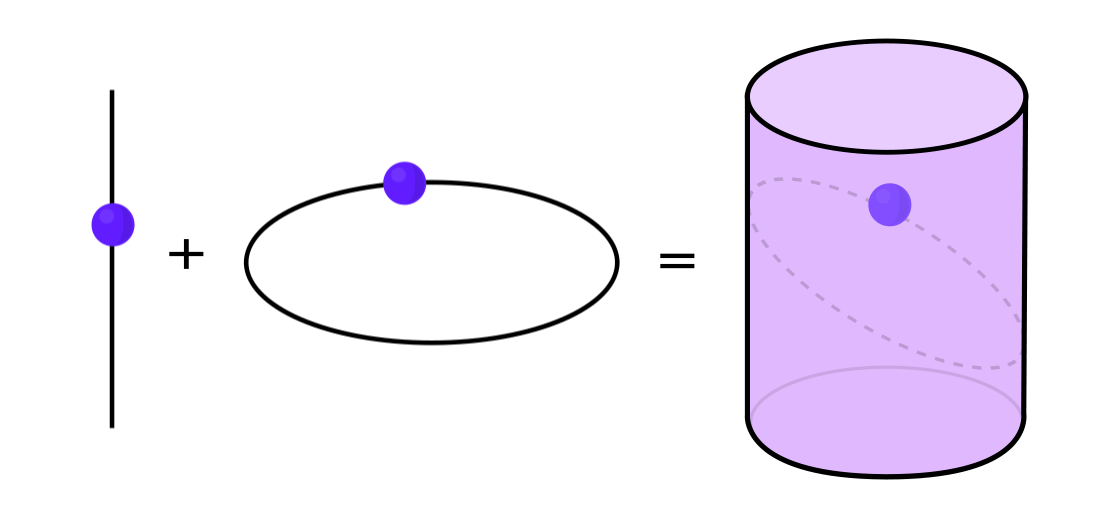
Certos tipos de sistemas dinâmicos podem ser expressos como uma combinação de dois sistemas dinâmicos mais simples. Esses dois sistemas funcionam independentemente um do outro, mas podem ser combinados para formar um mais complexo. Por exemplo, imagine um sistema dinâmico movendo um ponto ao longo da superfície de um cilindro. Você entra na posição do ponto, aplica as regras e obtém outro ponto.
Este sistema pode ser desmontado em dois simples. O primeiro é um sistema dinâmico que move um ponto em torno de um círculo. O segundo é um sistema que move um ponto para cima e para baixo verticalmente. Ao combinar dois sistemas - movimento circular e movimento reto - obtemos um movimento pontual mais complexo ao longo do cilindro.
"Em vez de estudar todo o sistema dinâmico em sua totalidade, é necessário dividi-lo em partes, pequenas partes que fazem sentido estudar", disse
Catherine Lindsay , matemática do Boston College.
Existem dois candidatos naturais para o papel desses blocos de construção. Os primeiros são sistemas dinâmicos totalmente determinísticos, como o nosso exemplo do pêndulo. Se você souber a posição do pêndulo em algum momento, poderá prever a qualquer momento no futuro.
 Jean-Paul Tuveno em 1975, dois anos antes da formulação da hipótese fraca de Pinsker
Jean-Paul Tuveno em 1975, dois anos antes da formulação da hipótese fraca de PinskerO segundo tipo de sistemas dinâmicos é completamente aleatório. Por exemplo, imagine um sistema dinâmico com esta regra: jogue uma moeda. Se houver uma águia, dê um passo para a esquerda; se caudas, certo. O caminho final será completamente aleatório, ou seja, mesmo se você souber tudo sobre o caminho anterior, essas informações não ajudarão a prever o próximo passo.
Alguns sistemas dinâmicos são completamente aleatórios, outros são completamente determinísticos e a maioria está entre os dois - eles são um híbrido de ambos. Por exemplo, imagine uma versão ligeiramente modificada da nossa caminhada aleatória. Caminhamos por um caminho ao longo da borda do qual as flores são plantadas e suas cores também são aleatórias. A regra permanece a mesma: se uma águia cair, vá para a esquerda; se caudas, certo. Qual será a sequência das cores das flores?
Primeiro você diz aleatoriamente. Afinal, as próprias cores foram escolhidas aleatoriamente e seu movimento também é aleatório. No entanto, depois que você passa uma única flor, a probabilidade de que você a passe no futuro aumenta, simplesmente porque você não está longe disso. A sequência das cores das flores não será completamente aleatória.
"Se você ficar ao lado do vermelho, aumenta as chances de que, em duas etapas, você encontre o vermelho novamente, porque pode acontecer que você pise para a esquerda, depois para a direita e volte ao mesmo lugar", disse Austin.
Tal “passeio aleatório por uma paisagem aleatória” produz saída - uma sequência de cores - parcialmente aleatória e parcialmente não. Em 1960, o matemático Mark Pinsker sugeriu que uma certa classe grande de sistemas dinâmicos tem a seguinte propriedade: eles são uma mistura de um sistema dinâmico aleatório com um determinístico.
A conjectura de Pinsker é aplicável à classe de sistemas dinâmicos que possuem uma importante propriedade comum. Os pontos neles não se afastam um do outro e não diminuem durante o desenvolvimento do sistema. Mais precisamente, se você desenhar um loop em torno de um conjunto de pontos em seu espaço (o espaço pode ser algo como uma superfície de cilindro), inicie o desenvolvimento de um sistema dinâmico por um longo período de tempo e, em seguida, faça um loop em torno do conjunto de pontos resultante e, em seguida, a área na qual os pontos apontam final, coincide com a área que eles ocupavam no início. Esses sistemas são chamados de "preservação de medida"
"Se a hipótese original de Pinsker fosse verdadeira, seria uma descrição incrível do mundo", disse
Assaf Naor , matemático da Universidade de Princeton. Mas Pinsker estava errado. Em 1973,
Donald Ornstein refutou sua hipótese. "A redação era muito ambiciosa", disse
Brina Kra , matemática da Northwestern University.
Em matemática, muitas vezes acontece que, depois que a hipótese geral é refutada, os matemáticos tentam formular uma versão mais modesta dela. Em 1977, o matemático Jean-Paul Tuveno propôs a hipótese fraca de Pinsker. Ele amoleceu a formulação original, sugerindo que os sistemas dinâmicos que Pinsker tinha em mente eram o resultado da combinação de um sistema puramente aleatório com um sistema quase completamente determinístico.
O refinamento "quase" distingue a hipótese de Tuveno da hipótese de Pinsker. Ele quis dizer que um sistema determinístico simples deveria ter algum traço de chance. Esse rastreamento pode estar desaparecendo pequeno, mas deve estar lá. E enquanto ele estiver, disse Tuveno, a ideia de Pinsker funcionará.
"Era próximo da hipótese original, e Tuveno mostrou que, nesse caso, a hipótese terá um grande número de excelentes aplicações", disse Naor.
Nas décadas seguintes, os matemáticos não obtiveram muito sucesso em provar a fraca hipótese de Pinsker. A falta de progresso fez Tuveno pensar que até mesmo suas palavras enfraquecidas acabariam erradas. "A certa altura, pensei que tudo seria o contrário, que não seria universal", disse ele.
E então Tim Austin apareceu.
Solução passo
Para provar a fraca hipótese de Pinsker, era necessário encontrar uma maneira exata de filtrar um sistema dinâmico - um que permitisse separar suas partes aleatórias e quase determinísticas. Trabalhos anteriores estabeleceram que será mais difícil isolar elementos com um pouco de aleatoriedade.
"Pequenos fatores aleatórios são muito mais difíceis de entender, e a parte central das evidências é encontrar uma maneira de detectar uma pequena estrutura aleatória", disse Tuveno.
 Tim Austin, matemático da Universidade da Califórnia, Los Angeles
Tim Austin, matemático da Universidade da Califórnia, Los AngelesAustin conseguiu lidar com pequenos elementos aleatórios de um sistema dinâmico, mudando as perspectivas. Os sistemas dinâmicos operam em um espaço contínuo, como um ponto que se move ao longo da superfície de um cilindro ou um pêndulo balançando no espaço. Nesses espaços, os pontos se movem ao longo de arcos contínuos de acordo com as regras de um sistema dinâmico. Além disso, esses sistemas funcionam em um número infinito de etapas - eles podem agir para sempre.
Mas, como prova, Austin abandonou o espaço suave e contínuo e esqueceu o trabalho eterno dos sistemas dinâmicos. Em vez disso, ele começou a analisar o que aconteceria se eles pudessem trabalhar em horários discretos, como um milhão de etapas. Assim, ele aplicou o método inventado por Tuveno.
"A principal contribuição de Tuveno foi que ele percebeu que se você executar as etapas matemáticas corretas com longas linhas finitas, poderá provar as propriedades de um sistema dinâmico", disse Austin. "Minha principal contribuição foi que eu provei o que era necessário para as longas filas."
Austin imaginou um sistema dinâmico emitindo uma sequência de uns e zeros. Se o sistema dinâmico estiver jogando uma moeda, é fácil imaginar: as caudas serão 1 e as cabeças serão 0. Mas qualquer sistema dinâmico pode ser usado para gerar uma sequência binária simplesmente dividindo o espaço em que funciona em duas (não necessariamente iguais) peças.
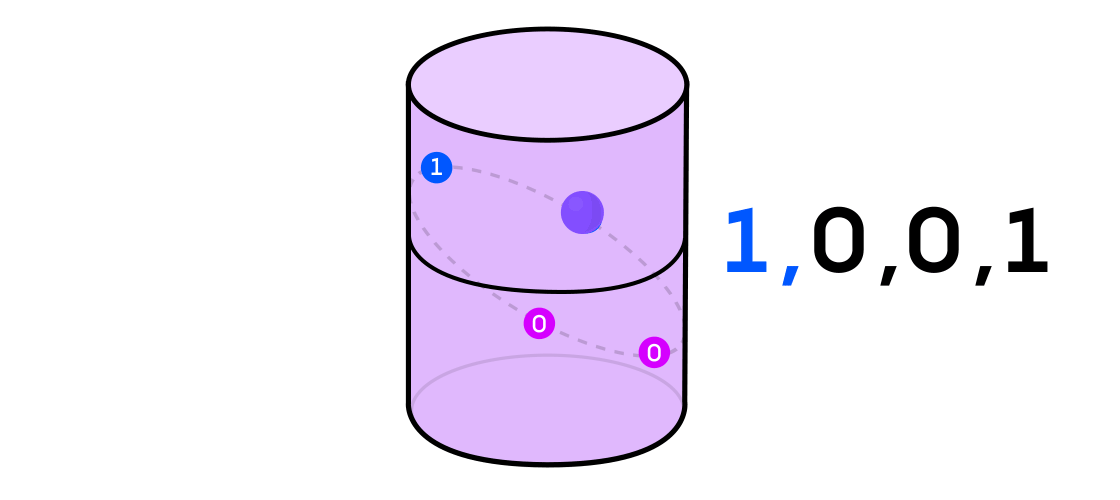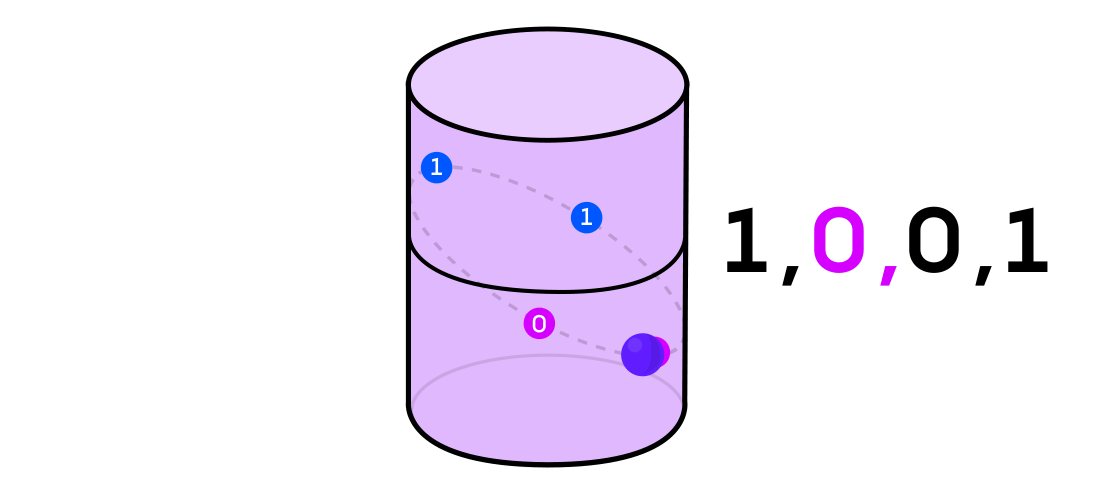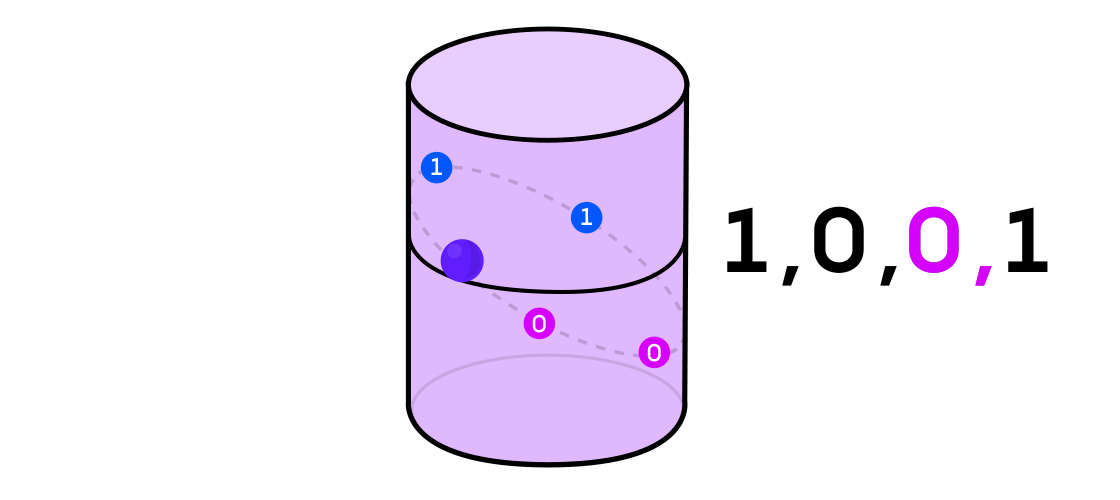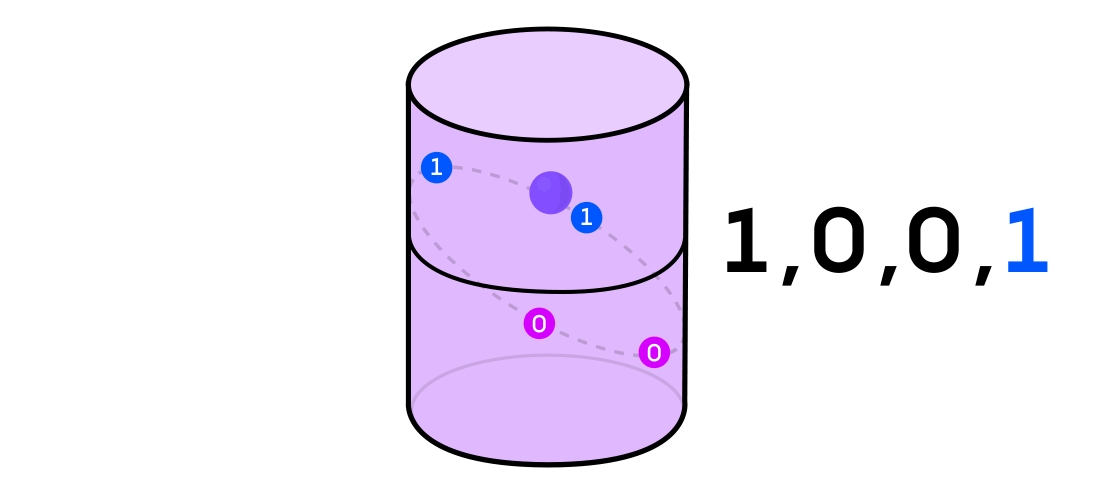
Retornando ao exemplo de um sistema dinâmico em um cilindro, se o ponto estiver em uma parte do cilindro, você indica o valor de saída do sistema 1 e, por outro, em 0.
Austin analisou essas seqüências binárias usando uma ferramenta de
teoria da informação chamada
Hamming Cubes . Imagine um cubo de vértices conectados por arestas. Os números binários são atribuídos a cada vértice - digamos, 001 ou 101. Cada vez que você muda de um vértice para outro, um dos três dígitos é alterado.
Cubos de Hamming podem ser muito mais complicados que os nossos, eles podem ter mais arestas e vértices em mais dimensões que três - mas todos eles têm a propriedade, devido à qual a distância entre dois vértices - ou o número de arestas que você precisa seguir ir de um vértice para outro é igual ao número de lugares em que as linhas de informação correspondentes a esses vértices são distinguidas. Portanto, 000 está localizado à distância de uma aresta de 001, duas arestas de 011 e três de 111.

Para isolar os elementos aleatórios e determinísticos que compõem um sistema dinâmico complexo, Austin pensou na frequência com que um sistema dinâmico pode produzir uma determinada sequência de zeros e zeros representados em um cubo de Hamming. Ele provou que essas seqüências são distribuídas em um cubo de uma certa maneira. Eles se acumulam em um pequeno número de sub-regiões de cubos - e esse cluster reflete o determinismo do sistema - no entanto, são distribuídos aleatoriamente entre as sequências dentro desses clusters, o que reflete a aleatoriedade do sistema.
Essa rotatória era necessária para resolver um problema que não cedia aos ataques diretos.
"O que me surpreendeu não foi tanto a verdade ou a falsidade da hipótese fraca de Pinsker, mas como acabou provando, porque essa tarefa parecia tão insidiosa", disse Lewis Bowen, matemático da Universidade do Texas em Austin. "Antes que as evidências aparecessem, em geral não tínhamos idéia se isso poderia ser feito."
O resultado de Austin fornece a estrutura básica a uma ampla gama de sistemas dinâmicos. Para os matemáticos, que geralmente giram em objetos que parecem interconectados, não está claro como a prova fornece sua geografia exata. Agora eles têm um guia para esses sistemas dinâmicos, embora ainda não se saiba a que tipo de descobertas isso levará.
"Os matemáticos estão sempre interessados nos elementos que compõem qualquer coisa", disse Lindsay. "A prova de Austin é um excelente resultado, que provavelmente terá muitas aplicações em matemática pura, mas não sei dizer o que serão."