🎢 🌅 🤹🏽 Análise wavelet. Parte 3 🤰🏿 👩🏾‍🔬 🕒

1. Introdução

Ao realizar a análise CWT usando a biblioteca PyWavelets (um software de código aberto gratuito lançado sob a licença MIT), há problemas com a visualização do resultado. O programa de teste de visualização proposto pelos desenvolvedores é mostrado na lista a seguir:

Listagem

import pywt import numpy as np import matplotlib.pyplot as plt t = np.linspace(-1, 1, 200, endpoint=False) sig = np.cos(2 * np.pi * 7 * t) + np.real(np.exp(-7*(t-0.4)**2)*np.exp(1j*2*np.pi*2*(t-0.4))) widths = np.arange(1, 31) cwtmatr, freqs = pywt.cwt(sig, widths, 'cmor1-1.5') plt.imshow(cwtmatr, extent=[-1, 1, 1, 31], cmap='PRGn', aspect='auto', vmax=abs(cwtmatr).max(), vmin=-abs(cwtmatr).max()) # doctest: +SKIP plt.show() # doctest: +SKIP

Ao trabalhar com wavelets complexas, por exemplo com 'cmor1-1.5', o programa produz um erro:

 File"C:\Users\User\AppData\Local\Programs\Python\Python36\lib\site-packages\matplotlib\image.py", line 642, in set_data raise TypeError("Image data cannot be converted to float") TypeError: Image data cannot be converted to float

Esse erro, além de dificuldades na escolha da escala (larguras) para fornecer a resolução de tempo necessária, dificulta, principalmente para usuários iniciantes, o estudo da análise CWT, o que me levou a escrever este artigo de natureza educacional.

O objetivo desta publicação é considerar o uso do novo módulo de visualização do escalograma para a análise de sinais simples e especiais, bem como ao usar métodos de normalização, escala logarítmica e síntese, que fornecem informações adicionais na análise de séries temporais.

O artigo utilizou informações da publicação “Uma introdução suave à wavelet para análise de dados” . Nas listagens de exemplos mostrados na publicação, os erros são corrigidos e cada listagem do exemplo é trazida para sua forma finalizada, o que permite usá-lo sem se familiarizar com os anteriores. Para análise wavelet de sinais especiais, foram utilizados dados do banco de dados de amostras PyWavelets.

Um escalograma de wavelet é uma representação bidimensional de dados unidimensionais. O tempo é plotado no eixo X e uma escala é mostrada no eixo Y - o resultado da transformação wavelet do sinal correspondente à amplitude do sinal no tempo X. O valor analítico de uma exibição gráfica do sinal é que a resolução do tempo é exibida no eixo Y, o que fornece informações adicionais sobre as propriedades dinâmicas do sinal.

Wavelet - Escalogramas simples de sinais

1. Onda cosseno com um envelope gaussiano (substituindo wavelets. Você pode estudar a dependência da resolução do tempo na escala):

Listagem

 from numpy import* from pylab import* import scaleogram as scg import pywt #  ,        #       'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #    1  /  ns = 1024 time =arange(ns) scales = scg.periods2scales( arange(1, 40) ) p1=10; periodic1 = cos(2*pi/p1*time) * exp(-((time-ns/2)/200)**2) fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9)); lines = ax1.plot(periodic1); ax1.set_xlim(0, len(time)) ax1.set_title("   ") fig1.tight_layout() ax2 = scg.cws(periodic1, scales=scales, figsize=(6.9,2.9)); txt = ax2.annotate("p1=%s"%p1, xy=(100, 10), bbox=dict(boxstyle="round4", fc="w")) tight_layout() print("    :", scg.get_default_wavelet(), "(", pywt.ContinuousWavelet(scg.get_default_wavelet()).family_name, ")") show()

Função wavelet para conversão de sinal: cmor1-1.5 (wavelets complexas de Morlet)

O sinal periódico aparece agora como uma faixa contínua horizontal no ponto Y = p1, cuja intensidade varia dependendo da amplitude do sinal periódico.

Há alguma imprecisão na detecção, uma vez que a largura de banda não é igual a zero, isso se deve ao fato de as wavelets não detectarem uma frequência, mas sim uma banda. Esse efeito está associado à largura de banda da wavelet.

2. Três pulsos são adicionados seqüencialmente com um período crescente (para considerar variações periódicas em diferentes escalas: análise de resolução múltipla):

Listagem

 from numpy import* import pandas as pd from pylab import* import scaleogram as scg #          #       'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) pulses = zeros(ns, dtype=float32) steps = linspace(0, ns, 8) periods = [10, 20, 40] for i in range(0,3): step_mask = (time > steps[i*2+1]) & (time < steps[i*2+2]) pulses += cos(2*pi/periods[i]*time) * step_mask fig1, ax1 = subplots(1, 1, figsize=(7,3)); lines = ax1.plot(pulses); ax1.set_xlim(0, len(time)); ax1.set_title("     "); ax1.set_xlabel("Time") fig1.tight_layout() ax2 = scg.cws(pulses, scales=scales, figsize=(7,3)) for i in range(0, 3): txt = ax2.annotate("p%d=%ds"%(i+1,periods[i]), xy=(steps[i*2]+20, periods[i]), bbox=dict(boxstyle="round4", fc="w")) ax2.plot(steps[i*2+1]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5) ax2.plot(steps[i*2+2]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5) tight_layout() show()

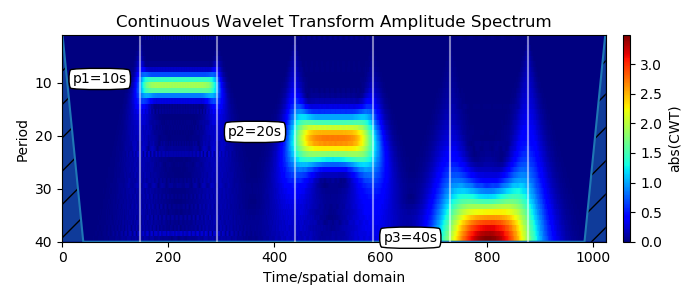
Os impulsos aparecem no local esperado Y, correspondendo à sua periodicidade, estão localizados em frequência e tempo. O começo da tira e o fim correspondem ao pulso.
A largura de banda é escalada com a duração do período. Essa é uma propriedade bem conhecida da transformação wavelet: quando a escala aumenta, a resolução do tempo diminui. Isso também é conhecido como o compromisso entre tempo e frequência. Quando você olha para um espectrograma desse tipo, faz muita análise de resolução.

3. Três oscilações periódicas de diferentes frequências ao mesmo tempo (Wavelet - a análise é capaz de distinguir componentes de sinal por frequências se suas diferenças forem significativas):

Listagem

 from numpy import* import pandas as pd from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) allwaves = np.zeros(ns, dtype=np.float32) periods = [10, 20, 40] for i in range(0,3): allwaves += cos(2*np.pi/periods[i]*time) fig1, ax1 = subplots(1, 1, figsize=(6.5,2)); lines = ax1.plot(allwaves); ax1.set_title("  ") ax1.set_xlim(0, len(time)); ax1.set_xlabel("") fig1.tight_layout() ax2 = scg.cws(allwaves, scales=scales, figsize=(7,2)) tight_layout() show()

4. Sinal periódico não sinusoidal (Considera-se a diferença nas transformações de wavelets de um sinal de onda triangular com um período de 30 segundos em relação aos considerados anteriormente):

Listagem

 from numpy import* from pylab import* import scipy.signal import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) ptri = 30.0 # period in samples raising = 0.8 # fraction of the period raising triangle = scipy.signal.sawtooth(time/ptri*2*pi, raising) # plot the signal fig1, ax1 = subplots(1, 1, figsize=(7,3)); lines = ax1.plot(triangle); ax1.set_xlim(0, len(time)) ax1.set_title("triangle wave increasing 80% of the time with a 30s period") fig1.tight_layout() # and the scaleogram ax2 = scg.cws(triangle, scales=scales, figsize=(7,3)); txt = ax2.annotate("first harmonic", xy=(100, 30), bbox=dict(boxstyle="round4", fc="w")) txt = ax2.annotate("second harmonic", xy=(100, 15), bbox=dict(boxstyle="round4", fc="w")) tight_layout() show()

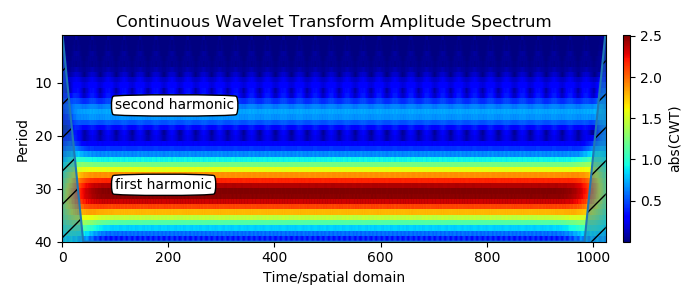
Uma banda grande é o primeiro harmônico. O segundo harmônico é visível exatamente pela metade do valor do período do primeiro harmônico. Este é o resultado esperado para sinais não sinusoidais periódicos. Elementos verticais nebulosos aparecem ao redor do segundo harmônico, que é mais fraco e tem uma amplitude 1/4 do primeiro para uma forma de onda triangular.

5. Impulsos suaves (gaussianos) são semelhantes a estruturas de dados reais. (Este exemplo mostra como usar a análise wavelet para detectar alterações de sinal localizadas ao longo do tempo):

Uma série de pulsos suaves com diferentes valores de sigma:

$2 \ cdot \ sigma _ {1} = 2$
$2 \ cdot \ sigma _ {2} = 10$
$2 \ cdot \ sigma _ {3} = $ 2$

Largura de pulso:

$\ omega _ {1} = 2$
$\ omega _ {2} = $ 2$
$\ omega _ {3} = $ 10$

Listagem

 from numpy import* from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) #       s1=1; s2=5; s3=10 events = [ns*0.1, ns*0.3, ns*0.7] bumps = exp(-((time-events[0])/s1)**2) + exp(-((time-events[1])/s2)**2) + \ exp(-((time-events[2])/s3)**2) #      w1=1; w2=5; w3= 50 steps = ((time > events[0]-w1) & (time < events[0]+w1)) + \ ((time > events[1]-w2) & (time < events[1]+w2)) + \ ((time > events[2]-w3) & (time < events[2]+w3)) #   fig1, (ax1, ax2) = subplots(1, 2, figsize=(11, 2)); ax1.set_title("Bumps"); ax2.set_title("Steps") lines = ax1.plot(bumps); ax1.set_xlim(0, len(time)) lines = ax2.plot(steps); ax2.set_xlim(0, len(time)) fig1.tight_layout() #   scales_bumps = scg.periods2scales(arange(1, 120, 2) ) fig2, (ax3, ax4) = subplots(1, 2, figsize=(14,3)); ax3 = scg.cws(bumps, scales=scales_bumps, ax=ax3) ax4 = scg.cws(steps, scales=scales_bumps, ax=ax4) for bmpw, stepw in [(2*s1, 2*w1), (2*s2,2*w2), (2*s3, 2*w3)]: ax3.plot(ax3.get_xlim(), bmpw*ones(2), 'w-', alpha=0.5) ax4.plot(ax4.get_xlim(), stepw*ones(2), 'w-', alpha=0.5) fig2.tight_layout() show()

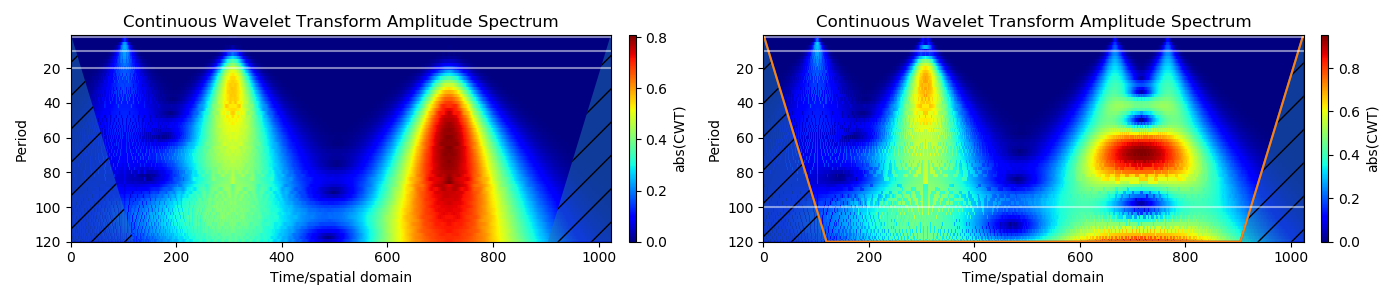
Pulsos discretos criam estruturas cônicas no sialograma, também conhecidas como cone de influência. Impulsos suaves (gaussianos) são semelhantes a estruturas de dados reais e criam cones expandindo-se em direção a grandes escalas. As linhas de orientação horizontais correspondem aproximadamente a períodos de tempo (2 s, 10 s, 20 s). Portanto, o pulso é semelhante a um sinal periódico com um período.

6. Ruído (exibir ruído no sialograma):

Listagem

 from numpy import* from pylab import* import scaleogram as scg import random scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #    1  /  ns = 1024 time =arange(ns) scales = scg.periods2scales( arange(1, 40) ) noise =random.sample(range(ns), ns) fig1, ax1 = plt.subplots(1, 1, figsize=(6.2,2)); ax1.set_title("  ") lines = ax1.plot(time, noise) ax1.set_xlim(0, ns) fig1.tight_layout() ax2 = scg.cws(noise, scales=scales, figsize=(7,2)) tight_layout() show()

O ruído geralmente é exibido como um conjunto de elementos e algumas irregularidades podem parecer objetos de dados reais; portanto, ao usar dados reais, você deve ter cuidado e, se necessário, verificar o nível de ruído. A programação superior será diferente cada vez que o programa for iniciado.

Escalogramas Wavelet de Sinais Especiais

O banco de dados PyWavelets contém vinte sinais especiais de transformação de wavelets que serão úteis para estudo e desenvolvimento. Portanto, darei uma lista que permite realizar uma análise wavelet de todos os vinte sinais:

Listagem

 #!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np from pylab import* import scaleogram as scg import pywt signals = pywt.data.demo_signal('list') signal_length=1024 for signal in signals: if signal in ['Gabor', 'sineoneoverx']: x = pywt.data.demo_signal(signal) else: x = pywt.data.demo_signal(signal, signal_length) times=[] signals=[] for time, sig in enumerate(x.real): times.append(time) signals.append(sig) scg.set_default_wavelet('cmor1-1.5') scales = scg.periods2scales( arange(1, 40) ) fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9)); lines = ax1.plot(signals); ax1.set_xlim(0, len(times)) ax1.set_title("%s"%signal) fig1.tight_layout() ax2 = scg.cws(signals, scales=scales, figsize=(6.9,2.9)); tight_layout() show()

Vou dar apenas um resultado da transformação wavelet do sinal Doppler:

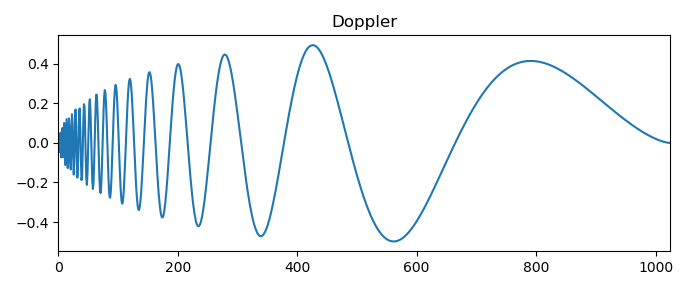
As variedades mais comuns de sinais simples e especiais são consideradas, o que nos permite passar a usar um escalograma para resolver alguns problemas da análise de séries temporais.

Escalogramas da linha do tempo da Wavelet

1. Dados de fertilidade do CDC nos EUA 1969-2008 (os dados de fertilidade contêm características periódicas, tanto em escala anual quanto em menor):

Listagem

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) fig = figure(figsize=(12,2)) lines = plot(births.index, births.values/1000, '-') xlim(datetime_lim) ylabel("Nb of birthes [k]"); title("Total births per day in the US (CDC)"); xlim = xlim() ax = scg.cws(births, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day") set_x_yearly(ax, len(births)) show()

Uma linha horizontal aparece com uma frequência de cerca de 7 dias. Valores altos aparecem perto das bordas da escala, que é o comportamento normal do processamento de wavelets. Esses efeitos são conhecidos como cone de influência, e é por isso que uma máscara (opcional) se sobrepõe a essa área.

2. Normalização (a remoção do valor médio - births_normed = births-births.mean () é obrigatória, caso contrário, os limites dos dados são considerados como estágios que criam muitas detecções falsas em forma de cone):

Listagem

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() ax = scg.cws(births_normed, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day") set_x_yearly(ax, len(births)) show()

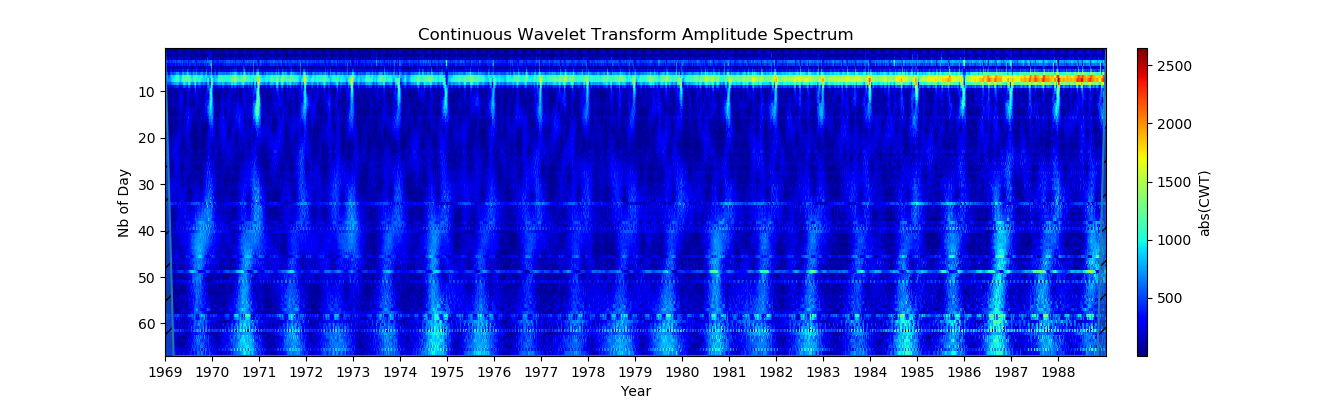
3. Alteração da escala em amplitude (para ver objetos anuais, usando period2scales (), a escala ao longo do eixo Y é especificada).

Listagem

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() scales = scg.periods2scales(np.arange(1, 365+100, 3)) ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 5), xlabel="Year", ylabel="Nb of Day", clim=(0, 2500)) set_x_yearly(ax, len(births)) show()

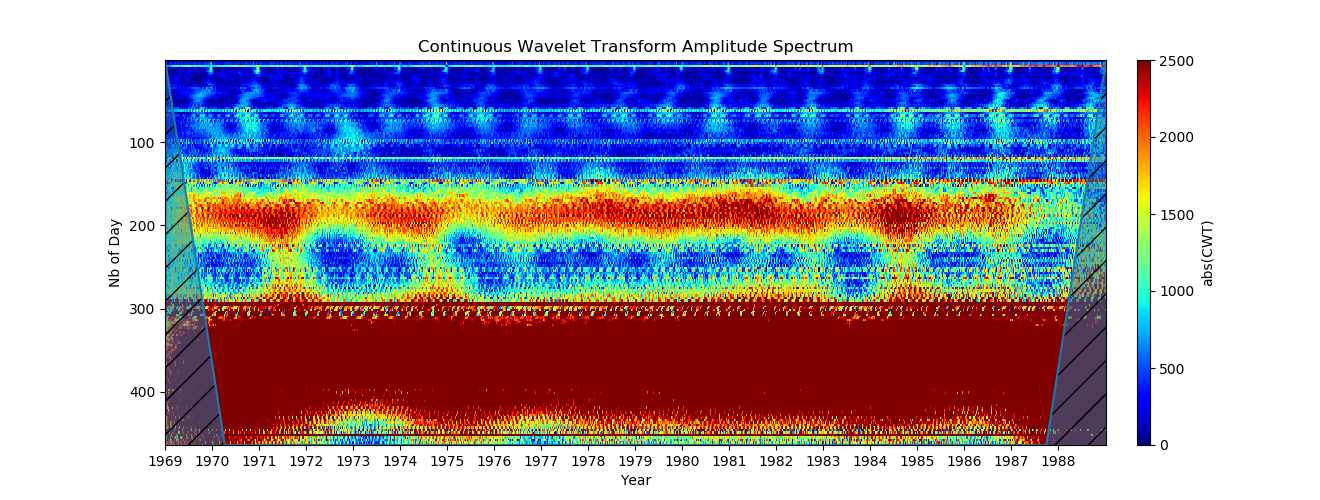
A faixa de amplitude do mapa de cores (eixo Y) agora é definida por clim = (0,2500). O valor exato da amplitude das oscilações depende da wavelet, mas permanecerá próximo da ordem do valor real. Isso é muito melhor, agora vemos muito bem a variação anual, bem como cerca de 6 meses!

4. Usando a escala logarítmica (Para ver períodos pequenos e grandes ao mesmo tempo, é melhor usar a escala logarítmica no eixo Y. Isso é conseguido usando a opção xscale = log.)

Listagem

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() scales = scg.periods2scales(np.arange(1, 365+100, 3)) ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) print("Number of available days:", len(births_normed)) show()

O resultado é muito melhor, mas agora os pixels com baixos valores de períodos são alongados ao longo do eixo Y.

5. Distribuição uniforme em uma escala logarítmica (Para obter uma distribuição uniforme em uma escala, os valores do período devem ser distribuídos uniformemente e depois convertidos em valores da escala, conforme mostrado abaixo :):

Listagem

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #  CWT  ,       cwt = scg.CWT(births_normed, scales=scales) ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) bboxf = dict(boxstyle="round", facecolor="y", edgecolor="0.5") arrowpropsf = dict(facecolor='yellow', shrink=0.05) text = ax.annotate("unusual\nfeature", xy=(365*6, 15), xytext=(365*3, 50), bbox=bboxf, arrowprops=arrowpropsf) show()

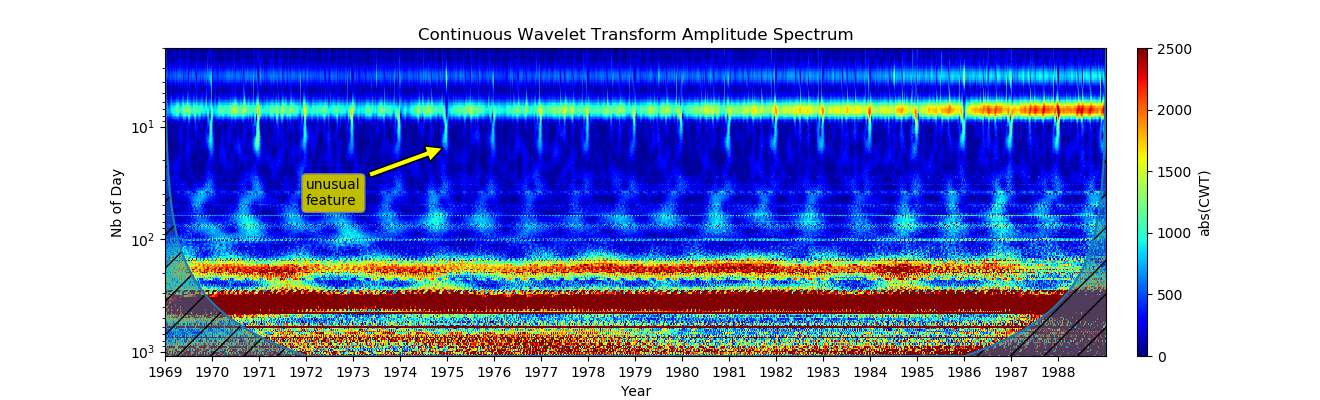
Podemos ver mudanças de sinal em todas as escalas. O sialograma mostra todos os anos em períodos iguais.

6. Destaque parte da linha do tempo (verificação de dados intermediários entre as marcas da linha do tempo em busca de artefatos ou dados ausentes.):

Listagem

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) #    : 1974-1976 fig = figure(figsize=(12,4)) lines =plot(births.index, births.values/1000, '-') xlim(pd.to_datetime("1974-01-01"), pd.to_datetime("1976-01-01")) ylabel("Nb of birthes [k]"); title("Total births per day bw 1974 and 1976"); #      ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) xlim = ax.set_xlim( (1974-1969)*365, (1976-1969)*365 ) show()

, , - , :

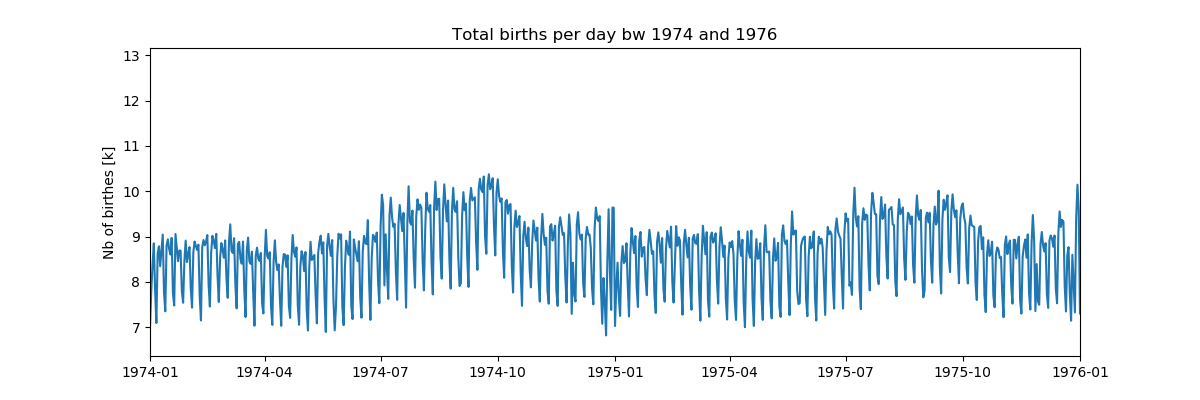
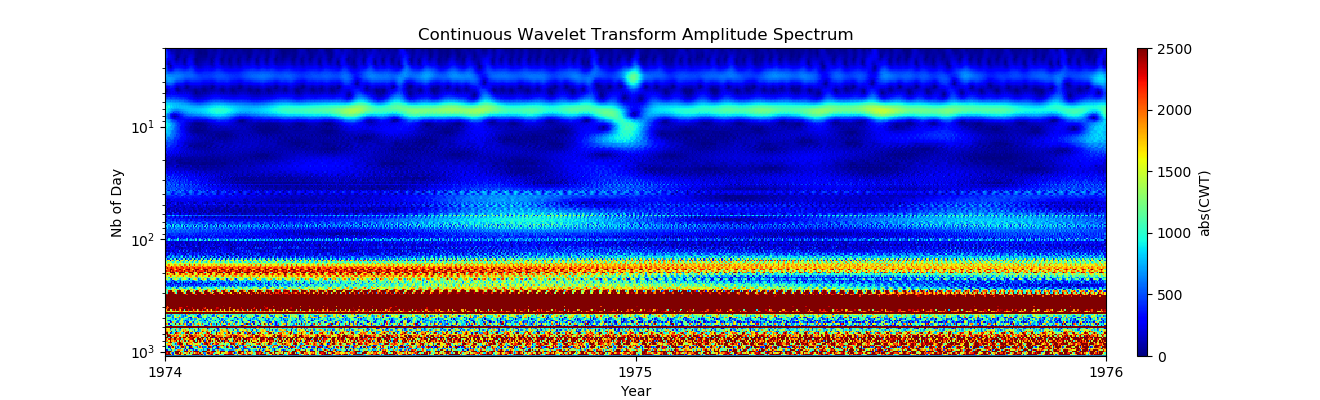
 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) # :  1975    1976  fig = figure(figsize=(12,4)) lines = plot(births.index, births.values/1000, '.-') xlim(pd.to_datetime("1974-12-01"), pd.to_datetime("1975-02-01")) ylabel("Nb of birthes [k]"); title("Total births per day : 2 monthes zoom"); #      ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) xlim = ax.set_xlim( (1975-1969)*365-30, (1975-1969)*365+30 ) show()

, :

: 23/24/25 , ;
, 1- 2- ,

7. ( , ):

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) bbox = dict(boxstyle="round", facecolor="w", edgecolor="0.5") bbox2 = dict(boxstyle="round", facecolor="y", edgecolor="0.5") arrowprops = dict(facecolor='white', shrink=0.05) arrowprops2 = dict(facecolor='yellow', shrink=0.05) for period, label in [ (3.5, "half a week"), (7, "one week"), (365/2, "half a year"), (365, "one year"), (365*2.8, "long trends")]: text = ax.annotate(label, xy=(365*5.5, period), xytext=(365*2, period), bbox=bbox, arrowprops=arrowprops) text = ax.annotate("end of year\neffect", xy=(365*6, 15), xytext=(365*3, 50), bbox=bbox2, arrowprops=arrowprops2) text = ax.annotate("increase in\nvariations *amplitude*", xy=(365*18.5, 7), xytext=(365*14, 50), bbox=bbox2, arrowprops=arrowprops2) show()

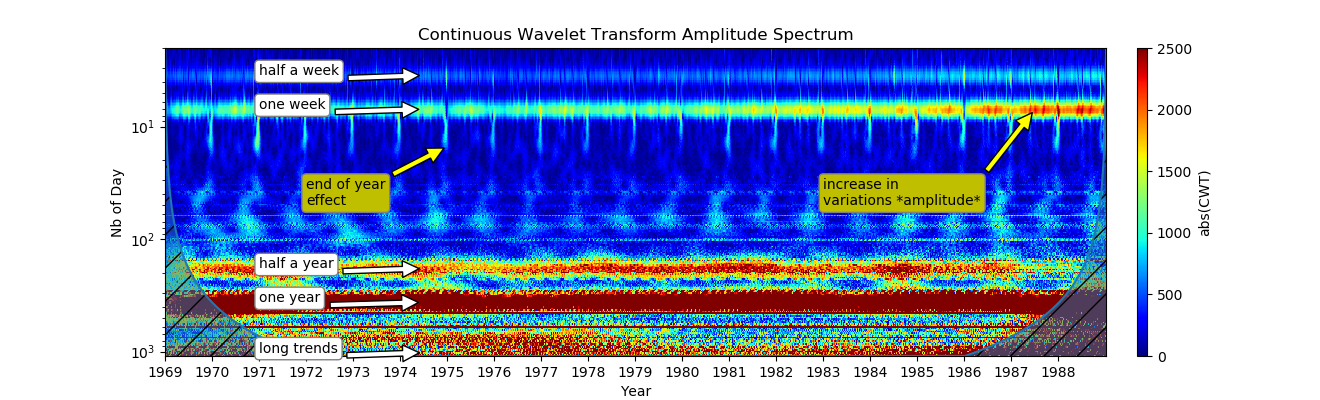
CWT :

, , ;

80- , , ;

— . 3 1 , , . ;

1 . , , .

:

, . , , CWT .

. CWT — , .

, , . – , , mexh gaus5. 1 :

PS :

 >>> import scaleogram; print(scaleogram .__version__) 0.9.5 >>> import pandas; print(pandas .__version__) 0.24.1 >>> import numpy; print(numpy .__version__) 1.16.1 >>> import matplotlib; print(matplotlib .__version__) 3.0.2

*.csv ( ):
year,month,day,gender,births
1969,1,1,F,4046
1969,1,1,M,4440
1969,1,2,F,4454
1969,1,2,M,4548
...
0.24.1 pandas matplotlib.

:

 from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()

Análise wavelet. Parte 3

1. Introdução

Wavelet - Escalogramas simples de sinais

Escalogramas Wavelet de Sinais Especiais

Escalogramas da linha do tempo da Wavelet

:

More articles: