Qual é a melhor ferramenta para desenhar imagens vetoriais? Para mim e provavelmente para muitos outros, a resposta é bastante óbvia: Illustrator ou, talvez, Inkscape. Pelo menos foi o que pensei quando me pediram para desenhar cerca de oitocentos diagramas para um livro de física. Nada de excepcional, apenas um monte de ilustrações em preto e branco com esferas, molas, polias, lentes e assim por diante. Naquele momento, já se sabia que o livro seria produzido no LaTeX e recebi vários documentos do MS Word com imagens incorporadas. Alguns deles eram imagens digitalizadas de outros livros, outros eram desenhos a lápis. Imaginando dias e noites em que escaneei esse material me deixou tonto, tão cedo me vi fantasiando sobre uma solução mais automatizada. Por alguma razão, o
MetaPost se tornou o foco dessas fantasias.
A principal vantagem do uso da solução MetaPost (ou similar) é que toda imagem pode ser uma espécie de função de várias variáveis. Essa imagem pode ser rapidamente ajustada para quaisquer circunstâncias imprevistas do layout, sem interromper importantes relações internas da ilustração (algo com o que realmente me preocupava), o que não é facilmente alcançado com as ferramentas mais tradicionais. Além disso, elementos recorrentes, todas essas esferas e molas, podem ser visualmente mais interessantes do que as ferramentas convencionais permitiriam com as mesmas restrições de tempo.
Eu queria fazer fotos com algum tipo de eclosão, não muito diferente do que você encontra em livros antigos.

Primeiro, eu precisava ser capaz de produzir algumas curvas de espessura variável. A principal complicação aqui é construir uma curva que segue a curva original a uma distância variável. Usei provavelmente o
método de trabalho mais primitivo, que se resume a simplesmente deslocar os segmentos de linha que conectam os pontos de controle da curva de Bezier a uma determinada distância, exceto que essa distância varia ao longo da curva.

Na maioria dos casos, funcionou bem.

Código de exemploA partir daqui, assume-se que a biblioteca é
baixada e
input fiziko.mp; está presente no código MetaPost. O método mais rápido é usar o ConTeXt (então você não precisa de
beginfig e
endfig ):
\starttext
\startMPcode
input fiziko.mp;
% the code goes here
\stopMPcode
\stoptext
ou LuaLaTeX:
\documentclass{article}
\usepackage{luamplib}
\begin{document}
\begin{mplibcode}
input fiziko.mp;
% the code goes here
\end{mplibcode}
\end{document}
beginfig(3);
path p, q; % MetaPost's syntax is reasonably readable, so I'll comment mostly on my stuff
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q := offsetPath(p)(1cm*sin(offsetPathLength*pi)); % first argument is the path itself, second is a function of the position along this path (offsetPathLength changes from 0 to 1), which determines how far the outline is from the original line
draw p;
draw q dashed evenly;
endfig;
Dois contornos podem ser combinados para criar uma linha de contorno para um curso de espessura variável.

Código de exemplobeginfig(4);
path p, q[];
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q1 := offsetPath(p)(1/2pt*(sin(offsetPathLength*pi)**2)); % outline on one side
q2 := offsetPath(p)(-1/2pt*(sin(offsetPathLength*pi)**2)); % and on the other
fill q1--reverse(q2)--cycle;
endfig;
A espessura da linha deve ter um limite inferior; caso contrário, algumas linhas serão muito finas para serem impressas corretamente e isso não parecerá ótimo. Uma das opções (a que eu escolhi) é fazer com que as linhas sejam muito finas, para que a quantidade total de tinta por unidade de comprimento permaneça aproximadamente a mesma que na linha mais fina pretendida. Em outras palavras, em vez de reduzir a quantidade de tinta nas laterais da linha, o algoritmo retira um pouco de tinta da própria linha.

Código de exemplobeginfig(5);
path p;
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
draw brush(p)(1pt*(sin(offsetPathLength*pi)**2)); % the arguments are the same as for the outline
endfig;
Depois de trabalhar com linhas de espessura variável, você pode desenhar esferas. Uma esfera pode ser representada como uma série de círculos concêntricos com as espessuras de linha variando de acordo com a saída de uma função que calcula a luminosidade de um ponto específico da esfera.

Código de exemplobeginfig(6);
draw sphere.c(1.2cm);
draw sphere.c(2.4cm) shifted (2cm, 0);
endfig;
Outro bloco de construção conveniente é um "tubo". Grosso modo, é um cilindro que você pode dobrar. Contanto que o diâmetro seja constante, é bastante direto.

Código de exemplobeginfig(7);
path p;
p := subpath (1,8) of fullcircle scaled 3cm;
draw tube.l(p)(1/2cm); % arguments are the path itself and the tube radius
endfig;
Se o diâmetro não for constante, as coisas ficam mais complicadas: o número de pinceladas deve mudar de acordo com a espessura do tubo, a fim de manter constante a quantidade de tinta por unidade de área antes de levar em consideração as luzes.
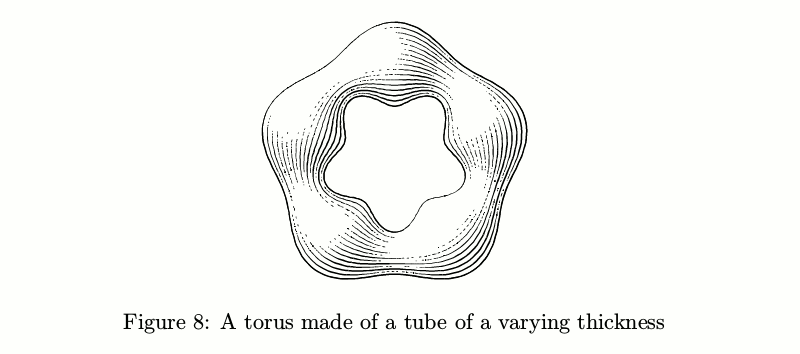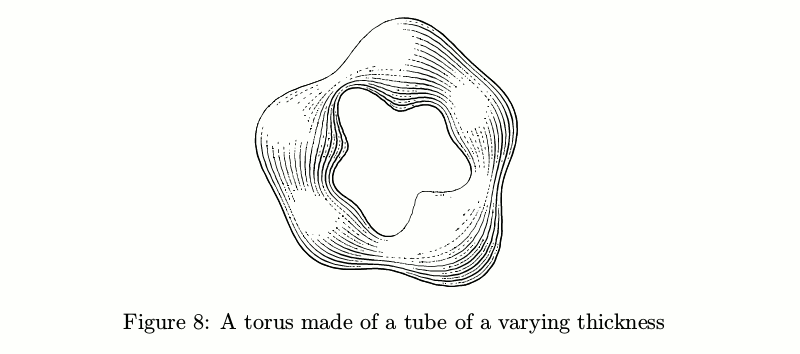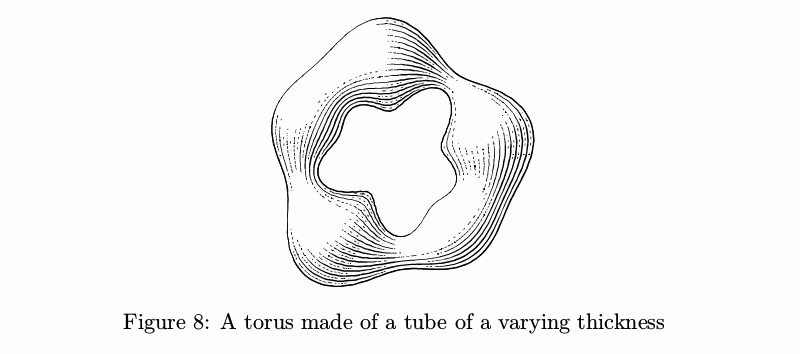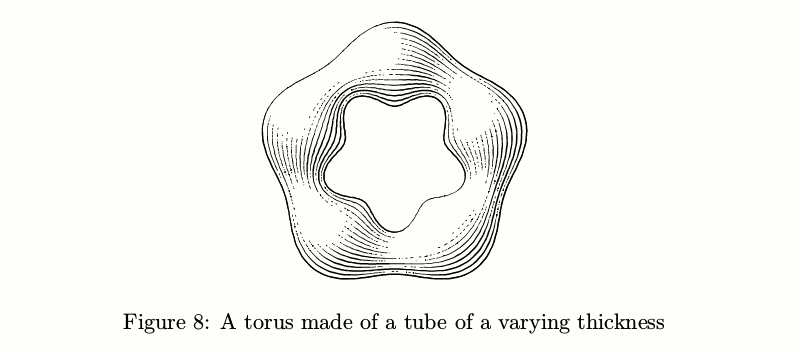
Código de exemplobeginfig(8);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm; % this thing splits every segment between the points of a path (here—fullcircle) into several parts (here—2)
draw tube.l(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
Existem também tubos com hachura transversal. O problema de manter constante a quantidade de tinta acabou sendo ainda mais complicado nesse caso, portanto, muitas vezes esses tubos parecem um pouco desgrenhados.

Código de exemplobeginfig(9);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.t(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
Os tubos podem ser usados para construir uma ampla gama de objetos: de cones e cilindros a balaústres.

Código de exemplobeginfig(10);
draw tube.l ((0, 0) -- (0, 3cm))((1-offsetPathLength)*1cm) shifted (-3cm, 0); % a very simple cone
path p;
p := (-1/2cm, 0) {dir(175)} .. {dir(5)} (-1/2cm, 1/8cm) {dir(120)} .. (-2/5cm, 1/3cm) .. (-1/2cm, 3/4cm) {dir(90)} .. {dir(90)}(-1/4cm, 9/4cm){dir(175)} .. {dir(5)}(-1/4cm, 9/4cm + 1/5cm){dir(90)} .. (-2/5cm, 3cm); % baluster's envelope
p := pathSubdivide(p, 6);
draw p -- reverse(p xscaled -1) -- cycle;
tubeGenerateAlt(p, p xscaled -1, p rotated -90); % a more low-level stuff than tube.t, first two arguments are tube's sides and the third is the envelope. The envelope is basically a flattened out version of the outline, with line length along the x axis and the distance to line at the y. In the case of this baluster, it's simply its side rotated 90 degrees.
endfig;
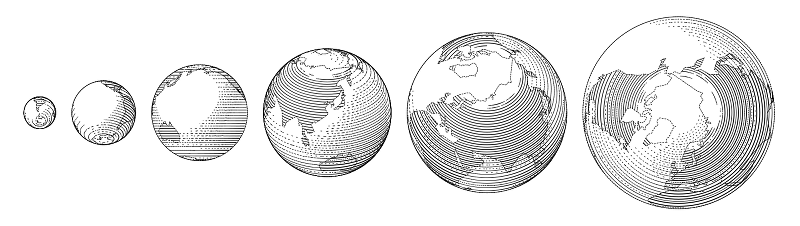
Algumas construções que podem ser feitas a partir dessas primitivas estão incluídas na biblioteca. Por exemplo, o globo é basicamente uma esfera.

Código de exemplobeginfig(11);
draw globe(1cm, -15, 0) shifted (-6/2cm, 0); % radius, west longitude, north latitude, both decimal
draw globe(3/2cm, -30.280577, 59.939461);
draw globe(4/3cm, -140, -30) shifted (10/3cm, 0);
endfig;
No entanto, a hachura aqui é latitudinal e o controle da densidade da linha é muito mais difícil do que nas esferas normais da hachura "concêntrica", portanto é um tipo diferente de esfera.

Código de exemplobeginfig(12);
draw sphere.l(2cm, -60); % diameter and latitude
draw sphere.l(3cm, 45) shifted (3cm, 0);
endfig;
Um peso é uma construção simples feita de tubos de dois tipos.

Código de exemplobeginfig(13);
draw weight.s(1cm); % weight height
draw weight.s(2cm) shifted (2cm, 0);
endfig;
Há também uma ferramenta para amarrar os tubos.

Código de exemplo. Por uma questão de brevidade, apenas um nó.beginfig(14);
path p;
p := (dir(90)*4/3cm) {dir(0)} .. tension 3/2 ..(dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2 ..(dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2 .. cycle;
p := p scaled 6/5;
addStrandToKnot (primeOne) (p, 1/4cm, "l", "1, -1, 1"); % first, we add a strand of width 1/4cm going along the path p to the knot named primeOne. its intersections along the path go to layers "1, -1, 1" and the type of tube is going to be "l".
draw knotFromStrands (primeOne); % then the knot is drawn. you can add more than one strand.
endfig;
Tubos em nós soltam sombras um sobre o outro como deveriam. Em teoria, esse recurso pode ser usado em outros contextos, mas como eu não tinha planos de aprofundar a terceira dimensão, a interface do usuário está um pouco ausente e as sombras funcionam corretamente apenas em alguns objetos.

Código de exemplobeginfig(15);
path shadowPath[];
boolean shadowsEnabled;
numeric numberOfShadows;
shadowsEnabled := true; % shadows need to be turned on
numberOfShadows := 1; % number of shadows should be specified
shadowPath0 := (-1cm, -2cm) -- (-1cm, 2cm) -- (-1cm +1/6cm, 2cm) -- (-1cm + 1/8cm, -2cm) -- cycle; % shadow-dropping object should be a closed path
shadowDepth0 := 4/3cm; % it's just this high above the object on which the shadow falls
shadowPath1 := shadowPath0 rotated -60;
shadowDepth1 := 4/3cm;
draw sphere.c(2.4cm); % shadows work ok only with sphere.c and tube.l with constant diameter
fill shadowPath0 withcolor white;
draw shadowPath0;
fill shadowPath1 withcolor white;
draw shadowPath1;
endfig;
Certamente, você precisará de uma textura de madeira (atualização: desde a publicação da versão em russo deste artigo, o primeiro caso desta biblioteca sendo usado em um projeto real do qual eu sei
que ocorreu , e foi a textura de madeira que veio útil, então isso acabou não sendo uma piada). Como os galhos e seu crescimento afetam o padrão dos anéis do ano é um tópico para alguns estudos sérios. O modelo de trabalho mais simples que eu poderia criar é o seguinte: os anéis do ano são superfícies planas paralelas, distorcidas pelos galhos em crescimento; assim, a superfície é modificada por uma série de "funções de galho" não excessivamente complexas em locais diferentes e as isolinhas da superfície são tomadas como o padrão de toque do ano.

Código de exemplobeginfig(16);
numeric w, b;
pair A, B, C, D, A', B', C', D';
w := 4cm;
b := 1/2cm;
A := (0, 0);
A' := (b, b);
B := (0, w);
B' := (b, wb);
C := (w, w);
C' := (wb, wb);
D := (w, 0);
D' := (wb, b);
draw woodenThing(A--A'--B'--B--cycle, 0); % a piece of wood inside the A--A'--B'--B--cycle path, with wood grain at 0 degrees
draw woodenThing(B--B'--C'--C--cycle, 90);
draw woodenThing(C--C'--D'--D--cycle, 0);
draw woodenThing(A--A'--D'--D--cycle, 90);
eyescale := 2/3cm; % scale for the eye
draw eye(150) shifted 1/2[A,C]; % the eye looks in 150 degree direction
endfig;
O olho da figura acima se abre um pouco ou aperta os olhos e sua pupila também muda de tamanho. Pode não fazer nenhum sentido prático, mas olhos mecanicamente semelhantes apenas parecem chatos.

Código de exemplobeginfig(17);
eyescale := 2/3cm; % 1/2cm by default
draw eye(0) shifted (0cm, 0);
draw eye(0) shifted (1cm, 0);
draw eye(0) shifted (2cm, 0);
draw eye(0) shifted (3cm, 0);
draw eye(0) shifted (4cm, 0);
endfig;
Na maioria das vezes, as ilustrações não eram tão complexas, mas uma abordagem mais rigorosa exigiria a solução de muitos dos problemas do livro para ilustrá-los corretamente. Digamos, o problema da polia de L'Hôpital (não estava naquele livro, mas de qualquer maneira): na corda com o comprimento
suspenso no ponto
uma polia está pendurada; está preso a outra corda, suspensa no ponto
com o peso
no seu fim. A questão é: para onde vai o peso se a polia e as cordas não pesam nada? Surpreendentemente, a solução e a construção para esse problema não são tão simples. Mas, ao brincar com várias variáveis, você pode fazer a imagem parecer perfeita para a página, mantendo a precisão.

Código de exemplovardef lHopitalPulley (expr AB, l, m) = % distance AB between the suspension points of the ropes and their lengths l and m. “Why no units of length?”, you may ask. It's because some calculations inside can cause arithmetic overflow in MetaPost.
save A, B, C, D, E, o, a, x, y, d, w, h, support;
image(
pair A, B, C, D, E, o[];
path support;
numeric a, x[], y[], d[], w, h;
x1 := (l**2 + abs(l)*((sqrt(8)*AB)++l))/4AB; % the solution
y1 := l+-+x1; % second coordinate is trivial
y2 := m - ((AB-x1)++y1); % as well as the weight's position
A := (0, 0);
B := (AB*cm, 0);
D := (x1*cm, -y1*cm);
C := D shifted (0, -y2*cm);
d1 := 2/3cm; d2 := 1cm; d3 := 5/6d1; % diameters of the pulley, weight and the pulley wheel
w := 2/3cm; h := 1/3cm; % parameters of the wood block
o1 := (unitvector(CD) rotated 90 scaled 1/2d3);
o2 := (unitvector(DB) rotated 90 scaled 1/2d3);
E := whatever [D shifted o1, C shifted o1]
= whatever [D shifted o2, B shifted o2]; % pulley's center
a := angle(AD);
support := A shifted (-w, 0) -- B shifted (w, 0) -- B shifted (w, h) -- A shifted (-w, h) -- cycle;
draw woodenThing(support, 0); % wood block everything is suspended from
draw pulley (d1, a - 90) shifted E; % the pulley
draw image(
draw A -- D -- B withpen thickpen;
draw D -- C withpen thickpen;
) maskedWith (pulleyOutline shifted E); % ropes should be covered with the pulley
draw sphere.c(d2) shifted C shifted (0, -1/2d2); % sphere as a weight
dotlabel.llft(btex $A$ etex, A);
dotlabel.lrt(btex $B$ etex, B);
dotlabel.ulft(btex $C$ etex, C);
label.llft(btex $l$ etex, 1/2[A, D]);
)
enddef;
beginfig(18);
draw lHopitalPulley (6, 2, 11/2); % now you can choose the right parameters
draw lHopitalPulley (3, 5/2, 3) shifted (8cm, 0);
endfig;
E o livro? Infelizmente, quando quase todas as ilustrações e o layout estavam prontos, algo aconteceu e o livro foi cancelado. Talvez por isso, decidi reescrever a maioria das funções da biblioteca original a partir do zero (optei por não usar nenhum código original, que, embora indiretamente, me pagassem) e
colocá-lo no GitHub . Algumas coisas, presentes na biblioteca original, como funções para desenhar carros e tratores, não incluí lá, foram adicionados alguns novos recursos, como nós, por exemplo.
Não é rápido: leva cerca de um minuto para produzir todas as fotos deste artigo com o LuaLaTeX no meu laptop com i5-4200U 1,6 GHz. Um gerador de números pseudo-aleatórios é usado aqui e ali, portanto, duas imagens semelhantes não são absolutamente idênticas (esse é um recurso) e cada execução produz imagens ligeiramente diferentes. Para evitar surpresas, você pode simplesmente definir
randomseed := some number e aproveitar os mesmos resultados a cada corrida.
Muito obrigado ao
dr ord e
Mikael Sundqvist por sua ajuda na versão em inglês deste texto.