ARA: algoritmo para encontrar o número máximo de pontos em uma linha reta

Recentemente, deparei-me com uma tarefa clássica de entrevistas: procurar o número máximo de pontos em uma linha reta (em um plano, coordenadas inteiras). A ideia de pesquisa exaustiva veio imediatamente à minha mente, que tem óbvia complexidade de tempo em O (n ^ 2), mas me pareceu que deveria haver algo mais, pelo menos alguma alternativa em O (n * log (n)) . Depois de meia hora, até algo melhor foi encontrado!



_{Uma declaração mais detalhada do problema com exemplos de entrada e saída está em GeeksForGeeks e LeetCode}

Inicialmente, notei que você pode resolver facilmente o problema apenas para linhas horizontais ou verticais, adicionando o X / Y de cada ponto no dicionário. E qual é a diferença entre as outras linhas? Apenas uma ladeira? .. Mas é corrigível!

Assim, decidi que era possível percorrer toda a lista de pontos várias vezes girando-os. E a solução em O (n) é obtida! Embora com um grande coeficiente. Eu realmente espero não ter inventado uma bicicleta :)

# ***  *** #   #    = 180/ROT_COUNT  # #      12, #  180*4    (6% ), #  180*20   (0% ). # ó    . #     - . ROT_COUNT = 180*10 #  #        , #       1 / MULT_COEF. #    4  . #   MULT_COEF   ROT_COUNT. # ó    - . #     - . MULT_COEF = 2 ** 3 angles = list(map(lambda x: x*180.0/ROT_COUNT, range(ROT_COUNT))) def mnp_rotated(points, angle): """Returns Maximum Number of Points on the same line with given rotation""" #   rad = math.radians(angle) co = math.cos(rad) si = math.sin(rad) #      counts = {} for pair in points: #    nx = pair[0]*co - pair[1]*si #       , #      #       #      nx = int(nx * MULT_COEF) #   if nx in counts: counts[nx] += 1 else: counts[nx] = 1 #    return max(counts.values()) def mnp(points): """Returns Maximum Number of Points on the same line""" res = 0 best_angle = 0 #      for i in angles: current = mnp_rotated(points, i) #  ,     if current > res: res = current best_angle = i return res 

Visualizado, parece algo como isto:
_{meu primeiro GIF caseiro, por favor, não repreenda :)}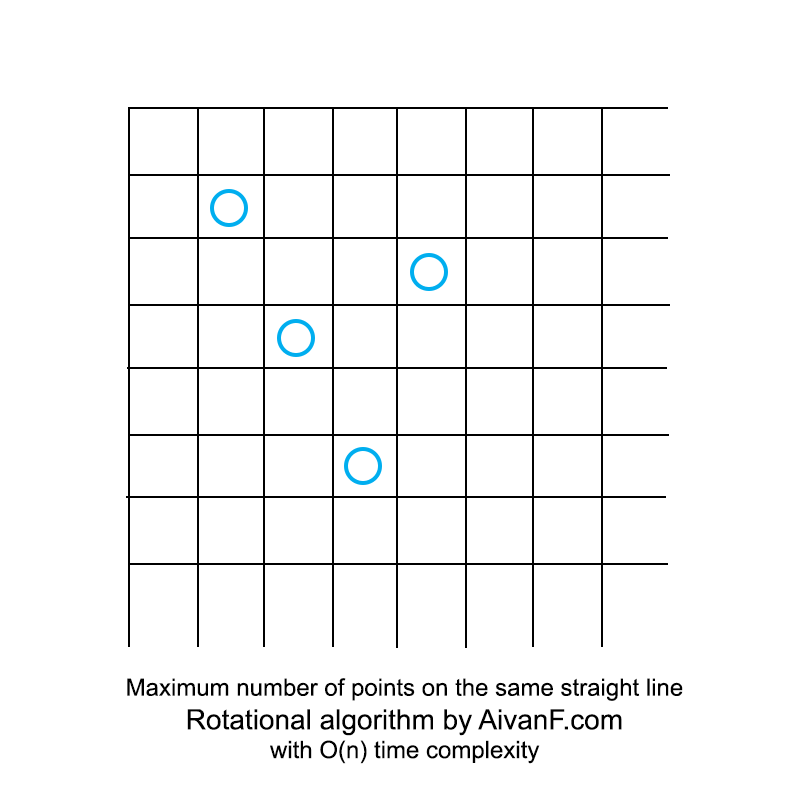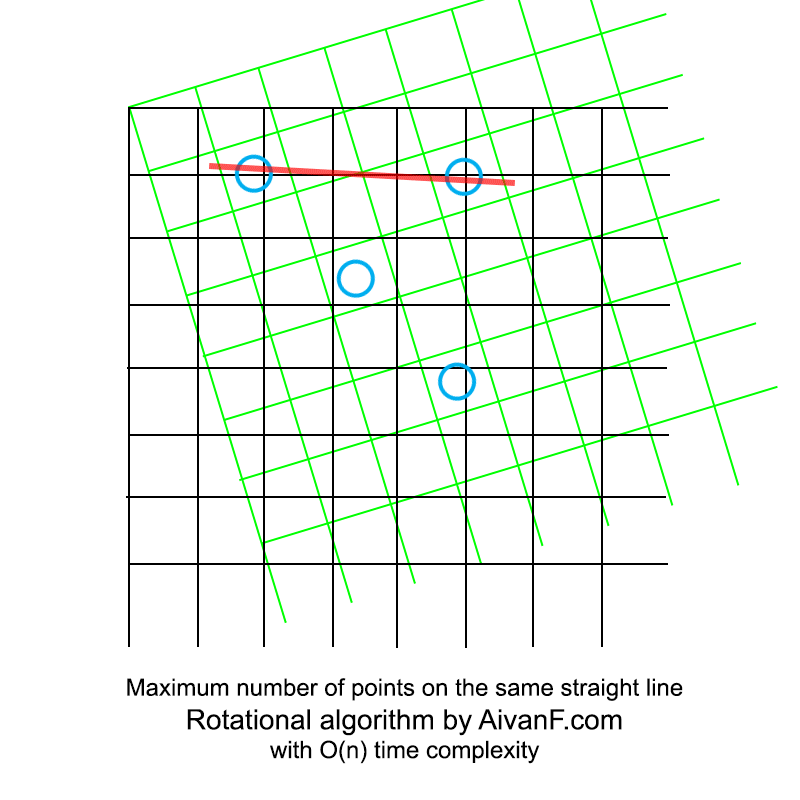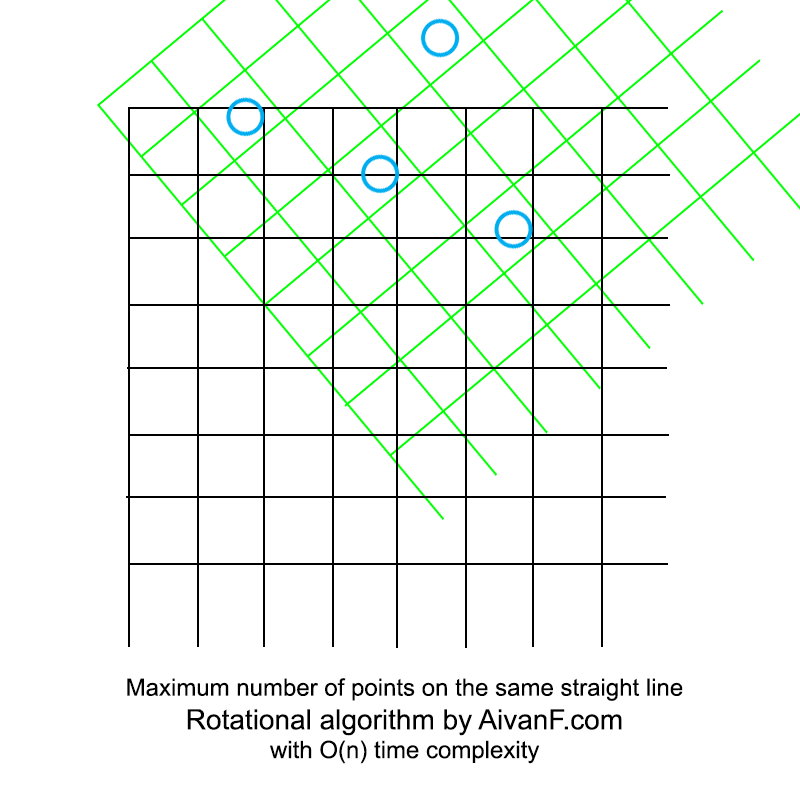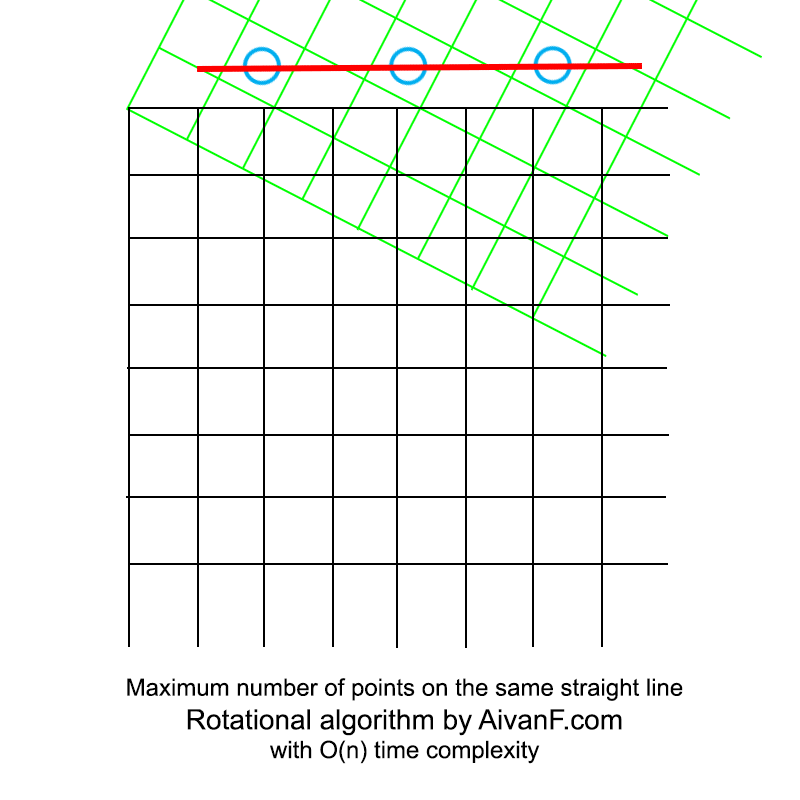



É interessante notar que a implementação subsequente da pesquisa exaustiva ocupou mais linhas de código.

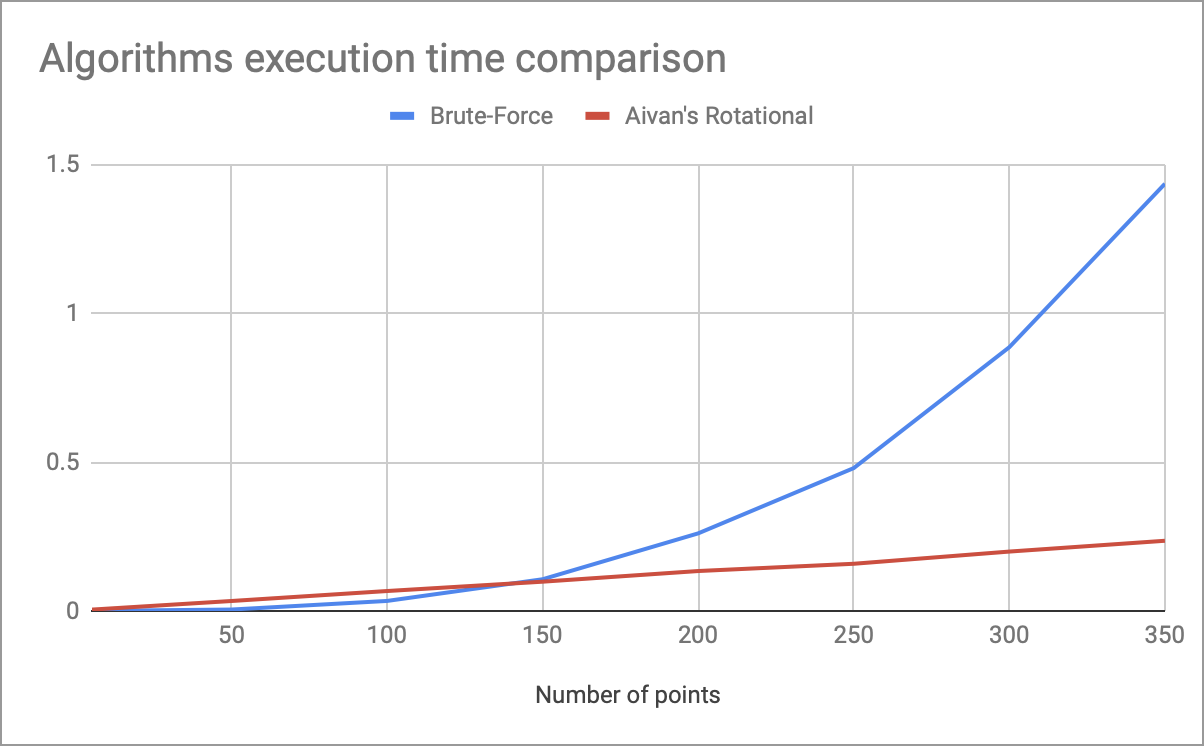
O gráfico com medições do tempo de execução do meu algoritmo rotacional e a enumeração completa, dependendo do número de pontos, está no cabeçalho.


Aproximadamente 150 pontos mostram a vantagem da complexidade linear no tempo (com os coeficientes usados ​​no código acima). Como resultado, esse algoritmo tem as seguintes desvantagens:

• A precisão não é absoluta.
• O tempo de execução em pequenos conjuntos de pontos é longo.
  _{Em geral, isso é facilmente corrigido por uma seleção competente de coeficientes: para conjuntos simples, ROT_COUNT = 36 em vez de 2000 é suficiente, o que acelera o código mais de 50 vezes.}

E essas vantagens:

• Trabalha calmamente com coordenadas fracionárias.
• A complexidade do tempo é linear, o que é perceptível em grandes conjuntos de dados.

Uma tabela com medidas está disponível aqui . Todo o código fonte do projeto, com algoritmos e várias verificações, está no GitHub .

Update Quero observar mais uma vez que esse algoritmo tem vantagens e desvantagens, não o advogo como um substituto ideal para força bruta, acabei de descrever uma alternativa possível interessante, que em alguns casos pode ser mais apropriada.