
Como criar um solucionador de não-programa para Python, reescreva-o no Rust para executá-lo diretamente no navegador através do WebAssembly.
TL; DR
Iniciar
Sobre palavras cruzadas em japonês (nonograms) no Habré já havia várias postagens. Exemplo
e mais um .
As imagens são criptografadas com números localizados à esquerda das linhas e também acima das colunas. O número de números mostra quantos grupos de células pretas (ou suas cores, para palavras cruzadas coloridas) estão na linha ou coluna correspondente e os próprios números - quantas células mescladas cada um desses grupos contém (por exemplo, um conjunto de três números - 4, 1 e 3 significa que nesta linha existem três grupos: o primeiro - de quatro, o segundo - de um, o terceiro - de três células negras). Em palavras cruzadas em preto e branco, os grupos devem ser separados por pelo menos uma célula vazia; nas palavras cruzadas em cores, esta regra se aplica apenas a grupos de uma cor e grupos multicoloridos podem ser espaçados (as células vazias também podem estar nas bordas das linhas). É necessário determinar a localização dos grupos de células.
Um dos pontos de vista mais geralmente aceitos é que palavras cruzadas "corretas" podem ser chamadas apenas daquelas que são resolvidas de maneira "lógica". Isso geralmente é chamado de método de solução, no qual as dependências entre diferentes linhas e / ou colunas não são levadas em consideração. Em outras palavras, uma solução é uma sequência de decisões independentes de linhas ou colunas individuais até que todas as células sejam preenchidas (mais sobre o algoritmo abaixo). Por exemplo, somente esses nonogramas podem ser encontrados no site http://nonograms.org/ ( http://nonograms.ru/ ). Os nonogramas deste site já foram citados como exemplo no artigo Resolvendo palavras cruzadas coloridas em japonês na velocidade da luz . Para fins de comparação e verificação, meu solucionador também adicionou suporte para baixar e analisar palavras cruzadas deste site (obrigado a KyberPrizrak pela permissão para usar materiais de seu site).
No entanto, o conceito de nonogramas pode ser estendido a um problema mais geral, quando o método "lógico" usual leva a um beco sem saída. Nesses casos, é preciso fazer uma suposição sobre a cor de uma célula e, depois de provar que essa cor leva a uma contradição, marcar a cor oposta para essa célula. A sequência de tais etapas pode (se você tiver paciência) nos fornecer todas as soluções. Este artigo abordará principalmente a solução de um caso mais geral de palavras cruzadas.
Python
Cerca de um ano e meio atrás, acidentalmente me deparei com um artigo que descrevia um método para resolver uma única linha (como se viu mais tarde, o método era bastante lento).
Quando implementei esse método no Python (minha principal linguagem de trabalho) e adicionei uma atualização seqüencial de todas as linhas, vi que tudo isso não estava sendo resolvido muito rapidamente. Depois de estudar o material, verificou-se que, neste tópico, existem muitos trabalhos e implementações que oferecem abordagens diferentes para esta tarefa.
Pareceu-me que o trabalho mais ambicioso na análise de várias implementações de solucionadores foi realizado por Jan Wolter, publicando em seu site (que, até onde eu sei, continua sendo o maior repositório público de nonogramas na Internet), um estudo detalhado contendo uma riqueza de informações e links que podem ajudar na criando seu próprio solucionador.
Estudando várias fontes (elas estarão no final do artigo), eu melhorei gradualmente a velocidade e a funcionalidade do meu solucionador. Como resultado, fiquei viciado e participei da implementação, refatoração e depuração de algoritmos por cerca de 10 meses em um tempo livre do trabalho.
Algoritmos principais
O solucionador resultante pode ser representado na forma de quatro níveis de decisão:
solucionador linear ( linha ): na entrada, uma linha de células e uma linha de descrição (pistas); na saída, uma linha parcialmente resolvida. Na solução python, implementei 4 algoritmos diferentes (3 deles são adaptados para palavras cruzadas em cores). O mais rápido acabou sendo o algoritmo BguSolver, nomeado após a fonte original . Este é um método muito eficaz e praticamente padrão para resolver seqüências de caracteres não programadas usando programação dinâmica. O pseudocódigo deste método pode ser encontrado, por exemplo, neste artigo .
( propagação ) colocamos todas as linhas e colunas em uma fila, passamos por isso com um solucionador linear, quando recebemos novas informações ao resolver uma linha (coluna), atualizamos a fila, respectivamente, com novas colunas (linhas). Continue até a linha estar vazia.
Exemplo e códigoTomamos a próxima tarefa a resolver a partir da fila. Seja uma sequência vazia (não resolvida) de comprimento 7 (que a denotamos como ??????? ) com uma descrição dos blocos [2, 3] . O solucionador linear produzirá uma string parcialmente resolvida ?X??XX? onde X é a célula preenchida. Ao atualizar a linha, vemos que as colunas com os números 1, 4, 5 foram alteradas (a indexação começa em 0). Isso significa que novas informações apareceram nas colunas indicadas e podem ser retornadas ao solucionador "linear". Colocamos essas colunas na fila de tarefas com maior prioridade (a fim de fornecê-las ao solucionador linear a seguir).
def propagation(board): line_jobs = PriorityDict() for row_index in range(board.height): new_job = (False, row_index) line_jobs[new_job] = 0 for column_index in range(board.width): new_job = (True, column_index) line_jobs[new_job] = 0 for (is_column, index), priority in line_jobs.sorted_iter(): new_jobs = solve_and_update(board, index, is_column) for new_job in new_jobs:
( análise ) para cada célula não resolvida, classificamos todas as opções de cores e tentamos a propagação com essas novas informações. Se tivermos uma contradição, jogaremos essa cor fora das opções de cores da célula e tentaremos nos beneficiar dela novamente usando propagação. Se for resolvido até o fim, adicionamos a solução à lista de soluções, mas continuamos os experimentos com outras cores (pode haver várias soluções). Se chegarmos a uma situação em que é impossível resolver ainda mais, simplesmente ignoramos e repetimos o procedimento com uma cor / célula diferente.
CódigoRetorna True se uma contradição for recebida como resultado da amostra.
def probe(self, cell_state): board = self.board pos, assumption = cell_state.position, cell_state.color
( retorno ) se, durante a investigação, você não ignora um quebra-cabeça parcialmente resolvido, mas continua invocando recursivamente o mesmo procedimento, obtemos retorno (em outras palavras, uma caminhada completa na profundidade da árvore de decisão em potencial). Aqui, um grande papel começa a desempenhar, qual das células será escolhida como a próxima extensão da solução em potencial. Uma boa pesquisa sobre este tópico está nesta publicação .
CódigoO retorno é bastante confuso comigo, mas essas duas funções descrevem aproximadamente o que acontece durante uma pesquisa recursiva
def search(self, search_directions, path=()): """ Return False if the given path is a dead end (no solutions can be found) """ board = self.board depth = len(path) save = board.make_snapshot() try: while search_directions: state = search_directions.popleft() assumption, pos = state.color, state.position cell_colors = board.cell_colors(pos) if assumption not in cell_colors: LOG.warning("The assumption '%s' is already expired. " "Possible colors for %s are %s", assumption, pos, cell_colors) continue if len(cell_colors) == 1: LOG.warning('Only one color for cell %r left: %s. Solve it unconditionally', pos, assumption) try: self._solve_without_search() except NonogramError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The path %s is invalid", assumption, pos, path) return False if board.is_solved_full: self._add_solution() LOG.warning( "The only color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True continue rate = board.solution_rate guess_save = board.make_snapshot() try: LOG.warning('Trying state: %s (depth=%d, rate=%.4f, previous=%s)', state, depth, rate, path) success = self._try_state(state, path) finally: board.restore(guess_save) if not success: try: LOG.warning( "Unset the color %s for cell '%s'. Solve it unconditionally", assumption, pos) board.unset_color(state) self._solve_without_search() except ValueError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The whole branch (depth=%d) is invalid. ", assumption, pos, depth) return False if board.is_solved_full: self._add_solution() LOG.warning( "The negation of color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True finally:
Portanto, começamos a resolver nossas palavras cruzadas a partir do segundo nível (o primeiro é adequado apenas para o caso degenerado, quando em todas as palavras cruzadas há apenas uma linha ou coluna) e subimos gradualmente os níveis. Como você pode imaginar, cada nível causa o nível subjacente várias vezes; portanto, para uma solução eficaz, é imperativo ter primeiro e segundo níveis rápidos, que podem ser chamados milhões de vezes para quebra-cabeças complexos.
Nesse estágio, verifica-se (bastante esperado) que o python não seja a ferramenta adequada para o desempenho máximo em uma tarefa que exige muita CPU: todos os cálculos são extremamente ineficientes em comparação com as linguagens de nível inferior. Por exemplo, o solucionador de BGU com algoritmos mais próximos (em Java), de acordo com os resultados das medições, mostrou ser 7-17 (às vezes até 27) vezes mais rápido em uma variedade de tarefas.
Mais detalhes pynogram_my BGU_my speedup
Dançarina 0.976 0.141 6.921986
Cat 1.064 0.110 9.672727
Skid 1.084 0.101 10.732673
Bucks 1.116 0.118 9.457627
Edge 1.208 0,094 12,851064
Fumaça 1.464 0.120 12.200000
Nó 1.332 0.140 9.514286
Balanço 1,784 0,138 12,927536
Mãe 2,108 0,147 14,340136
DiCap 2.076 0,176 11,795455
Tragic 2,386 0,265 8,935849
Merka 2.084 0,196 10.632653
Petro 2.948 0.219 13.461187
M&M 3,588 0,375 9,568000
Assinado 4.068 0,242 16.809917
Luz 3.848 0.488 7.885246
Forever 111.000 13.570 8.179808
Center 5.700 0,327 17,431193
Hot 3.150 0.278 11.330935
Karatê 2.500 0.219 11.415525
9-Dom 510.000 70.416 7.242672
Bandeira 149.000 5.628 26.474769
Leão 71.000 2.895 24.525043
Marley 12.108 4.405 2.748695
Coisa 321.000 46.166 6.953169
Natureza inf 433.138 inf
Sierp inf inf NaN
Gettys inf inf NaN
As medições foram realizadas no meu carro, os quebra-cabeças são retirados do conjunto padrão que Jan Wolter usou em sua comparação
E isso já foi depois que eu comecei a usar o PyPy, e no CPython padrão o tempo de cálculo foi maior do que no PyPy 4-5 vezes! Podemos dizer que o desempenho de um solucionador Java semelhante acabou sendo 28-85 vezes maior que o código CPython.
Tentativas de melhorar o desempenho do meu solucionador usando a criação de perfil (cProfile, SnakeViz, line_profiler) levaram a alguma aceleração, mas é claro que elas não deram um resultado estranho.
O + solver pode resolver todos os quebra-cabeças dos sites https://webpbn.com , http://nonograms.org e seu próprio formato (baseado em ini)
+ resolve nonogramas em preto e branco e em cores com qualquer número de cores (o número máximo de cores encontradas é 10)
+ resolve quebra-cabeças com tamanhos de bloco ausentes (manchados). Um exemplo de um quebra-cabeça .
+ pode renderizar quebra-cabeças no console / nas maldições / janela no navegador (ao instalar a opção adicional pynogram-web ). Para todos os modos, é possível visualizar o progresso da solução em tempo real.
- cálculos lentos (em comparação com as implementações descritas na comparação de artigos dos solucionadores, consulte a tabela ).
- retorno ineficiente: alguns quebra-cabeças podem ser resolvidos por horas (quando a árvore de decisão é muito grande).
Ferrugem
No começo do ano, comecei a estudar Rust. Comecei, como sempre, com o livro , aprendi sobre o WASM, passei pelo tutorial proposto . No entanto, eu queria uma tarefa real na qual você possa se engajar nos pontos fortes da linguagem (principalmente sua super performance), e não alguns exemplos inventados por alguém. Então voltei aos nonogramas. Mas agora eu já tinha uma versão funcional de todos os algoritmos em Python, que foi deixada para "apenas" reescrever.
As boas notícias estavam me esperando desde o início: descobriu-se que Rust, com seu sistema de tipos, descreve perfeitamente as estruturas de dados para minha tarefa. Por exemplo, uma das correspondências básicas BinaryColor + BinaryBlock / MultiColor + ColoredBlock permite separar permanentemente os nonogramas em preto e branco e em cores. Se em algum lugar do código tentarmos resolver uma sequência colorida usando blocos de descrição binária comuns, obteremos um erro de compilação sobre incompatibilidade de tipos.
Tipos básicos se parecem com isso pub trait Color { fn blank() -> Self; fn is_solved(&self) -> bool; fn solution_rate(&self) -> f64; fn is_updated_with(&self, new: &Self) -> Result<bool, String>; fn variants(&self) -> Vec<Self>; fn as_color_id(&self) -> Option<ColorId>; fn from_color_ids(ids: &[ColorId]) -> Self; } pub trait Block { type Color: Color; fn from_str_and_color(s: &str, color: Option<ColorId>) -> Self { let size = s.parse::<usize>().expect("Non-integer block size given"); Self::from_size_and_color(size, color) } fn from_size_and_color(size: usize, color: Option<ColorId>) -> Self; fn size(&self) -> usize; fn color(&self) -> Self::Color; } #[derive(Debug, PartialEq, Eq, Hash, Clone)] pub struct Description<T: Block> where T: Block, { pub vec: Vec<T>, }
Ao portar o código, alguns pontos indicaram claramente que uma linguagem de tipo estaticamente como Rust (bem, ou, por exemplo, C ++) é mais adequada para esta tarefa. Mais precisamente, genéricos e características descrevem um domínio melhor do que hierarquias de classe. Portanto, no código Python, eu tinha duas classes para um BguSolver linear, BguSolver e BguColoredSolver que resolviam uma linha em preto e branco e uma linha de cores, respectivamente. No código Rust, ainda tenho a única struct DynamicSolver<B: Block, S = <B as Block>::Color> genérica struct DynamicSolver<B: Block, S = <B as Block>::Color> , que pode resolver os dois tipos de tarefas, dependendo do tipo passado durante a criação ( DynamicSolver<BinaryBlock>, DynamicSolver<ColoredBlock> ). Isso, é claro, não significa que algo semelhante não possa ser feito em Python, apenas no Rust o sistema de tipos claramente indicado para mim: se você não fosse por esse caminho, teria que escrever uma tonelada de código repetido.
Além disso, quem tentou escrever no Rust, sem dúvida percebeu o efeito da "confiança" no compilador, quando o processo de escrever código é reduzido ao seguinte algoritmo pseudo-meta:
write_initial_code
while (compiler_hints = $ (verificação de carga))! = 0; fazer
fix_errors (dicas do compilador)
fim
Quando o compilador parar de emitir erros e avisos, seu código será consistente com o sistema de tipos e com o verificador de empréstimos e você avisará antecipadamente a ocorrência de vários bugs em potencial (é claro, sujeitos a um design cuidadoso dos tipos de dados).
Vou dar alguns exemplos de funções que mostram como o código Rust pode ser conciso (em comparação com os equivalentes do Python).
unsolved_neighboursFornece uma lista de "vizinhos" não resolvidos para um determinado ponto (x, y)
def unsolved_neighbours(self, position): for pos in self.neighbours(position): if not self.is_cell_solved(*pos): yield pos
fn unsolved_neighbours(&self, point: &Point) -> impl Iterator<Item = Point> + '_ { self.neighbours(&point) .into_iter() .filter(move |n| !self.cell(n).is_solved()) }
parcial_sumsPara um conjunto de blocos descrevendo uma linha, forneça somas parciais (levando em consideração as lacunas necessárias entre os blocos) Os índices resultantes indicarão a posição mínima na qual o bloco pode terminar (essas informações serão usadas posteriormente para um solucionador linear).
Por exemplo, para esse conjunto de blocos [2, 3, 1] , temos a saída [2, 6, 8] , o que significa que o primeiro bloco pode ser deslocado ao máximo para a esquerda, de modo que sua borda direita ocupe a 2ª célula, da mesma forma que o resto blocos:
1 2 3 4 5 6 7 8 9
_ _ _ _ _ _ _ _ _ _
2 3 1 | _ | _ | _ | _ | _ | _ | _ | _ | _ |
^ ^ ^
| | |
fim de 1 bloco | | |
fim do bloco 2 -------- |
fim do bloco 3 ------------
@expand_generator def partial_sums(blocks): if not blocks: return sum_so_far = blocks[0] yield sum_so_far for block in blocks[1:]: sum_so_far += block + 1 yield sum_so_far
fn partial_sums(desc: &[Self]) -> Vec<usize> { desc.iter() .scan(None, |prev, block| { let current = if let Some(ref prev_size) = prev { prev_size + block.0 + 1 } else { block.0 }; *prev = Some(current); *prev }) .collect() }
Ao portar, fiz várias alterações
Ferramentas úteis
- O clippy é um analisador estático padrão que às vezes pode até dar dicas, aumentando ligeiramente o desempenho do código.
- O valgrind é uma ferramenta para análise dinâmica de aplicativos. Usei-o como um criador de perfil para procurar botneks (
valrgind --tool=callgrind ) e, particularmente, seções de código valrgind --tool=massif memória ( valrgind --tool=massif ). Dica: defina [profile.release] debug = true para Cargo.toml antes de iniciar o criador de perfil. Isso deixará os caracteres de depuração no executável. - kcachegrind para visualizar arquivos de callgrind. Uma ferramenta muito útil para encontrar os lugares mais problemáticos em termos de desempenho.
Desempenho
Que para que reescrita em Rust foi iniciada. Pegamos as palavras cruzadas da tabela de comparação já mencionada e as executamos nos melhores solucionadores descritos no artigo original. Resultados e descrição das execuções aqui . Pegamos o arquivo resultante e construímos alguns gráficos: como o tempo de solução varia de milissegundos a dezenas de minutos, o gráfico é feito com uma escala logarítmica.
executar no laptop jupyter import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline
solucionador de python
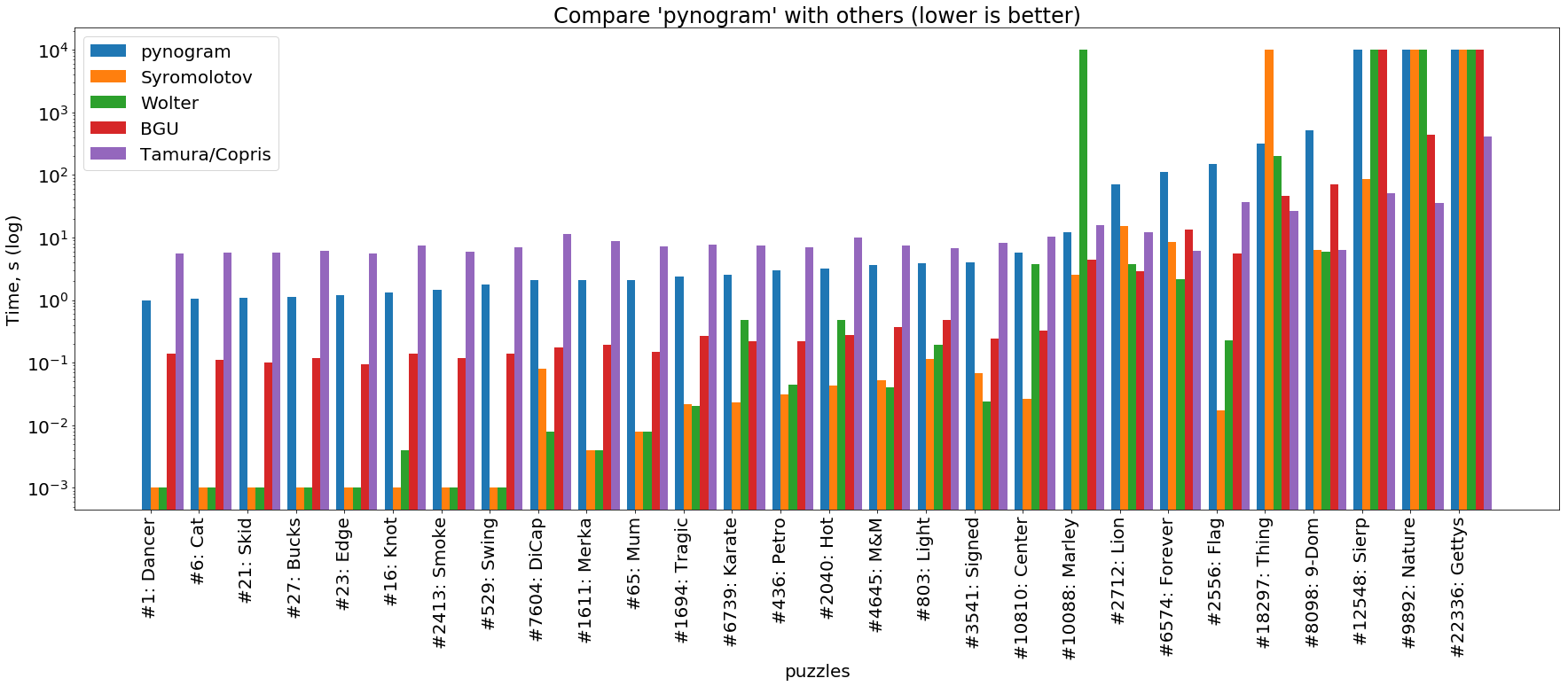
(a imagem é clicável )
Vemos que o picograma aqui é mais lento que todos os solucionadores apresentados. A única exceção a essa regra é o solucionador Tamura / Copris baseado no SAT, que resolve os quebra-cabeças mais simples (a parte esquerda do gráfico) por mais tempo que o nosso. No entanto, esse é um recurso dos solucionadores SAT: eles são projetados para palavras cruzadas super complexas nas quais um solucionador regular fica preso no retorno por um longo tempo. Isso é claramente visível no lado direito do gráfico, onde Tamura / Copris resolve os quebra-cabeças mais difíceis dezenas e centenas de vezes mais rápido que todos os outros.
solucionador de ferrugem
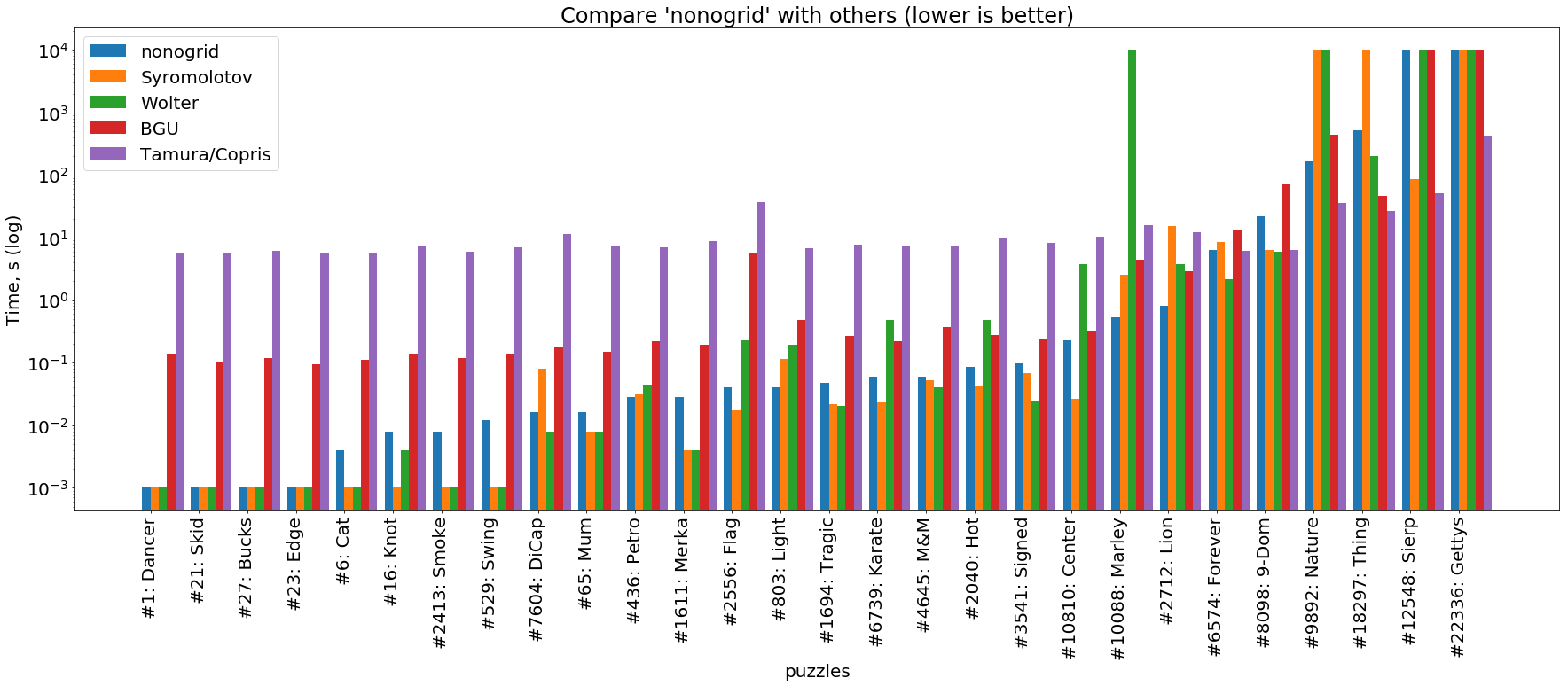
(a imagem é clicável )
Este gráfico mostra que a não grade em tarefas simples também lida com ou um pouco pior que os solucionadores de alto desempenho escritos em C e C ++ ( Wolter e Syromolotov ). Com a complicação das tarefas, nosso solucionador repete aproximadamente a trajetória do solucionador de BGU (Java), mas quase sempre à frente dele em cerca de uma ordem de magnitude. Nas tarefas mais difíceis, Tamura / Copris está sempre à frente de todos.
ferrugem vs python
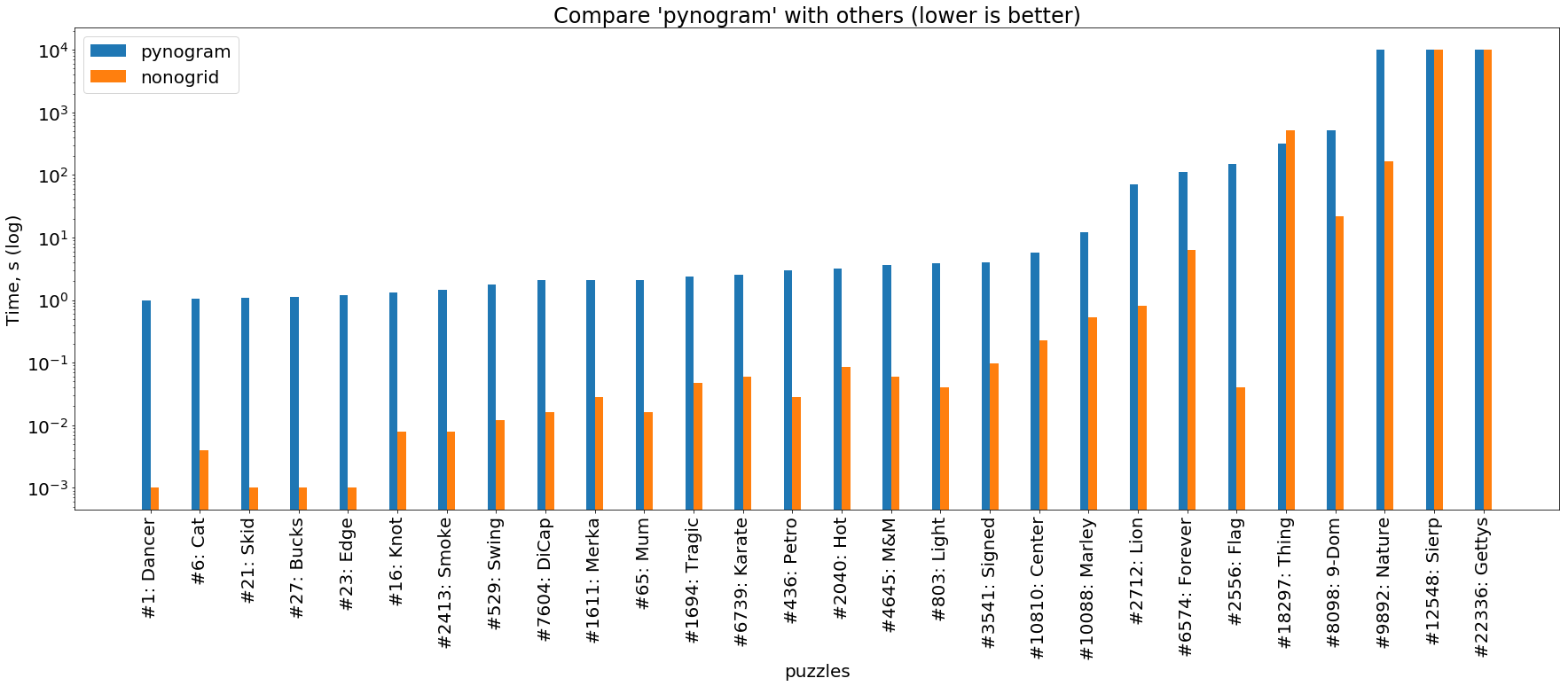
(a imagem é clicável )
E, finalmente, uma comparação dos nossos dois solucionadores descritos aqui. Pode-se ver que o solucionador Rust quase sempre está de 1 a 3 ordens de magnitude à frente do solucionador python.
O + solver pode resolver todos os quebra-cabeças dos sites https://webpbn.com (exceto blotted - com tamanhos de blocos parcialmente ocultos), http://nonograms.org e seu próprio formato (baseado em TOML)
+ resolve nonogramas em preto e branco e em cores com qualquer número de cores
+ pode renderizar quebra-cabeças no console (cor c webpbn.com desenha cores reais)
+ funciona rápido (em comparação com as implementações descritas na comparação de artigos dos solucionadores, consulte a tabela).
- o backtracking permaneceu ineficaz, como na solução Python: alguns quebra-cabeças (por exemplo , um 20x20 tão inofensivo ) podem ser resolvidos por horas (quando a árvore de decisão é muito grande). Talvez, em vez de voltar atrás, valha a pena usar os solucionadores SAT já mencionados no hub É verdade que o único solucionador de SAT que encontrei no Rust à primeira vista parece inacabado e abandonado.
Webassembly
Portanto, reescrever o código no Rust valeu a pena: o solucionador se tornou muito mais rápido. No entanto, o Rust nos oferece outro recurso incrivelmente interessante: compilação no WebAssembly e a capacidade de executar seu código diretamente no navegador.
Para implementar esse recurso, existe uma ferramenta especial para o Rust que fornece os ligantes necessários e gera um padrão para você executar sem problemas as funções do Rust no código JS - este wasm-pack (+ wasm-bindgen ). A maior parte do trabalho com ele e outras ferramentas importantes já está descrita no tutorial Rust and WebAssembly . No entanto, há alguns pontos que eu tive que descobrir por conta própria:
ao ler, cria a sensação de que o tutorial foi escrito principalmente para um desenvolvedor de JS que deseja acelerar seu código com o Rust. Bem, ou pelo menos para alguém familiarizado com o npm . Para mim, como uma pessoa distante do front-end, foi surpreendente descobrir que mesmo o exemplo padrão do livro não deseja trabalhar com um servidor da Web de terceiros diferente do npm run start .
Felizmente, o wasm-pack possui um modo que permite gerar código JS regular (que não é um módulo npm). wasm-pack build --target no-modules --no-typescript na saída produzirá apenas dois arquivos: project-name.wasm - o binário do código Rust compilado no WebAssembly e project-name.js . O último arquivo pode ser incluído em qualquer página HTML <script src="project-name.js"></script> e usar as funções WASM sem se preocupar com npm, webpack, ES6, módulos e outras alegrias do desenvolvedor JS moderno. O modo no-modules é ideal para desenvolvedores não front-end durante o desenvolvimento de um aplicativo WASM, bem como para exemplos e demonstrações, porque não requer nenhuma infraestrutura front-end adicional.
O WebAssembly é bom para tarefas muito pesadas para JavaScript. Antes de tudo, são tarefas que realizam muitos cálculos. E, nesse caso, essa tarefa pode ser executada por um longo tempo, mesmo com o WebAssembly, violando o princípio assíncrono da web moderna. Estou falando de todos os tipos de scripts de aviso: sem resposta que eu observei quando meu solucionador estava funcionando. Para resolver esse problema, você pode usar o mecanismo de trabalho da Web . Nesse caso, o esquema para trabalhar com funções WASM "pesadas" pode ser assim:
- no script principal de um evento (por exemplo, clicando em um botão), envie uma mensagem ao trabalhador com a tarefa de iniciar uma função pesada.
- , .
- - ()
WASM- JS, WASM . - ( ), HashMap , . ( JS) , / .
, Mutex , thread-safe. smart- . thread-safe Rc Arc RefCell RwLock . : 30%. --features=threaded thread-safe , WASM-.
6574 8098 ( 10 ):
, - 40..70% , , (32..37%) thread-safe ( cargo build --release --features=threaded ).
Firefox 67.0 Chromium 74.0.
WASM- ( ). https://webpbn.com/ http://www.nonograms.org/
TODO
"" /, / .
, . "" , , . .
( , 3600 ). WASM , ( , (!) , , WASM). , , - , nonogrid .
. : , , WASM . , ( ) , JS , .
JS. backtrace, .
( TOML- )
Sumário
, (, , etc).
Rust 1-3 PyPy 1.5-2 ( ).
Python Rust , Python (, , comprehensions), Rust-.
Rust WebAssembly . Rust , WASM, ( 1.5 ).
- The 'pbnsolve' Paint-by-Number Puzzle Solver by Jan Wolter and the survey
- The BGU Nonograms Project
- Solving Nonograms by combining relaxations
- An Efficient Approach to Solving Nonograms
- Color and black and white Japanese crosswords on-line
- 'Nonolib' library by Dr. Steven Simpson
- Rust and WebAssembly