Jogue Tetris em AR

Ocorreu-me uma pequena idéia estranha de que a casa poderia ser uma boa plataforma para interpretar Tetris. Não muito longe de mim, havia apenas um edifício adequado para isso. O resultado pode ser visto no vídeo:


O projeto é implementado em um nível bastante baixo, sem o uso de qualquer solução pronta.

Código fonte

Na maioria das vezes, eles usam 2 opções para implementar a realidade aumentada:

• sem marcador, isto é, a posição da câmera é determinada pelo movimento dos pontos principais do seu fluxo de vídeo;
• imagem como um marcador em relação à qual está a posição da câmera.

Essas implementações não requerem preparação especial ou condições especiais.

Há outra opção de implementação - reconhecer um objeto específico e usá-lo como marcador. Isso requer pelo menos sua presença, mas possibilita o controle visual. Um dos métodos desse reconhecimento é a detecção de um objeto por arestas. Tem limitações - o objeto marcador deve ter arestas claramente definidas, ou seja, o objeto provavelmente deve ser sólido.

Ou as bordas devem ser claramente delineadas, como a iluminação deste edifício:



Pode-se ver que a luz de fundo pode ser facilmente separada na imagem e usada para detecção.

Implementação

Em Qt. Essa estrutura permite que você trabalhe em plataformas diferentes e ao mesmo tempo em C ++. Como o desempenho é importante para nós, os profissionais parecem ser uma escolha óbvia.

Embora o Qt não tenha funcionado muito bem com o Android (lançamento longo, a depuração foi desativada), tudo isso foi nivelado pela capacidade de depurar o algoritmo na área de trabalho.

Gráficos tridimensionais foram visualizados no OpenGL bruto incorporado no Qt.

O trabalho com a câmera foi realizado através do Qt. Um vídeo foi gravado para depuração e foi conveniente o suficiente para substituir o fluxo de vídeo da câmera por um fluxo de vídeo de um arquivo.

A saída foi realizada por meio de ferramentas qml. Fazer amigos qml e OpenGL não foi sem problemas, mas não vamos nos alongar nisso.

Para o processamento de imagens, a biblioteca OpenCV está conectada.

Algoritmo de rastreamento

Agora vamos para a parte mais interessante - o algoritmo para rastrear um objeto ao longo de suas bordas.
E comece destacando as bordas da imagem. Todas as arestas do nosso caso têm a forma de linhas retas; portanto, o primeiro pensamento que vem à mente é usar um detector de linha. As transformações de Hough podem ser usadas como um detector de linha. No entanto, esse caminho não me parece muito verdadeiro, já que a transformação Hough é bastante cara e, além disso, esse detector não é muito confiável (isso é subjetivo, talvez tudo dependa da tarefa).
Em vez disso, vamos de uma maneira diferente e mais geral. Não levaremos em conta que nossas linhas são retas, mas trabalharemos simplesmente em uma imagem binária. A presença de arestas será codificada na imagem binária. I.e. um pixel com valor zero significa que existe uma aresta neste local; o valor do pixel é maior que zero - não há aresta. Essa imagem pode ser obtida usando um detector de limites Canny ou uma simples transformação de limite . Esses algoritmos podem ser encontrados no OpenCV.

O OpenCV também tem outra função útil para nós agora - distanceTransform , que pega uma imagem binária na entrada e fornece uma imagem na saída, em pixels, nos quais a distância até o pixel zero mais próximo é codificada.

Agora, suponha que já tenhamos a primeira boa aproximação de onde nosso modelo deve estar localizado. A seguir, descrevemos a função de erro, que descreve até que ponto as bordas da nossa aproximação não coincidem com as bordas da imagem resultante. Usando a imagem de distanceTransform, já somos capazes de fazer isso. E então rodamos o algoritmo de otimização de função, alterando apenas nossa aproximação da posição do objeto no espaço. Como resultado, nossa aproximação deve descrever com precisão a posição real do objeto.
Como resultado, o algoritmo pode ser dividido em dois estágios:

1. Pré-processamento de imagem - binarização, filtragem e uso da função distanceTransfrom.
2. Rastreamento - otimização da função de erro.

Pré-processamento de imagem

Neste ponto, você precisa destacar as bordas da imagem. Você pode usar o detector de limite Canny, mas, no nosso caso, a conversão de limite usual ou sua versão adaptativa funciona melhor (no OpenCV, essas são funções de limite ou adaptiveThreshold). É claro que haverá ruído em tal imagem, portanto é necessário filtrar. Vamos fazer o seguinte: selecione o contorno usando a função OpenCV findCountours e exclua segmentos muito pequenos ou insuficientes como uma linha.

O resultado do processamento pode ser visto na imagem:



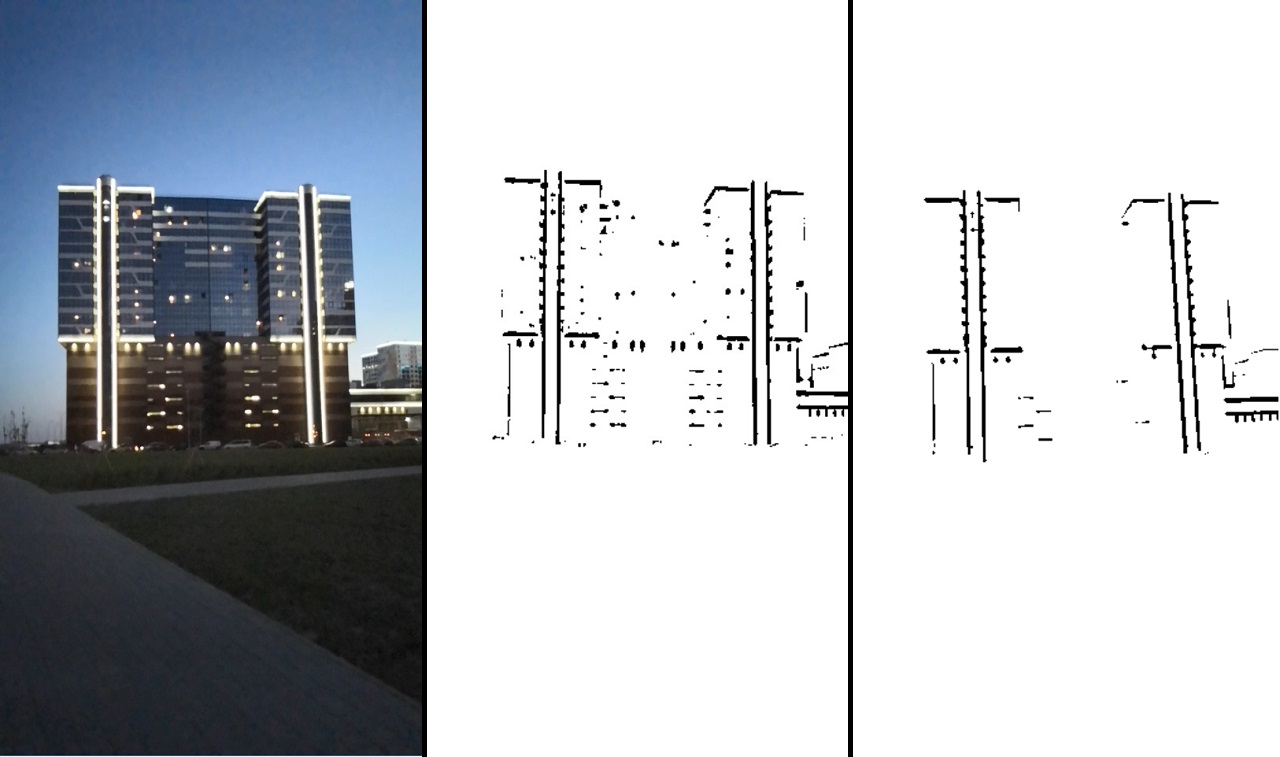
Consistentemente: a imagem original -> após a transformação do limite -> após a filtragem.

Essa imagem já nos diz claramente onde há a borda direita e onde não. Depois disso, usamos a função distanceTransform e, como resultado, teremos informações sobre a distância de cada ponto da borda. A imagem resultante é denotada como .

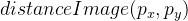
É assim que parece se normalizado e visualizado:



Em seguida, precisaremos de algumas ferramentas matemáticas.

Algoritmo de Otimização de Função

A otimização de funções é a tarefa de encontrar o mínimo de uma função.

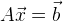
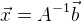
Se estamos lidando com um sistema linear de equações, encontrar um mínimo é bastante simples. Imagine o sistema de equações em forma de matriz: , então nossa solução: . Se temos um sistema de equações sobredeterminado, podemos usar o método dos mínimos quadrados : .

Se nossa função é não linear, a tarefa se torna mais complicada. Para encontrar o mínimo, você pode usar o algoritmo de Gauss-Newton . O algoritmo funciona da seguinte maneira:

1. Supõe-se que já tenhamos uma aproximação inicial da solução que iremos refinar iterativamente.
2. Usando a expansão de Taylor, podemos aproximar nossa função não linear linear no ponto de aproximação atual. Resolvemos o sistema linear de equações resultante pelo método dos mínimos quadrados, obtendo 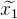. Como resultado, a solução resultante não será uma solução, mas estará mais próxima do que a aproximação atual.
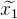3. Substitua a aproximação atual decisão recebida e vá para o passo 2. Repita até que a diferença entre e não será menor que um determinado valor.

Vamos analisar o algoritmo em mais detalhes.

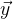
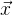
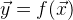
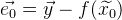
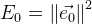
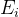
Vamos - função de trabalho, - um vetor anteriormente conhecido de valores de função. Com a solução perfeita para a equação a seguinte declaração é verdadeira . Mas nós temos apenas a sua aproximação . Em seguida, o vetor de erro dessa aproximação é indicado como: . Um erro geral da função será: . Agora encontrando tal em que atingir um mínimo, teremos uma melhor aproximação da solução .
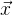
A partir da abordagem iremos aproximar iterativamente, obtendo cada iteração . Para fazer isso, precisamos de cada iteração para calcular a matriz de Jacobi para a função para a aproximação atual, consistindo em derivadas de nossa função:

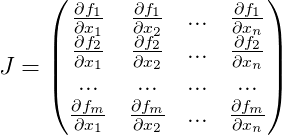
E a seguinte aproximação é dada como: .
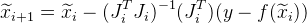
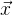
Muitas vezes, as tarefas são construídas de forma que tenhamos um grande número de dados independentes uns dos outros (apenas dos valores ) Como resultado, a matriz geral de Jacobi é muito esparsa. Existe uma maneira de otimizar os cálculos.
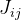
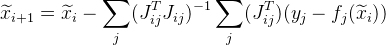
Suponha que uma função comum seja calculada a partir de um conjunto de pontos. A partir do jésimo ponto, obtemos . Em vez de calcular a matriz Jacobi para toda a função, calculamos a matriz de Jacobi especificamente para e denote-o como: . Em seguida, será apresentada a seguinte aproximação: . Além disso, essa alteração permite paralelizar os cálculos.
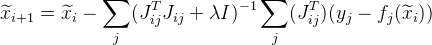
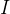
Pode acontecer que o seguinte valor vai dar um erro maior do que . Para resolver esse problema, você pode usar uma modificação do algoritmo - o algoritmo Levenberg-Marquardt . Agregar valor em nossa fórmula: onde É uma matriz unitária. Valor selecionado da seguinte forma:

• primeiro, possui um valor bastante pequeno (tal que o algoritmo converge);
• então, se um erro para mais que , aumente o valor e tente calcular o erro para novamente.

Quanto mais não linear a função quanto maior o valor deve ser . No entanto, quanto maior o valor , mais devagar o algoritmo converge.

Concluímos o algoritmo quando diferente de pequeno o suficiente e leve como uma solução.

O algoritmo é bastante universal e pode ser usado para uma variedade de tarefas.

Modelo de rastreamento matemático

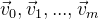
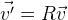
Como estamos lidando com coordenadas no espaço, fica claro que precisamos ser capazes de manipular essas coordenadas. Suponha que tenhamos um conjunto de pontos . E precisamos rotacioná-los em torno do ponto com coordenadas zero. Provavelmente, a maneira mais fácil seria usar a matriz de rotação R , que descreve a rotação necessária: . Se precisarmos mudar os pontos, basta adicionar o vetor desejado t : .
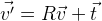
Assim, você pode alterar arbitrariamente a posição de um objeto no espaço. Acontece que as coordenadas do objeto são determinadas pela matriz tridimensional R e pelo vetor tridimensional t , isto é, 12 parâmetros. Além disso, esses parâmetros não são independentes, os componentes da matriz de rotação são interconectados por determinadas condições. Portanto, do ponto de vista do uso dessas funções na otimização, esses parâmetros não são a melhor solução. Existem mais parâmetros do que graus de liberdade, existe uma relação entre eles. Existe outra forma de rotação - a fórmula de rotação de Rodrigue . Essa rotação é especificada por três parâmetros, formando um vetor tridimensional.

O vetor normalizado é o eixo de rotação e o comprimento desse vetor é o ângulo de rotação em torno desse eixo.

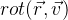
Definimos a função de rotação do vetor v : usando os parâmetros r da fórmula Rodrigue. Nós obtemos a seguinte fórmula a partir disso: .
E no final, podemos definir as coordenadas da posição do objeto com um vetor 6-dimensional:
Temos a seguinte fórmula: .

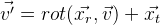
Modelo de câmera pinhole

Agora, descrevemos um modelo matemático simples da câmera usada no projeto:

$$

$$\ vec {p} = \ begin {pmatrix} p_x & p_y \ end {pmatrix} ^ T = cam (\ vec {v}) = \ begin {pmatrix} f_x \ frac {v_x} {v_z} + c_x & f_y \ frac {v_y} {v_z} + c_y \ end {pmatrix} ^ T$$

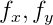
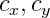
onde - distância focal em pixels; - O centro óptico também está em pixels. Estes são parâmetros individuais da câmera, chamados de parâmetros intrínsecos da câmera. Normalmente, esses parâmetros são conhecidos antecipadamente. Neste projeto, esses parâmetros são selecionados a olho nu.

Este modelo não leva em consideração a distorção da lente das câmeras ( distorção ). Suponha que eles não sejam.

Com este modelo, obtemos uma projeção central, cujos pontos tendem mais para o centro óptico, mais afastados da câmera em que estão. Assim, obtemos o efeito de uma via férrea estreita:



No espaço, a câmera está alinhada com o eixo z , o plano da imagem é paralelo ao plano xy . Complementamos nosso modelo com a capacidade de se mover no espaço:

$$

$$\ vec {p} _j = cam (rot (\ vec {x} _r, \ vec {v} _j) + \ vec {x} _t)$$

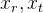
Assim, obtivemos um modelo com o qual podemos, de forma algébrica, simular a projeção de pontos do mundo exterior na imagem da câmera (das coordenadas do mundo para a tela). Para nós, os parâmetros da posição relativa da câmera no espaço permanecem desconhecidos neste modelo. . Esses parâmetros são chamados de parâmetros extrínsecos da câmera.

Rastreamento

Implementado já sem ferramentas OpenCV. Primeiro, precisamos obter a função de erro para a nossa solução aproximada, que foi descrita acima. E escreveremos seu cálculo em etapas:

1. Selecionamos essas arestas do modelo de rastreamento que são visíveis com base nos parâmetros da aproximação atual.
2. Transformamos o conjunto de arestas selecionado em um conjunto fixo de pontos, para simplificar os cálculos. É possível, por exemplo, pegar o enésimo número de pontos de cada aresta ou (uma opção mais correta) escolher essa quantidade para que haja uma distância fixa em pixels entre os pontos. Nós os chamaremos de pontos de controle (no projeto: controlPoint - pontos de controle e controlPixelDistance - a mesma distância fixa em pixels).
3. Projetamos pontos de controle na imagem. Graças ao distanceImage, podemos obter a distância da projeção do ponto de controle até a borda da imagem. No caso ideal, todos os pontos de controle devem estar estritamente nas bordas da imagem, ou seja, a distância da costela deve ser zero. Com base nisso, obtemos um erro para um ponto de controle específico: .
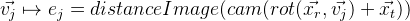4. Temos a seguinte função de erro:

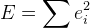
Agora resta encontrar um mínimo de E. Para fazer isso, usamos o algoritmo de Levenberg-Marquardt descrito acima. Como já sabemos, o algoritmo requer o cálculo da matriz de Jacobi, ou seja, funções derivadas. Você pode usar a descoberta numérica de derivadas. Você também pode usar algumas soluções prontas para esse algoritmo. No entanto, neste projeto, tudo foi escrito manualmente, então descreverei a conclusão completa de toda a solução.

Para cada ponto de controle, obtemos uma equação independente de outros pontos. Já foi descrito acima que, neste caso, é possível considerar essas equações independentemente uma da outra, calculando a matriz de Jacobi especificamente para cada uma. Vamos analisá-lo em ordem, usando as regras de diferenciação de uma função complexa:



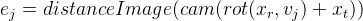
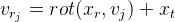
Nós denotamos então



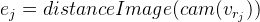
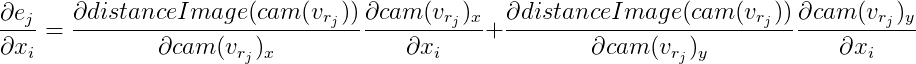
A partir daqui:



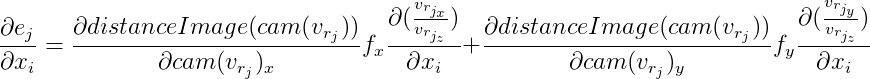
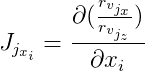
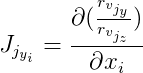
Além disso, denotamos e então:


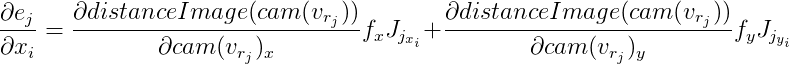
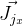
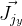
As derivadas de distanceImage são numericamente. E para vetores de computação e você precisará encontrar derivados de acordo com a fórmula de rotação de Rodrigue. Eu encontrei jacobiano por esta fórmula na publicação “Uma fórmula compacta para a derivada de uma rotação 3D em
coordenadas exponenciais »Guillermo Gallego, Anthony Yezzi :

,
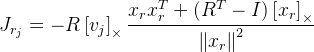
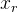
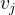
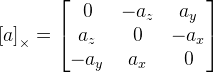
onde R é a matriz de rotação obtida pela fórmula de Rodrigue a partir do vetor de rotação ; - o ponto que estamos mudando; Eu é a matriz de identidade; . Como vemos aqui, temos uma divisão pelo comprimento do vetor de rotação e, se o vetor for zero, a fórmula não funcionará mais. Provavelmente, isso se deve ao fato de que no vetor zero o eixo de rotação não está definido. Se o vetor de rotação estiver muito próximo de zero, usaremos esta fórmula: .
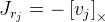
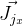
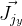
Resta pintar e (aqui o índice j é omitido):


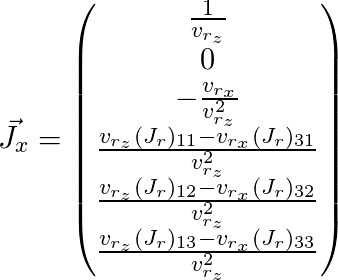
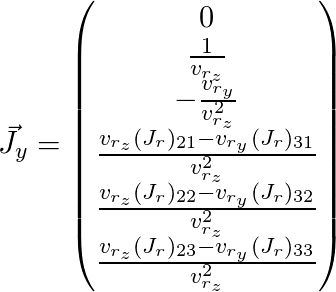
Assim, obtivemos a matriz de Jacobi para o ponto que precisamos e podemos usá-la para o algoritmo de otimização descrito acima.

Existem vários problemas com esse algoritmo. Em primeiro lugar, precisão. Como resultado, a posição global da câmera salta levemente de um quadro para outro. Você pode consertar um pouco. Temos informações a priori de que a posição da câmera não pode mudar drasticamente de quadro para quadro. E podemos reduzir esse tremor adicionando equações adicionais à função.

Deve-se lembrar que o vetor de deslocamento t não é, no nosso caso, a coordenada da posição global da câmera. A posição global é um ponto local com coordenadas zero, portanto, pode ser derivado da seguinte maneira:



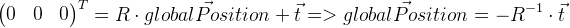
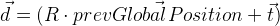
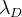
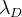
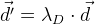
Lembramos a posição do quadro anterior em prevGlobalPosition . Agora, a posição anterior deve estar próxima de zero, ou seja, comprimento do vetor deve ser pequeno o suficiente. I.e. além de outros valores de discrepâncias, o vetor d também deve ser minimizado. Para determinar o grau de influência dessa modificação, introduzimos o valor e multiplique o vetor d adicionando por : . I.e. no algoritmo de otimização, minimizamos adicionalmente o vetor d ' . Obviamente, para isso, será necessário calcular a matriz de Jacobi para ela, que é deduzida da mesma maneira que já a deduzimos acima para a função de erro geral.

O segundo problema do algoritmo é que ele pode ficar preso em mínimos locais. Em outros trabalhos, esse problema é resolvido usando um filtro de partículas. No nosso caso, essa opção acabou sendo, em princípio, suficiente.

Bônus por rastrear um objeto

Conhecendo a posição e a forma do objeto, você pode manipulá-los visualmente, o que tentei demonstrar no vídeo. O objeto foi distorcido usando shaders OpenGL. Com a ajuda do nosso modelo, projetei o ponto do objeto na imagem e, assim, recebi a cor desse ponto. Então você pode mover esse ponto, obtendo efeitos interessantes - por exemplo, transformando-os. No entanto, é preciso lembrar que, mudando de assunto, é necessário que algo permaneça em seu lugar, caso contrário as inconsistências se tornarão visíveis. Além disso, dependendo da qualidade de nosso rastreamento e da forma do objeto, receberemos vários efeitos indesejáveis ​​devido a erros acumulados, que ainda serão. Só precisa ser levado em consideração de alguma forma. No vídeo apresentado acima, eu queria mostrar que a realidade aumentada pode ser usada um pouco mais do que apenas impor objetos virtuais à imagem.

A propósito, o Vuforia SDK implementa o rastreamento de um objeto por sua forma, embora eu não pense que seria possível implementar este projeto com ele, pois não é possível usar arestas estritamente definidas e não pode ser associado à iluminação do edifício.