Um artigo da equipe do Stitch Fix sugere o uso de uma abordagem de pesquisa clínica de estudos de não inferioridade nos testes de marketing e A / B do produto. Essa abordagem é realmente aplicável quando testamos uma nova solução que possui vantagens que não são mensuráveis por testes.
O exemplo mais simples é a perda óssea. Por exemplo, automatizamos o processo de atribuição da primeira lição, mas não queremos diminuir muito a conversão. Ou testamos as alterações focadas em um segmento de usuários, enquanto asseguramos que as conversões em outros segmentos não diminuam muito (ao testar várias hipóteses, não se esqueça das correções).
Escolher a borda direita de não menos eficiência adiciona dificuldades adicionais no estágio de design do teste. A questão de como escolher Δ no artigo não está bem divulgada. Parece que essa escolha não é completamente transparente em ensaios clínicos.
Uma revisão de publicações médicas sobre não inferioridade relata que em apenas metade das publicações a escolha da fronteira é justificada e, muitas vezes, essas justificativas são ambíguas ou não detalhadas.
De qualquer forma, essa abordagem parece interessante, porque Ao reduzir o tamanho da amostra necessário, ele pode aumentar a velocidade dos testes e, portanto, a velocidade da tomada de decisões. -
Daria Mukhina, analista de produto do aplicativo móvel Skyeng.A equipe do Stitch Fix adora testar coisas diferentes. Toda a comunidade tecnológica, em princípio, gosta de realizar testes. Qual versão do site atrai mais usuários - A ou B? A versão A do modelo de recomendação gera mais dinheiro que a versão B? Quase sempre, para testar hipóteses, usamos a abordagem mais simples de um curso básico de estatística:
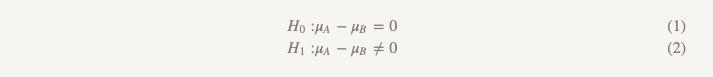
Embora raramente usemos o termo, essa forma de teste é chamada de "teste de hipótese de superioridade". Com essa abordagem, assumimos que não há diferença entre as duas opções. Aderimos a essa idéia e a recusamos apenas se os dados obtidos forem convincentes o suficiente para isso - ou seja, eles demonstram que uma das opções (A ou B) é melhor que a outra.
Testar a hipótese de superioridade é adequado para resolver muitos problemas. Nós liberamos a versão B do modelo de recomendação apenas se obviamente for melhor que a versão A. já usada. Mas, em alguns casos, essa abordagem não funciona tão bem. Vejamos alguns exemplos.
1) Utilizamos um serviço de terceiros que ajuda a identificar cartões bancários falsos. Encontramos outro serviço que custa significativamente menos. Se um serviço mais barato funcionar tão bem quanto o que usamos agora, nós o escolheremos. Não precisa ser melhor que o serviço usado.
2) Queremos abandonar a fonte de dados A e substituí-la pela fonte de dados B. Poderíamos atrasar o abandono de A se B produzir resultados muito ruins, mas não é possível continuar usando A.
3) Gostaríamos de passar da abordagem para a modelagem A para a abordagem B não porque esperamos melhores resultados de B, mas porque isso nos proporciona uma grande flexibilidade operacional. Não temos motivos para acreditar que B será pior, mas não começaremos a transição se for esse o caso.
4) Fizemos várias alterações qualitativas no design do site (versão B) e acreditamos que esta versão é superior à versão A. Não esperamos alterações na conversão ou em quaisquer indicadores-chave de desempenho pelos quais geralmente avaliamos o site. Mas acreditamos que existem vantagens em parâmetros que são incomensuráveis ou que nossas tecnologias não são suficientes para medir.
Em todos esses casos, pesquisar a excelência não é a melhor solução. Mas a maioria dos especialistas nessas situações o usa por padrão. Realizamos cuidadosamente um experimento para determinar corretamente a magnitude do efeito. Se fosse verdade que as versões A e B funcionam de maneira muito semelhante, há uma chance de que não possamos rejeitar a hipótese nula. Concluímos que A e B geralmente funcionam da mesma maneira? Não! A incapacidade de rejeitar a hipótese nula e a adoção da hipótese nula não são a mesma coisa.
Os cálculos do tamanho da amostra (que você, obviamente, executou) geralmente são realizados com limites mais rígidos para o erro de primeiro tipo (probabilidade de rejeição errônea da hipótese nula, freqüentemente chamada de alfa), do que para o erro de segundo tipo (probabilidade de falha na rejeição da hipótese nula, quando supondo que a hipótese nula esteja errada, geralmente chamada beta). O valor típico para alfa é 0,05, enquanto o valor típico para beta é 0,20, o que corresponde a um poder estatístico de 0,80. Isso significa que não podemos detectar a verdadeira influência do valor que indicamos em nossos cálculos de potência com uma probabilidade de 20%, e essa é uma lacuna de informações bastante séria. Como exemplo, vamos considerar as seguintes hipóteses:
H0: minha mochila NÃO está no meu quarto (3)
H1: minha mochila está no meu quarto (4)Se eu procurei no meu quarto e encontrei minha mochila - tudo bem, posso recusar a hipótese nula. Mas se eu olhasse ao redor da sala e não conseguisse encontrar minha mochila (Figura 1), que conclusão devo tirar? Tenho certeza que ele não está lá? Já pesquisei bastante o suficiente? E se eu pesquisasse apenas 80% da sala? Concluir que a mochila definitivamente não está na sala será uma decisão precipitada. Não é de surpreender que não possamos "aceitar a hipótese nula".
A área que procuramos
Não encontramos uma mochila - devemos aceitar a hipótese nula?Figura 1. Pesquisando 80% da sala é o mesmo que conduzir um estudo com capacidade de 80%. Se você não encontrou uma mochila, tendo examinado 80% da sala, é possível concluir que ela não está lá?Então, o que um especialista em dados faz nessa situação? Você pode aumentar bastante o poder de pesquisa, mas precisará de uma amostra muito maior e o resultado ainda será insatisfatório.
Felizmente, esses problemas há muito são estudados no mundo da pesquisa clínica. A droga B é mais barata que a droga A; é esperado que a droga B cause menos efeitos colaterais que a droga A; o medicamento B é mais fácil de transportar porque não precisa ser armazenado na geladeira e o medicamento A é necessário. Testamos a hipótese de não menos eficiência. Isso é necessário para mostrar que a versão B é tão boa quanto a versão A - pelo menos dentro de um certo limite predeterminado de “não menos eficiência”, Δ. Um pouco mais tarde, falaremos mais sobre como definir esse limite. Mas agora suponha que essa seja a menor diferença que seja praticamente significativa (no contexto de ensaios clínicos, isso geralmente é chamado de relevância clínica).
Hipóteses de não menos eficiência transformam tudo de cabeça para baixo:
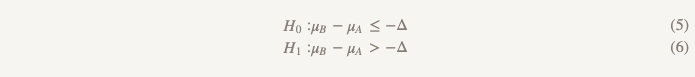
Agora, em vez de assumir que não há diferença, assumimos que a versão B é pior que a versão A, e seguiremos essa suposição até demonstrar que não é. Este é exatamente o momento em que faz sentido usar o teste de uma hipótese unilateral! Na prática, isso pode ser feito construindo um intervalo de confiança e determinando se o intervalo é realmente maior que Δ (Figura 2).
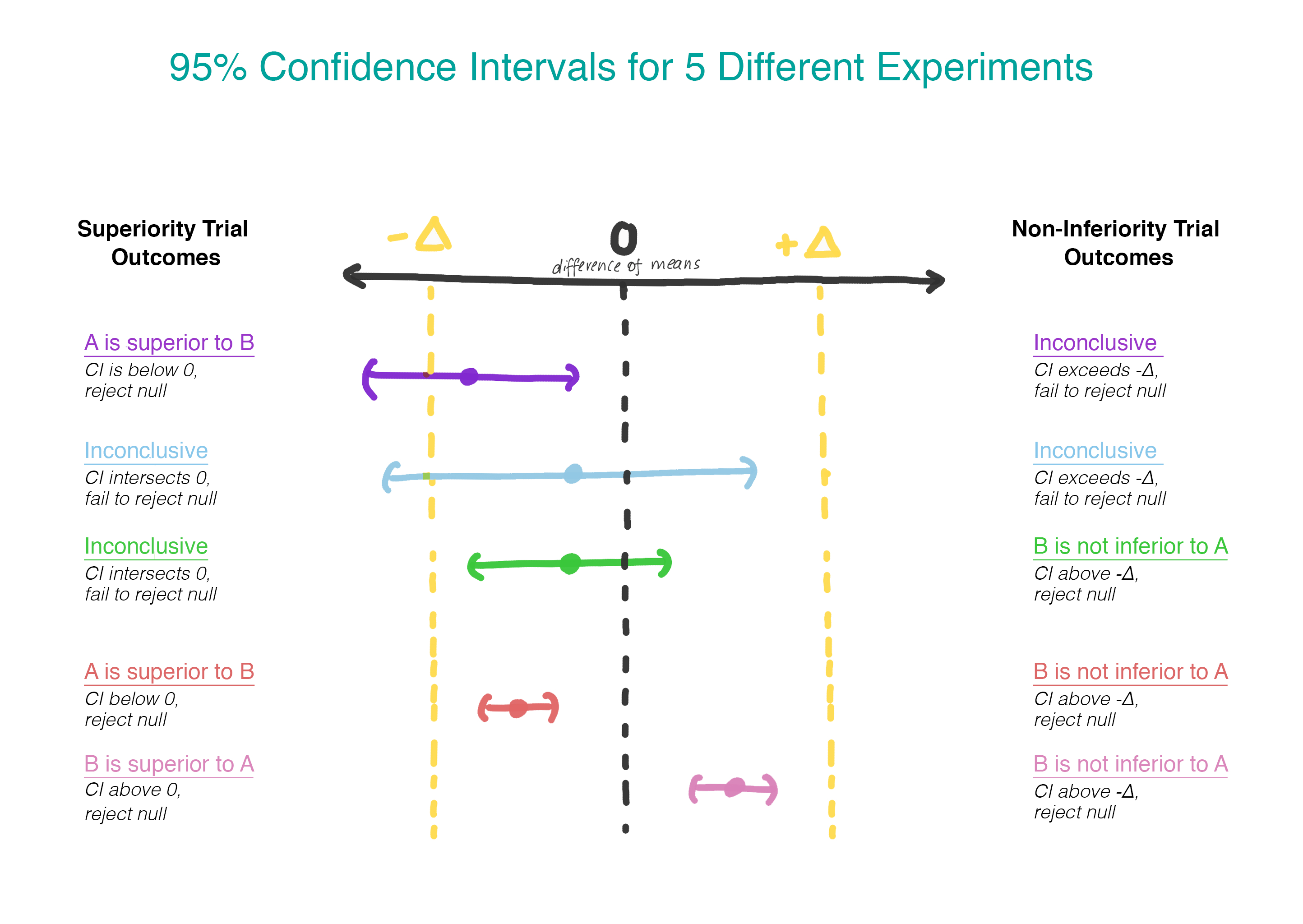
Seleção Δ
Como escolher Δ? O processo de seleção Δ inclui uma justificativa estatística e uma avaliação do sujeito. Existem recomendações normativas no mundo dos ensaios clínicos, das quais se conclui que o delta deve ser a menor diferença clinicamente significativa - uma que será relevante na prática. Aqui está uma citação da liderança européia, com a qual você pode verificar a si mesmo: “Se a diferença foi escolhida corretamente, um intervalo de confiança que se situa completamente entre –∆ e 0 ... ainda é suficiente para demonstrar não menos eficiência. Se esse resultado não parece aceitável, significa que ∆ não foi escolhido adequadamente. ”
Definitivamente, o delta não deve exceder a magnitude do efeito da versão A em relação ao controle verdadeiro (placebo / falta de tratamento), pois isso nos leva a crer que a versão B é pior que o controle verdadeiro e, ao mesmo tempo, demonstra “não menos eficiência”. Suponha que quando a versão A foi introduzida, a versão 0 estivesse em seu lugar ou a função não existisse (veja a Figura 3).
Com base nos resultados do teste da hipótese de superioridade, a magnitude do efeito E foi revelada (isto é, presumivelmente μ ^ A - μ ^ 0 = E). Agora A é o nosso novo padrão e queremos garantir que B não seja inferior a A. Outra maneira de escrever μB - μA≤ - Δ (hipótese nula) é μB≤μA - Δ. Se assumirmos que fazer é igual ou maior que E, então μB ≤ μA - E ≤ placebo. Agora vemos que nossa estimativa para μB excede completamente μA - E, o que refuta completamente a hipótese nula e permite concluir que B não é inferior a A, mas, ao mesmo tempo, μB pode ser ≤ μ placebo, mas isso não é do que precisamos. (figura 3)
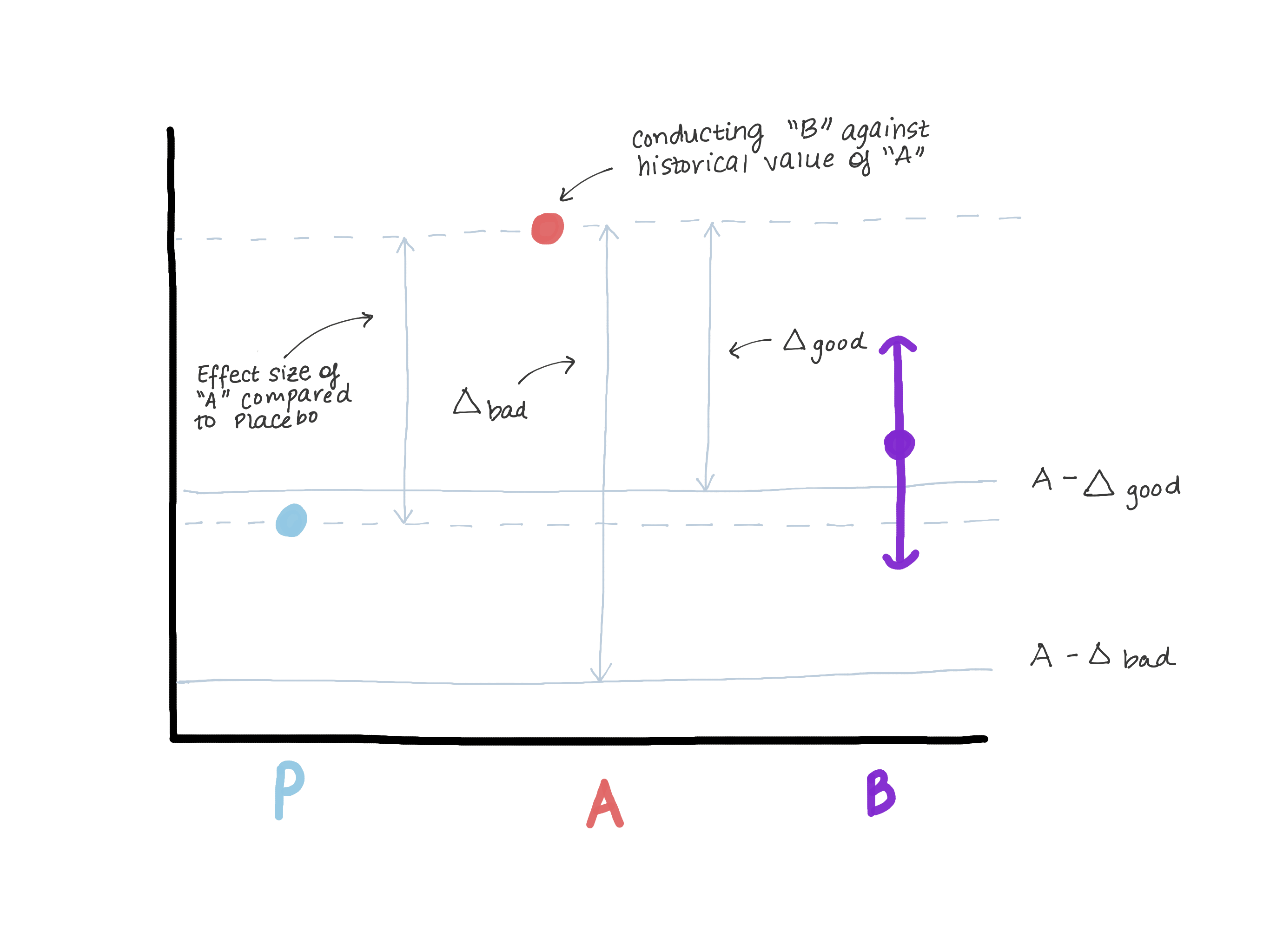Figura 3. Demonstração dos riscos de escolher uma fronteira de não menos eficiência. Se o limite for muito grande, podemos concluir que B não é inferior a A, mas ao mesmo tempo indistinguível do placebo. Não mudaremos o medicamento, que é claramente mais eficaz que o placebo (A), no medicamento que tem a mesma eficácia que o placebo.Escolhendo α
Passamos para a escolha de α. Você pode usar o valor padrão α = 0,05, mas isso não é totalmente honesto. Por exemplo, quando você compra algo na Internet e usa vários códigos de desconto de uma só vez, embora eles não devam ser resumidos, o desenvolvedor apenas cometeu um erro e você se deu bem. De acordo com as regras, o valor de α deve ser igual à metade do valor de α, usado para testar a hipótese de superioridade, ou seja, 0,05 / 2 = 0,025.
Tamanho da amostra
Como estimar o tamanho da amostra? Se você acha que a verdadeira diferença média entre A e B é 0, o cálculo do tamanho da amostra será o mesmo que ao testar a hipótese de superioridade, exceto que você substitui o tamanho do efeito por um limite não menos eficiente, desde que você use
α não menos eficiência = 1/2 superioridade (
α não inferior = 1/2 superior). Se você tem motivos para acreditar que a opção B pode ser um pouco pior que a opção A, mas deseja provar que é pior por não mais que Δ, então você está com sorte! Na verdade, isso reduz o tamanho da sua amostra, porque é mais fácil demonstrar que B é pior que A se você realmente acha que é um pouco pior e não é equivalente.
Exemplo de solução
Suponha que você queira atualizar para a versão B, desde que seja pior que a versão A em não mais que 0,1 pontos em uma escala de satisfação do cliente de 5 pontos ... Abordaremos essa tarefa usando a hipótese de superioridade.
Para testar a hipótese de superioridade, calcularíamos o tamanho da amostra da seguinte maneira:
Ou seja, se você tiver 2103 observações em seu grupo, poderá ter 90% de certeza de que encontrará um efeito de 0,10 ou mais. Mas se o valor de 0,10 for muito alto para você, talvez você não deva testar a hipótese de superioridade. Talvez, para garantir a confiabilidade, você decida realizar um estudo para um tamanho de efeito menor, por exemplo, 0,05. Nesse caso, você precisará de 8407 observações, ou seja, a amostra aumentará quase 4 vezes. Mas e se mantivermos o tamanho da amostra original, mas aumentarmos a potência para 0,99 para não duvidarmos de obter um resultado positivo? Nesse caso, n para um grupo será 3676, o que é melhor, mas aumenta o tamanho da amostra em mais de 50%. E, como resultado, todos nós da mesma forma simplesmente não podemos refutar a hipótese nula e não obtemos a resposta para nossa pergunta.
E se, em vez disso, testamos a hipótese de não menos eficácia?
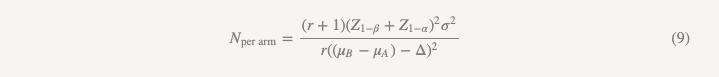
O tamanho da amostra será calculado usando a mesma fórmula, com exceção do denominador.
As diferenças da fórmula usada para testar a hipótese de superioridade são as seguintes:
- Z1 - α / 2 é substituído por Z1 - α, mas se você fizer tudo de acordo com as regras, substitua α = 0,05 por α = 0,025, ou seja, esse é o mesmo número (1,96)
- aparece no denominador (μB - μA)
- θ (magnitude do efeito) é substituído por Δ (limite não menos eficiente)
Se assumirmos que µB = µA, (µB - µA) = 0 e calcular o tamanho da amostra para um limite de eficiência não inferior é exatamente o que obteríamos no cálculo da superioridade para o valor do efeito de 0,1, ótimo! Podemos realizar um estudo da mesma escala com hipóteses diferentes e uma abordagem diferente para conclusões, e obteremos uma resposta para a pergunta que realmente queremos responder.
Agora, suponha que não pensemos realmente que µB = µA e
achamos que µB é um pouco pior, talvez 0,01 unidades. Isso aumenta nosso denominador, reduzindo o tamanho da amostra por grupo para 1737.
O que acontece se a versão B for realmente melhor que a versão A? Refutamos a hipótese nula de que B é pior que A em mais de Δ e aceitamos a hipótese alternativa de que B, se pior, não é pior que Δ e poderia ser melhor. Tente colocar essa conclusão em uma apresentação multifuncional e veja o que vem dela (sério, experimente). Em uma situação em que você precisa se concentrar no futuro, ninguém quer concordar em "piorar por não mais que Δ e, possivelmente, melhor".
Nesse caso, podemos realizar um estudo, chamado muito brevemente "testar a hipótese de que uma das opções é superior à outra ou inferior a ela". Ele usa dois conjuntos de hipóteses:
O primeiro conjunto (o mesmo que ao testar a hipótese de não menos eficiência):
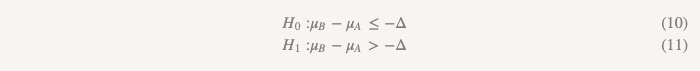
O segundo conjunto (o mesmo que ao testar a hipótese de superioridade):
Testamos a segunda hipótese apenas se a primeira for rejeitada. Nos testes sequenciais, mantemos o nível geral de erros do primeiro tipo (α). Na prática, isso pode ser alcançado criando um intervalo de confiança de 95% para a diferença entre as médias e verificando se o intervalo inteiro excede -Δ. Se o intervalo não exceder -Δ, não podemos rejeitar o valor zero e parar. Se o intervalo inteiro realmente exceder Δ, continuamos e vemos se o intervalo contém 0.
Há outro tipo de pesquisa que não discutimos - estudos de equivalência.
Estudos desse tipo podem ser substituídos por estudos para testar a hipótese de não menos eficácia e vice-versa, mas na verdade eles têm uma diferença importante. Um teste para testar a hipótese de não menos eficiência visa mostrar que a opção B é pelo menos tão boa quanto A. E um estudo de equivalência visa mostrar que a opção B é pelo menos tão boa quanto A, e a opção A é tão boa quanto B, o que é mais complicado. Em essência, estamos tentando determinar se todo o intervalo de confiança está na diferença de médias entre ΔΔ e Δ. Tais estudos requerem um tamanho amostral maior e são menos frequentes. Portanto, na próxima vez em que você realizar um estudo em que sua principal tarefa é garantir que a nova versão não seja pior, não aceite "a incapacidade de refutar a hipótese nula". Se você quiser testar uma hipótese realmente importante., Considere várias opções.