O livro "Machine Learning: Algorithms for Business"

Oi, habrozhiteli! Marcos Lopez de Prado compartilha o que eles costumam esconder - os algoritmos de aprendizado de máquina mais lucrativos que ele usa há duas décadas para gerenciar grandes fundos de fundos dos investidores mais exigentes.

O aprendizado de máquina muda quase todos os aspectos de nossas vidas; os algoritmos MO executam tarefas que, até recentemente, eram confiáveis ​​apenas por especialistas confiáveis. Num futuro próximo, o aprendizado de máquina dominará as finanças, a previsão do futuro será coisa do passado e os investimentos não serão mais sinônimos de jogos de azar.

Aproveite a chance de participar da “revolução da máquina”, para isso basta conhecer o primeiro livro, que fornece uma análise completa e sistemática dos métodos de aprendizado de máquina em relação ao financiamento: começando com estruturas de dados financeiros, marcando a série financeira, marcando a série financeira, ponderando a amostra, diferenciando a série temporal e terminando com toda a parte dedicada ao backtesting correto das estratégias de investimento.

Trecho. Compreendendo estratégias de risco

15.1 Relevância

As estratégias de investimento são frequentemente implementadas em termos de posições mantidas até que uma das duas condições seja atendida: 1) a condição para deixar a posição com lucros (obter lucros) ou 2) a condição para deixar a posição com perdas (interromper a perda). Mesmo quando a estratégia não declara explicitamente uma parada de perda, sempre há um limite implícito de parada de perda no qual o investidor não pode mais financiar sua posição (chamada de margem) ou incorre em danos causados ​​por um aumento na perda não realizada. Como a maioria das estratégias possui (explícita ou implicitamente) essas duas condições de saída, faz sentido modelar a distribuição dos resultados por meio de um processo binomial. Por sua vez, isso nos ajudará a entender quais combinações de taxas de apostas, riscos e pagamentos não são econômicos. O objetivo deste capítulo é ajudá-lo a avaliar quando uma estratégia está vulnerável a pequenas mudanças em qualquer uma dessas quantidades.

Considere uma estratégia que produz n apostas mutuamente independentes e distribuídas de forma idêntica por ano, em que o resultado Xi da aposta i ∈ [1, n] é o lucro π> 0 com probabilidade P [Xi = π] = p e a perda –π com probabilidade P [Xi = –Π] = 1 - p. Você pode imaginar p como a precisão de um classificador binário, no qual um resultado afirmativo significa apostar na oportunidade e um resultado negativo significa oportunidade perdida: declarações verdadeiras são recompensadas, declarações falsas são punidas e resultados negativos (verdadeiros ou falsos) não têm recompensas. Como os resultados das apostas {Xi} i = 1, ..., n são independentes, calcularemos os momentos esperados por aposta. O lucro esperado de uma aposta é E [Xi] = πp + (–π) (1 - p) = π (2p - 1). 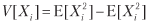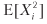A variação é onde = π2p + (–π) 2 (1 - p) = π2, portanto, V [Xi] = π2 - π2 (2p - 1) 2 = π2 [1– (2p - 1) 2] = 4π2p (1 - p ) Para n taxas idênticas e distribuídas de forma idêntica por ano, a taxa média anual de Sharpe (θ) é


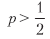
Observe como π equilibra a equação acima porque os pagamentos são simétricos. Como no caso gaussiano, θ [p, n] pode ser entendido como um valor t redimensionado1. Isso ilustra o fato de que mesmo para pequenas a razão Sharpe pode ser elevada para um n suficientemente grande. Isso serve como base econômica para o comércio de alta frequência, em que p pode ser um pouco maior que 0,5 e a chave para uma atividade cambial bem-sucedida é o aumento de n. A razão Sharpe é uma função da precisão, e não da correção, porque perder uma oportunidade (declaração negativa) não é recompensada ou punida diretamente (embora muitas declarações negativas possam levar a n pequeno, o que reduzirá o coeficiente de Sharpe a zero).

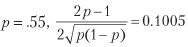
Por exemplo, para e para atingir uma taxa média anual de Sharpe de 2, 396 apostas por ano são necessárias. A Listagem 15.1 verifica esse resultado experimentalmente. A Figura 15.1 mostra a razão Sharpe como uma função da precisão para diferentes frequências de aposta.

Listagem 15.1. Sharpe ratio em função do número de apostas

out,p=[],.55 for i in xrange(1000000): rnd=np.random.binomial(n=1,p=p) x=(1 if rnd==1 else -1) out.append(x) print np.mean(out),np.std(out),np.mean(out)/np.std(out) 

Essa equação expressa claramente a troca entre precisão (p) e frequência (n) para um dado coeficiente de Sharpe (θ). Por exemplo, para fornecer uma taxa Sharpe anual média de 2 para uma estratégia que produz apenas taxas semanais (n = 52), será necessária uma precisão razoavelmente alta p = 0,6336.

15.3 Pagamentos assimétricos

Considere uma estratégia que produz n taxas identificadas e mutuamente independentes por ano, em que o resultado Xi da aposta i ∈ [1, n] é π + com probabilidade P [Xi = π +] = p, e o resultado π– (π– <π + ) acontece com probabilidade P [Xi = π_] = 1 - p. O lucro esperado de uma aposta é E [Xi] = pπ + + (1 - p) π– = (π + - π–) p + π–. A dispersão é V [Xi] =, onde



Finalmente, podemos resolver a equação anterior para 0 ≤ p ≤ 1 e obter


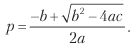
onde:
a = (n + θ2) (π + - π–) 2;
b = [2nπ - θ2 (π + - π -)] (π + - π–);


Nota: A Listagem 15.2 verifica essas operações simbólicas usando o shell do Python SymPy Live em execução no serviço de nuvem do Google App Engine: live.sympy.org .

Listagem 15.2. Usando a biblioteca SymPy para operações simbólicas

 >>> from sympy import * >>> init_printing(use_unicode=False,wrap_line=False,no_global=True) >>> p,u,d=symbols('pu d') >>> m2=p*u**2+(1-p)*d**2 >>> m1=p*u+(1-p)*d >>> v=m2-m1**2 >>> factor(v) 

A equação acima responde à seguinte pergunta: para uma dada regra de negociação caracterizada pelos parâmetros {π–, π +, n}, qual é o grau de precisão p necessário para atingir a razão Sharpe igual a θ *? Por exemplo, para obter θ = 2 para n = 260, π– = –1,01, π + = 0,005, precisamos de p = 0,72. Devido ao grande número de apostas, uma mudança muito pequena em p (de p = 0,7 a p = 0,72) promoveu a proporção de Sharpe de θ = 1,173 a θ = 2. Por outro lado, isso também nos diz que essa estratégia é vulnerável a pequenas apostas. mudanças na p. A Listagem 15.3 implementa a derivação da precisão esperada. Na fig. 15.2 mostra a suposta precisão em função de n e π–, onde π + = 0,1 e θ * = 1,5. À medida que o limite π– se torna mais negativo para um dado n, é necessário um grau mais alto p para atingir θ * para um determinado limite π +. À medida que o número n se torna menor para um determinado limite π–, é necessário um grau mais alto de p para atingir θ * para um dado π +.

Listagem 15.3. Cálculo da precisão estimada

 def binHR(sl,pt,freq,tSR): ´´´ 

Para uma determinada regra de negociação caracterizada pelos parâmetros {sl, pt, freq}, qual é a precisão mínima necessária para atingir a taxa de Sharpe igual a tSR?

1) Entradas
sl: limiar de parada de perda
pt: limite de lucro
freq: o número de apostas por ano
TSR: rácio médio anual alvo de Sharpe
2) Sair
p: precisão mínima p necessária para atingir a RST
´´´
a = (freq + tSR ** 2) * (pt-sl) ** 2
b = (2 * freq * sl-tSR ** 2 * (pt-sl)) * (pt-sl)
c = frequência * sl ** 2
p = (- b + (b ** 2-4 * a * c) **. 5) / (2. * a)
retornar p


A Listagem 15.4 resolve θ [p, n, π–, π +] para a frequência estimada de apostas n. Na fig. 15.3 mostra a frequência estimada dependendo de p e π–, onde π + = 0,1 e θ * = 1,5. À medida que o limite π– se torna mais negativo para um determinado grau p, é necessário um número n maior para atingir θ * para um determinado limite π +. À medida que o grau p se torna menor para um determinado limite π–, é necessário um número n maior para atingir θ * para um determinado limite π +.

Listagem 15.4. Cálculo da frequência estimada de apostas

 def binFreq(sl,pt,p,tSR): ´´´ 

Para uma dada regra de negociação, caracterizada pelos parâmetros {sl, pt, freq}, quantas apostas por ano são necessárias para atingir o coeficiente Sharp tSR com um grau de precisão p?

Nota: equação com radicais, verifique se há soluções estranhas.

1) Entradas
sl: limiar de parada de perda
pt: limite de lucro
p: grau de precisão p
TSR: rácio médio anual alvo de Sharpe
2) Sair
freq: o número de apostas necessárias por ano
´´´
freq = (tSR * (pt-sl)) ** 2 * p * (1-p) / ((pt-sl) * p + sl) ** 2 # possivelmente estranho
caso contrário, np.isclose (binSR (sl, pt, freq, p), tSR): return
retorno freq



»Mais informações sobre o livro podem ser encontradas no site do editor
» Conteúdo
» Trecho

Cupom de desconto de 25% para vendedores ambulantes - Machine Learning

Após o pagamento da versão em papel do livro, uma versão eletrônica do livro é enviada por e-mail.