Introdução às redes neurais convolucionais

O curso completo em russo pode ser encontrado neste link .
O curso de inglês original está disponível neste link .


Novas palestras são agendadas a cada 2-3 dias.

Entrevista com Sebastian

- Então, estamos novamente com Sebastian na terceira parte deste curso. Sebastian, eu sei que você fez muito desenvolvimento usando redes neurais convolucionais. Você pode nos contar um pouco mais sobre essas redes e quais são elas? Estou certo de que os alunos do nosso curso ouvirão com menos interesse, porque nesta parte eles terão que desenvolver a rede neural convolucional.
Ótimo! Assim, as redes neurais convolucionais são uma excelente maneira de estruturar a rede, construindo a chamada invariância (alocação de recursos imutáveis). Por exemplo, considere a idéia de reconhecimento de padrões no palco ou na fotografia, você quer entender se Sebastian está ou não representado. Não importa em que parte da fotografia eu estou, onde minha cabeça está localizada - no centro da fotografia ou no canto. Reconhecimento da minha cabeça, meu rosto deve ocorrer independentemente de onde eles estão localizados na imagem. Isso é invariância, variabilidade de localização, que é realizada por redes neurais convolucionais.
Muito interessante! Você pode nos dizer as principais tarefas nas quais as redes neurais convolucionais são usadas?
- As redes neurais convolucionais são bastante usadas quando se trabalha com áudio e vídeo, incluindo imagens médicas. Eles também são usados ​​em tecnologias de linguagem, onde especialistas usam aprendizado profundo para entender e reproduzir construções de linguagem. De fato, existem muitas aplicações para essa tecnologia, eu diria mesmo que são infinitas! Sua tecnologia pode ser usada em finanças e em outras áreas.
"Eu usei redes neurais convolucionais para analisar imagens de satélite."
Ótimo! A tarefa padrão!
- Em sua opinião, podemos considerar as redes neurais convolucionais como a última e mais avançada ferramenta no desenvolvimento da aprendizagem profunda?
Ha! Eu já aprendi a nunca dizer nunca. Sempre haverá algo novo e incrível!
"Então ainda temos trabalho a fazer?" :)
- Haverá trabalho suficiente!
Excelente! Neste curso, estamos apenas ensinando futuros pioneiros em aprendizado de máquina. Você deseja seus alunos antes que eles comecem a construir sua primeira rede neural convolucional?
- Aqui está um fato interessante para você. As redes neurais convolucionais foram inventadas em 1989, e isso faz muito tempo! A maioria de vocês nem nasceu naquela época, o que significa que não é o gênio do algoritmo que importa, mas os dados nos quais esse algoritmo opera. Vivemos em um mundo onde existem muitos dados para analisar e procurar padrões. Temos a capacidade de emular as funções da mente humana usando essa enorme quantidade de dados. Quando você trabalha em redes neurais convolucionais, tente se concentrar em encontrar os dados corretos e aplicá-los - veja o que acontece e, às vezes, pode ser uma verdadeira mágica, como foi o caso em nosso caso quando estávamos resolvendo o problema de detectar o câncer de pele.
Ótimo! Bem, vamos finalmente à mágica!

1. Introdução

Na última lição, aprendemos como desenvolver redes neurais profundas capazes de classificar imagens de elementos de vestuário a partir do conjunto de dados Fashion MNIST.



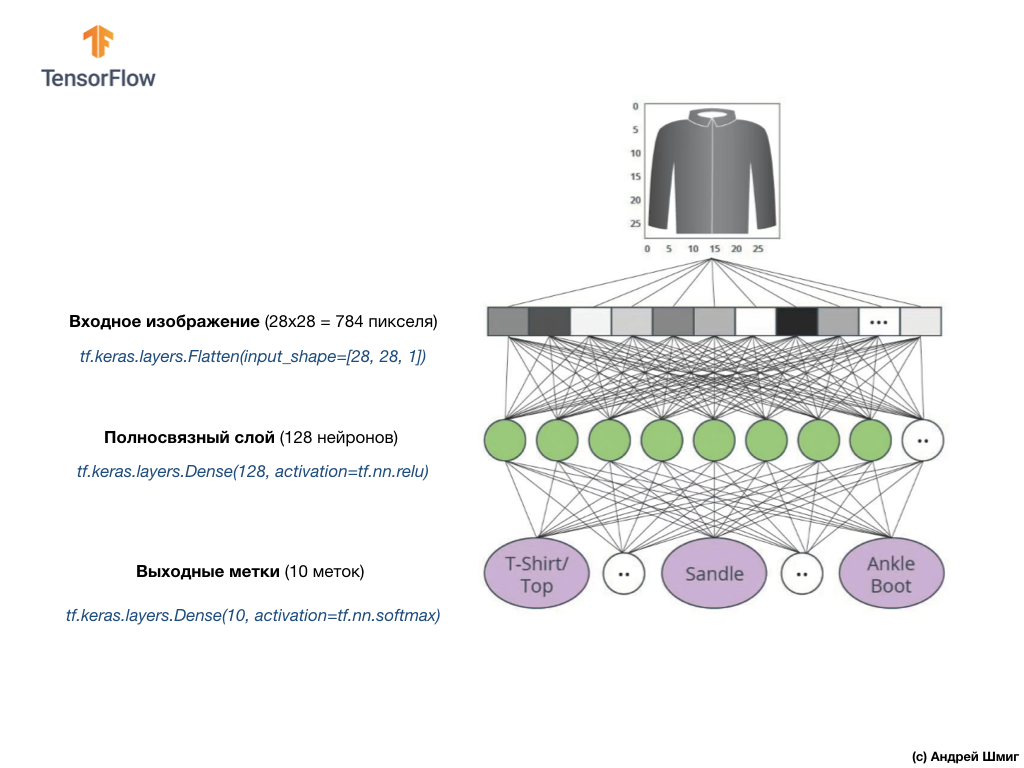
Os resultados obtidos durante o trabalho na rede neural foram impressionantes - 88% de precisão na classificação. E isso está em algumas linhas de código (sem levar em conta o código para a construção de gráficos e imagens)!

model = tf.keras.Sequential([ tf.keras.layers.Flatten(input_shape=(28, 28, 1)), tf.keras.layers.Dense(128, activation=tf.nn.relu), tf.keras.layers.Dense(10, activation=tf.nn.softmax) ]) 

 model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy']) 

 NUM_EXAMPLES = 60000 train_dataset = train_dataset.repeat().shuffle(NUM_EXAMPLES).batch(32) test_dataset = test_dataset.batch(32) 

 model.fit(train_dataset, epochs=5, steps_per_epoch=math.ceil(num_train_examples/32)) 

 test_loss, test_accuracy = model.evaluate(test_dataset, steps=math.ceil(num_test_examples/32)) print(': ', test_accuracy) 

: 0.8782

Também experimentamos o efeito do número de neurônios em camadas ocultas e o número de iterações de treinamento na precisão do modelo. Mas como tornamos esse modelo ainda melhor e mais preciso? Uma maneira de conseguir isso é usar redes neurais convolucionais, abreviada para SNA. O SNA mostra maior precisão na resolução dos problemas de classificação de imagens do que as redes neurais padrão totalmente conectadas que encontramos nas classes anteriores. É por esse motivo que o SNA se tornou tão popular e foi graças a eles que se tornou possível uma inovação tecnológica no campo da visão de máquina.

Nesta lição, aprenderemos como é fácil desenvolver um classificador SNA do zero usando o TensorFlow e o Keras. Usaremos o mesmo conjunto de dados do Fashion MNIST que usamos na lição anterior. No final desta lição, comparamos a precisão da classificação dos elementos de vestuário da rede neural anterior com a rede neural convolucional desta lição.

Antes de mergulhar no desenvolvimento, vale a pena aprofundar um pouco o princípio de funcionamento das redes neurais convolucionais.

Dois conceitos básicos em redes neurais convolucionais:

• convolução
• operação de subamostragem (pooling, max pooling)

Vamos dar uma olhada neles.

Convolução

Nesta parte da lição, aprenderemos uma técnica chamada convolução. Vamos ver como isso funciona.

Tire uma imagem em tons de cinza e, por exemplo, imagine que suas dimensões são 6 px de altura e 6 px de largura.



Nosso computador interpreta a imagem como uma matriz bidimensional de pixels. Como nossa imagem está em tons de cinza, o valor de cada pixel estará no intervalo de 0 a 255. 0 - preto, 255 - branco.

Na imagem abaixo, vemos uma representação da imagem 6px x 6px e os valores de pixel correspondentes:



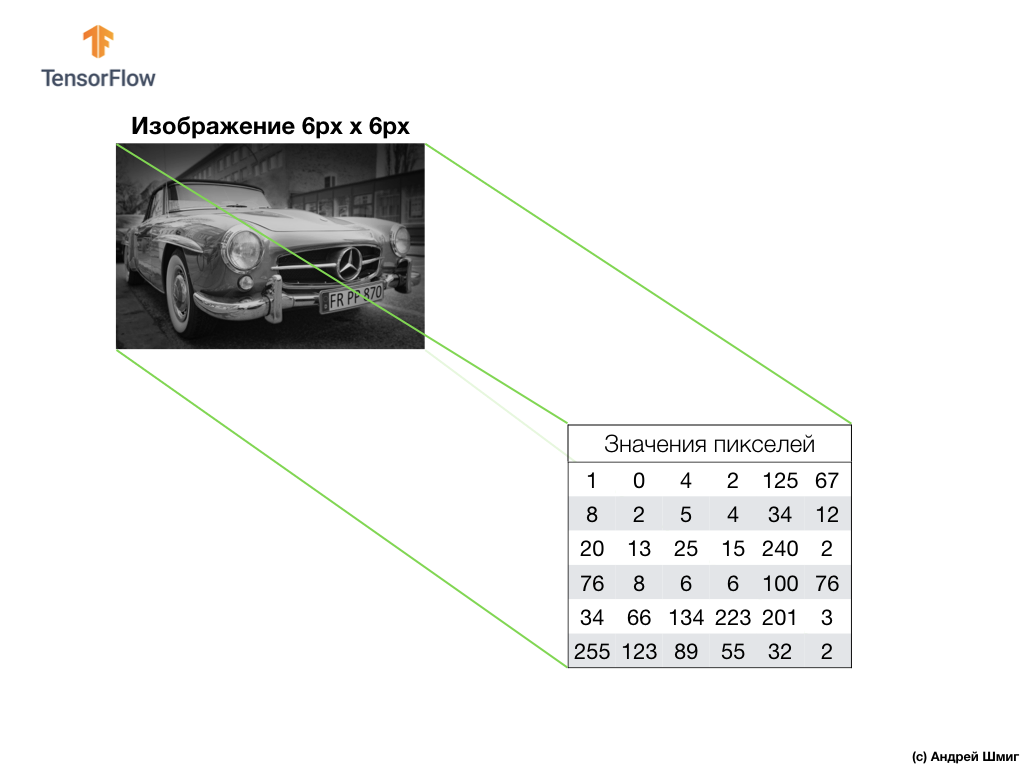
Como você já sabe, antes de trabalhar com imagens, é necessário normalizar os valores de pixel - traga os valores para um intervalo de 0 a 1. No entanto, neste exemplo, para facilitar a explicação, salvaremos os valores de pixel da imagem e não os normalizaremos.

A essência da convolução é criar outro conjunto de valores, chamado de kernel ou filtro. Um exemplo pode ser visto na imagem abaixo - uma matriz 3 x 3:



Então podemos digitalizar nossa imagem usando o kernel. As dimensões da nossa imagem são 6x6px e os núcleos são 3x3px. A camada convolucional é aplicada ao núcleo e a cada seção da imagem de entrada.

Vamos imaginar que queremos convolver sobre um pixel com um valor de 25 (3 linhas, 3 colunas) e a primeira coisa que precisa ser feita é centralizar o núcleo sobre esse pixel:



Na imagem, o posicionamento do núcleo é destacado em amarelo. Agora, examinaremos apenas os valores de pixel que estão em nosso retângulo amarelo, cujos tamanhos correspondem aos tamanhos do nosso núcleo de convolução.

Agora pegamos os valores de pixel da imagem e do kernel, multiplicamos cada pixel da imagem pelo pixel correspondente do kernel e adicionamos todos os valores do produto e atribuímos o valor de pixel resultante à nova imagem.







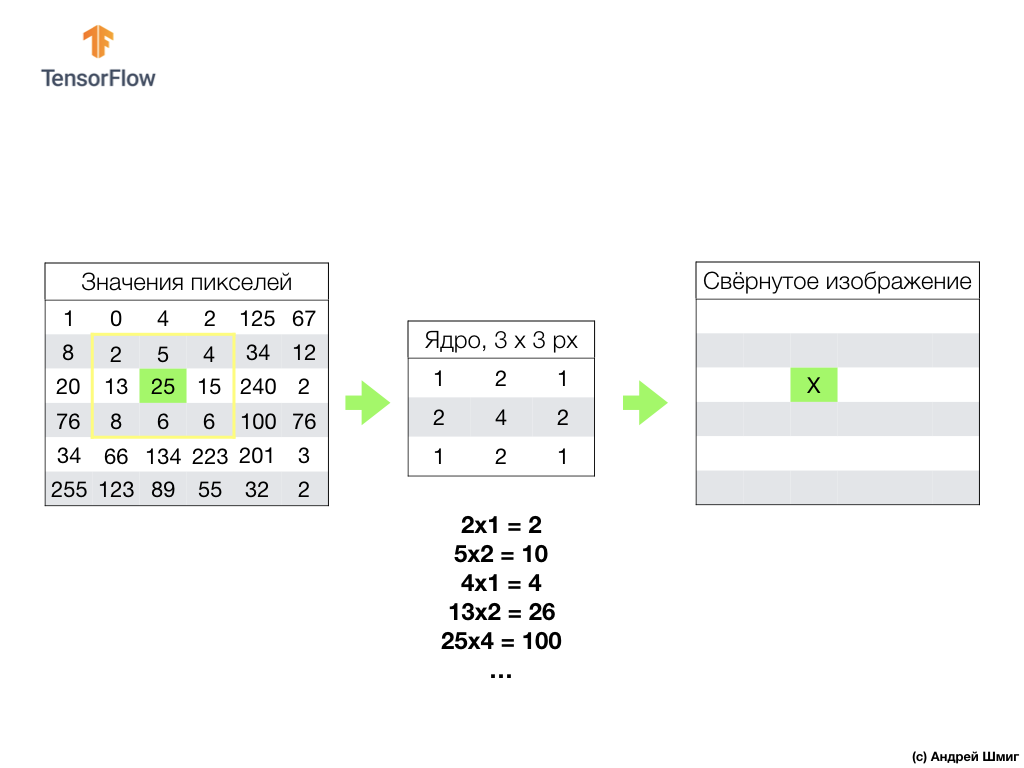
Realizamos uma operação semelhante com todos os pixels em nossa imagem. Mas o que deveria acontecer com os pixels nas bordas?



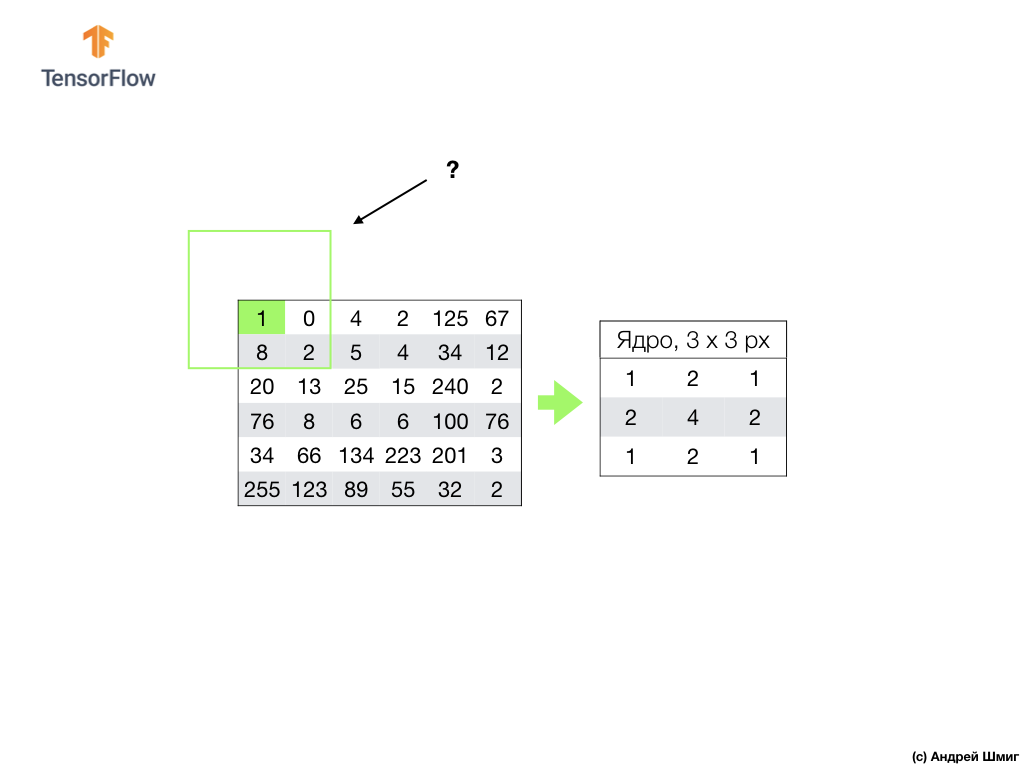
Existem várias soluções. Primeiramente, podemos simplesmente ignorar esses pixels, mas, neste caso, perderemos informações sobre a imagem, que podem ser significativas, e a imagem minimizada se tornará menor que a original. Em segundo lugar, podemos simplesmente "matar", com zero valor, os pixels cujos valores principais estão além do escopo da imagem. O processo é chamado alinhamento.



Agora que fizemos o alinhamento com valores de zero pixel, podemos calcular o valor do pixel final na imagem minimizada como antes.

Uma convolução é o processo de aplicação de um núcleo (filtro) a cada parte da imagem de entrada; por analogia com uma camada totalmente conectada (camada densa), veremos que a convolução é a mesma camada em Keras.

Agora, vejamos o segundo conceito de redes neurais convolucionais - a operação de subamostragem (pooling, max-pooling).

Operação de subamostragem (pool, max-pooling)

Agora, consideraremos o segundo conceito fundamental subjacente às redes neurais convolucionais - a operação de subamostragem (pooling, max-pooling). Em palavras simples, uma operação de subamostragem é o processo de compactar (reduzir o tamanho) de uma imagem adicionando os valores dos blocos de pixels. Vamos ver como isso funciona em um exemplo concreto.



Para executar a operação de subamostragem, precisamos decidir sobre dois componentes desse processo - o tamanho da amostra (o tamanho da grade retangular) e o tamanho da etapa. Neste exemplo, usaremos uma grade retangular 3x3 e a etapa 3. A etapa determina o número de pixels pelos quais a grade retangular deve ser deslocada ao executar a operação de subamostragem.

Depois de decidirmos o tamanho da grade e o tamanho da etapa, precisamos encontrar o valor máximo de pixel que cai na grade selecionada. No exemplo acima, os valores 1, 0, 4, 8, 2, 5, 20, 13, 25 caem na grade.O valor máximo é 25. Esse valor é "transferido" para a nova imagem. A grade é deslocada 3 pixels para a direita e o processo de seleção do valor máximo e transferência para uma nova imagem é repetido.



Como resultado, uma imagem menor será obtida em comparação com a imagem de entrada original. No nosso exemplo, foi obtida uma imagem com metade do tamanho da imagem original. O tamanho da imagem final varia dependendo da escolha do tamanho da grade retangular e do tamanho da etapa.

Vamos ver como isso funcionará no Python!

Sumário

Familiarizamos-nos com conceitos como convolução e operação de pool máximo.

Convolução é o processo de aplicação de um filtro ("núcleo") em uma imagem. A operação de subamostragem por valor máximo é o processo de redução do tamanho de uma imagem combinando um grupo de pixels em um único valor máximo desse grupo.

Como veremos na parte prática, a camada convolucional pode ser adicionada à rede neural usando a camada Conv2D em Keras. Essa camada é semelhante à camada Densa e contém pesos e compensações que passam por otimização (seleção). Conv2D camada Conv2D também contém filtros ("kernels"), cujos valores também são otimizados. Portanto, na camada Conv2D , os valores dentro da matriz de filtro são as variáveis ​​que sofrem otimização.

Alguns termos que conseguimos encontrar:

• SNS - redes neurais convolucionais. Uma rede neural que contém pelo menos uma camada convolucional. Um SNA típico contém outras camadas, como camadas de amostra e totalmente conectadas.
• Convolução é o processo de aplicação de um filtro ("núcleo") em uma imagem.
• Um filtro (núcleo) é uma matriz de tamanho menor que os dados de entrada, destinada à conversão de dados de entrada em blocos.
• Alinhamento é o processo de adicionar, na maioria das vezes zero valores, às bordas de uma imagem.
• A operação de subamostragem é o processo de redução do tamanho de uma imagem através da amostragem. Existem vários tipos de camadas de subamostragem, por exemplo, uma camada de subamostragem média (amostragem de um valor médio); no entanto, uma subamostragem pelo valor máximo é mais frequentemente usada.
• A subamostragem pelo valor máximo é o processo de subamostragem, durante o qual muitos valores são convertidos em um único valor - o máximo entre a amostragem.
• Etapa - o número de pixels de deslocamento pelo filtro (núcleo) na imagem.
• Amostragem (downsampling) - o processo de redução do tamanho da imagem.

CoLab: classificação de elementos de vestuário Fashion MNIST usando uma rede neural convolucional

Estávamos circulados em torno de um dedo! Faz sentido executar essa parte prática somente após a conclusão da parte anterior - todo o código, exceto um bloco, permanece o mesmo. A estrutura de nossa rede neural está mudando, e essas são quatro linhas adicionais para camadas neurais convolucionais e camadas de subamostragem no valor máximo (pool máximo).

 model = tf.keras.Sequential([ tf.keras.layers.Conv2D(32, (3,3), padding='same', activation=tf.nn.relu, input_shape=(28, 28, 1)), tf.keras.layers.MaxPooling2D((2, 2), strides=2), tf.keras.layers.Conv2D(64, (3,3), padding='same', activation=tf.nn.relu), tf.keras.layers.MaxPooling2D((2, 2), strides=2), tf.keras.layers.Flatten(), tf.keras.layers.Dense(128, activation=tf.nn.relu), tf.keras.layers.Dense(10, activation=tf.nn.softmax) ]) 

Todas as explicações detalhadas de como trabalhar, elas prometem nos dar na próxima parte - 4 partes.

Ah sim. A precisão do modelo na fase de treinamento tornou-se igual a 97% (o modelo “treinado” nas epochs=10 ) e, ao executar o conjunto de dados para os testes, mostrou exatamente 91%. Um aumento notável na precisão em relação à arquitetura anterior, onde usamos apenas camadas totalmente conectadas - 88%.

Sumário

Nesta parte da lição, estudamos um novo tipo de rede neural - rede neural convolucional. Nós nos familiarizamos com termos como “convolução” e “operação de pool máximo”, desenvolvemos e treinamos uma rede neural convolucional a partir do zero. Como resultado, vimos que nossa rede neural convolucional produz mais precisão do que a rede neural que desenvolvemos na última lição.

Nota do autor da tradução.

O curso é chamado "Introdução à aprendizagem profunda usando o TensorFlow", portanto, não vamos reclamar da falta de explicações detalhadas do princípio das redes neurais convolucionais (camadas) - os próximos dois artigos serão sobre o princípio de operação da rede neural convolucional e sua estrutura interna (os artigos não estão relacionados ao curso, mas foram recomendados pelos participantes do StackOverflow para uma melhor compreensão do que está acontecendo).

... e call to action padrão - inscreva-se, coloque um plus e compartilhe :)
YouTube
Telegram
VKontakte