Julia e computação paralela

Desde seu lançamento em agosto de 2018, Julia vem ganhando popularidade ativamente, entrando nos 10 principais idiomas do Github e nas 20 habilidades profissionais mais populares de acordo com a Upwork . Para iniciantes, os cursos começam e os livros são publicados . Julia é usada para planejamento de missões espaciais , farmacometria e modelagem climática .

Antes de prosseguir para a computação distribuída em Julia, passemos à experiência daqueles que já experimentaram a oportunidade de um novo PL para problemas aplicados - desde a equação de difusão em dois núcleos até mapas astronômicos em um supercomputador.

Computação paralela e fatores que afetam o desempenho da computação paralela

A maioria dos computadores modernos possui mais de um processador e vários computadores podem ser combinados em um cluster. Usar o poder de vários processadores permite realizar muitos cálculos mais rapidamente. O desempenho é afetado por dois fatores principais: a velocidade dos próprios processadores e a velocidade do acesso à memória. Em um cluster, esta CPU terá o acesso mais rápido à RAM localizado no mesmo computador ou host. Ainda mais surpreendente, esses problemas são relevantes em um laptop multi-core típico devido a diferenças na velocidade da memória principal e do cache. Portanto, um bom ambiente multiprocessador deve permitir que você controle o uso de parte da memória por um processador específico.

Computação paralela em Julia

Julia possui várias primitivas internas para computação paralela em cada nível: vetorização (SIMD), multithreading e computação distribuída.

O próprio multiencadeamento de Julia permite que o usuário use os recursos de um laptop com vários núcleos, enquanto as primitivas de chamada remota e busca remota permitem distribuir o trabalho entre muitos processos no cluster. Além dessas primitivas internas, vários pacotes no ecossistema Julia fornecem processamento paralelo eficiente.

Vetorização automática em Julia

Os modernos chips Intel fornecem várias extensões de conjunto de comandos. Entre eles estão várias versões da Streaming SIMD Extension (SSE) e várias gerações de extensões de vetores (disponíveis nas famílias de processadores mais recentes). Essas extensões fornecem programação no estilo SIMD (Single Instruction Multiple Data) , fornecendo uma aceleração significativa para o código que se presta a esse estilo de programação. O poderoso compilador Julia da LLia pode gerar automaticamente código de máquina altamente eficiente para funções básicas e definidas pelo usuário em qualquer arquitetura, como o Hardware SIMD (suportado pelo LLVM ), que permite ao usuário se preocupar menos em escrever código especializado para cada uma dessas arquiteturas. Outra vantagem de usar o compilador para melhorar o desempenho, em vez de codificar manualmente "hot loops" em um assembly, é que ele é significativamente melhor para o futuro. Sempre que a arquitetura do conjunto de instruções da próxima geração é lançada, o código personalizado da Julia se torna automaticamente mais rápido.

Multithreading

O multithreading em Julia geralmente assume a forma de loops paralelos. Também existem primitivas para bloqueios e atômicos que permitem aos usuários sincronizar seu código. As primitivas paralelas de Julia são simples, mas poderosas. É mostrado que eles escalam para milhares de nós e processam terabytes de dados .

Computação distribuída

Embora as primitivas internas de Julia sejam suficientes para implantações paralelas em larga escala, há vários pacotes para trabalhos mais especializados. O ClusterManagers.jl fornece interfaces para vários sistemas de enfileiramento de tarefas comumente usados ​​em clusters de computação, como o Sun Grid Engine e o Slurm . DistributedArrays.jl fornece uma interface conveniente para matrizes de dados distribuídas por um cluster. Isso combina os recursos de memória de várias máquinas, o que possibilita o uso de matrizes grandes demais para caber em uma máquina. Cada processo é executado na parte da matriz que possui, fornecendo uma resposta pronta para a pergunta de como o programa deve ser dividido entre as máquinas.

Em alguns aplicativos herdados, os usuários preferem não repensar seu modelo paralelo e desejam continuar usando a simultaneidade no estilo MPI . Para eles, o MPI.jl fornece um invólucro fino em torno do MPI que permite aos usuários usar procedimentos de passagem de mensagens no estilo MPI.

Julia em batalha

O Projeto Celeste é uma colaboração entre Julia Computing, Intel Labs, JuliaLabs @ MIT, Lawrence Berkeley National Labs e a Universidade da Califórnia em Berkeley.

Celeste é um modelo hierárquico totalmente gerador que usa inferência estatística para determinar matematicamente a localização e as características das fontes de luz no céu. Este modelo permite que os astrônomos identifiquem galáxias promissoras para direcionar espectrógrafos e ajuda a entender o papel da energia escura, da matéria escura e da geometria do universo.

Exemplo do Sloan Digital Sky Survey (SDSS)

Usando os recursos de computação paralela de Julia, a equipe de pesquisa da Celeste processou 55 terabytes de dados visuais e classificou 188 milhões de objetos astronômicos em apenas 15 minutos, resultando no primeiro catálogo completo de todos os objetos visíveis do Sloan Digital Sky Survey . Este é um dos maiores problemas de otimização matemática já resolvidos pela humanidade.

O projeto Celeste usou 9.300 nós Knights Landing (KNL) no supercomputador NERSC Cori Phase II para executar 1,3 milhão de threads em 650.000 núcleos KNL, que combinaram a lista de aplicativos com velocidades superiores a 1 petaflops por segundo , tornando Julia a única dinâmica uma linguagem de alto nível que já conseguiu tal feito. ?? Mas a sincronização dos telescópios e o processamento de dados para uma imagem de buraco negro em 10.04.19 quebrou esse recorde? Parece que o Python foi usado principalmente por lá.

Programação paralela com Julia usando MPI

Tradução de material do blog de física de plasma Claudio 2018-09-30

Julia existe desde 2012 e, após mais de seis anos de desenvolvimento, a versão 1.0 foi finalmente lançada. Esta é uma etapa importante que me inspirou a criar um novo post (após vários meses de silêncio). Desta vez, veremos como fazer programação paralela em Julia usando o paradigma da interface de transmissão de mensagens (MPI) através da biblioteca de código aberto Open MPI. Faremos isso resolvendo um problema físico real: difusão de calor através de uma região bidimensional.

Figura 1. Supercomputador Sequoia no LLNL com quase 1,6 milhão de processadores disponíveis para simulação numérica de armas nucleares. hpc.llnl.gov

Esta será uma aplicação MPI bastante avançada, voltada para aqueles que já têm algum entendimento da computação paralela. Por isso, não vou dar um passo a passo, mas focar em aspectos específicos que, na minha opinião, são de interesse (em particular, o uso de células fantasmas e a transmissão de mensagens em uma grade bidimensional). Seguindo a tradição de seus posts recentes, o código discutido aqui será apresentado apenas parcialmente. Isso é acompanhado por uma solução completa que você pode encontrar no Github - Diffusion.jl .

A computação paralela entrou no "mundo comercial" nos últimos anos. Essa é uma solução padrão para aplicativos ETL (Extract-Transform-Load), onde o problema em questão é embaraçosamente paralelo: cada processo é executado independentemente de todos os outros, e nenhuma conexão de rede é necessária (até a etapa final de "redução", onde cada solução local é montada em solução global).

Em muitas aplicações científicas, é necessário transmitir informações através de uma rede de cluster. Esses problemas "paralelos" são frequentemente simulações numéricas: problemas de astrofísica, modelagem climática, biologia, sistemas quânticos etc. Em alguns casos, essas simulações são realizadas em dezenas e até milhões de processadores (Fig. 1), e a memória é distribuída entre diferentes processadores. Normalmente, esses processadores interagem em um supercomputador por meio do paradigma da interface de transmissão de mensagens (MPI).

Qualquer pessoa que trabalhe com computação de alto desempenho deve estar familiarizada com o MPI. Permite o uso da arquitetura de cluster em um nível muito baixo. Teoricamente, um pesquisador pode atribuir a cada CPU sua própria carga de computação. Ele / ela pode decidir exatamente quando e quais informações devem ser transferidas entre os processadores e se isso deve ocorrer de forma síncrona ou assíncrona.

E agora vamos voltar ao conteúdo deste post, onde veremos como escrever uma solução para uma equação de tipo de difusão usando MPI. Já discutimos um esquema explícito para uma equação unidimensional desse tipo ( a propósito, também discutimos isso ). No entanto, neste post, consideraremos uma solução bidimensional.

O código Julia apresentado aqui é essencialmente uma tradução do código C / Fortran , explicado naquele magnífico post de Fabien Durnak.

Neste post, não analisarei em detalhes a velocidade do dimensionamento e o número de processadores. Principalmente porque só tenho dois processadores com os quais posso jogar em casa (processador Intel Core i7 no meu MacBook Pro) ... No entanto, ainda posso dizer com orgulho que o código Julia apresentado nesta postagem, mostra aceleração significativa ao usar dois processadores contra um. Enfim: é mais rápido que os códigos Fortran e C equivalentes! (mais sobre isso mais tarde)

Aqui estão os tópicos que abordaremos neste post:

• Julia: Minhas primeiras impressões
• Como instalar o Open MPI no seu computador
• Problema: propagação através de um domínio bidimensional
• Comunicação entre processadores: a necessidade de células fantasmas
• Usando MPI
• Visualização da solução
• Desempenho
• Conclusões

1. Primeiras impressões de Julia

Na verdade, eu conheci Julia recentemente, então decidi me concentrar em algumas "primeiras impressões" aqui.

A principal razão pela qual me interessei por Julia é que ela promete ser uma estrutura de uso geral com desempenho comparável ao C e Fortran , preservando a flexibilidade e a facilidade de uso de linguagens de script como Matlab ou Python . De fato, Julia deve ser capaz de escrever aplicativos de ciência de dados / computação de alto desempenho que são executados no computador local, na nuvem ou em supercomputadores corporativos.

Um aspecto de que não gosto é o fluxo de trabalho, que parece sub-ideal para quem, como eu, usa IntelliJ e PyCharm diariamente (o plugin IntelliJ Julia é terrível). Eu também experimentei o Juno IDE , que provavelmente é a melhor solução no momento, mas ainda preciso me acostumar.

Um aspecto que demonstra como Julia ainda não atingiu sua “maturidade” é o quão variada e desatualizada é a documentação de muitos pacotes ( para pacotes que foram mantidos à tona, tudo foi descartado desde o ano passado ). Ainda não encontrei uma maneira de escrever uma matriz de números de ponto flutuante no disco em um formato formatado ( agora é fácil encontrá-lo ). Obviamente, você pode gravar em disco cada elemento da matriz em um loop duplo, mas soluções melhores devem estar disponíveis. É difícil encontrar essas informações e a documentação deve ser abrangente.

Outro aspecto que se destaca na primeira vez em que Julia é usada é a escolha de usar a indexação de uma para matrizes. Embora eu ache isso um pouco chato do ponto de vista prático, certamente não quebra o acordo, já que não é exclusivo de Julia (Matlab e Fortran também usam a indexação começando com um).

Agora, para o aspecto bom e mais importante: Julia pode realmente ser muito rápida. Fiquei impressionado ao ver como o código Julia que escrevi para este post pode funcionar melhor do que o código Fortran e C equivalente, mesmo que eu o tenha traduzido para Julia. Dê uma olhada na seção de desempenho, se você estiver interessado.

2. Instalando o Open MPI

MPI aberto é uma biblioteca de interface de sistema de mensagens de código aberto. Outras bibliotecas conhecidas incluem MPICH e MVAPICH. Desenvolvido pela Ohio State University, o MVAPICH é atualmente a biblioteca mais avançada, pois também pode suportar clusters de GPU - o que é especialmente útil para aplicativos de Deep Learning (na verdade, existe uma colaboração estreita entre a NVIDIA e a equipe MVAPICH).

Todas essas bibliotecas são construídas em uma interface comum: API MPI. Portanto, não importa se você usa uma ou outra biblioteca: o código que você escreveu pode permanecer o mesmo.

O projeto MPI.jl no Github é um wrapper para o MPI. Sob o capô, ele usa as instalações C e Fortran MPI. Funciona muito bem, embora não tenha alguns dos recursos disponíveis nesses outros idiomas.

Para executar o MPI na Julia, você precisará instalar o Open MPI separadamente no seu computador. Se você possui um Mac, achei este guia muito útil. É importante observar que você também precisará instalar o gcc (o compilador GNU), pois o Open MPI requer os compiladores Fortran e C. Instalei a versão do Open MPI 3.1.1, que também é confirmada pelo mpiexec --version no meu terminal.

Após a instalação do Open MPI no seu computador, você deve instalar o cmake . Novamente, se você possui um Mac, é tão fácil quanto digitar brew install cmake no seu terminal.

No momento, você está pronto para instalar o pacote MPI na Julia. Abra Julia REPL e digite using Pkg Pkg.add («MPI») . Normalmente, nesse ponto, você poderá importar o pacote usando o MPI para importar. No entanto, eu também tive que criar o pacote através do Pkg.build («MPI») antes de funcionar.

3. Problema: equação de difusão bidimensional

A equação de difusão é um exemplo de uma equação diferencial parcial parabólica. Ele descreve fenômenos como difusão de calor ou difusão de concentração (segunda lei de Fick). Em duas dimensões espaciais, a equação de difusão é escrita

Solução $$$u (x, y, t)$mostra como a temperatura / concentração muda (dependendo de estudarmos a distribuição do calor ou a difusão de substâncias) no espaço e no tempo. De fato, as variáveis xey representam as coordenadas espaciais, e o componente de tempo é representado pela variável t . A quantidade D é o "coeficiente de difusão" e determina com que rapidez, por exemplo, o calor se propagará pela região física. Semelhante ao discutido (em mais detalhes) em um post anterior, a equação acima pode ser discretizada usando o chamado "esquema explícito" da solução. Não vou entrar nos detalhes que você pode encontrar no blog, basta escrever uma solução numérica no seguinte formato:

onde k índices que percorrem a grade espacial, j no tempo. A primeira camada de tempo é preenchida a partir das condições iniciais e cada subseqüente $$$u ^ {j + 1} _ {i, k}$calculado usando os valores da camada anterior. Na figura, os nós vermelhos indicam os nós da camada $$$u ^ {j}$necessários para calcular o valor no ponto $$$u ^ {j + 1} _ {i, k}$

A equação (1) é realmente tudo o que é necessário para encontrar uma solução em toda a área em cada etapa subsequente. É bastante simples implementar código que faz isso sequencialmente com um processo na CPU. No entanto, aqui queremos discutir uma implementação paralela que usa vários processos.

Cada processo será responsável por encontrar uma solução em parte de todo o domínio espacial. Problemas como difusão de calor, que não são candidatos claros à computação distribuída, exigem a troca de informações entre processos. Para esclarecer esse ponto, vejamos a figura

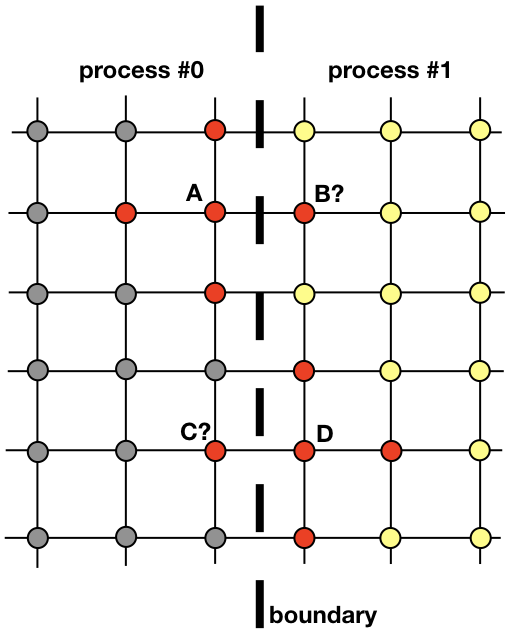
Dois processos vizinhos devem interagir para encontrar uma solução perto da fronteira. O processo 0 deve conhecer o valor da solução em B para calcular a solução no ponto de grade A. Da mesma forma, o processo 1 deve conhecer o valor no ponto C para calcular a solução no ponto de grade D. Esses valores são desconhecidos para os processos até que haja uma conexão entre os processos 0 e 1 .

Ele mostra como os processos 0 e 1 precisarão interagir para avaliar uma solução próxima ao limite. É aqui que o MPI entra em cena. Na próxima seção, veremos uma maneira eficaz de enviar mensagens.

4. Comunicação entre processos: células fantasmas

Um conceito importante na dinâmica dos fluidos computacional é o conceito de células fantasmas. Esse conceito é útil sempre que um domínio espacial é decomposto em vários subdomínios, cada um dos quais resolvido por um único processo.

Para entender o que são células fantasmas, vejamos duas áreas vizinhas na imagem anterior novamente. O processo 0 é responsável por encontrar a solução no lado esquerdo, enquanto o processo 1 encontra-a no lado direito do domínio espacial. No entanto, devido à forma do estêncil (Fig. 2) próximo à borda, os dois processos terão que trocar dados entre si. Aqui está o problema: é muito ineficiente que o processo 0 e o processo 1 se comuniquem cada vez que eles precisam de um nó de um processo vizinho: isso levaria a custos de comunicação inaceitáveis.

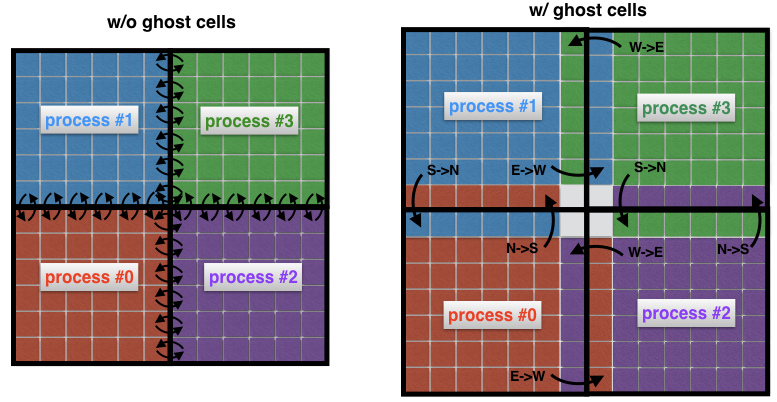
Fig. 4 Conexão entre processos sem (esquerda) e com (direita) células fantasmas. Sem células intermediárias, cada célula na borda de um subdomínio deve transmitir sua própria mensagem para um processo vizinho. O uso de células fantasmas permite minimizar o número de mensagens transmitidas, pois muitas células pertencentes aos limites do processo trocam uma mensagem por vez. Aqui, por exemplo, o processo 0 transfere todo o limite norte para o processo 1 e todo o limite leste para o processo 2.

Em vez disso, é prática comum cercar subdomínios "reais" com células adicionais chamadas células fantasmas, como mostrado na Figura 4 (à direita). Essas células fantasmas são cópias da solução nas bordas dos subdomínios vizinhos. A cada etapa, o limite antigo de cada subdomínio é passado para os vizinhos. Isso permite calcular uma nova solução na borda de um subdomínio com sobrecarga de comunicação significativamente reduzida. O efeito líquido é a aceleração do código.

5. Usando MPI

Existem muitos tutoriais MPI. Aqui, apenas quero descrever os comandos expressos na linguagem shell MPI.jl para Julia que usei para resolver o problema de difusão bidimensional. Esses são alguns comandos básicos usados ​​em quase todas as implementações de MPI.

5.1 Localizando vizinhos do processo

Para nossa tarefa, decomporemos nossa região bidimensional em muitos subdomínios retangulares, como mostra a figura abaixo.

Figura 5. Decomposição cartesiana de uma região bidimensional dividida em 12 subdomínios. Observe que as classificações MPI (identificadores de processo) começam do zero.

Observe que os eixos y são invertidos em relação ao uso normal para associar o eixo x às linhas e o eixo y às colunas da matriz da solução.

Para se comunicar entre diferentes processos, cada processo deve conhecer seus vizinhos. Existe um comando MPI muito útil que faz isso automaticamente e é chamado MPI_Cart_create . Infelizmente, o shell Julia MPI não inclui esse comando avançado (e adicioná-lo não parece trivial); portanto, decidi criar uma função que executa a mesma tarefa. Para torná-lo mais compacto, eu costumava usar o operador ternário . Você pode encontrar esta função abaixo.

 function neighbors(my_id::Int, nproc::Int, nx_domains::Int, ny_domains::Int) id_pos = Array{Int,2}(undef, nx_domains, ny_domains) for id = 0:nproc-1 n_row = (id+1) % nx_domains > 0 ? (id+1) % nx_domains : nx_domains n_col = ceil(Int, (id + 1) / nx_domains) if (id == my_id) global my_row = n_row global my_col = n_col end id_pos[n_row, n_col] = id end neighbor_N = my_row + 1 <= nx_domains ? my_row + 1 : -1 neighbor_S = my_row - 1 > 0 ? my_row - 1 : -1 neighbor_E = my_col + 1 <= ny_domains ? my_col + 1 : -1 neighbor_W = my_col - 1 > 0 ? my_col - 1 : -1 neighbors = Dict{String,Int}() neighbors["N"] = neighbor_N >= 0 ? id_pos[neighbor_N, my_col] : -1 neighbors["S"] = neighbor_S >= 0 ? id_pos[neighbor_S, my_col] : -1 neighbors["E"] = neighbor_E >= 0 ? id_pos[my_row, neighbor_E] : -1 neighbors["W"] = neighbor_W >= 0 ? id_pos[my_row, neighbor_W] : -1 return neighbors end 

Fizemos o mesmo quando construímos labirintos

A entrada para esta função é my_id , que é a classificação (ou identificador) do processo, o número de processos nproc , o número de divisões na direção x nx_domains e o número de divisões na direção y ny_domains .

Vamos verificar esse recurso agora. Por exemplo, olhando novamente para a fig. 5, podemos verificar a saída do processo do ranking 4 e do processo do ranking 11. Vamos entrar no REPL:

 julia> neighbors(4, 12, 3, 4) Dict{String,Int64} with 4 entries: "S" => 3 "W" => 1 "N" => 5 "E" => 7 

e

 julia> neighbors(11, 12, 3, 4) Dict{String,Int64} with 4 entries: "S" => 10 "W" => 8 "N" => -1 "E" => -1 

Como você pode ver, eu uso as direções cardinais "N", "S", "E", "W" para indicar a localização de um vizinho. Por exemplo, o processo 4 tem o processo 3 como um vizinho localizado ao sul de sua posição. Você pode verificar se todos os resultados acima estão corretos, uma vez que "-1" no segundo exemplo significa que nenhum vizinho foi encontrado nos lados "norte" e "leste" do processo 11.

5.2 Mensagens

Como vimos anteriormente, a cada iteração, cada processo envia suas bordas para os processos vizinhos. Ao mesmo tempo, cada processo recebe dados de seus vizinhos. Esses dados são armazenados por cada processo na forma de "células fantasmas" e são usados ​​para calcular a solução próxima ao limite de cada subdomínio.

A MPI possui um comando MPI_Sendrecv muito útil que permite enviar e receber mensagens simultaneamente entre dois processos. Infelizmente, o MPI.jl não fornece essa funcionalidade, mas ainda é possível obter o mesmo resultado usando as MPI_Receive e MPI_Receive separadamente.

Aqui está o que foi feito na próxima função updateBound! , que atualiza as células fantasmas a cada iteração. A entrada para esta função é uma solução 2D global u, que inclui células fantasmas, bem como todas as informações relacionadas a um processo específico que executa uma função (qual é sua classificação, quais são as coordenadas de seu subdomínio, quais são seus vizinhos). A função primeiro envia suas bordas para os vizinhos e depois recebe suas bordas. A parte receptora está sendo finalizada através da equipe MPI.Waitall! , que garante que todas as mensagens esperadas foram recebidas antes de atualizar as células laterais para um subdomínio específico de interesse.

 function updateBound!(u::Array{Float64,2}, size_total_x, size_total_y, neighbors, comm, me, xs, ys, xe, ye, xcell, ycell, nproc) mep1 = me + 1 #assume, to start with, that this process is not going to receive anything rreq = Dict{String, MPI.Request}( "N" => MPI.REQUEST_NULL, "S" => MPI.REQUEST_NULL, "E" => MPI.REQUEST_NULL, "W" => MPI.REQUEST_NULL ) recv = Dict{String, Array{Float64,1}}() ghost_boundaries = Dict{String, Any}( "N" => (xe[mep1]+1, ys[mep1]:ye[mep1]), "S" => (xs[mep1]-1, ys[mep1]:ye[mep1]), "E" => (xs[mep1]:xe[mep1], ye[mep1]+1), "W" => (xs[mep1]:xe[mep1], ys[mep1]-1) ) is_receiving = Dict{String, Bool}("N" => false, "S" => false, "E" => false, "W" => false) #send neighbors["N"] >=0 && MPI.Isend(u[xe[mep1], ys[mep1]:ye[mep1]], neighbors["N"], me + 40, comm) neighbors["S"] >=0 && MPI.Isend(u[xs[mep1], ys[mep1]:ye[mep1]], neighbors["S"], me + 50, comm) neighbors["E"] >=0 && MPI.Isend(u[xs[mep1]:xe[mep1], ye[mep1]], neighbors["E"], me + 60, comm) neighbors["W"] >=0 && MPI.Isend(u[xs[mep1]:xe[mep1], ys[mep1]], neighbors["W"], me + 70, comm) #receive if (neighbors["N"] >= 0) recv["N"] = Array{Float64,1}(undef, ycell) is_receiving["N"] = true rreq["N"] = MPI.Irecv!(recv["N"], neighbors["N"], neighbors["N"] + 50, comm) end if (neighbors["S"] >= 0) recv["S"] = Array{Float64,1}(undef, ycell) is_receiving["S"] = true rreq["S"] = MPI.Irecv!(recv["S"], neighbors["S"], neighbors["S"] + 40, comm) end if (neighbors["E"] >= 0) recv["E"] = Array{Float64,1}(undef, xcell) is_receiving["E"] = true rreq["E"] = MPI.Irecv!(recv["E"], neighbors["E"], neighbors["E"] + 70, comm) end if (neighbors["W"] >= 0) recv["W"] = Array{Float64,1}(undef, xcell) is_receiving["W"] = true rreq["W"] = MPI.Irecv!(recv["W"], neighbors["W"], neighbors["W"] + 60, comm) end MPI.Waitall!([rreq[k] for k in keys(rreq)]) for (k, v) in is_receiving if v u[ghost_boundaries[k][1], ghost_boundaries[k][2]] = recv[k] end end end 

5. Visualização da solução

O domínio é inicializado com um valor constante u = +10 ao redor do limite, que pode ser interpretado como a presença de uma fonte de temperatura constante no limite. A condição inicial u = −10 dentro da região (Fig. 6 à esquerda). Com o tempo, o valor u = 10 no limite difunde-se para o centro da região. Por exemplo, na etapa j = 15203 solução se parece com a mostrada na Fig. 6 à direita.

Com o aumento do tempo t, a solução se torna cada vez mais homogênea, enquanto, teoricamente, para $$$t \ rightarrow + \ infty$não se tornará u = +10 todo o domínio.

Fig. 6. A condição inicial (esquerda) e a solução na etapa 15203 no tempo (direita). Os limites da região são sempre armazenados em u = +10. Com o tempo, a solução se torna cada vez mais uniforme e tende a se aproximar cada vez mais do valor u = +10 em toda a região.

6. Desempenho

Fiquei muito impressionado quando testei o desempenho da implementação Julia em comparação com Fortran e C: descobri que a implementação Julia é a mais rápida!

Antes de nos aprofundarmos na comparação, vejamos o desempenho MPI do próprio código Julia. A Figura 7 mostra a taxa de tempo de execução ao trabalhar com os processos 1 a 2 (CPU). Idealmente, você gostaria que esse número estivesse próximo de 2, ou seja, o trabalho com dois processadores deve ser duas vezes mais rápido que com um único processador. Em vez disso, observa-se que, para tamanhos de tarefas pequenas (uma grade de 128x128 células), o tempo de compilação e a sobrecarga de comunicação têm um impacto negativo no tempo de execução geral: a aceleração é menor que uma. A vantagem de usar vários processos se torna aparente apenas para tarefas maiores.

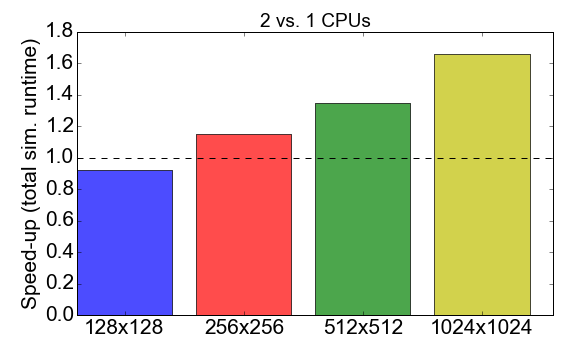
Figura 7. Acelerando a implementação do Julia MPI com dois processos versus um processo, dependendo da complexidade da tarefa (tamanho da grade). "Aceleração" refere-se à proporção do tempo total de execução usando 1 processo para 2 processos.

E agora uma virada inesperada: na fig. A Figura 8 mostra que a implementação de Julia é mais rápida que Fortran e C para tarefas de 256x256 e 512x512 (somente as que testei). Aqui, apenas medo o tempo necessário para concluir o loop de iteração principal. Eu acho que essa é uma comparação justa, pois para simulações demoradas essa será a maior contribuição para o tempo de execução geral.

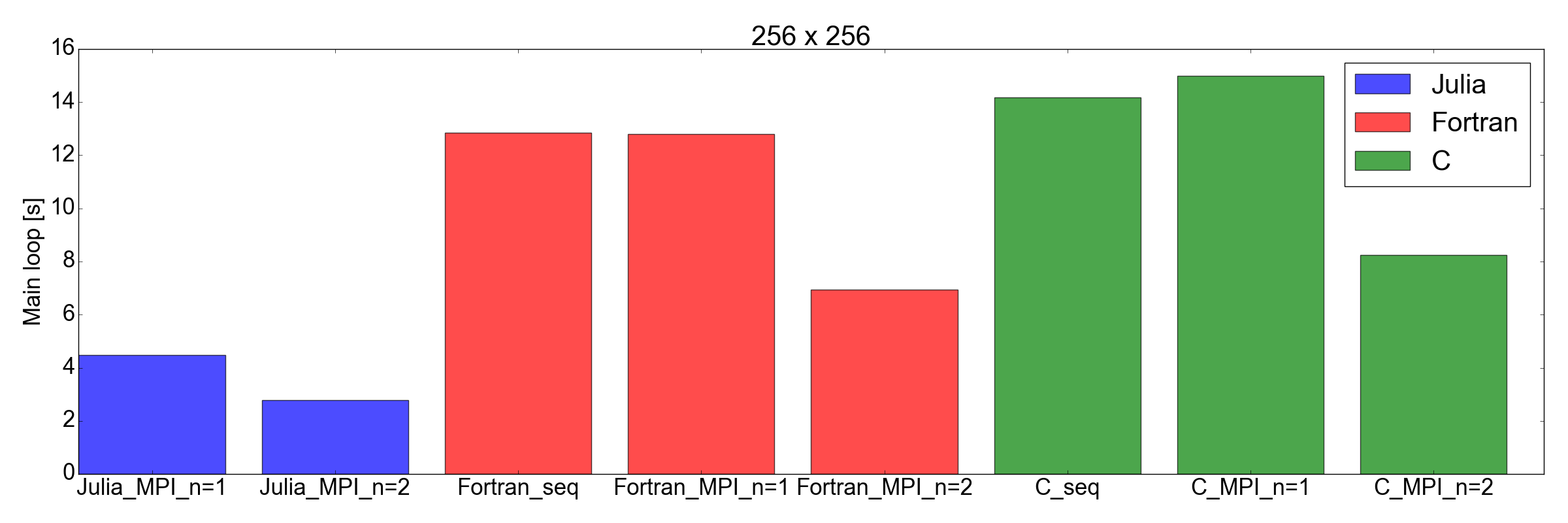
Figura 8. Desempenho de Julia vs. Fortran vs. C para dois tamanhos de grade: 256x256 (superior) e 512x512 (inferior). Isso mostra que Julia é a linguagem com melhor desempenho. O desempenho é medido como o tempo necessário para executar um número fixo de iterações no loop de código principal.

Conclusões

Antes de começar este post, eu estava cético em relação a que Julia pudesse competir com a velocidade de Fortran e C em aplicações científicas. O principal motivo foi que eu havia traduzido anteriormente o código acadêmico contendo cerca de 2.000 linhas de Fortran para Julia 0.6 e notei uma queda de desempenho de cerca de 3 vezes.

Mas desta vez ... estou muito impressionado. Na verdade, acabei de traduzir a implementação MPI existente escrita em Fortran e C para Julia 1.0. Os resultados mostrados na fig. 8, falam por si: Julia parece ser a mais rápida até à data. Observe que não levei em consideração o longo tempo de compilação consumido pelo compilador Julia, pois esse será um fator insignificante para aplicativos "reais" que requerem horas para serem concluídos.

Devo também acrescentar que meus testes, obviamente, não são tão abrangentes quanto deveriam para uma comparação completa. Na verdade, eu ficaria curioso para ver como o código funciona com mais de dois processadores (estou limitado ao meu laptop pessoal) e com outros equipamentos (consulte Diffusion.jl ).

De qualquer forma, este exercício me convenceu de que valeria a pena gastar mais tempo estudando e usando Julia para ciência de dados e aplicativos científicos. Vá para novas conquistas!

Referências

• Versão MPI do código de resolução numérica da equação de grau 2D
• Computação paralela
• Programação paralela com Julia usando MPI
• Programa Celeste